飞行模拟视景中森林建模技术研究

范曾，张建伟

（四川大学计算机学院，成都610065）

0 引言

几十年来，复杂植物的几何建模一直是计算机图形学面临的一个挑战。其中，真实、实时的树木建模与渲染是一个相当困难的部分。因为树木是户外场景的主要组成部分，并且具有复杂的拓扑结构和几何形状，需要大量的图元才能形成令人信服的视觉效果。树冠内树枝和树叶的重叠交错，以及树木在结构上的自相似性，使树木模型的生成变得复杂。

为了避免这些困难，此类三维模型的生成通常基于程序方法，如Lindenmayer 系统[1]，该系统通过形式语言的描述来创建模型，见图1。程序树模型在计算机图形学中很受欢迎，因为它们能够从一组输入参数生成各种输出树，并模拟植物与环境的交互，以便在虚拟场景中真实地放置树木。

不幸的是，要模拟特定的树或给定的树种，通常必须手动地调整许多参数。这使得建模的工作人员以及艺术家们背负着很大的创作负担。并且，大规模植物的几何复杂性仍然超过了当前计算机硬件的渲染能力。为了解决这个问题，研究者们已经开发了几种策略：①简化网格以减少多边形的数量；②用更基本的几何体（如点、线、圆柱体）替换复杂多边形；③用纹理或billboard 替换3D 几何体。这些方法都有效地提高了绘制大范围森林的效率。在飞行模拟机中，我们的树木模型是按照植物学规则构建的，它反映了植物的生长过程及其空间占有率。其中，树木的树枝由非常简单的圆柱体表示，足以用于沉浸式的视景视图中。

图1 Lindenmayer系统

1 相关工作

经典的树建模是基于规则或使用建模过程的。虽然Prusinkiewicz 和Lindenmayer 的L 系统[1]中的形式规则适用于初始状态，但大多数过程方法使用参数化算法，如Oppenheimer[2]、de Reffye[3]、Holton[4]、Weber 和Penn[5]。这些算法也对规则进行编码，但用的是更具体的概念。Lintermann 和Deussen[6]的xfrog 系统试图将这两种方法结合起来。

在经典的L 系统中，规则基础必须由用户编写。由于规则作用于局部，所以值的细微差异可能会导致整体形状的变化。这样的方式使得建模非常麻烦。从那时起，人们提出了L-系统的各种扩展，例如Prusinkiewicz 和Lindenmayer[7]的 参 数 化、Mech 和Prusinkiewicz[8]的开放式，和Prusinkiewicz 等人[9]的微分L 系统。这些扩展可以创建各种效果，但也会产生附加参数。Prusinkiewicz 等人[10]为L 系统提供了一个建模接口，以增强建模的简便性，但仍有大量参数需要用户定义。

程序性方法通常仅限于产生数量有限的形状。它们还可以限制用户可调参数的数量。然而，随着模型复杂性的增加，这个数量也会增加。虽然Oppenheimer[2]只使用了一些基本参数，但后来的方法，如Weber 和Penn[5]提出的方法有几十个参数。

在xfrog 系统中，使用一个简单的规则系统来组合过程元素，这样可以更快地进行建模。但是，参数的数量仍然很大。Ijiri 等人[11]使用基于植物学规则的交互式编辑器来创建植物模型。虽然这些编辑允许高效地制作花和叶序，但在制作复杂树木方面并不出彩。Okabe 等人[12]提出了一种基于草图创建树木的接口。在这种方法中，用户可以绘制树骨架的轮廓及其形状。然而，许多参数必须调整以达到特定的物种。

基于粒子的方法[13]在与自然生长相反的方向构造树骨架。最初，粒子是在树冠（球形或圆锥形）的树叶位置生成的。模拟流动的方法是，以小步重复移动粒子到其最近的邻居和根，当粒子非常接近时合并粒子。获得的粒子轨迹形成树骨架，随后用于挤出可渲染几何体。为了将粒子引导到地面，Rodkaew 等人使用静态目标点和最近邻吸引力，这会在粒子轨迹中产生急转弯，并严重限制建模的通用性。

粒子流算法对于从运动捕捉到的树枝尖端[14]或激光扫描[15]重建树也很有用。Xu 和Mold[16]提出了一种自顶向下的方法来构造不规则树模型。一个加权图是由一组随机生成的点在一个用户绘制的树shell 的旋转中构造的，其中一个点被指定为根节点，而其他节点的随机选择则指定端点。找到从各个端点到根节点的最短路径，并用于构造树骨架。此过程将重复多次，其端点来自上一次迭代服务的端点在下一次迭代中。这种方法比粒子流算法需要更多的内存，因为在每次迭代中都会构造出一个具有多个节点甚至更多边的新图。在他们使用引导向量的方法[17]的后期扩展中，作者使用了单个图，但是高空间复杂度仍然是该方法的主要限制。

Reche Martinez 等人[18]描述了一种非常精确但复杂的基于图像的建模方法。在这种方法中，使用一组注册的照片来确定给定树的体积形状。体积被分成单元块，对于每个单元块，用一组纹理计算出有效的视觉表示。完整的纹理集代表了树。然而，这种方式需要数十兆字节的纹理空间。另外，在不同的光照条件下也不容易显示树，因为光照已经包含在纹理中。

另一类不同的树木合成方法是资源竞争（如光、空气、水等）视为树木生长的驱动机制。其中提出基于局部生长条件的模型结构自组织生长是Pałubicki 等人[19]的关键贡献。

2 算法概述

本文的树木建模基于Pałubicki 等人的自组织建模方式，将树描述为一个分层组织的模块化结构。一片或多片叶子附着在茎上的那一点叫做节。茎在两个节之间的部分是节间。在每片叶的腋部形成一个侧芽，即支撑叶的茎和叶柄之间的有角空间。一个节间与附生的叶和芽形成一个变位异构体。

一个芽可能有四种不同的命运：产生一个新的变位异构体，产生一朵花，保持休眠（保持将来生长的可能性）或死亡。变位异构体可以连续或有周期地产生。温带气候树木的生长是有周期性的，受季节循环的调节。在一次生长（温带气候树木的春天）中产生的一系列变位异构体形成一个嫩芽。芽轴由位于芽端的顶芽产生。主干由幼苗的顶芽发育而来，轴序为0。轴序为n 的侧芽生长之后将会成为它产生的轴序+1 的顶芽。

生长方式分为两类：

（1）连年持续产生的嫩枝呈线性排列，形成单枝分枝结构。

（2）树木发育的主要推力转移到侧枝，顶芽产生一朵花或死亡。这样将会导致共轴分枝。新的分枝可以在同一季节产生（即与支撑它们的茎形成的同一季节）。

3 建模方式

通过模拟树木的生长过程，创建一个树形结构。

3.1 环境输入计算

本文将树木生长所需要的环境资源（如阳光、水分、空气等）用随机生成的3D 资源点表示。在程序运行之处，用C++的随机函数生成指定数量的3D 资源点。随后，将资源点构建为KD-Tree。我们假设每个芽被一个半径为r 的球形占据区所包围，并且每个芽有一个感知角度为θ、距离为R 的圆锥形感知体。在每一次生长迭代的过程中，根据构建的KD-Tree，从3D资源点集中删除任何芽的占用区域内的点，然后芽再去争夺剩余的资源点。用这种方式计算每个芽周围空间的可用性，同时依据空间定殖的方法计算芽的最佳生长方向。其中，若芽周围空间的可用性为0，则芽不生长；若芽周围空间的可用性为1，则芽可按照计算得出的最佳生长方向生长。

3.2 芽命运计算

在这个阶段，通过上一节中计算得到的芽周围空间的可用性决定芽的命运。由于目前尚不清楚自然界的根尖控制是通过资源竞争、激素控制还是二者都有，这里采用Pałubicki 等人实现的扩展模型进行资源分配。

该模型通过控制生长诱导资源向芽的分配来调节分枝，通过考虑分支点处（即芽）接收到的资源点数量分配纵向流动的资源。该算法氛围两个步骤：①到达芽的资源是流动的，累积值存储在节间。②累积值决定了该过程要分配的资源量：Resbase=αCbase，其中α是比例系数。到达分支点的资源按照公式（1）分布在连续的主轴Cm和横向分枝Cl之间。

其中，ε∈[0,1]控制资源是否偏向主轴（ε＞0.5），还是偏向侧枝（ε＜0.5）。到达一个芽的资源量Res 的整数部分决定了这个芽产生的变位异构体的数量：n=。

3.3 增加新芽

默认情况下，新幼芽是按芽所指的方向生长的。顶芽的方向与它的支撑节间的方向一致。侧芽的方向由叶序和芽与亲本节间的分枝角度决定。形成一个新芽的连续变位体的方向受到两个因素的影响：由环境决定的最佳生长方向和重力因素。因此，变位异构体的实际生长方向计算为上述三种方向的加权和。

随后，通过计算得出该芽在一次迭代生长之后的半径与长度，按照相应比例对替代树枝的圆柱体进行放缩，可得到新生长出来的树枝。

4 程序效果

该程序运行的界面效果如图2、3 所示。点击“Add Attr Pt Cloud”按钮生成随机的3D 资源点，绘制在窗口上，见图2。

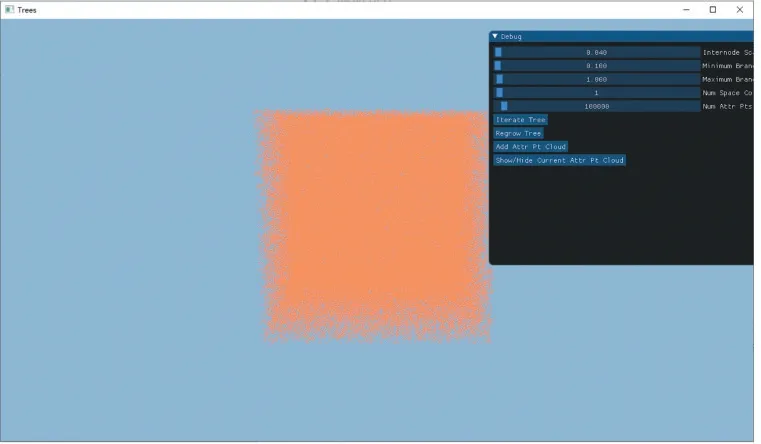
图2 随机资源点图示

随后设置不同参数（如树枝半径、迭代生长次数等），点击“Iterate Tree”按钮，每次点击树木会生长一次，如图3。

图3 动态生成树

5 结语

经过几十年的发展，森林的建模算法已经有了巨大的进步。本文通过研究最近30 年内树木的建模方式，对各种方式进行分析，结合飞行模拟视景的实际情况，基于自组织思想的建模方法，并利用OpenGL、Dear Imgui、glfw 以及glad 库编程实现了单颗树木建模的动态演示。该应用程序具备一定的可扩展性。然而，由于飞行模拟机这类大规模的视景需要在短时间内生成成千上万棵树，一个可行的优化改进方向是利用OpenGL 的Compute Shader 进行并行化处理。针对绘制效率的问题，还需要继续改进研究。