基于双轴超声列阵驻波原理的固体颗粒悬浮操控实验

朱琳琳,严雅琳,黎廷丰,唐小煜,蔡伟博,黎 铭

(华南师范大学a.物理与电信工程学院； b. 物理国家级实验教学示范中心，广东 广州 510006)

超声驻波悬浮技术是利用超声振动产生的辐射声压使悬浮体在没有任何附加效应的声场中悬浮或移动[1]，因其具有非接触，材料独立，不需要对小球预处理，可以悬浮固体、液体和气体等优点被广泛应用在物理、化学、生物、材料科学等领域. 目前，一维单轴式轴对称声悬浮器是目前应用最多的一种声悬浮装置[2]. 郭木铎[3]等建立单轴式声悬浮实验装置，实现对多层泡沫球的稳定悬浮，同时肯定凹球面反射面对于提高声悬浮器的悬浮能力的作用；范皓然[4]等基于超声相控阵构建复杂声场，通过调节发射反射面的几何参量，利用单轴式超声悬浮系统实现了样品的悬浮；朱怡[5]等基于单轴式声悬浮仪结构，通过调节超声波的频率和电压实现目标的静止到悬浮. 这类装置虽然能够实现悬浮物的悬浮，但产生的驻波声场比较弱，因而悬浮能力较小，其次不能使得悬浮物在谐振腔内移动，限制其使用与应用推广. 本文结合双轴超声列阵驻波机理，创新设计了平面-凹球面组合超声列阵悬浮模型，自主搭建了悬浮装置，实现了单粒子的束缚及定位移动，并测试了装置的稳定性.

1 声悬浮原理

1.1 超声波驻波

驻波是由频率和振动方向相同而传播方向相反的2列波叠加而成[6]，根据所发射超声波的波长，设超声波双发射端之间的距离为声波半波长的整数倍. 发射器两端所发射超声波波动方程分别为[5]

p1=p0cos (ωt-kz),

(1)

p2=p0cos (ωt+kz),

(2)

其中p0=ρ0c0u为无声扰时介质的压强. 所以叠加后的驻波声场声压分布为

p=pi+pr=2p0cos (kz)cos (ωt),

(3)

设z轴与两发射端声波的传播方向平行. 如图1所示，声压在z轴方向呈现周期性变化，波节之间距离为半波长的整数倍.

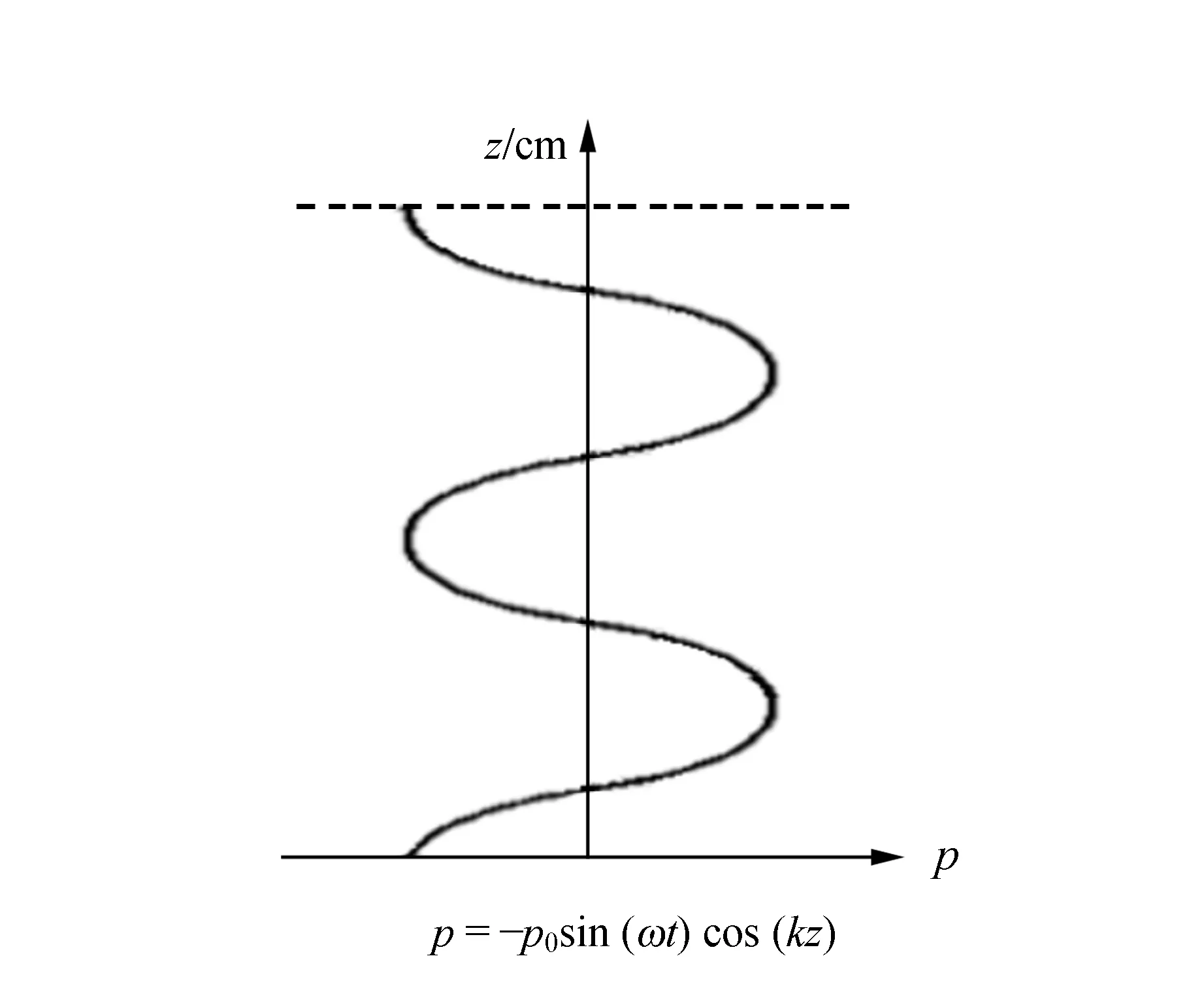
图1 驻波场中z轴传播的声压变化图

1.2 超声波换能器列阵

在实际的超声波悬浮实验中，若上下两端都是单个换能器的组合，源于仪器的功率问题，其所能提供的声辐射力不足，使得仪器很难浮起轻小物体，或者导致悬浮稳定性不佳. 为了得到更大的声场能量，将超声波换能器以某种特定的规律排列起来，形成超声波换能器列阵加强声场能量. 根据波的叠加原理，在某一方向上传播相同频率的多列超声波，会在空间中干涉，共同构建出能量更大的超声波声场[7]. 当仅有1对换能器发射超声波时，其声压在-1.5～1.5 Pa之间；而当有5对换能器发射超声波时，其空间声压可达-2.5～2.5 Pa.

若超声波列阵探头中每个晶片都独立，都有自己的接口、延时电路和A/D转换器，并且晶片之间彼此绝缘，那么此时超声波换能器列阵可作为超声波相控阵. 目前的超声波换能器列阵主要分为平面列阵和凹面列阵，二者都有聚焦干涉的作用，但因为凹面列阵具有自聚焦性，其聚焦性能要优于平面列阵. 为了简化装置，本实验将列阵中所有换能器并联起来以便统一操控.

1.3 声悬浮原理

根据Gor’Kov的声悬浮理论，从动量交换的角度分析，该理论认为声场中声辐射力的大小等于介质质点在悬浮小球表面这一封闭面上的动量变化率，所以在超声波驻波悬浮中引入声辐射力的时间平均势的概念[8]，Gor’Kov的理论指出，在悬浮小球半径远小于悬浮声场内的声波波长时，悬浮小球所受声辐射力的时间平均势的表达式为[2]

(4)

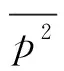
(5)

(6)

根据(6)式即可通过悬浮空间中的声场分布测量相应的质点振速，在已知流体介质静密度ρ0及声波在静止介质中的传播速度c0的前提下，可通过(4)式和(6)式计算出不同半径的悬浮小球在空间声场中所受声辐射力的时间平均势U. 当然为表述方便，一般用相对时间平均势：

(7)

代替时间平均势. 根据势能与力的关系，易得：

F=-U.

(8)

根据(8)式，可计算出半径为R的小球在c0和ρ0一定时，在声场中所受z方向上的声辐射力为

(9)

由于此声辐射力的方向沿着z轴方向，故在重力场作用下，声辐射力在某些位置可以抵消重力，创建局部的悬浮区域，使得半径为的悬浮粒子可以悬浮在该区域内，且这一区域为超声波驻波场波节附近区域[3,9].

1.4 移动原理

超声波驻波场中波节的位置与超声波的相位有关，而波节位置又是悬浮区域的位置，所以可以通过控制超声波相位的方法，使得悬浮粒子随波节移动而移动. 如图2所示，运用数字电路设计出与超声波频率相同方波信号，占空比为50%，以此作为超声波列阵的相控信号.

为解决串行切换带来相位误差，实验采用了FPGA芯片，通过并行输出解决此问题. 在相控方面采取如图2所示的切换控制信号的方式. 通过FPGA开发板的时钟将内部信号分频为频率40 kHz，分别对上下2个换能器列阵输入2路相位相反的PWM信号，差分形成方波信号，通过软件编程命令方波信号按照指定规律移动. 然后控制信号经过H桥驱动电路放大接入超声换能器中，使之正常工作. 通过触发FPGA板上的命令按钮，控制相位变化，使换能器发出相位变化的信号，从而使悬浮目标移动[8].

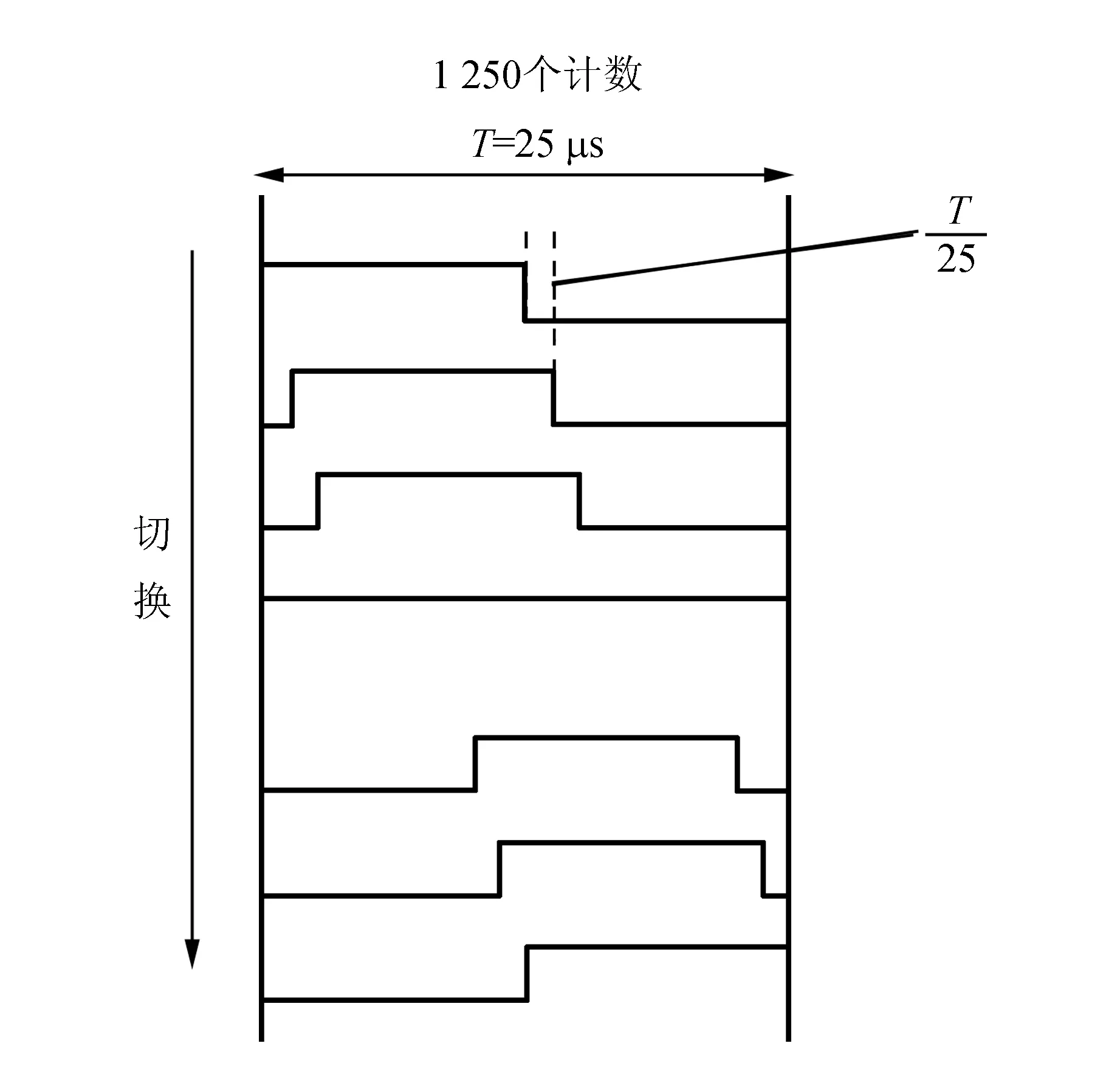
图2 控制信号相位变化图

2 实验装置

自主搭建了双轴超声列阵驻波原理的固体颗粒悬浮操控实验平台，图3(a)为利用COMSOL Multiphysics软件建模而成的3D装置图，图3(b)为装置的实物图. 实验平台主要由底座、超声发生电源、控制模块、悬浮装置部分等构成. 其中底座由木块和金属板组成，底座的镂空设计便于放置移动电池；超声发生电源可用7.2 V的移动电源或者实验室可调稳压电源，根据实验条件选择合适的供电设备，通过导线与控制模块相连；控制模块集成设计成3层板，通过在FPGA产生PWM信号，差分后形成方波控制信号，再通过驱动电路放大后，驱动悬浮部分的超声波换能器；悬浮部分由上下左右各36个超声换能器振子分别固定在凹球面-平面上，并用导线相互连接形成回路，通过控制模块驱动，产生40 kHz超声波，使上下左右的超声阵列振动，从而形成驻波声场，实现颗粒的悬浮与操控.

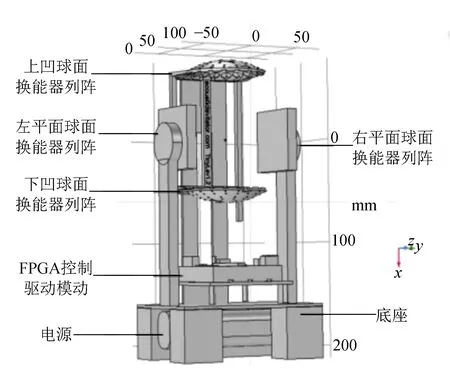
(a)装置3D建模图

在本文的所有实验中，皆是采用直径约为1.5 mm，密度为0.91 g/cm3的聚苯乙烯泡沫塑料小球作为悬浮目标，采用的超声换能器振子型号是响应频率为(40.0±1.0) kHz，输入峰值电压为40 V的NU40C10T-2开放型. 利用外部电源供电，通过按键控制FPGA模块产生控制信号，经过驱动电路作用于平面-凹球面换能器列阵. 装置系统框图如图4所示.

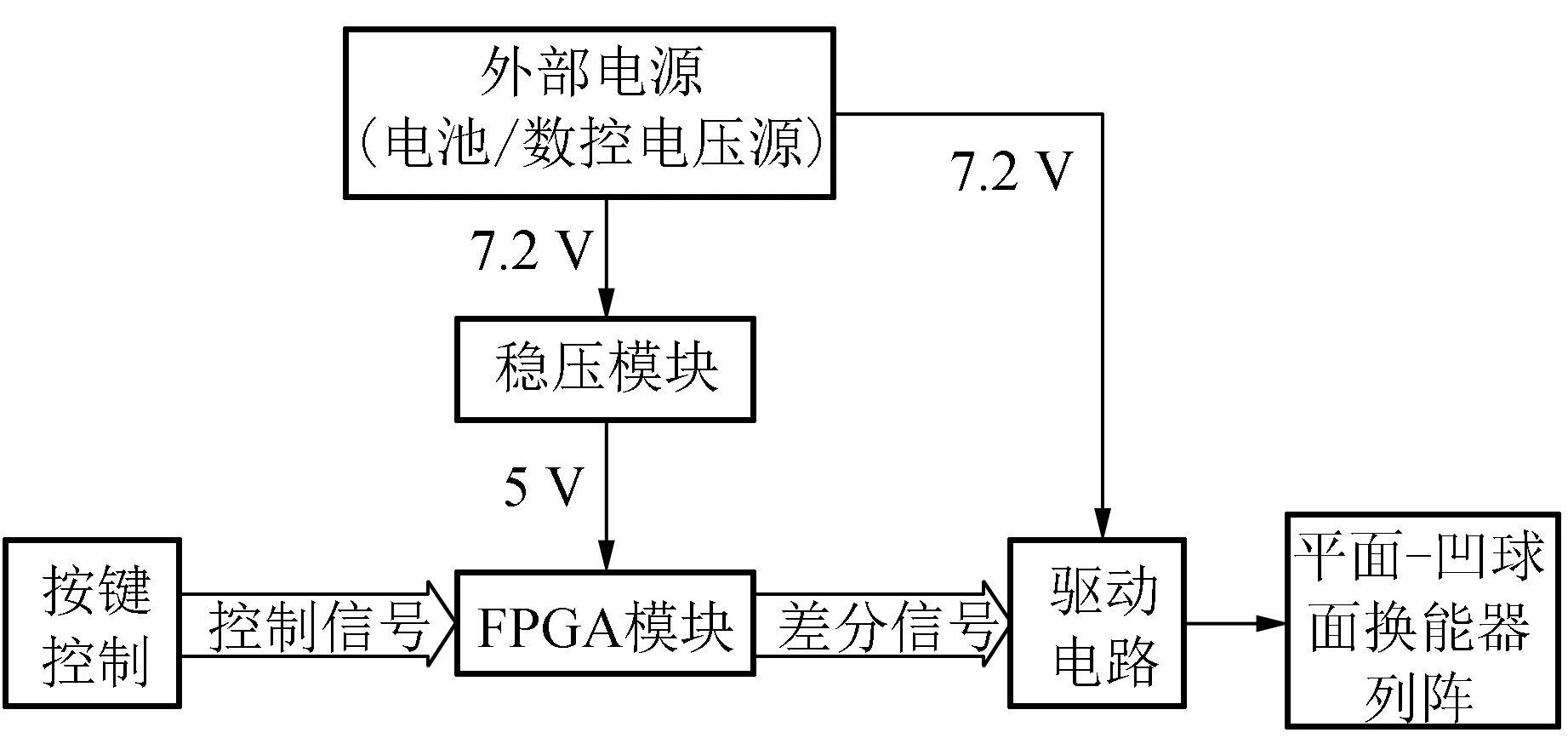
图4 装置系统框图

3 实验过程与数据分析

3.1 实验仿真

在正式实验开始之前，采用COMSOL Multiphysics模拟软件进行仿真预实验，模拟凹球面列阵与平面列阵组合的双轴悬浮声场分布，如图5所示. 从理论上证实列阵组合的可行性. 设置凹球面部分和双边平面部分发射40 000 Hz的球面波，其他部分的边界区域则设置为开放边界条件，由仿真结果得，仿真图中心区域的淡橙色部分为声压节点位置，即粒子悬浮区域. 对比平面-平面组合，凹球面和平面列阵组成的双轴悬浮装置所产生的声场也出现“网格”状的声场分布，对比单轴凹球面的悬浮装置，此组合模型聚焦性性能更强，旁瓣较少，容易实现粒子的悬浮和定位操控. 对比双轴凹球面-凹球面的悬浮装置，虽然声场的聚焦性更强，但是过强的聚焦性难以实现对粒子的定位移动操控. 因此凹球面-平面列阵组合的双轴悬浮模型是可行的.

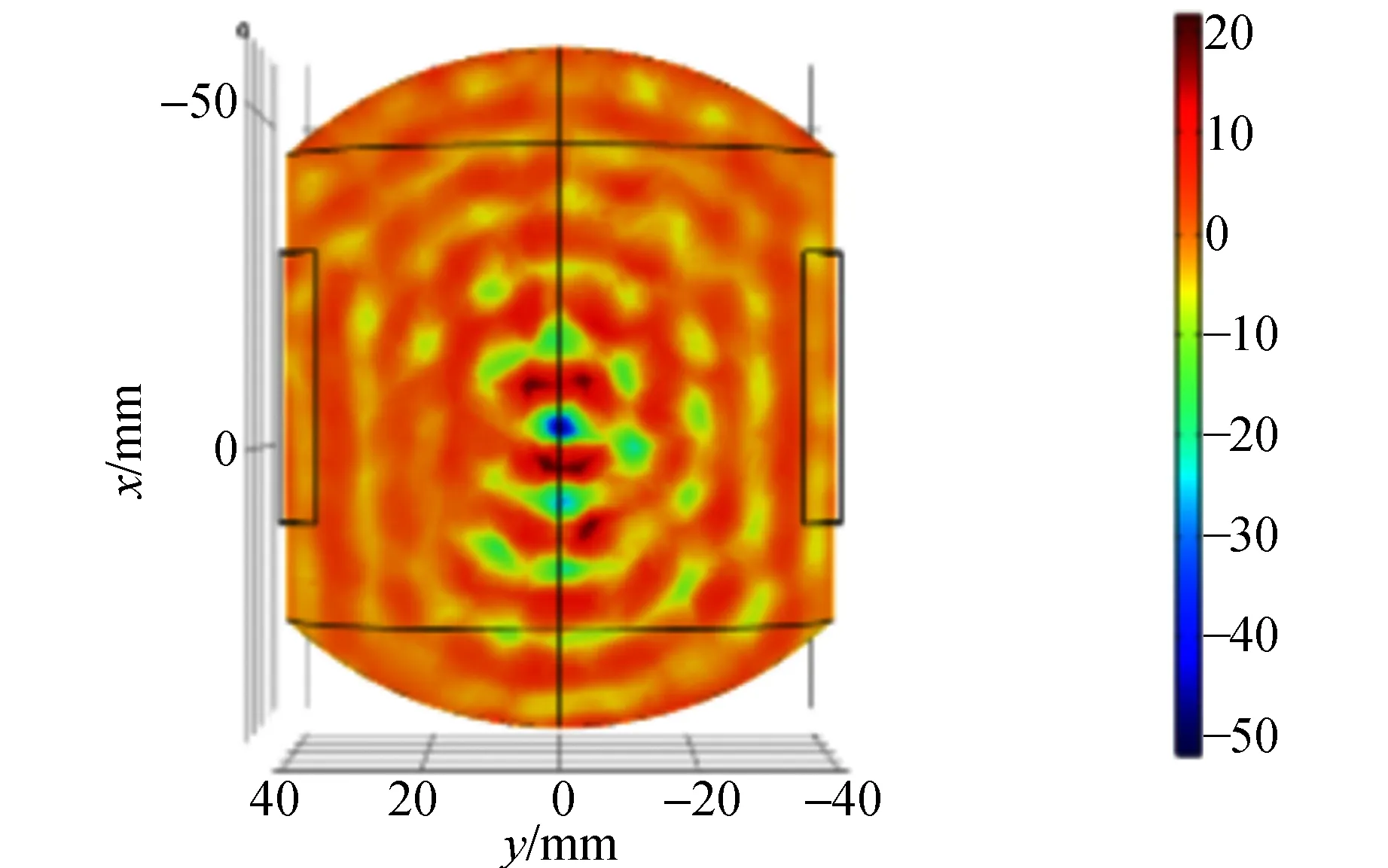
图5 模拟驻波场声压分布图

3.2 单粒子的悬浮

利用设计的实验装置实现悬浮目标的稳定悬浮. 将悬浮粒子送入装置内进行悬浮，待稳定悬浮，记录悬浮目标的位置，重复多次实验，同时对实验全程进行录制，实验后将视频导入Tracker软件，分析得到悬浮目标的悬浮位置(图6). 为了探究悬浮目标悬浮的准确程度，将实际悬浮实验中悬浮目标的悬浮高度与仿真实验中声压节点高度(图7)进行对比，计算其相对偏差，得到数据如表1所示.

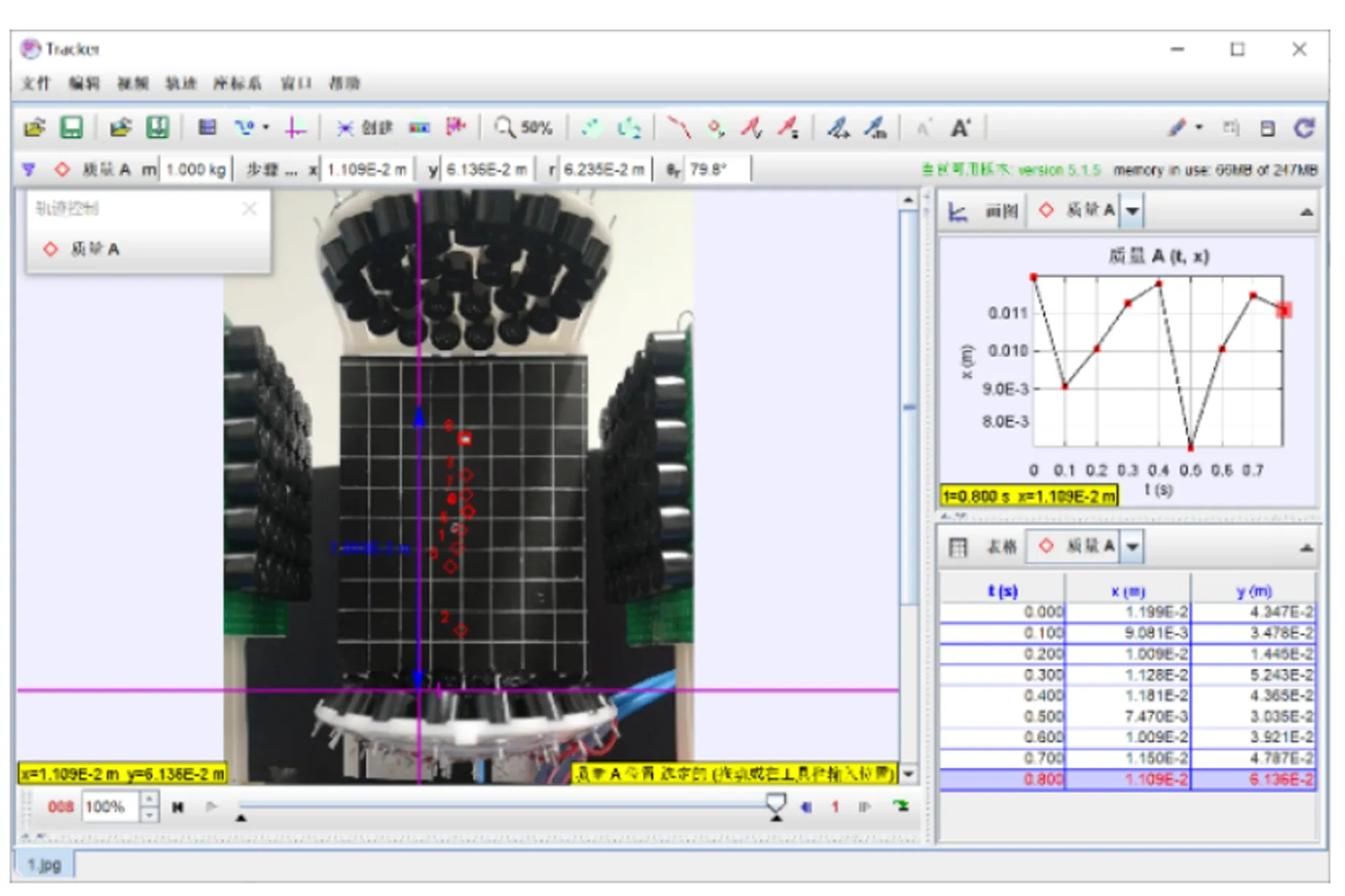
图6 使用Tracker软件对悬浮粒子进行定位

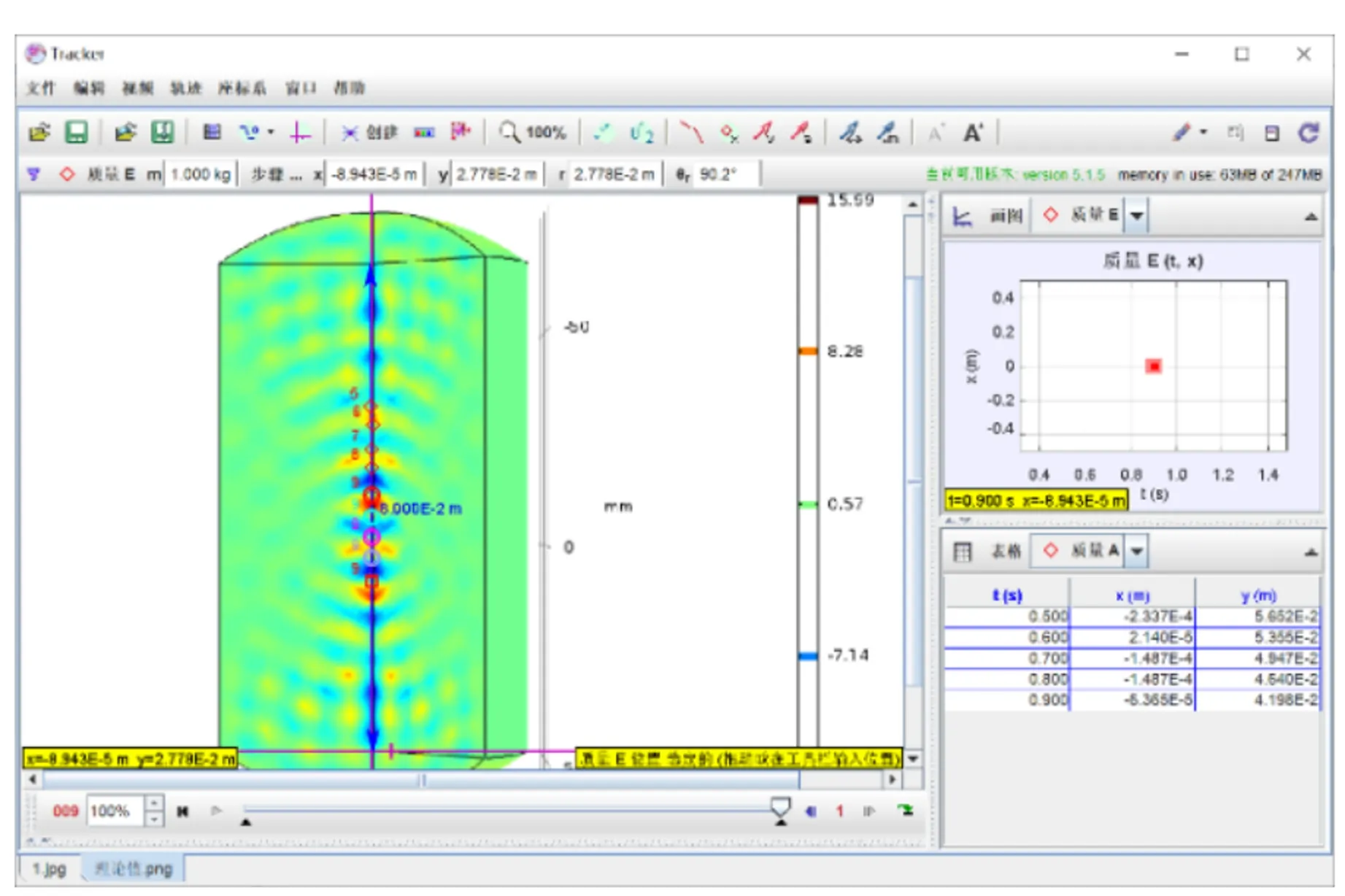
图7 使用Tracker软件对仿真模型中声压节点进行定位

从表1可以看出，实际悬浮实验中悬浮目标的悬浮位置与仿真实验吻合度较高，相对偏差较小，多次实验平均相对偏差为Er=1.67%. 因此实验装置的实际悬浮高度与理论的悬浮高度匹配度较高.

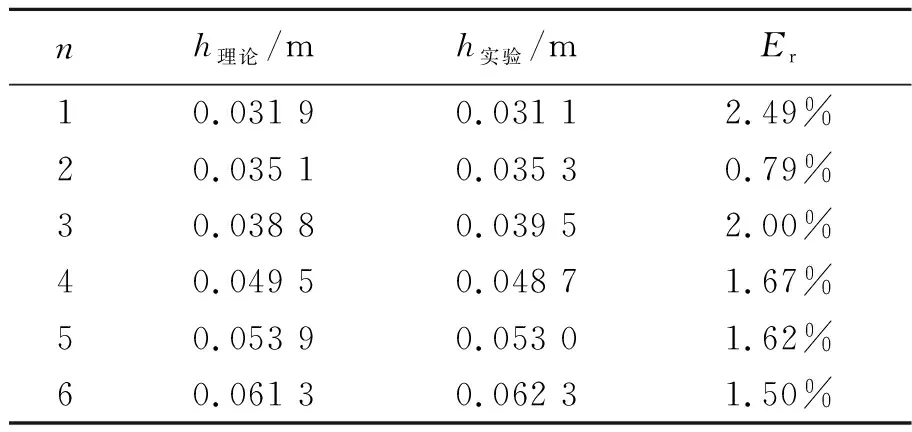
表1 仿真得到的声压节点位置与实际悬浮位置对比

3.3 单粒子的操控

超声列阵结构具有较强的悬浮能力和移动能力，尤其是凹球面超声列阵的悬浮能力由于曲面聚焦效应而大大增强[8]. 基于超声列阵悬浮的基础，超声列阵能够实现悬浮目标的稳定悬浮，但是仍存在不足之处. 不论是李文斌[7]等设计搭建的开放式阵列悬浮试验平台，还是王英伟[8]等设计搭建的凹球面阵列超声悬浮系统，或者是武二永[10]等搭建的基于换能器列阵的超声悬浮实验装置，尚未实现对悬浮目标的二维、三维移动以及定位操控. 因此，本文以此为研究焦点，探究在超声列阵悬浮的基础上实现对粒子的二维移动，从而定向操控粒子的运动情况.

基于本文设计搭建的平面-凹球面列阵，进行单粒子悬浮定位操控的实验操作. 首先将单粒子悬浮在装置中心偏下方位置，以便观察粒子在径向、轴向的运动情况，待粒子稳定后，观察控制板上的显示灯，若显示灯不亮，表示装置处于上下控制模式，按压控制板块上的按键，改变输入信号，实现悬浮目标的上下移动；按压控制板块的模式按键，切换控制模式，使得装置处于左右控制模式，此时按键控制并实现悬浮目标的左右移动.

由于平面-凹球面模型的特殊性，在阵元数量、圆环间距和凹球面半径等因素的多重影响下，导致声场呈现比理论仿真更为复杂的声场分布. 因此，在复杂的声场中并不能实现悬浮粒子的任意移动，经过多次实验，发现悬浮目标能够实现图8所示的移动.

(a)粒子原位置

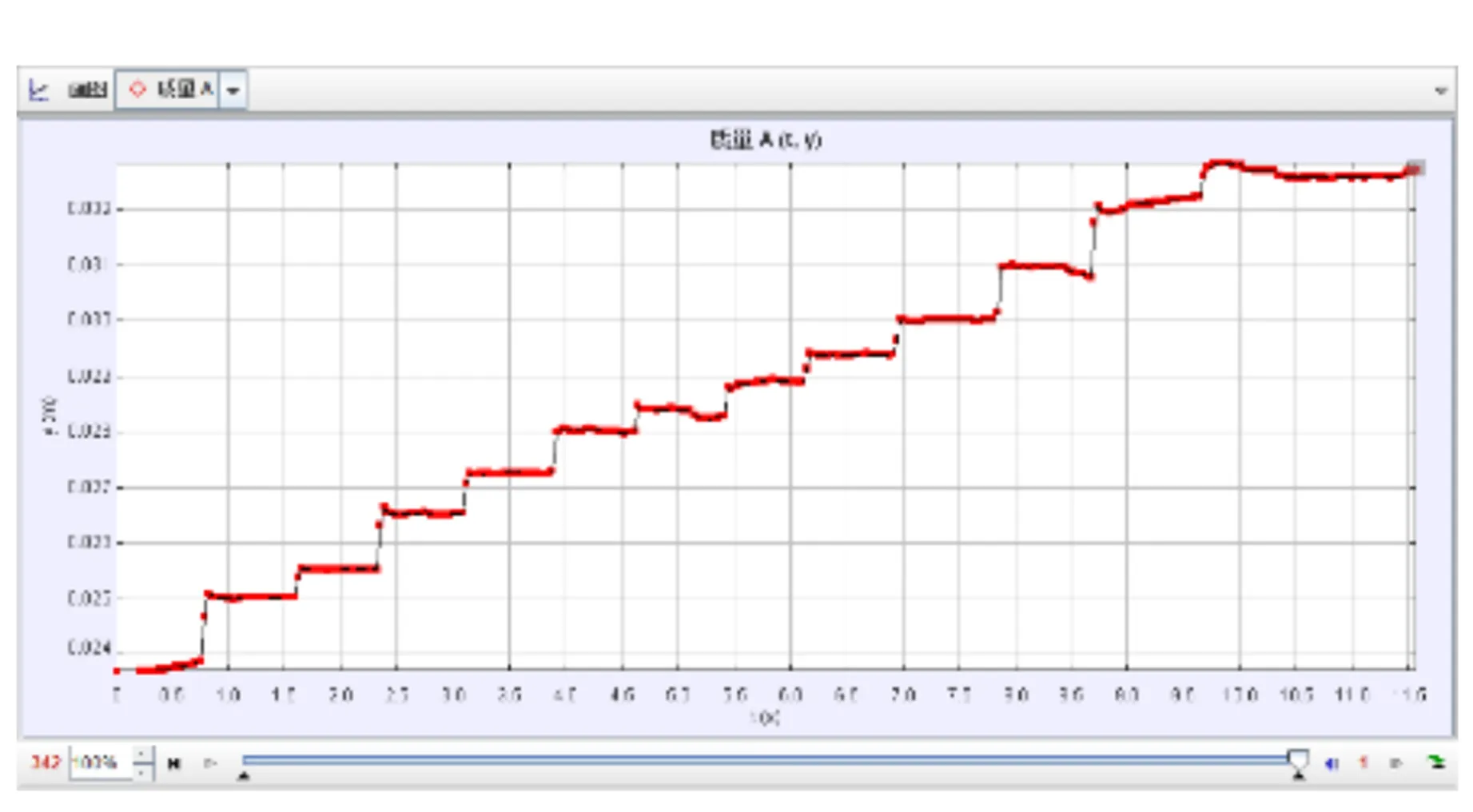
在单粒子的定位移动操控中，每次触发相位改变按键，悬浮目标都将进行一定的位移，但是对于粒子操控的准确性并未有较为数据化的体现. 因此为检验粒子操控的准确性，以上下移动为例，仅让悬浮粒子在竖直方向上移动(图9). 将视频导入Tracker软件，分析计算出每12步长(1个周期)悬浮小球走过的距离，并与理论值进行对比，如图10和表2所示.

图9 操纵粒子上下移动

(a)向上运动

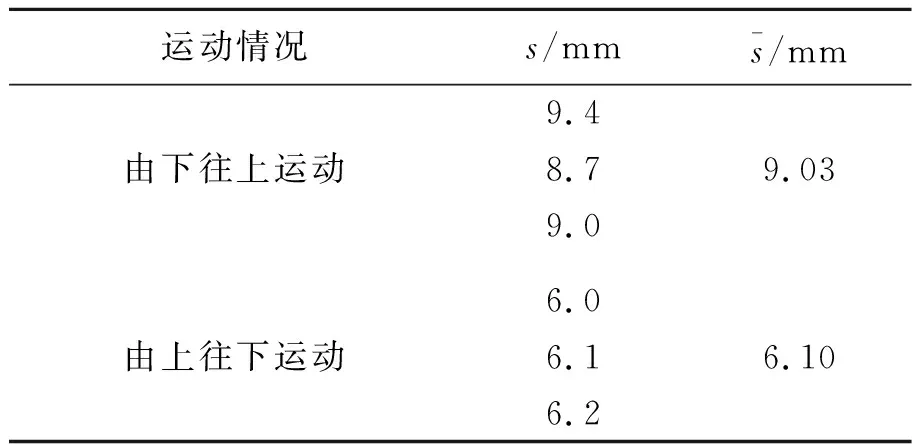
表2 悬浮粒子在竖直方向的移动距离

在移动过程中，相位变化会使粒子出现逃离原来的波节，被吸引到新波节的情况. 纵使对悬浮目标的操控的准确度存在一定的误差，但是在超声列阵悬浮系统中实现对悬浮目标的移动与定位也是研究的一大进步.

3.4 稳定性实验

评价悬浮装置的稳定性如何，可通过对悬浮物的稳定悬浮时间来进行初步验证[11]. 无论是解文军[12]等研制的磁致伸缩式单轴超声悬浮装置，还是江海[11]等设计的超声驻波悬浮装置均能实现超过30 min的稳定悬浮，而在实验中本装置也能实现超过30 min的稳定悬浮，因此采用悬浮时间作为悬浮物稳定性方案的判断并不全面，参考朱怡[5]等利用转动平台以及倾斜轨道验证整体装置的稳定性.

借助智能小车，带动整体装置分别做180,380,560 mm/s匀速运动，并以双摄像头形式分别拍摄远景和近景视频(为方便观测，将两侧的平面列阵拆下)，将视频导入Tracker软件，分析装置随小车的运动情况.

远景视频分析悬浮目标在水平方向的运动轨迹，近景视频分析悬浮目标在平衡目标附近的轻微扰动程度. 虽然悬浮目标会因为装置的运动产生偏离平衡位置的轻微扰动，但从图11和表3总体看，3个速度的抖动方差差距不大，说明整体装置较为稳定.

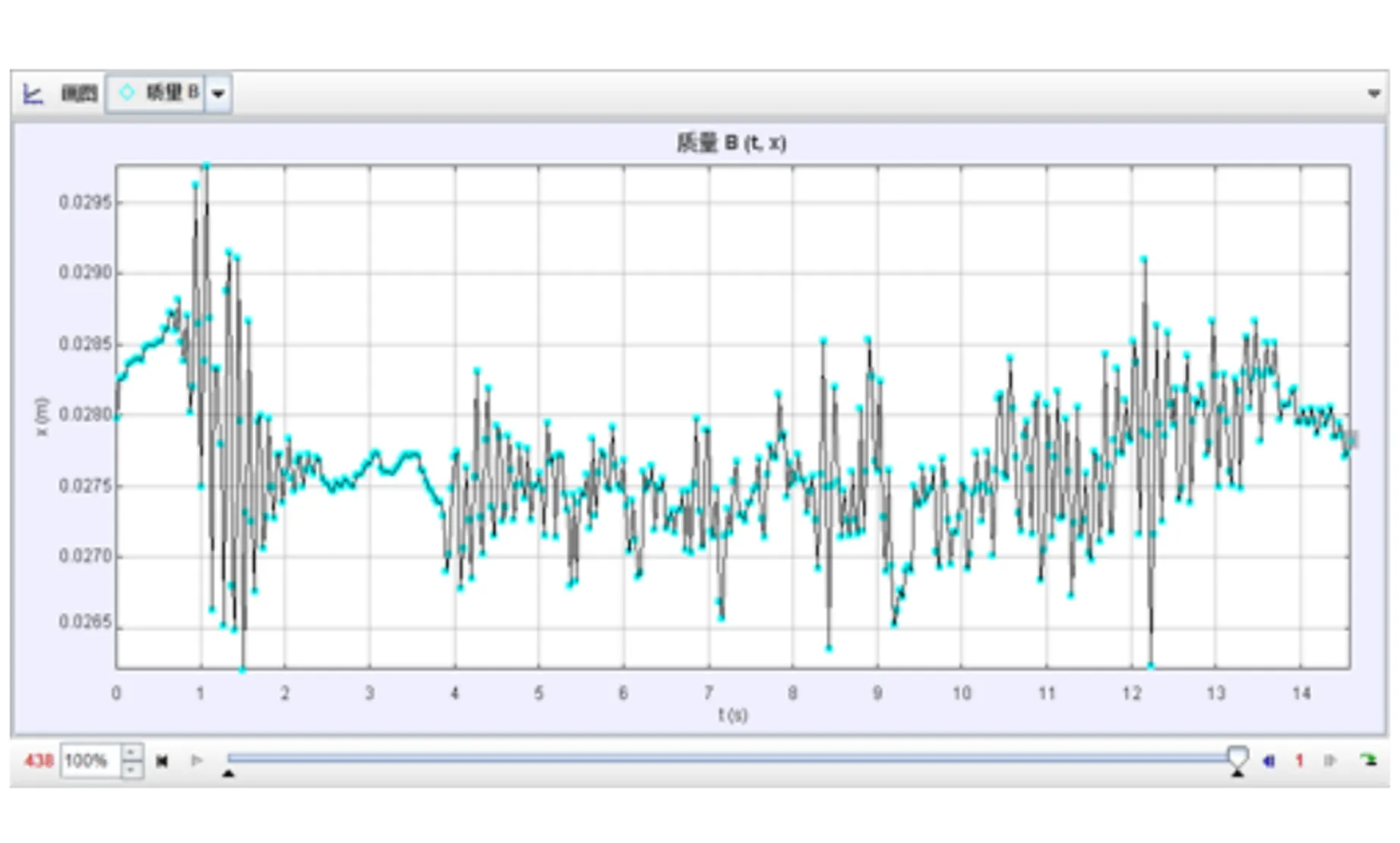
(a)180 mm/s

表3 装置不同速度运动中悬浮粒子悬浮抖动情况

实验中发现若装置能够在起始至达到匀速过程中保持稳定，则在匀速状态中均能保持稳定悬浮，为了深入探究悬浮目标脱离装置的临界情况，遥控智能小车加速运动，使用手机传感器Phyphox软件加速度传感器模块[13]实时记录实验中加速度大小(图12)，测得装置在加速度为3.0～7.5 m/s2时，悬浮目标脱离装置.

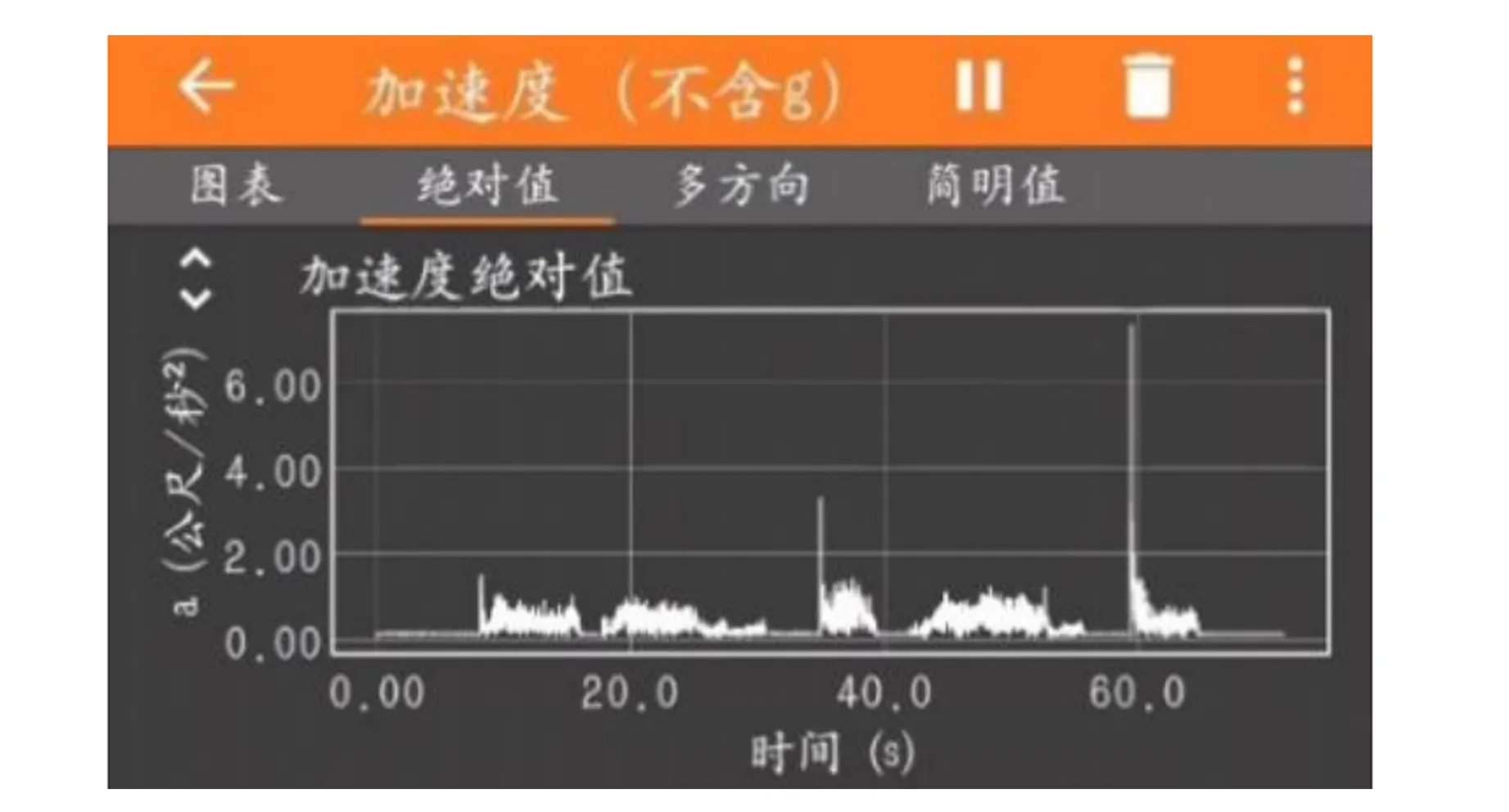
图12 Phyphox软件测量得到装置运动加速度

4 结 论

为了利用超声阵列结构实现固体颗粒的悬浮操控装置，设计了平面-凹球面的双轴发射极的超声列阵. 通过预实验仿真软件优化设计，确定了平面-凹球面的双轴悬浮模型的理论可行性，并搭建了超声列阵悬浮实验装置. 在装置中实现了单粒子的稳定悬浮，其中悬浮粒子与仿真理论值对比，平均相对偏差为1.67%；在悬浮的基础上，还实现了对单粒子的定位移动操控，不仅实现了悬浮粒子的径向移动，同时也实现了悬浮粒子的轴向移动，并以竖直移动为例探究粒子移动的准确度，得出悬浮粒子从上到下运动的相对偏差为1.6%，从下到上运动的相对偏差为2.2%. 最后，通过装置在运动过程中水平方向的直线轨迹偏离情况以及在平衡位置附近的轻微扰动程度表征悬浮目标的稳定性[14]情况. 实验表明，当运动加速度为3.0～7.5 m/s2时，悬浮目标脱离装置.