基于BP神经网络的横流式蒸发冷凝器鼓泡式板片传热性能预测*

上海理工大学 上海市动力工程多相流动与传热重点实验室 席鹏飞 章立新 张坤龙 陈 权 周庆权 高 明 刘婧楠 陈永保

浙江三新科技有限公司 潘旭光 陈婷婷

0 引言

板式蒸发冷凝器在制冷过程中的工作原理是将板内高温气态制冷剂的冷凝热传递到板外表面的水膜中，水膜与空气间再通过对流的显热传递和蒸发的潜热传递最终将热量散发到大气中。

在蒸发冷凝器中，有工质与壁面间对流与凝结换热、壁面热传导、水膜与壁面对流换热、水膜热传导、水膜与空气的显热与潜热交换这一系列换热环节，在这些环节中，蒸发侧(即水-空气侧)的热阻一般最大，因此强化传热的重点在于水-空气侧传热的优化。与平直板片相比，凸凹结构的板片增强了扰流，破坏了边界层，同时增大了换热面积。鼓泡式板片通道类似于长方形狭窄通道，通常通道内的流动处于低雷诺数湍流状态。目前关于鼓泡式板片几何参数对板片通道内流动与传热的影响规律有一些研究。王定标等人提出蜂窝板的传热性能优于平板，用数值模拟的方法研究了雷诺数、倾斜角度对换热性能的影响，并从场协同的角度分析了凹凸板换热强化的原理[1-2]。张延丰等人基于多场协同原理进行了数值模拟，得出了鼓泡式板片传热元件的几何参数对流动与传热的影响规律和优化措施[3]。Samad等人[4]、王光辉等人[5]分析了凹坑凸包的直径、深度等几何因素对板片的传热和阻力性能的影响。简弃非等人分析了凸凹板在横流蒸发冷凝器水-空气侧的传热传质机理，并归纳了散热量、进风状态、冷却水温度等对系统能效比的影响[6]。

上述研究主要针对板片本身的几何参数，本文针对横流式蒸发冷凝器中特定几何参数的鼓泡式板片的蒸发侧传热规律，在不同板片间距、不同水膜流量、不同截面风速下，通过一定量实验测出复合换热系数。但因环境条件不可控，实验的环境参数随机，为总结和研究其传热规律，采用BP神经网络进行处理，以得到实验范围内其他参数条件下复合传热系数的预测值。

BP神经网络能够在输入输出的数学模型未知的情况下，通过反向传播进行参数学习，以此寻找网络误差最小化的参数组合[7]。在BP神经网络的应用上，孙金颖等人分析了建筑节能改造案例，并确定了关键影响因素，通过使用BP神经网络对现有的建筑节能改造评价体系建模，从而提出了新的适合我国国情的建筑节能改造模式[8]；李祥立等人以大连某建筑为测试对象，使用BP神经网络对其地板供暖系统的热负荷建模，在实际测量的供暖期不同时段的热负荷数据基础上，进行了预测研究，结果表明，神经网络预测模型能够准确预测一个单元未来24 h不同时段的热负荷，预测误差约为5%[9]。从这些学者的研究中可以发现，在工程实例中使用BP神经网络进行预测是完全可行的，并且其预测精度满足了使用需求。因此，用BP神经网络预测鼓泡式板片的性能是可行的。

本文搭建了鼓泡式板片用于横流式蒸发冷凝器时蒸发侧传热性能测试实验系统，对鼓泡式板片在不同工况下的传热性能进行测试，并建立了3层BP神经网络(输入层、隐含层和输出层)对复合换热系数进行预测。输入层由5个参数组成，分别为进口空气干球温度和湿球温度、喷淋水流量、截面风速、板片间距，输出层为复合换热系数。

1 实验台及部件

实验系统的主要部件包括带电加热的鼓泡式板片、可变频的风机、喷淋水泵及相应的风道和水管路，调节设备包括用于风机的变频器、用于电加热的调压器、用于水路的流量调节阀，测量设备包括大气压力计、干湿球温度计、转轮风速仪、浮子流量计和热电偶等。图1为实验台布置实物图，图2为流程简图。图3a为鼓泡式板片的表面实物图，鼓泡式板片高740 mm，宽240 mm，材料为碳钢，加工前的基板厚2 mm，凸包高2 mm、直径10 mm，凸包布置如图3b所示。热源为埋于板片内的电加热线，冷源为环境空气。所测的鼓泡式板片试件主要由鼓泡板、导热泥、电加热线、保温材料、背板组成，如图4所示。因鼓泡式板片材质的导热系数大且壁薄，可忽略板材的传导热阻，以板内侧壁温代表板的表面温度，故在板的内侧壁上均匀布置16个铜-康铜热电偶，热电偶线直径为0.3 mm，其热端与板的内侧壁紧贴，用导热泥压紧，冷端置于冰水混合物中。在导热泥中埋入电加热线，导热泥可起均匀温度作用，导热泥后覆盖绝热板，并在背板与鼓泡板的接缝间加密封垫后通过螺栓连接，压实导热泥、电加热线、绝热板，并保证试件不漏水。在背板内侧(即背板与绝热板间)也布置了一对热电偶，以监测其是否漏热。2个相同的鼓泡式板片试件对置，构成蒸发冷凝器的蒸发侧通道，通道结构的特征为板片的凸点对凸点、凹点对凹点，且板片间距可调。每个试件的上沿各有一个蓄水槽，长度与板片宽度相等，蓄水槽内的纱布引导喷淋水自上而下流出，即每侧板片上的水膜流量是喷淋水管路上浮子流量计读数的一半，本文计算所用流量是两侧板片上的总流量。板片间距D为凹点的间距(即流道最大间距，因为板片压制时，四周法兰面与凹点平齐)，而截面风速则取板片间截面的平均风速(即计算风道横截面时取两板片凹点与凸点中位面间的距离D0，并忽略水膜厚度)。D和D0见图4。

图1 实验台布置

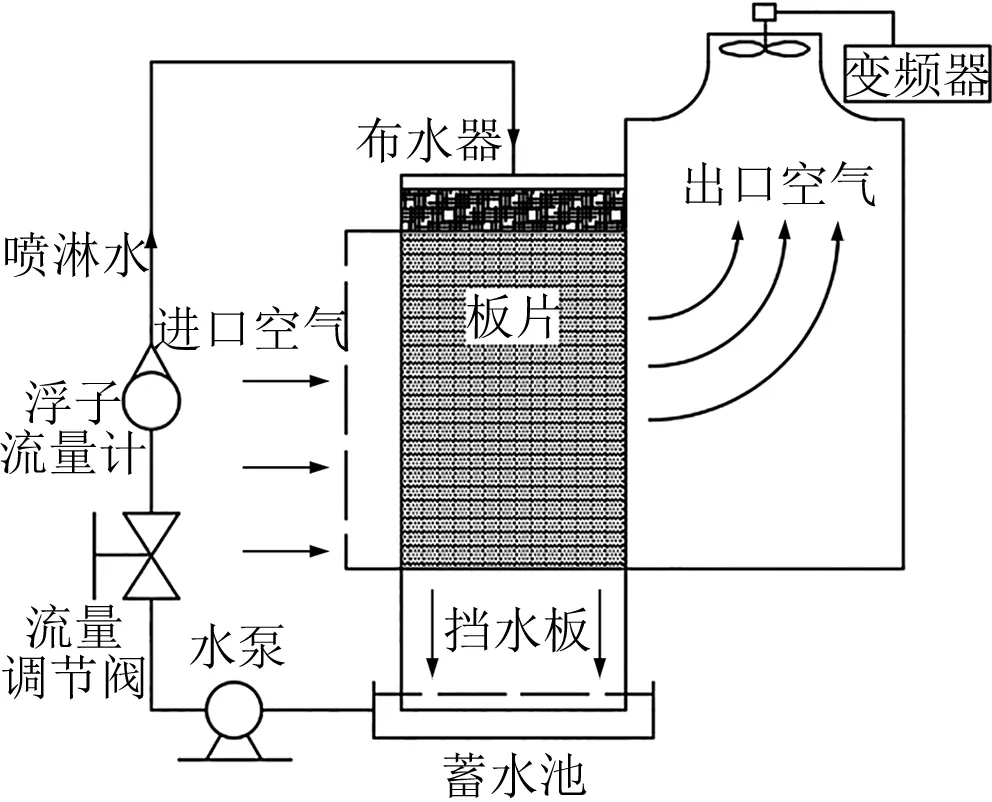
图2 实验台流程简图

图3 鼓泡式板片

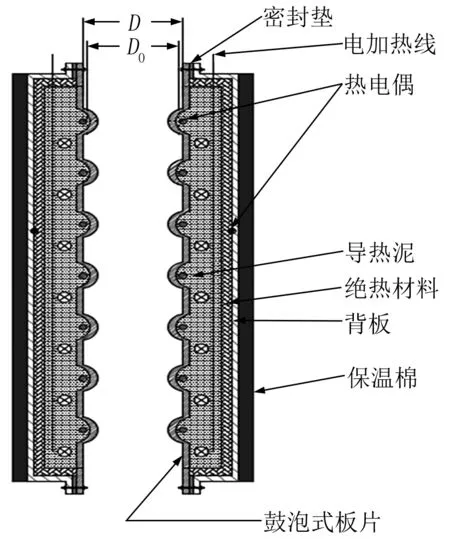
图4 试件结构示意图

实验台运行时，由喷淋水泵将喷淋水从水池输送至试件顶部的布水器，布水器将水均匀布洒在鼓泡式板片上沿，并沿板片表面形成一层薄水膜，水膜因重力向下流动，最后沿板片的下边沿流到水池中。空气在风机作用下，从板片试件一侧竖边流入，与喷淋水直接接触并呈横向交叉流动，然后从另一侧竖边流出，经过风量测试段后从风机排出。风量测试段位于风机下方，为一矩形腔，设有3个风速测点，根据所测风速的平均值和该矩形腔截面积可算出风量，从而换算得出板片通道的截面风速。

待水、气运行稳定后，调节电加热功率，使板片温度保持为60 ℃，实验中板片上热电偶的温度基本一致，证明板片壁温分布均匀，本文所做的试件采用电加热模拟冷凝放热是成功的。大气压力由空盒气压计测得，进出口空气干湿球温度分别由铂电阻温度计、湿球温度计测得。

2个板片壁面上分别均匀设置了16个热电偶温度测点，以热电偶所测温度的平均值作为板片温度；板片外壳与保温棉间设置了2个热电偶，测量外壳温度，以计算外壳散热热损失；因难以准确测量板片表面喷淋水膜的温度分布，在板片上的蓄水槽和板片下端的出水部位各设置了1个热电偶来测温，分别视为喷淋水的进口和出口温度；进、出口空气的干、湿球温度由干湿球温度计测得。以上数据的采集方式均为每分钟采集60组数据并取其平均值记录。

实验中采集样本数据的范围见表1。

表1 实验数据范围

空气带走的热量为

(1)

式中Qa为空气带走的热量，kW；Goa为出口空气的体积流量，m3/h；ρoa为出口空气的密度，kg/m3；hoa、hia分别为出口、进口空气的比焓，kJ/kg。

平均温差取板片温度与板片上喷淋水膜表面空气湿球温度的对数平均温差，也称为湿温差。设板片的平均温度为tw，空气进、出口的湿球温度分别为twbi、twbo，则定义

Δtmax=tw-twbi

(2)

Δtmin=tw-twbo

(3)

平均温差Δt可由下式计算得出：

(4)

系统内的主要传热环节有2个：

1) 电加热产生的热量通过换热板片传递给板片外侧的水膜。

2) 板片表面覆盖的水膜与空气的热质交换将热量传递到空气中。

待系统稳定运行后，进口水温等同于出口水温，因此可认为进出口空气的比焓差数值等于板片的散热量数值,用式(5)计算板片与空气间的复合换热系数K[10]：

(5)

式中A为板片单个表面的换热面积。

热平衡偏差β的计算式为

(6)

实验方案见表2。

表2 实验方案

实验系统循环稳定后，每分钟记录1次数据，每个工况共记录5组，调节喷淋水流量、风机频率、板片间距来改变工况，最终共获得175组测试数据。

2 网络建模

2.1 网络原理与参数设置

从结构来看，BP神经网络一般由3层组成，即输入层、隐含层和输出层。BP算法的学习过程有正向传播和反向传播2个过程：在正向传播过程中，从输入层开始到隐含层、输出层依次计算各层各节点的实际输入、输出，这个过程中，每一层的神经元只会被上一层的神经元所影响，所以也称为多层前馈阶段；若输出层不能取得期望值，则进入反向传播过程，即根据输出层神经元的输出误差，沿路反向修正各神经元之间的权重和阈值，从而使得输出值逼近期望值，所以也称为反向误差修正阶段。

按照隐含层的数量，BP神经网络可分为单隐含层网络和多隐含层网络。一般来说，单隐含层BP网络已经能够满足映射任何有理函数的需求，此外，虽然增加隐含层的层数可以使误差更小，提高精确度，但同时也会使网络复杂化，导致训练网络权值的时长大大延长；同时，增加隐含层神经元数量也可以提升预测精度，并且其训练结果比增加层数的方法更容易发现和调整[11-12]。因此，本文采用单个隐含层的BP神经网络，其结构如图5所示，而隐含层神经元的数量则由下文的计算择优选取。

图5 单个隐含层的BP神经网络结构示意图

K值的大小不仅与平均温差有关，还与喷淋水流量、截面风速、板片间距及进口空气的干球温度和换热区间的气压等相关。根据以往经验，在开放式系统中，气压影响较小，本文将该因素的影响忽略不计；作为蒸发式冷凝器，本文以60 ℃的冷凝温度为应用背景。输入层中选取了5个影响因素作为输入参数，分别以进塔空气干球温度ti、进口空气湿球温度twbi、喷淋水流量Q、板片间截面风速vair、板片间距D为输入值，复合换热系数K为输出值。图5中Wmnk代表第m层的第n个神经元到第(m+1)层的第k个神经元的连接权重，在迭代时会按式(7)沿梯度下降方向进行更正[13]：

(7)

式中η为学习效率，取值为0.1；E为目标网络中所有误差的平方和。

2.2 性能评价指标

使用相关系数R、平均相对误差MRE和均方根误差RMSE来评价预测模型的性能。相关系数R的范围为[0,1]，越接近1，参数间相关性越大。平均相对误差MRE、均方根误差RMSE的计算式分别为

(8)

(9)

式(8)、(9)中N为样本容量；ai为实际的输出值；pi为预测的输出值。

洋山港主航道附近岛屿众多，急涨水时，由于受汊道的影响，筲其岛和颗珠山附近的流向与主航道走向夹角可达20°，会导致重载船的操纵能力变差。港内航道边界紧邻码头泊位，锚地稀少，可仅供1艘大型船舶应急使用。目前，每天约有30艘大型船舶进行靠离泊作业，若大型船舶在发生紧急情况，几乎没有可用于大幅转向避让的可航水域。

2.3 网络训练与优化

网络训练学习的流程如下：1) 训练的初始，将随机值赋予各神经元之间的权值系数；2) 比较输出值与期望值的偏差，并改变各神经元间的权值；3) 误差或迭代次数达到预设值，则网络训练完成。

本文的训练算法采用traingd算法，该算法的特点是批梯度下降训练函数，从参数的负梯度方向调整权值、阈值；隐含层的传递函数为sigmoid函数，其定义式为

(10)

输出层采用线性传递函数。隐含层节点数的选择关系到网络训练的准确度和效率，节点数过多则神经网络过于复杂，计算量增大，延长收敛时间；节点数过少则无法保证训练的精确度。本文借鉴“黄金分割法”的概念[14]，隐含层的节点数范围由下面的经验公式来确定：

(11)

式中a、b分别为隐含层节点数的最小值、最大值；ni、no、ny分别为输入层、输出层、隐含层的节点数。

以下为采用黄金分割法搜索最佳隐含层节点数的步骤:

1) 本文中，ni=5，no=1，因此代入式(11)得出a=3，b=16。在区间[3,16]上确定第1个点的位置x1=a+0.618(b-a)=11.034，取x1=11并记录该点对应的误差。

2) 第2个点位置，x2=a+0.382(b-a)=7.966，取x2=8，记录该点对应的误差。

3) 比较x1、x2点对应的误差的大小，因x1点的误差较小，则留下区间[x2,16]。

4) 在区间[x2,16]上重复以上过程，比较点3、16、11、x1、x2等对应的误差，最终得到ny=16为区间[3,16]上最优值。

5) 用黄金分割法求得拓展区间[16,24]，右端值c根据16=3+0.618(c-3)取得。重复步骤1)～4)，最终求得区间[16,24]上的最佳值为ny=18。

6) 比较ny=16和ny=18时的误差，最终选取误差值较小的ny=16。

不同节点数的R、MRE和RMSE值见表3。

表3 不同节点数的评价指标

从表3可以看出，当隐含层节点数为16时，实测值与预测值的相关系数R较大且MRE与RMSE较小，因此本文中的隐含层节点数确定为16。为了减少训练的时长、减小误差，对样本的数据进行归一化处理；同时，数据在输出后需要反归一化处理。选取mapminmax函数作为归一化函数，归一化、反归一化表达式分别为

(12)

x=xmin+y(xmax-xmin)

(13)

式(12)、(13)中x为被归一化的值；xmin、xmax分别为x中的最小值、最大值；y为归一化后的值。

3 计算结果分析

建立BP神经网络模型，使用记录的175组试验数据中随机的150组进行模型训练，剩余的25组用于验证模型的精确程度。

图6显示了不同工况点(工况点指不同进口空气干球温度和湿球温度、喷淋水流量、截面风速、板片间距工况下测得的数据组，下文的“样本点”则是指所有工况点中被用作训练神经网络的一部分)下板片与空气间复合换热系数的预测值与实测值的对比。由图6可以看出，绝大多数预测值与实测值的偏差较小。评价标准有相关系数R、平均相对误差MRE、均方根误差RMSE，分别为0.999 2、0.355 94%、0.508 01 W/(m2·K)，最大的偏差为1.521 27 W/(m2·K)，最大偏差百分比为1.038 95%。

图6 复合换热系数K的预测值与实测值的对比

少数工况点处复合换热系数误差较大的原因可能是该点附近的训练数据较少，神经网络对这些样本点的训练并不充分；而那些预测准确性较高的点，其附近的训练数据足够多，神经网络对此处的训练足够充分。因此，若在后续的研究中对实验参数变化范围内的工况进行细化实验，获取更多的数据，将能进一步提高工况点预测的准确度。在横流式蒸发冷凝器中鼓泡式板片传热性能研究领域，BP神经网络可用于验证实验、数值模拟结果的准确性，并为进一步的鼓泡式板片设计优化和横流式蒸发冷凝器的改进提供参考。

图7显示了平均相对误差MRE随迭代次数增加的变化趋势。由图7可以看出，训练过程中随着迭代次数的增加，平均相对误差总体下降，并趋于稳定。

图7 平均相对误差随迭代次数的变化(学习速率0.1，训练函数traingd，隐含层神经元数16)

4 结语

根据鼓泡式板片在蒸发冷凝器蒸发侧的运行工况搭建了实验台，并基于BP神经网络建立了其在水-空气侧传热性能的预测模型。采用3层BP神经网络，以进口空气干球温度、进口空气湿球温度、喷淋水流量、截面风速及板片间距为输入层，以Sigmoid函数与线性传递函数分别作为隐含层和输出层的传递函数；隐含层神经元数为16，训练函数为traingd，输出参数为板片与空气间的复合换热系数，选取的迭代次数为40 000次。

影响鼓泡式板片换热性能的参数较多，使用BP神经网络在给定的输入输出参数基础上调整各神经节点的权值，从而对不同工况下的鼓泡板片复合换热系数进行预测，而不需要进行烦琐的全部实验流程。

以相关系数、平均相对误差、均方根误差作为网络评价指标，结果分别为0.999 2、0.355 94%、0.508 01 W/(m2·K)。在鼓泡式板片换热性能测试方面，本文建立的BP神经网络模型的预测结果与实验测得的换热系数相差很小，为不同工况下鼓泡式板片换热性能的预测提供了参考。