风电中空夹层钢管混凝土结构塔筒在往复扭矩作用下的破坏机理研究*

罗伟 陆国兵 兰涌森 谭继可 王宇航

1.中国船舶重工集团海装风电股份有限公司 重庆401122

2.重庆大学土木工程学院 400045

引言

风力发电钢塔筒是风力发电机组中主要的支撑结构，其作用是支撑机舱和叶轮，除了要承受叶轮传递的水平风荷载，还要承受叶轮和风机运行时产生的动荷载。因此，塔筒对于整机稳定运行起着重要作用。目前大型风电塔筒多采用钢制圆锥形筒壳结构，但这种结构在复杂荷载作用下容易发生失稳破坏，且近年来风力发电机组朝着单机大功率的趋势发展，导致风电塔筒高度更高，风电塔筒承担的荷载更大，传统钢制圆锥形筒壳结构难以满足承载需求。而中空夹层钢管混凝土塔筒具有截面刚度大、承载力性能好等优点，可满足大功率风电机组的荷载要求。

近年来，文献［1 ～3］对中空夹层钢管混凝土结构塔筒进行了整体可靠度分析和轴压试验，得到了不同分段数和上下截面直径比对承载力的影响，指出采用中空夹层钢管混凝土结构塔筒更适用于大功率风电机组。韩林海等［4-6］以钢管径厚比、空心率、长细比、偏心率为主要参数，进行了风电中空夹层钢管混凝土结构塔筒的轴心受压和偏心受压试验，提出了风电中空夹层钢管混凝土结构塔筒的轴压和偏压承载力实用计算方法。黄宏等［7-12］对风电中空夹层钢管混凝土结构塔筒的纯扭和压扭受力性能进行了试验和有限元研究，表明了风电中空夹层钢管混凝土结构塔筒具有较好的延性和较高的承载力，加载路径对其压扭受力性能影响不大，轴压比和长细比对其受扭承载力影响较大。郭立湘等［13，14］对方形截面风电中空夹层钢管混凝土结构塔筒的压扭受力性能进行了试验研究和有限元分析，并提出了方形截面风电中空夹层钢管混凝土结构塔筒的压扭承载力简化计算方法。Huang 等［15］研究了空心率和外钢管含钢率对风电中空夹层钢管混凝土结构塔筒构件轴压性能的影响，并提出了圆套圆和方套圆风电中空夹层钢管混凝土结构塔筒构件的受扭承载力计算公式。Wang 等［16］对风电中空夹层钢管混凝土结构塔筒构件在往复扭矩作用下的受力性能进行了试验研究，研究表明风电中空夹层钢管混凝土结构塔筒构件在受扭荷载作用下具有较好的耗能性能和变形能力。

基于风电塔筒底部受力大、上部受力较小的特点，为了充分发挥钢塔筒和中空夹层钢管混凝土塔筒各自的优点，同时为了节省材料和减轻整个塔筒结构自重，本文提出了一种上部钢塔筒和下部中空夹层钢管混凝土结构塔筒的混合结构塔筒。中空夹层钢管混凝土塔筒作为整个风电塔筒的关键受力构件，目前国内外学者主要研究了不同截面类型的风电中空夹层钢管混凝土结构塔筒构件的静力行为，对往复荷载下风电中空夹层钢管混凝土结构塔筒的耗能和破坏机理研究较少。本文采用有限元数值模拟的方法，进步一研究风电中空夹层钢管混凝土结构塔筒在往复纯扭荷载作用下的变形过程和破坏机理，并与已有试验结果进行对比。基于风电中空夹层钢管混凝土结构塔筒截面特性，提出了受扭承载力简化计算公式，为风电中空夹层钢管混凝土结构塔筒的抗扭性能研究和工程应用提供参考。

1 新型装配式混合结构塔筒

风电塔筒具有底部受力较大，而上部受力较小的特点，本文结合风电塔架结构的这一受力特点，基于钢-混凝土组合结构的基本受力原理，提出了一种新型混合塔筒—基于预制边缘加劲组合壳体的装配式混合塔筒。如图1 所示，其上部为纯钢塔筒，下部为中空夹层钢管混凝土塔筒，其中下部中空夹层钢管混凝土塔筒由预制边缘加劲组合壳体拼装而成，并沿竖向分段组装，所有节点均采用螺栓连接。预制边缘加劲组合壳体由外层钢板、中部混凝土、内层钢板以及周边的钢结构边缘加劲区构成。本文对下部中空夹层钢管混凝土塔筒展开研究。

2 有限元分析

2.1 有限元建模

基于ABAQUS通用有限元软件进行数值模拟计算，根据试件尺寸和分析精度采用合适的单元，选用合适的混凝土本构和钢材本构，定义相关参数模拟钢材和混凝土接触面的相互作用关系，选用合理的网格尺寸等，以空心率和不同截面形式为研究参数，建立风电中空夹层钢管混凝土结构塔筒有限元模型，通过比较数值模拟计算结果与试验结果，验证有限元模型的精确性。其中，圆形截面风电中空夹层钢管混凝土结构塔筒有限元模型CC-T1、CC-T2 空心率分别为0.52 和0.71，矩形截面（或方形截面）RRT1、RR-T2（SST1、SS-T2）空心率分别为0.48（0.35）和0.60（0.69）。

图1 风电中空夹层钢管混凝土结构塔筒Fig.1 Schematic diagram of steel-concrete-steel double-skin composite shell tower

1.模型单元类型

结合钢管和混凝土的截面尺寸和长度尺寸的大小关系，本文ABAQUS有限元模型中，采用实体单元模拟夹层混凝土的受力行为，采用壳单元模拟内钢管和外钢管的受力行为。

2.钢材和混凝土本构

材料的本构关系是材料宏观受力性能的综合体现，选取合理的材料本构关系对有限元数值模拟的准确性有很大影响。本文中采用二次流塑本构模型描述钢材的应力-应变关系，钢材的应力-应变关系可按式（1）计算。采用混凝土塑性损伤模型模拟夹层混凝土的损伤开裂行为，混凝土的应力-应变关系采用韩林海［17］提出的适用于ABAQUS 计算的混凝土应力-应变关系，见式（2）。混凝土塑性损伤参数采用余志武［18］等提出混凝土损伤变量计算方法进行计算。

式中：Es＝206000N／mm2，εk＝10εy，Et＝0.01Es。

其中，x ＝ε／ε0，ε0＝εc+800ξ0.2×10-6，εc＝（1300 +12.5f′c）×10-6，y ＝σ／σ0，

3.界面接触属性

风电中空夹层钢管混凝土结构塔筒柱在受扭过程中，钢管与混凝土之间将出现相对位移，钢管将约束混凝土的变形，本文采用在ABABQUS中定义接触属性模拟钢管与混凝土之间的界面相互作用行为，采用“penalty”函数定义钢管与混凝土界面切向摩擦受力行为，摩擦系数为0.6［17］。在混凝土与钢管的接触界面上，混凝土的法向变形受到钢管的约束，故采用硬接触定义钢管与混凝土界面法向相互作用关系。定义界面相互作用关系时，将混凝土定义为主面，将钢管定义为从面。

4.边界条件

根据风电中空夹层钢管混凝土结构塔筒在试验过程中的边界约束情况确定其有限元模型的边界约束。本文采用固端约束定义风电中空夹层钢管混凝土结构塔筒有限元模型中钢管和混凝土底部六个自由度上的位移，既保证了有限元模型底部钢管和混凝土形成一个截面整体又保证了边界条件为固接。在模型顶部定义参考点，将模型顶部的钢管单元和混凝土单元与参考点耦合在一起，从而使有限元模型顶部钢管和混凝土形成截面整体，并通过参考点对有限元模型顶部钢管和混凝土同步施加位移荷载，如图2 所示。文献［16］中试件往复受扭是通过对刚性顶梁施加往复位移荷载实现的，且试验装置的几何关系已知，可通过试验装置的几何关系将试验加载端位移变化量换算成试件顶部扭转角变化量［19］，本文将试验加载点的位移加载制度换算成参考点的扭转位移加载制度，进而保证有限元模型边界与试验边界条件相同，从而实现有限元分析时施加扭矩与试验时施加扭矩相同。

5.网格划分方法

确定模型网格尺寸时，应兼顾模型的计算精度和计算效率，本文在划分网格时，在截面上采用按边布置种子划分网格，在模型高度方向采用全局布置种子划分网格，采用结构化划分网格的方法对模型进行网格划分，模型网格划分如图2所示。

图2 网格划分和边界条件Fig.2 Mesh and boundary condition

2.2 结果对比

1.扭矩-扭转角滞回曲线对比

有限元数值计算得到的扭矩-扭转角滞回曲线和文献［16］中试验得到的扭矩-扭转角滞回曲线吻合较好，如图3 所示。在整个试验加载过程中，当扭转角较大时，圆套圆风电中空夹层钢管混凝土结构塔筒的受扭承载力未出现下降；矩形套矩形风电中空夹层钢管混凝土结构塔筒和方套方风电中空夹层钢管混凝土结构塔筒在扭转角较大时，受扭承载力达到峰值，继续加载，受扭承载力开始出现下降，空心率较大的矩形套矩形和方套方风电中空夹层钢管混凝土结构塔筒的受扭承载力下降较快，由于有限元模型采用的材料本构模型与实际材料的真实本构关系存在一定的差异，有限元分析得到的滞回曲线较试验曲线饱满。

图3 试验曲线与有限元结果对比Fig.3 Comparison of calculated and tested T-θ hysteresis curves

2.外钢管破坏形态对比和分析

风电中空夹层钢管混凝土结构塔筒的整体破坏形态和外钢管Mises 应力分布如图4 所示，在往复扭矩作用下，外钢管均出现显著的剪切变形和向截面外侧的鼓曲变形。由于混凝土对钢管起到一定的约束作用，圆套圆风电中空夹层钢管混凝土结构塔筒在往复扭矩作用下，外钢管出现整体膨胀的变形趋势，进而进一步增大了圆套圆风电中空夹层钢管混凝土结构塔筒的截面抗扭惯性矩，从而导致了受扭承载力持续增大。从图4a

中可见，在扭矩作用下圆套圆风电中空夹层钢管混凝土结构塔筒的外钢管底部应力和应变较大，相同应变下，由于油漆的受拉强度较小，外钢管底部油漆层首先撕裂并脱落，有限元数值模拟也表明外钢管底部的应力较大，有限元模拟结果与试验吻合较好。矩形套矩形和方套方风电中空夹层钢管混凝土结构塔筒在往复扭矩作用下，外钢管出现了与水平向呈45°的褶皱带状鼓曲，褶皱带状鼓曲随着往复扭矩呈现交替变形，持续加载，两条褶皱带状鼓曲的顶端和拐点重合的区域处于反复弯折的变形状态，并最终呈现低周疲劳开裂，如图4b、c所示。

3.内钢管破坏形态对比和分析

有限元数值模拟得到的内钢管在往复扭矩作用下的鼓曲变形和Mises 应力分布如图5 所示，可见有限元数值模拟结果与试验结果吻合较好。从图5a中可见内钢管上有明显的环向划痕，这表明在实际加载过程中，钢管与混凝土之间有相对滑动，进一步证明有限元模型中采用摩擦系数考虑钢管与混凝土之间的相互作用关系是合适的。在往复扭矩作用下内层钢管变形与外钢管类似，均是在往复扭矩作用下交替出现斜向鼓曲的褶皱变形，且随着扭矩的增大，鼓曲褶皱变形逐渐增大。由于混凝土的约束作用，内钢管向截面空心内侧鼓曲变形。有限元模拟结果与试验结果均可见圆套圆风电中空夹层钢管混凝土结构塔筒内钢管在往复扭矩作用下的破坏变形不显著，而矩形套矩形和方形套方形风电中空夹层钢管混凝土结构塔筒内钢管在往复扭矩作用下均出现显著的鼓曲变形，结合风电中空夹层钢管混凝土结构塔筒在往复扭曲作用下外钢管的破坏变形特征，结果表明圆形套圆形风电中空夹层钢管混凝土结构塔筒的受扭承载力和受扭变形性能均优于方形套方形和矩形套矩形风电中空夹层钢管混凝土结构塔筒。

4.混凝土截面应力分析

扭矩作用下，混凝土截面上的剪应力分布如图6 所示。因试件截面对称，从图中可见截面上剪应力沿截面呈反对称分布。从图6b、c 中可见矩形截面和方形截面风电中空夹层钢管混凝土结构塔筒中混凝土截面剪应力最大值出现在截面长边中部区域。

图4 破坏模式对比（单位： MPa）Fig.4 Comparison of failure mode between test specimens and FEA mode（unit：MPa）

图5 内钢管破坏对比（单位： MPa）Fig.5 Failure of inner steel tubes（unit：MPa）

图6 混凝土应力分布（单位： MPa）Fig.6 Stress distribution of sandwich concrete（unit：MPa）

3 破坏机理分析

在扭矩荷载作用下，风电中空夹层钢管混凝土结构塔筒截面将出现剪应力，如图7 所示，通过应力分析可知主拉应力和主压应力分别与风电中空夹层钢管混凝土结构塔筒轴线方向呈45°。对混凝土而言，当最大主拉应力大于混凝土的抗拉强度时，混凝土开裂。由于圆钢管平面外刚度较大以及混凝土约束了钢管平面外变形，圆套圆风电中空夹层钢管混凝土结构塔筒中的外钢管出现膨胀鼓曲变形，进而分担截面更多的扭矩荷载；内钢管出现向截面内方向的微小鼓曲变形，由于内钢管两端部出现应力集中，内钢管两端附近的钢管鼓曲变形比中部鼓曲变形略大。

矩形套矩形和方形套方形风电中空夹层钢管混凝土结构塔筒中钢管的平面外刚度较小且混凝土对钢管仅有单面约束作用，当扭矩作用下钢管上产生的应力超过钢管屈服强度时，受约束最弱的钢管中部区域将出现和主拉应力方向相同的斜向褶皱鼓曲；在正向扭矩和反向扭矩交替作用下，外钢管斜向褶皱鼓曲方向交替变化，如图8所示，交替出现的褶皱鼓曲顶点和拐点交汇点处钢材变形幅度最大，随着加载-卸载往复次数的增加，由于钢材损伤不断积累，钢材开裂，且裂缝沿垂直于主拉应力方向扩展；内钢管中部区域平面外刚度较小，内钢管两端受到的约束强于内钢管中部区域，在正向扭矩和反向扭矩交替作用下内钢管中部区域将向截面内侧鼓曲变形，进而内钢管的截面受扭模量进一步减小，内钢管分担的受扭承载力逐渐减小。

图7 风电中空夹层钢管混凝土结构塔筒受扭Fig.7 Steel-concrete-steel double-skin composite shell under torsion

从图4 和图5 中可见，空心率对往复扭矩荷载作用下风电中空夹层钢管混凝土结构塔筒的破坏模式影响较小，空心率主要决定了内钢管的材料分布和内钢管径厚比（或宽厚比），进而影响风电中空夹层钢管混凝土结构塔筒的承载力和延性。

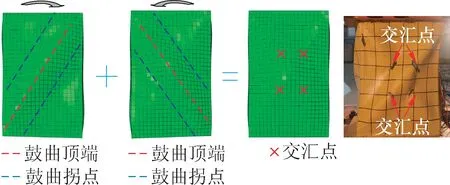
图8 外钢管破坏机理分析Fig.8 Failure mode analysis of outer steel tubes

4 简化计算公式

4.1 公式推导

扭矩荷载作用下风电中空夹层钢管混凝土结构塔筒中的混凝土与外钢管的相互作用改变了外钢管的破坏变形形态，使得外钢管在径厚比（或宽厚比）较大时，钢材材料强度仍能够充分发挥作用，即外钢管在出现鼓曲变形时，钢管截面应力均已经达到其材料屈服强度；混凝土与内钢管之间相互作用很小，但内钢管的径厚比（或宽厚比）较小，仍可通过控制内钢管的径厚比（或宽厚比）使得内钢管再出现鼓曲变形时，内钢管截面应力均达到其材料屈服强度。本文假定风电中空夹层钢管混凝土结构塔筒受扭破坏时，内钢管和外钢管截面应力均达到其屈服强度，忽略钢管与混凝土之间相互作用对混凝土强度的影响，从风电中空夹层钢管混凝土结构塔筒中内钢管、混凝土和外钢管等材料的截面分布特征可见其截面抗扭承载力主要由夹层混凝土（Tc）、外钢管（Tso）和内钢管（Tsi）三部分承担，本文提出风电中空夹层钢管混凝土结构塔筒的抗扭承载力计算公式为：

夹层混凝土的抗扭承载力计算可按素混凝土抗扭公式计算，且钢管对夹层混凝土具有一定的约束作用，不考虑混凝土抗拉强度的降低，故夹层混凝土抗扭承载力计算公式为：

式中：ft为混凝土抗拉强度，；Wt为混凝土截面受扭模量。

箱型截面受扭模量：

式中：bh和hh分别为箱型截面的宽度和高度；hw为箱型截面的腹板净高；tw为箱型截面壁厚。圆环形截面受扭模量：

式中：do和di分别为混凝土圆环外径和内径，如图9 所示。

图9 截面示意Fig.9 Section diagram

外钢管和内钢管为薄壁闭口钢管，由于夹层混凝土的约束作用，扭矩荷载作用下的钢管能够充分发展塑性，外钢管和内钢管的截面抗扭承载力计算公式如下：

式中：τoyv＝0.58fyo、τiyv＝0.58fyi分别为外钢管和内钢管抗剪强度，fyo和fyi分别为外钢管屈服强度和内钢管屈服强度；to、ti分别为外钢管和内钢管壁厚；A0为钢管壁厚中线围成的面积。

4.2 结果验证

将本文提出的计算公式与文献［15］中的试验结果进行计算对比，结果见表1，其中Tue为试验结果，可见计算精度较好，计算结果偏于安全。

单调加载下钢材的应力-应变关系曲线与循环加载下钢材的应力-应变关系不同，循环荷载作用下的钢材将出现强度强化现象，循环强化作用可使钢材的屈服强度提高近20%［20］。对比本文提出的受扭承载力简化公式计算结果与文献［16］屈服强度试验结果，如表2 所示，可见简化公式计算结果与试验结果吻合良好。

综上可见本文提出的风电中空夹层钢管混凝土结构塔筒受扭承载力简化计算公式有较好的计算精度，可用于工程设计参考。

表1 简化计算模型计算结果与文献［15］试验结果对比Tab.1 Comparison between test result［15］and simplified model result

表2 简化计算模型计算结果与文献［16］试验结果对比Tab.2 Comparison between test results［16］and simplified model results

5 结论

本文通过建立风电中空夹层钢管混凝土结构塔筒有限元模型，研究了往复受扭下的风电中空夹层钢管混凝土结构塔筒的受力行为，得到如下结论：

1.本文建立的“壳-实体”风电中空夹层钢管混凝土结构塔筒有限元模型能较好地模拟风电中空夹层钢管混凝土结构塔筒在往复扭矩荷载作用下的受力和变形行为，有限元计算结果与试验结果吻合较好，空心率对扭矩作用下风电中空夹层钢管混凝土结构塔筒的破坏模式影响很小。

2.圆套圆风电中空夹层钢管混凝土结构塔筒具有较好的受扭承载性能，能承受较大的扭矩变形，在整个加载过程中受扭承载力未出现显著下降，圆套圆风电中空夹层钢管混凝土结构塔筒在往复扭矩作用下的破坏模式为端部受扭撕裂破坏，有限元模拟结果也表明圆套圆风电中空夹层钢管混凝土结构塔筒受扭时底部应力较大。在实际工程中，应加强塔筒底部的设计和连接。

3.矩形套矩形和方套方风电中空夹层钢管混凝土结构塔筒具有较好的受扭承载性能，但在往复扭矩作用下的破坏形态为外钢管截面边长较大的一侧出现褶皱带状鼓曲，且褶皱带状鼓曲随着扭矩加载方向变化而交替变化，钢管与混凝土分离，降低了风电中空夹层钢管混凝土结构塔筒的受力性能。

4.风电中空夹层钢管混凝土结构塔筒在往复扭矩作用下的破坏特征均是钢管受力发生局部鼓曲破坏，从而钢管与混凝土分离，可通过在钢管上布置栓钉或者其他形式的抗拔键，进一步增强钢管与混凝土之间的连接，从而增强风电中空夹层钢管混凝土结构塔筒的组合工作性能，更好地发挥钢材的受力性能。

5.本文基于组合结构基本原理，提出了用于计算风电中空夹层钢管混凝土结构塔筒受扭承载力的简化计算公式，有较好的计算精度，可用于工程参考。