基于随机调制超表面的差分关联成像方法研究

年毅恒 周宁宁 朱士涛 张安学

(西安交通大学信息与通信工程学院多功能材料与结构教育部重点实验室 西安 710049)

1 引言

近年来，雷达成像技术得到不断发展，其有效拓展了雷达的功能，使得雷达不仅仅局限于测距和探测，还可以用于获取目标和场景的图像[1]。雷达成像技术在军用及民用领域有着广泛的应用。目前，高分辨雷达成像系统主要采用合成孔径雷达(Synthetic Aperture Radar,SAR)与逆合成孔径雷达(Inverse Synthetic Aperture Radar,ISAR)方式，二者均利用距离-多普勒原理，其距离向分辨率取决于发射信号的带宽，方位向分辨率取决于目标与雷达相对运动产生的多普勒频移[2,3]。然而在几何观测条件不理想和目标非合作等情况下，SAR/ISAR成像效果将会受到极大制约。

雷达关联成像(Radar Coincidence Imaging,RCI)作为一种新的凝视高分辨率成像技术，借鉴光学成像中的鬼成像方法[4]通过阵列构造以及对发射信号进行波前随机调制，构造在时间和空间上随机分布的二维随机辐射场，以此模拟具有随机涨落的光场分布[5]，其方位向分辨不再依赖目标与雷达之间的相对运动，而是利用了辐射场不同方向信号分布的差异性。但其探测效率低，难以广泛应用。

基于随机调制超表面的关联成像方法利用超材料表面对微波信号进行随机调制来构造随机辐射场[6]，其利用超材料对电磁波灵活频率调控特性，通过超表面上多个单元对不同频率下的辐射信号进行随机空间调制[7–9]，在此基础上每一个超表面单元可以等效为一个辐射单元，每一个频点下的电磁波信号可作为一次随机探测模式。该方法降低了系统设计的复杂性且避免了雷达阵列间的相互干扰。但其存在探测模式、辐射单元独立性不足等问题，导致随机辐射场的时空相关性较大[10]，从而影响成像质量。

针对此问题，本文提出一种基于超表面的差分关联成像(Differential Coincidence Imaging,DCI)模式，当参考场的某一个辐射样本随机性不强时，可通过不同辐射样本之间的差分构造新的样本，降低不同探测模式之间的相关性，使得不同网格位置处的相关函数达到比较理想的情况，提升了成像质量。同时，提出了一种特殊的差分关联成像，通过特殊的波前调制利用参考场样本差分来获取参考场的梯度信息，称为梯度关联成像(Gradient Coincidence Imaging,GCI)。其可以在不获取图像的情况下，在算法处理过程中获取目标方位向的边缘信息，提高对目标的检测分辨性能。通过数值仿真验证了本方案的正确性。

本文各章节内容介绍如下：第1节对本文的主要研究背景及研究内容进行了介绍；第2节建立了基于随机调制超表面的关联成像信号模型，分析了成像误差，并与差分关联成像方法相结合，给出了具有鲁棒性的基于超表面的关联成像方法；第3节介绍了梯度关联成像方法，对其成像分辨率进行了分析；第4节通过仿真实验验证了本文理论分析的正确性。

2 成像模型与差分关联成像方法

2.1 成像模型

对于传统的光学鬼成像，计算鬼成像方法是通过预置好的散斑加载到空间光调制器上来产生随机光场。基于此，一种基于超表面的微波关联成像方法(Spatial Modulation Coincidence Imaging,SMCI)被提出[6]，其利用超表面对入射信号进行随机调制来产生二维随机辐射信号。

电磁超材料是由亚波长结构单元通过周期或非周期排布组成的人工复合结构，由于其奇特的电磁特性，可实现一系列电磁波调控功能，例如异常反射、异常折射、电磁隐身、极化转换等。电磁超表面是超材料的二维形式，具有低剖面、低损耗、低成本及便于设计制造等优势。其可以利用平面内超材料突变的相位或者幅度来调控电磁波的空间上的相位或者幅度分布，从而达到控制电磁波传播的目的。电路相位型是超表面在微波频段常见的设计方式，其具有典型的“三明治构型”的基本单元结构：最底层是金属背板，中间夹层是介质基板，顶层是图形化的金属图案层。电磁波照射会使金属图案层产生等效电容L和电感C，通过改变图案层的形状可以影响二者的大小，从而实现基本单元所“引入”的突变相位的调控[11]。对于透射式超表面，可将其等效为导纳Z的电磁阻抗表面，当电磁波从自由空间中垂直照射，穿过超表面并透射到自由空间中，忽略时谐因子，则超表面的透射相位和反射相位分布可以表示为

当突变相位满足一定随机特性时，可以将其视为对入射信号的随机调制。雷达发射端发射信号至超表面，通过随机调制，超表面上的每一个单元将作为随机辐射单元产生独立电磁波信号，辐射至成像区域；雷达每发射1个频率的信号产生1次与其他探测模式不相关的探测模式，从而产生二维随机辐射场。通过接收信号与参考场的关联对目标区域进行成像[6]。

发射信号为St(fm,t)，其中fm代表一次探测模式的中心频率，则在超表面上的信号可以表示为

其中，z代表超表面区域，rsn代表其上的各个反射单元，一共有N个反射单元，τ代表从发射端到超表面的时延，通过超表面各单元进行调制后的信号可以表示为

其可以代表每一个超表面单元的辐射信号，其中φ(rsn,fm)代表每一个单元在每一个频点下的随机相位调制。每个超表面单元的透射幅度可以近似认为相等，这一假设可以通过超表面单元设计实现。则辐射至成像区域的信号可以表示为

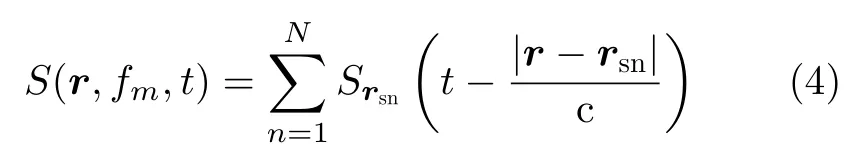
其中，r代表成像区域的网格点位置，式(4)代表了参考信号。成像区域的散射点反射信号至接收端，接收信号可以表示为

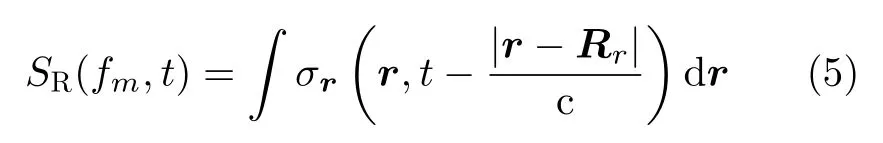
其中，Rr代表信号接收端位置，接下来对接收回波以及计算得到的参考场进行相干检波去除时间项，然后补偿参考场与接收端的时延。参考信号以及接收信号则可以分别写为S(r,fm)以及SR(fm)。然后在基本相关法的基础上求参考场与接收端的相关函数即可求出成像区域各网格点处的散射系数为

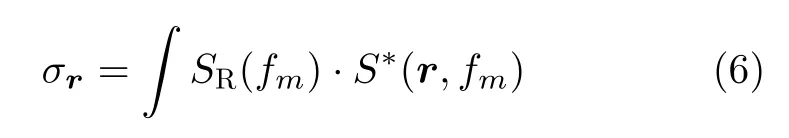
以上为基于随机调制超表面关联成像的成像与信号模型。由于SMCI中的参考场信号是超表面的每一个单元辐射至成像区域产生的。为方便后文对差分以及梯度关联成像方法的分析，可将其等效为无互耦合的理想阵列，采用多发单收模式。

在SMCI中的发射信号St(fm,t)，可以表示为

其中，A(fm)代表在不同频点下的信号幅度，,Tp为脉冲宽度。则可将式(2)每一个辐射单元的辐射信号等效为在雷达发射阵列中，每一个阵元的发射信号为

其中，rsn代表第n个阵元的位置，即对应式(2)中的每一个超表面辐射单元。

当成像区域满足远场条件时，在同一距离单元下不同方位向的网格点可以看作对于发射阵列的不同斜视角θ，下面对参考辐射场信号进行推导。如图1所示，设有N个发射阵元排成均匀线阵，阵元间隔为d，中心距离为r0，则对于该距离单元视角为θ的网格点的探测信号如式(9)所示。以阵列最左边的阵元为基准，其他阵元与它相比其波程差为

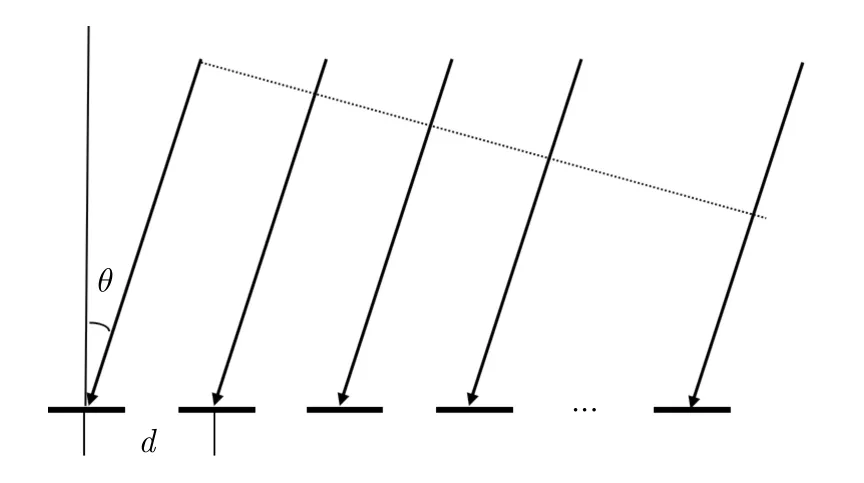
图1 线性阵列信号模型示意图Fig.1 Linear array signal model

2.2 差分关联成像方法与原理

关联成像是利用参考场的非相关性来分辨不同方位向的散射点，参考场不同网格处一阶关联统计特性代表了分辨能力。根据上文的等效信号模型分析，以基本相关法为基础，参考场中不同的方位向网格点的关联函数可以表示为

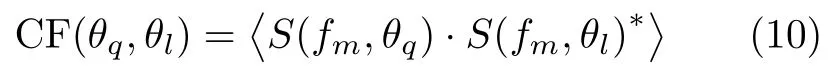
其中，θq和θl代表不同的方位向，fm代表第m个频点下的探测模式，〈·〉表示求所有探测模式下的数值平均。在SMCI中，不同频点下的发射信号幅度可以设为一致，且其不随超表面单元调制而改变，因此可将A(fm)视为1来进行计算。根据式(9)和式(10)进行进一步求解可得

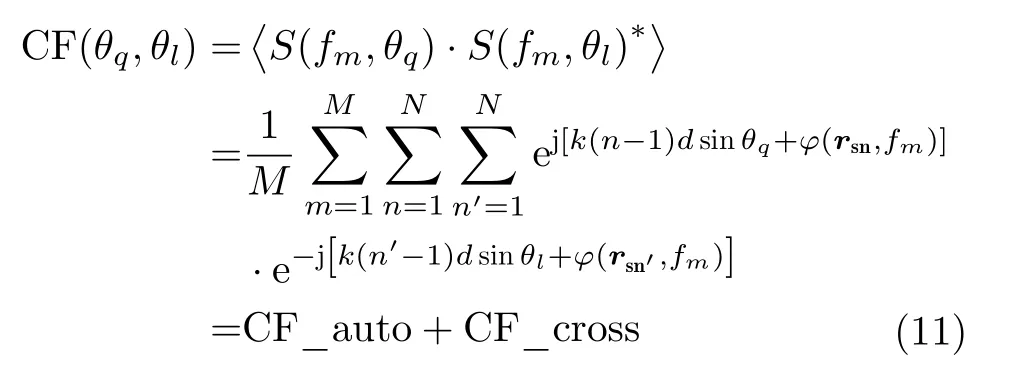
在式(12)中，当固定θq，改变θl时，可近似看作线阵波束指向为θq的方向图，代表了系统对不同方位向的分辨能力。式(13)为互相关项，为干扰项，该项的存在将会影响成像质量，甚至出现无法成像的情况。当超表面的随机相位调制均为任意相位的均匀分布即独立探测模式数较多时，式(14)的相位可看作在[0,2π]范围内的均匀分布，在该理想情况下，互相关项近似为0，可以去除该干扰项的影响。而由于实际情况中超表面的各辐射单元并不是相互独立的，即独立探测模式不足，对相位的调制无法满足任意相位的随机均匀分布，则该互相关项将会对成像质量产生较大影响，且成像效率不足。为解决这一问题，本文提出了一种基于随机调相超表面的差分关联成像模式，下面介绍其方法及原理。

在差分关联成像中，可利用两次不同探测模式样本的差分作为一组探测模式。将每次探测模式进行相干检波，根据式(9)，经过差分后的探测模式下的参考场信号可以表示为

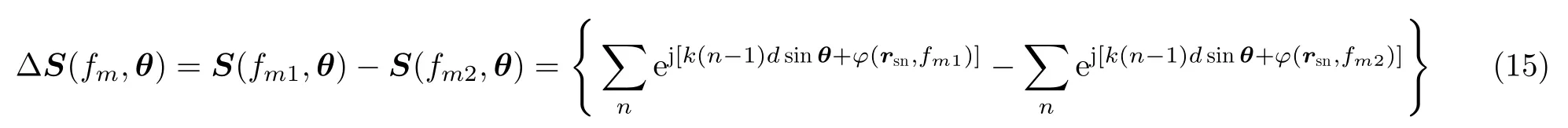
其中，m代表经过差分后的第m组探测模式，m1和m2代表直接经过超表面调制后的两次样本，θ代表各网格点所在位置的角度。则相关函数可以表示为

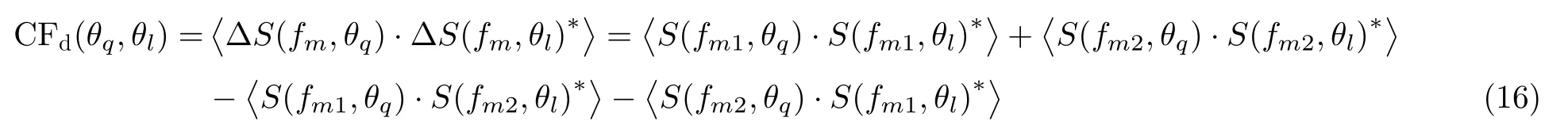
对比式(13)，差分关联函数的互相关项可以表示为

在上文的分析中，当独立的探测模式不足时，式(14)中的独立随机相位数量较少。而在式(17)中，差分关联函数增加了互相关项中的独立随机相位，在进行叠加后，使得互相关项降低，更加接近于0。差分关联成像即在保持独立探测模式不变的情况下增加了独立随机相位，从而降低了互相关项的干扰。因此式(16)可以表示为

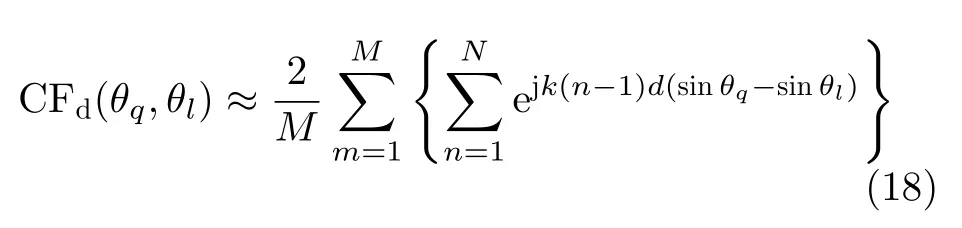
3 梯度关联成像方法与分辨率分析

在光学关联成像中，可以通过对散斑的移动来获取目标的边缘信息，称为梯度鬼成像[13–15]。类比于此，根据对超表面的特殊设计，可以使得一组探测模式的两个参考场满足在空间中的平移性，利用二者之间的差分来获取参考场的梯度信息。其可以在不获取图像的情况下，直接在成像过程中提取出目标方位向的边缘信息。梯度关联成像可以看作差分关联成像的一种特殊情况，差分关联成像是对任意探测模式相减求相关函数来降低互相关项，相减的两个样本可以看作一组探测模式。而在梯度关联成像中，一组探测模式中的两个样本应满足严格的关系，即参考辐射场的方位向平移。因此在对超表面单元设计时，不仅要满足不同组探测模式下调制相位的随机性，同时要使得一组内两次调制相位满足固定的关系。通过波前调制的方式使得一组探测模式的参考场应满足如式(19)所示的关系

其中，fm1和fm2代表第m组探测模式下的两个样本，∆θ代表成像区域方位向相邻网格点的方位角度差。现分别利用各组探测模式的两个样本对雷达区域进行照射，接收到的回波信号为

其中，σ代表散射系数向量，Sr1和Sr2代表两组探测模式下经相干检波后的接收信号。这里为方便表示，没有写出从参考场到接收阵元的距离校准，在具体处理中，对接收信号进行一个相位校准即可。获取不同方位向目标的边缘信息可以表示为

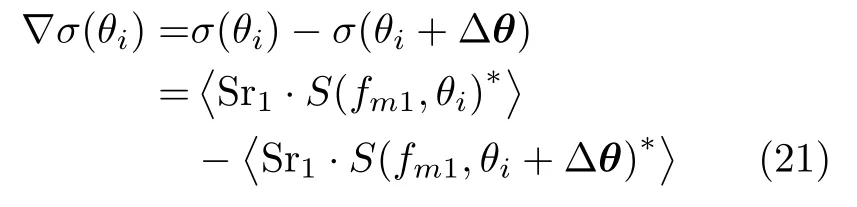
对式(20)中的两项进行相减，并根据式(19)和(21)可得

因此，对任一方位向θi，其边缘信息可以表示为

根据上面的分析，在梯度关联成像中，可以在不用获取目标图像的情况下，直接提取目标的边缘信息。需要在对发射信号进行波前调制时满足式(19)。

实现梯度关联成像根本上要实现一组探测模式下随机辐射方向图在方位向上的平移，因此可以利用“编码超表面”可控、可编程的人工超表面理念来实现对一组探测模式下两种随机辐射场的严格控制。在设计与应用中，将相位区间进行离散化处理，并对相应的超表面单元进行二进制编码，因而超表面结构的每种单元排布方式对应一个编码序列[16]。现仍以一维均匀线阵为例说明两次样本对信号的调制方式。在第m组探测模式的第1个样本下，可以采用对每一个阵元添加的随机相位不变，同时对各阵元加入各相应项的移相器α(∆θ)

根据式(9)可知，对超表面的任一组探测模式的两次相位调制满足上式的条件下，可以使得任一组探测模式下的两个参考场样本满足梯度关联成像所需要的情况。

式(23)代表了提取目标边缘信息的方式，则可以通过参考场的梯度信息与参考场求相关函数来表征梯度关联成像中目标边缘的模糊函数信息，如式(25)所示

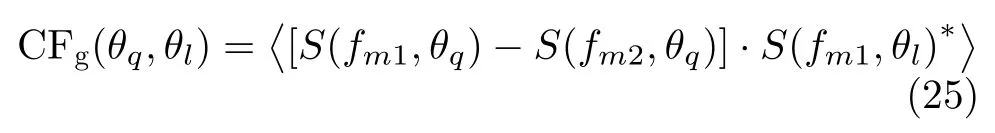
当固定θq,θl取任意角度，式(25)即代表了对方位向θq处边缘提取的分辨能力。根据式(9)及式(25)进行进一步推导，且考虑在理想情况下，互相关项为0，可得

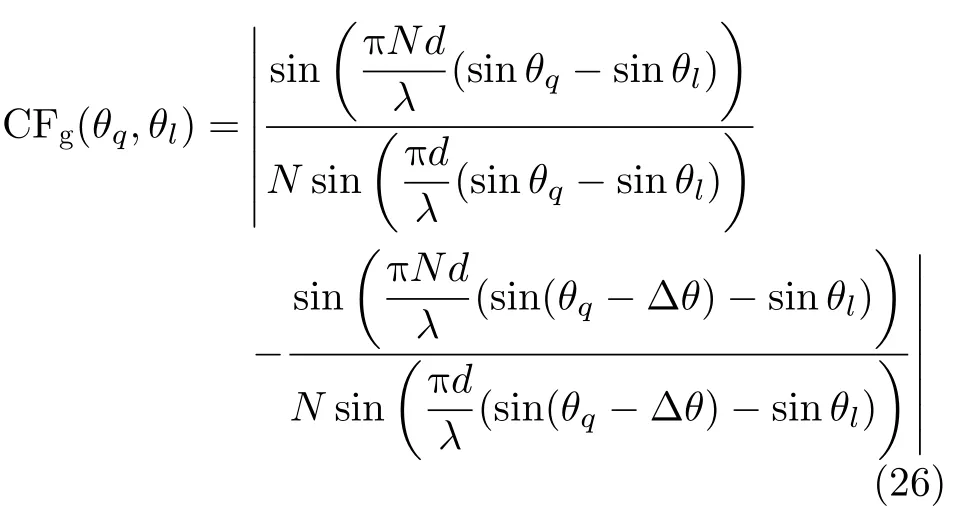
式(26)即为单个点目标在方位向上的边缘，在第4节中，将通过数值仿真对其进行分析。

4 仿真与结果分析

本节通过数值仿真对上文中的分析进行验证。在远场条件下，对相同距离单元不同方位向的分辨可以看作对不同角度的分辨。通过对比不同的波前调制情况来验证差分关联成像的可行性，并利用第3节中的方法进行数值仿真来验证梯度关联成像的可行性及其对分辨性能的提升。

在本次仿真中，载频为1 GHz，超表面单元数目为20个，单元边长为0.15 m，参考场样本数为100个，即在传统关联成像中，利用100个探测模式；在差分和梯度关联成像中，均利用50组探测模式，每组探测模式共有2个前者的探测模式样本。

首先考虑在同一距离单元，角度范围为–90°～90°。对于100个探测模式，20个超表面单元均进行随机相位调制，且随机相位不满足理想情况下的分布[17]，考虑到随机相位调制超表面的相互独立探测模式不足，即各超表面单元加入的随机相位不满足理想情况，可利用超表面中调制相位的非独立性来模拟超表面的相位调制。比如令随机相位满足(−π,π)的非均匀分布，较多相位存在线性关系，且相位较多集中分布在(−0.5π,0.5π)，其他参数不变。现以30°为基准作为观察视角，与其他角度求相关函数，得到的结果为方位角30°处的点扩展函数。由于每次仿真的相位均为随机加入，因此进行100组蒙特卡罗仿真，最终得到结果如图2(a)所示，红色为传统关联成像，蓝色为差分关联成像，可以看出传统的关联成像副瓣较高，对结果会产生较多干扰，即互相关项较高，而差分关联成像则降低了这一项的干扰，验证了第2节的理论分析。同时以0°为基准作为观察视角，与其他角度求相关函数，得到的结果为方位角0°处的点扩展函数，则结果如图2(b)所示，得到了同样的情况，通过不同的观察角度进一步验证了差分关联成像的有效性。

同时对比第2种情况下的不同探测模式的相关系数，传统关联成像共有100个探测模式，以第50个样本为基准与所有样本求解相关系数。在差分关联成像中共有50个探测模式，以第50个样本与所有样本求解相关系数，结果如图3所示，可以看出差分关联成像在不改变探测模式数量的情况下明显降低了相关系数。

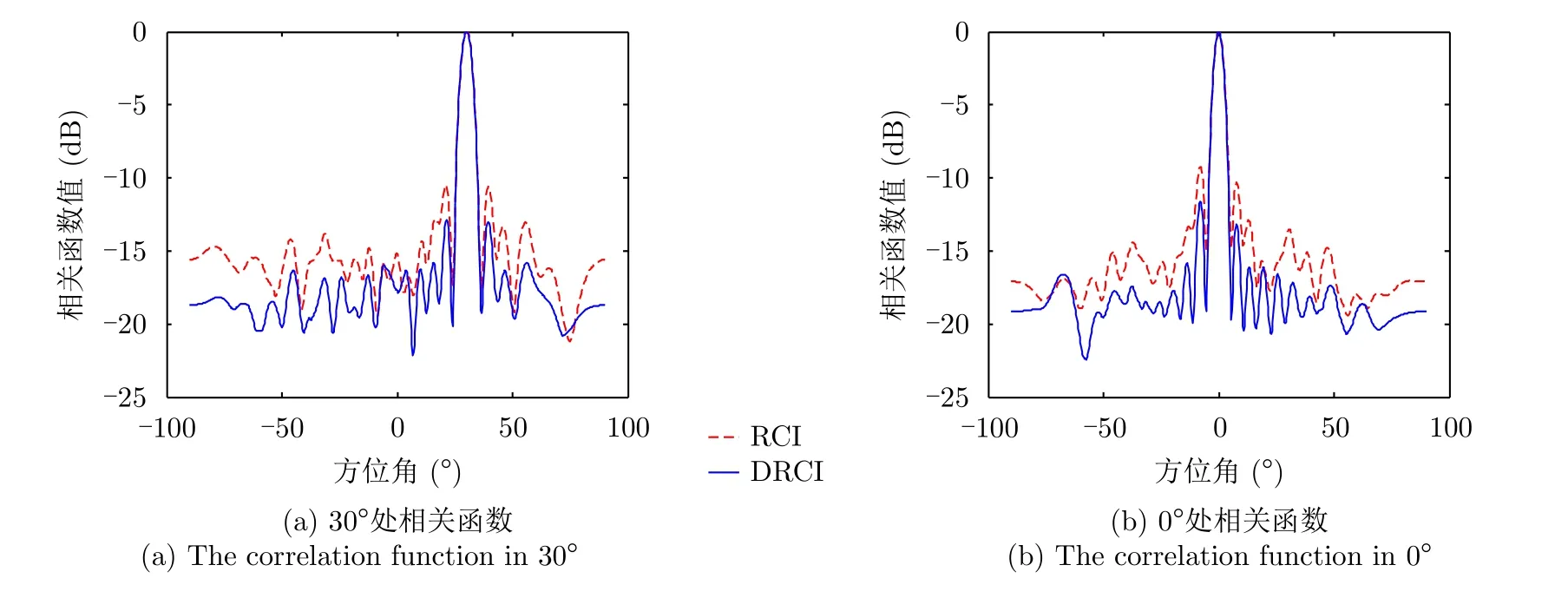
图2 差分关联成像相关函数Fig.2 The correlation function in differential coincidence imaging

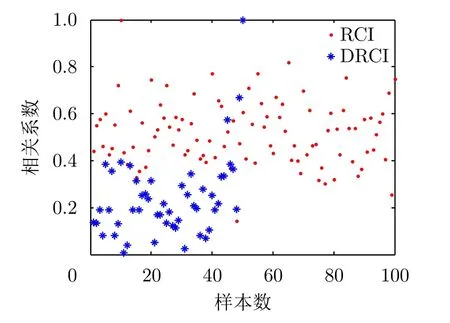
图3 传统与差分关联成像不同辐射样本的相关系数Fig.3 The correlation coefficient of detection modes in coincidence imaging and Differential Coincidence Imaging (DCI)

现仍以30°为基准作为观察角度，求参考场梯度与参考场的相关函数，对比其结果与传统关联成像的结果如图4(a)所示，可以看出，利用梯度关联成像可直接获取该散射点的边缘信息，且根据主瓣的3 dB宽度，可看出梯度关联成像的两个主瓣更窄，分辨性能更强，而带来的损失则是第1副瓣电平升高。同时，保持超表面边长不变，考虑在不同单元数目下的两种成像方式的主瓣宽度，即角度分辨率，如图4(b)所示，可以看出，随着阵元数目的增大，两者的分辨率都得到降低，而梯度关联成像的分辨率始终低于传统关联成像，说明梯度关联成像带来了对目标分辨的提升。而对若干次仿真进行统计平均，可得传统关联成像的第1副瓣电平约为–13 dB，而梯度关联成像的第1副瓣电平约为–9 dB。对于后者而言，在提升了分辨性能的同时，也带来了副瓣的升高。

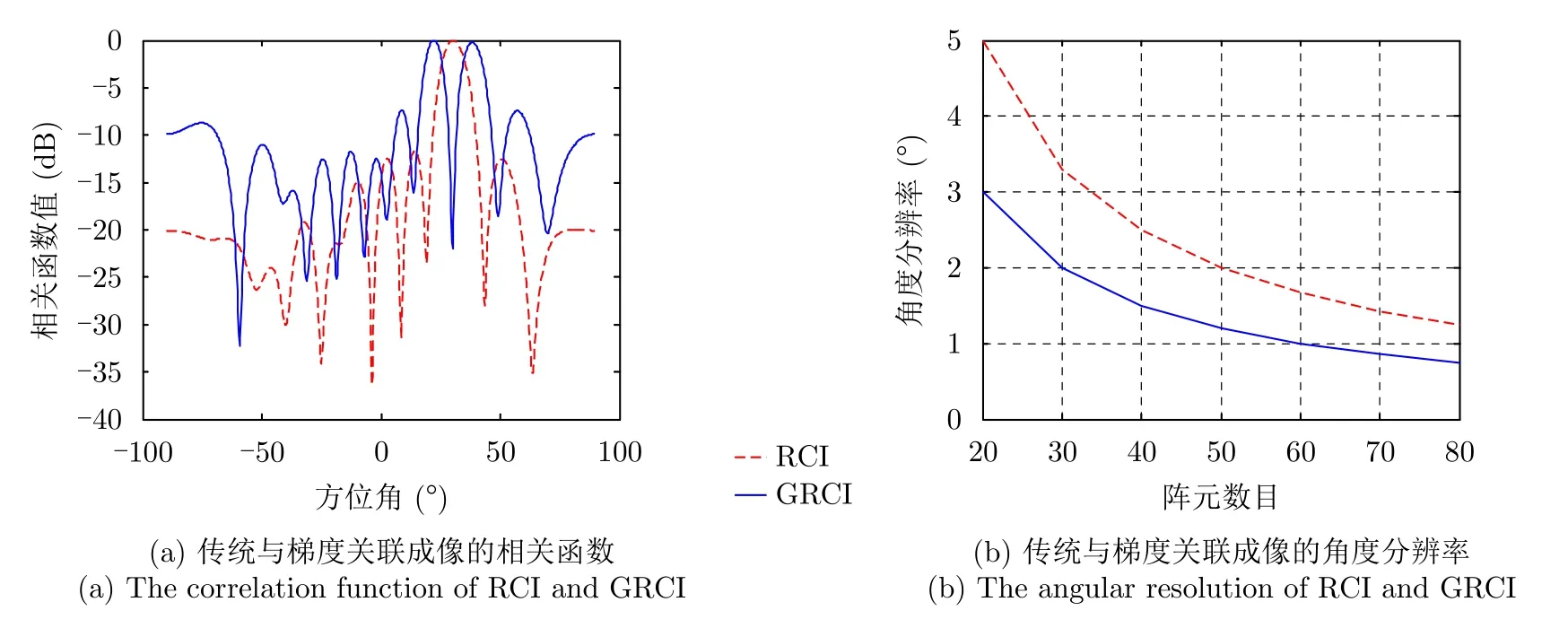
图4 传统与梯度关联成像的对比Fig.4 The comparion between coincidence imaging and Gradient Coincidence Imaging (GCI)

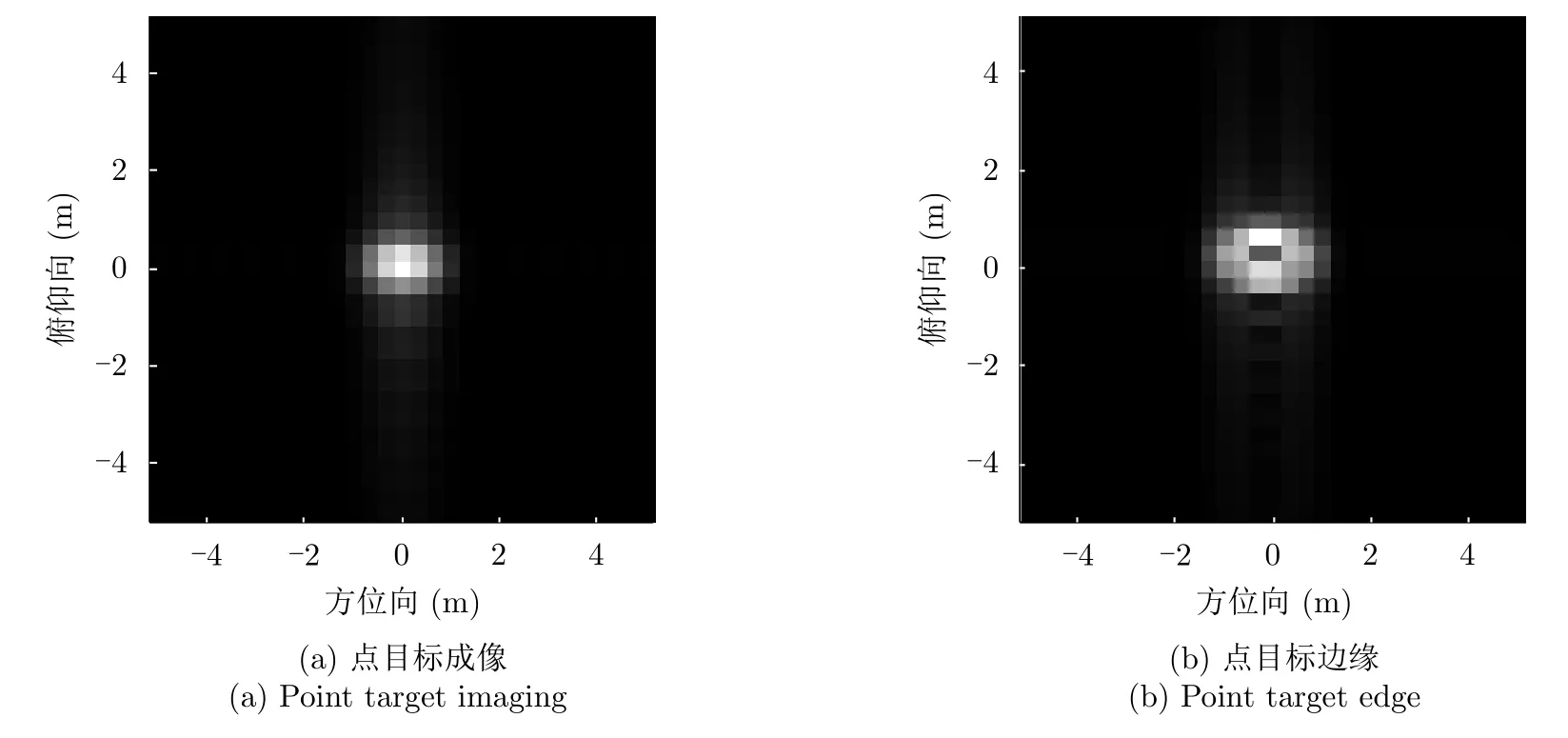
图5 传统关联成像与梯度关联成像对比Fig.5 The comparion of imaging between coincidence imaging and Gradient Coincidence Imaging (GCI)

进行单个点目标的仿真实验，超表面单元为二维分布，则可对目标进行方位-俯仰的二维成像。如图5所示，二者分别为在传统关联成像下获得的点目标二维图像，以及在梯度关联成像下获得的点目标边缘。根据二者的对比可以看出梯度关联成像可以在不获取目标图像的情况下直接获取目标的边缘信息，且对边缘的分辨能力超过了对目标的分辨能力。

5 结论

针对超表面探测模式不足的问题，本文以参考辐射场空间分布一阶统计特征为基础，建立了基于随机调制超表面的关联成像信号模型，将其等效为基于雷达阵列的关联成像模型，对差分关联成像方法进行了分析，推导了在该方法下的参考场相关函数，证明了其可以有效降低探测模式间的相关系数，提升成像质量。同时，对一种特殊的差分关联成像方法—梯度关联成像方法进行了介绍，对成像分辨率进行了分析，证明了其可以有效提升关联成像系统对目标边缘的提取能力。最后，通过仿真实验验证了本文理论分析的正确性。