超宽带宽角极化不敏感的电路模拟吸波材料设计

姚智馨 肖绍球*②

①(电子科技大学物理学院 成都 611731)

②(中山大学电子与信息工程学院 广州 510275)

1 引言

吸波材料可以定义为一个空间电磁(Electro-Magnetic,EM)滤波器，在特定的工作频段内既不反射也不透射入射到其表面的电磁能量。Salisbury[1]吸波材料于20世纪50年代被提出，由阻性材料层和导电平板组成，两者之间的距离为1/4波长。该吸波材料结构简单，但吸波带宽很窄。Knott等人[2]使用多层阻性层来增加带宽，但同时会导致剖面高度上升。近十年来，以有耗频率选择表面(Frequency Selective Surface,FSS)为损耗层的电路模拟吸波材料被提出并得到了迅速的发展，逐渐被证明是高性能吸波材料设计的最有效方法之一。

传统的吸波材料设计往往只针对电磁波正入射情况。文献[3]提出了一种基于有耗方环FSS的宽带吸波材料，实现了112%的带宽，整体剖面高度为0.104λL。Shang等人[4]引入了有耗双方环FSS阵列来获得3个谐振点，当厚度为0.088λL时，获得了126.8%的带宽。在文献[5]中，作者设计了一种新型石墨烯可调谐宽带吸波材料，通过调节石墨烯材料的化学势，在太赫兹频段实现了56.5%的吸波带宽。文献[6]利用焊接集总电阻的周期性金属条阵列实现了91.9%的百分比带宽，当入射角度上升至45°时，吸收率降至60%。Zhang等人[7]在聚甲基丙烯酸甲酯上制备了一种由透明的氧化铟锡聚对苯二甲酸乙二酯薄膜组成的齿轮形单元，在超宽带范围内实现了118.1%的吸波带宽。国外相关论文利用合适方法在工作频段内实现了超宽带的吸波性能[8–12]。国内学者针对超宽带低剖面吸波材料设计提出了卓有成效的研究成果。于家傲等人[13]利用双六边形的电路模拟吸波材料得到了129.6%的吸波带宽以及0.084λL的厚度，实测与仿真结果吻合情况良好。文献[14]提出一种基于集总电阻加载的小型化超宽带超材料吸波体结构，该结构通过纵向级联的方式，结合上下两层吸波体结构实现了151%的吸波带宽，整个吸波体的单元大小仅为0.089λL×0.089λL，厚度为0.078λL。文献[15]采用3层氧化铟锡FSS结构实现了149.0%的百分比带宽以及0.090λL的剖面高度。

在正入射超宽带吸波材料设计的同时，由于FSS阵列、空间波阻抗等对电磁波入射角的敏感性，吸波材料的吸波性能会随入射角的增大而恶化明显。当入射角度大于30°时，将不能保证90%以上的电磁波吸收。由于实际应用中电磁波并不总是垂直入射，因此提高斜入射，尤其是大角度情况下吸波材料的吸波性能具有重要意义。

目前很少有研究在超宽带低剖面吸波材料设计的同时考虑双极化角度稳定性。文献[16]提出了一个由3层不同尺寸的方形电阻超表面组成的宽带宽角吸波材料，吸波带宽与角度分别达到137%、45°，但在横电(Transverse Electric,TE)极化电磁波45°斜入射时，吸收率恶化至80%。文献[17]提出了一种由有耗平面交叉阵列和垂直环形阵列组成的宽带宽角吸波材料，吸收角增加到50°，剖面为0.09λL，但正斜入射时的公共带宽仅为48.6%。宽角阻抗匹配层自21世纪初逐渐被应用于宽带宽角扫描相控阵的设计中[18]。由于吸波材料和天线可以看作一对互易器件，本文尝试根据互易原理来改善斜入射吸波性能。本文在传统的方环吸波材料的基础上添加了由两层无耗FSS构成的宽角阻抗匹配层。与传统的吸波材料相比，TE和TM(Transverse Magnetic)两种极化情况下的最大吸波角均由30°增加到45°，正入射时的吸波带宽达到137.1%，且在111.1%的公共带宽内实现了至少10 dB的正斜入射反射系数衰减。

2 吸波材料结构设计

所设计宽带宽角吸波材料的结构如图1所示。整体结构由上而下依次为由两层无耗方环FSS构成的宽角阻抗匹配层、一层有耗方环FSS以及导电金属平板，各层之间填充空气介质。在阵列单元模型中，为了加快整体计算、优化速度，宽角阻抗匹配(Wide Angle Impedance Matching,WAIM)覆盖层中两层无耗方环FSS的结构尺寸被设定为完全相同，电介质基板的厚度与相对介电常数依次为h0和εr1。损耗层则由导电金属方环和一层介质基板组成，每条金属边上嵌入集总电阻以引入热损耗，介质衬底的厚度与相对介电常数分别为h3,εr2。本设计采用相对介电常数为3.55的Rogers 4003作为WAIM和损耗层的介质衬底，即εr1=εr2=3.55。

2.1 等效电路模型

等效电路方法是电路模拟吸波材料设计与分析中最为有效的方法之一。由以往文献可知，方环FSS的等效电路为串联电感电容支路，介质则可以等效为一条长度相同的传输线模型。因此，整个吸波材料的等效电路模型由一个串联RLC电路、两个串联LC和6条传输线组成，如图2所示。电路元件L1和C1表征WAIM层中的方环FSS，而R2,L2和C2对应有耗层FSS。结构从上到下的WAIM层基板、空气间隔层1、空气间隔层2、有耗层基板和空气间隔层3分别等效为长度h0,h1,h2,h3,h4的传输线。Y0和Y1为空气和介质基板的特性导纳，同时随入射角以及电磁波极化的变化而改变。电磁波入射的自由空间也被等效成特性导纳为Y0的入射端口。两种极化条件下特性导纳的计算表达式如式(1)和式(2)所示。

图1 吸波材料结构示意图Fig.1 The unit cell geometry of the absorber

图2 所设计具备宽角阻抗匹配层的吸波材料等效电路模型Fig.2 The equivalent circuit for absorber with WAIM layer

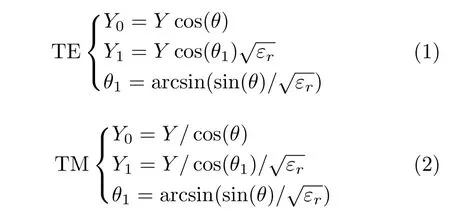
2.2 反射系数计算

由等效电路模型可知反射系数的计算表达式为

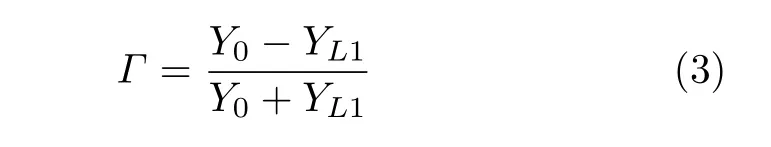
其中，

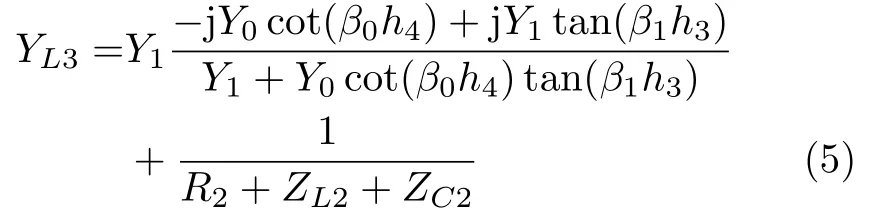
β0和β1分别为空气和介质基板中电磁波的传播波数

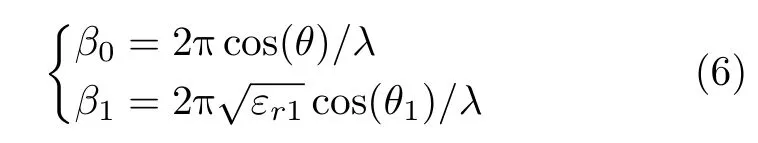
为了得到斜入射时等效电感和电容的计算表达式，本文从最基本的周期性无线长线阵出发。由文献[19]可知，等效电路为并联电感的周期性无线长阵列在TM极化下的反射系数表达式为

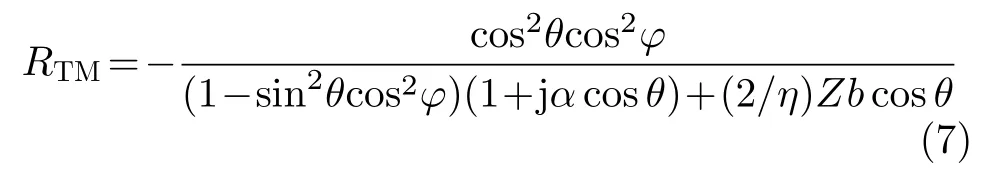
其中，Z为线阵表面的单位长度损耗，在理想金属条件下为0；α称为网格参数，在文献[19]中给出，θ和ϕ分别为球坐标系下的俯仰角和方位角。对于TM极化，式(7)可以进一步简化为

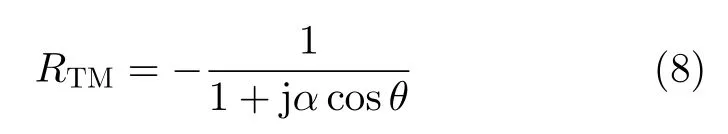
本文由二端口矩阵的ABCD方法得到反射系数的计算公式为

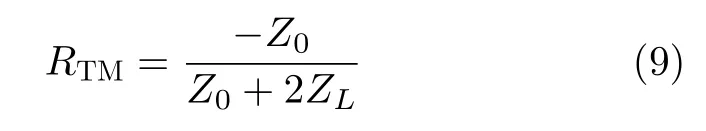
其中，ZL和Z0分别为FSS表面阻抗和空间特性阻抗。将式(8)、式(9)相结合可以得到式(10)结论

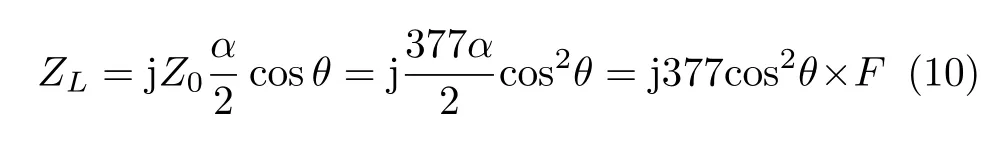
F为文献[20]给出的计算函数。利用相同的计算方法可以得到电感等效时TE极化下表面阻抗的计算公式

进一步，结合Babinet原理，可以得到电容等效时TE,TM极化下表面导纳的计算公式为

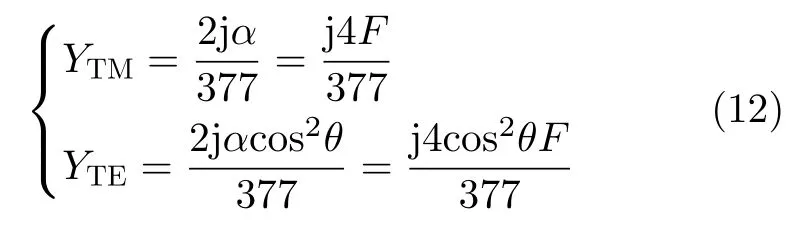
综合可得TE极化和TM极化斜入射条件下方环FSS等效电感与电容的最终表达式为

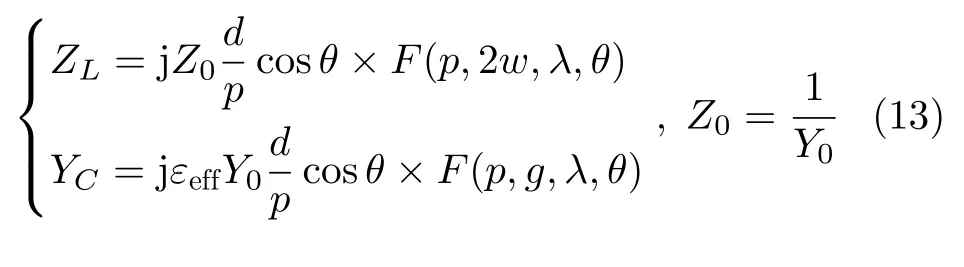
Y0的值如式(1)和式(2)所示。εeff是介质基板引入的有效相对介电常数[21]，p,w,d,g是方环FSS的尺寸参数。

2.3 差分算法的参数优化

利用2.2节提出的计算公式，一旦确定吸波材料的结构参数，可快速、准确地计算得到正斜入射情况下的吸波性能。进一步结合差分进化算法，就能得到特定优化目标下的最优尺寸结果。对于所设计的吸波材料，假设频率范围为1～8 GHz，优化目标为TE,TM双极化正、斜(45°)情况下公共吸波带宽的最大值，可以优化得到最终的频率响应结果如图3所示，对应的结构尺寸参数为p=15 mm,w=1.5 mm,g=0.2 mm,w1=4 mm,g1=5 mm,h0=1.7 mm,h1=4.5 mm,h2=0.9 mm,h3=1.3 mm,h4=17.9 mm,R2=200 Ω。由图3可知，在垂直入射下，反射系数至少降低10 dB的百分比带宽可达140.0%，而在入射角增加到45°时，TE和TM极化下的吸波带宽分别为147.8%和126.5%。公共频带为1.8～6.4 GHz，对应百分比带宽为112.2%。

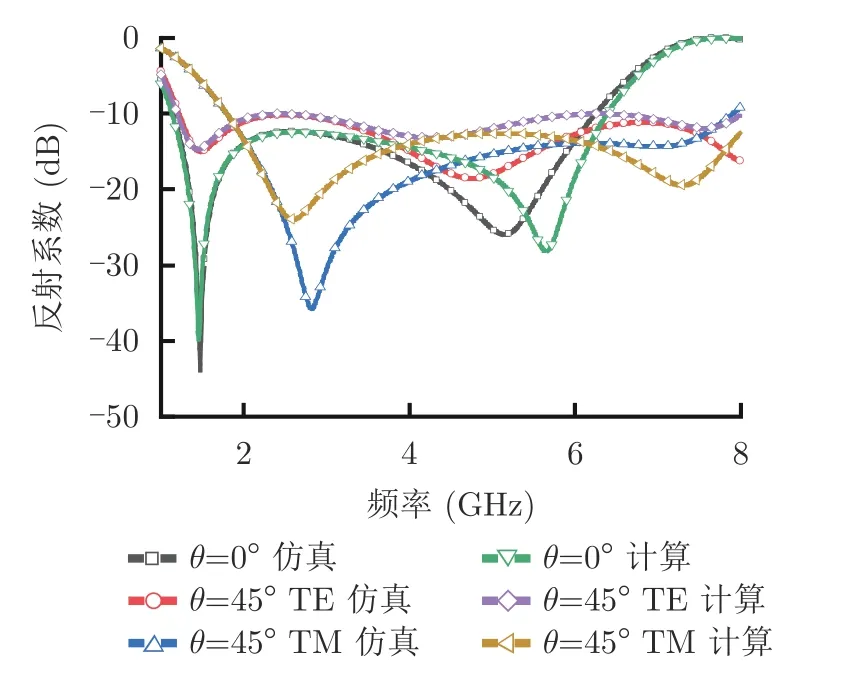
图3 算法计算与软件仿真分别得到的正斜入射情况下最优反射系数结果Fig.3 The optimal reflection coefficient under normal and oblique incidence obtained by calculation and simulation

为深入了解宽角阻抗匹配层的实际作用机理，本文将图2所示的等效电路模型简化，如图4所示。Ylayer1,Ylayer2,YRLC2和YGND分别代表两层无耗WAIM层、损耗层和金属平板对输入导纳的作用。众所周知，输入导纳虚部零点是反射系数谐振频点产生的必要条件，即

以TM极化电磁波入射为例，若只考虑YRLC2和YGND，可以很容易地计算得到正斜入射情况下两者虚部的频率响应结果，如图5所示。由传播常数的表达式(6)可知，随着入射角的增大，空气和介质基板的电长度逐渐降低，BGND总体曲线下移。由于BRLC2在低频段保持稳定，因此在没有WAIM层作用的情况下，低频段正入射情况下实现的阻抗匹配在斜入射下将逐渐失配，导致斜入射性能恶化明显。另外，在高频段，RLC支路的电纳值随入射角度的上升而上升，从而部分抵消基板电纳的下降，保证斜入射时较高的导纳匹配效果及吸波性能。同理，针对TE极化波可以得到完全相似的结论。也就是说，提高斜入射时吸波材料吸波性能的关键即在TM极化的低频段和TE极化的高频段分别引入随入射角上升而增大的电纳值。

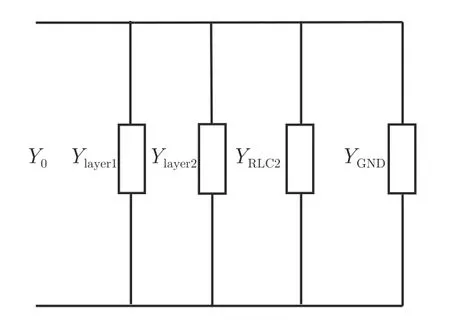
图4 为了分析简化得到的等效电路模型Fig.4 The simplified equivalent circuit model for analysis

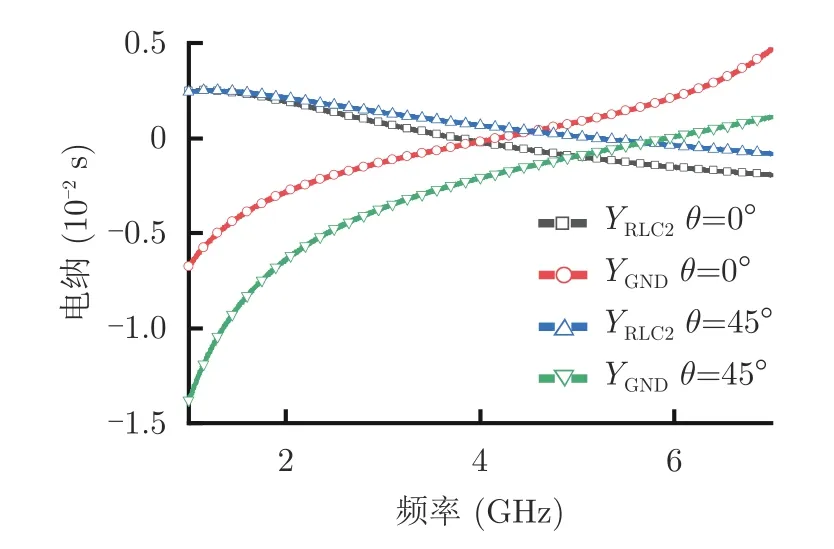
图5 YGND和YRLC2在TM正斜入射时的电纳值Fig.5 The susceptances of YGNDand YRLC2under normal and oblique incidence for TM-polarized wave

图6给出了TM极化条件下WAIM层中Ylayer1和Ylayer2在正入射和斜入射下虚部的频响结果。结果表明，随着入射角的上升，这两个电纳值均在低频段增大，从而部分抵消了之前提到的BGND下降。也就是说，只要能够保证正入射时的导纳匹配，在斜入射时同样能够实现良好的匹配效果，进而大大改善了吸波材料在TM极化下角度稳定性。图7给出了有无宽角阻抗匹配层分别得到的斜入射反射系数结果，可以看出，在WAIM层的作用下，斜入射时的吸波带宽明显增加。对于TE极化可以利用相同的分析方法得到相似的结论。

进行差分算法参数优化之后，需要以得到的结构参数为初始值在CST等仿真软件中建立全波仿真模型，并进一步利用参数扫描等手段优化得到最终的尺寸参数结果，即为p=15 mm,w=1.6 mm,g=0.4 mm,w1=1 mm,g1=9 mm,h0=1.5 mm,h1=6 mm,h2=2.4 mm,h3=1.5 mm,h4=1mm,r=133 Ω。相应的反射系数结果同样在图3给出。结果表明，利用软件仿真得到的正斜入射反射系数结果和公式计算值具有较高的相似性，从而验证了等效电路以及数学模型的准确性。另外，正入射、TE斜入射和TM斜入射时的百分比吸波带宽分别为138.3%,147.1%和126.5%，3个吸波频段的公共交叉部分为1.8～6.3 GHz，对应百分比带宽为111.1%。

3 实验测试

为验证所设计模型的准确性，本文加工、制作了13×13个单元的样件进行实验测试，如图8所示，总尺寸为195 mm×195 mm。各层之间填充PMI泡沫材料防止FSS由于自身重量导致的中心内陷，并采用对吸波性能影响极小的尼龙柱串联起来。具体的测试装置如图9所示，将两个喇叭天线放置在同一侧，分别用来发射和接收电磁波信号。另一侧在距离喇叭天线约1.5 m(位于喇叭天线的远场区)的距离分别放置测试样品、相同尺寸的金属平板以及无样品。具体的测试流程及数据处理方法如文献[4]所示。

图6 Ylayer1and Ylayer2在TM极化正斜入射时的电纳值Fig.6 The susceptances of Ylayer1and Ylayer2under normal and oblique incidence for TM-polarized wave

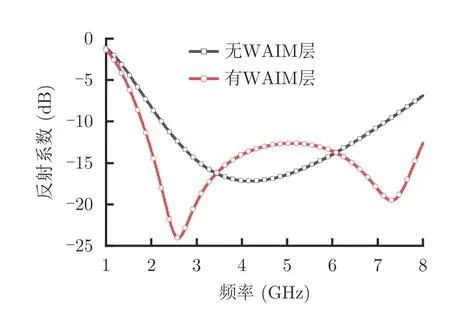
图7 有无宽角阻抗匹配层对应的TM极化斜入射反射系数结果Fig.7 Reflection coefficient under TM-polarized oblique incidence with and without WAIM layer

图8 加工样品Fig.8 Fabricated sample

图9 反射系数测试装置示意图Fig.9 Measurement setup for reflection coefficient

在电磁波正、斜入射下测得的反射系数如图10所示，并同样给出仿真结果进行对比。结果表明，所设计的吸波材料在正入射时能够实现137.1%的吸波带宽，正斜入射时的公共吸波频段为1.7～5.9 GHz，对应的百分比带宽为110.5%。虽然加工误差引起了一定的频率偏移，但计算结果与仿真、实测结果仍有较高的相似性。本文进一步给出了所设计吸波材料和以往文献成果在吸波带宽和吸波角度方面的比较，如表1所示。由于以往的文献大多集中在正入射时，表中给定的吸波带宽对应正入射时的吸波性能。结果表明，由于WAIM层的存在，所设计的吸波材料以较小的剖面高度增大为代价，实现了最大的吸波带宽以及较大的吸波角度。

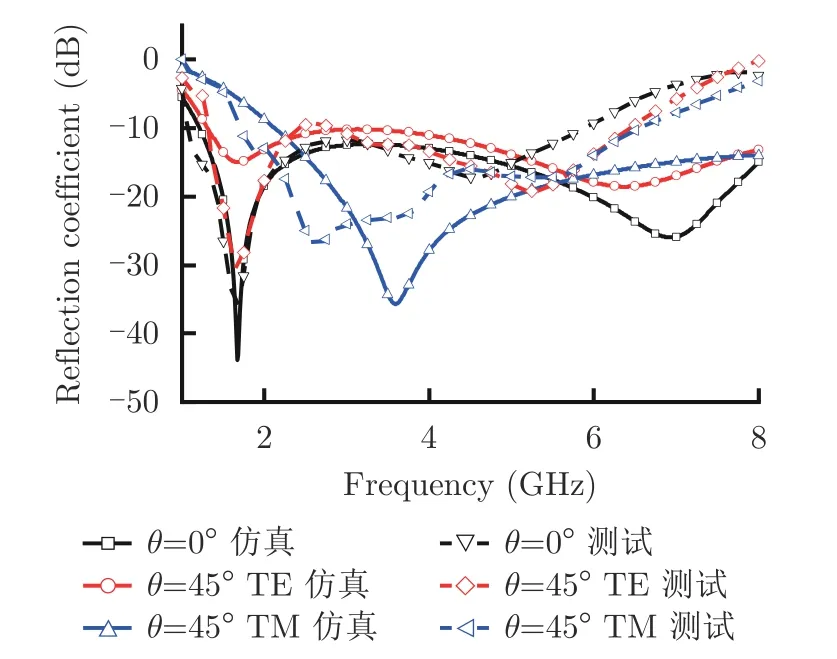
图10 实验测试得到的正斜入射情况下反射系数结果Fig.10 The optimal reflection coefficient under normal and oblique incidence obtained by simulation

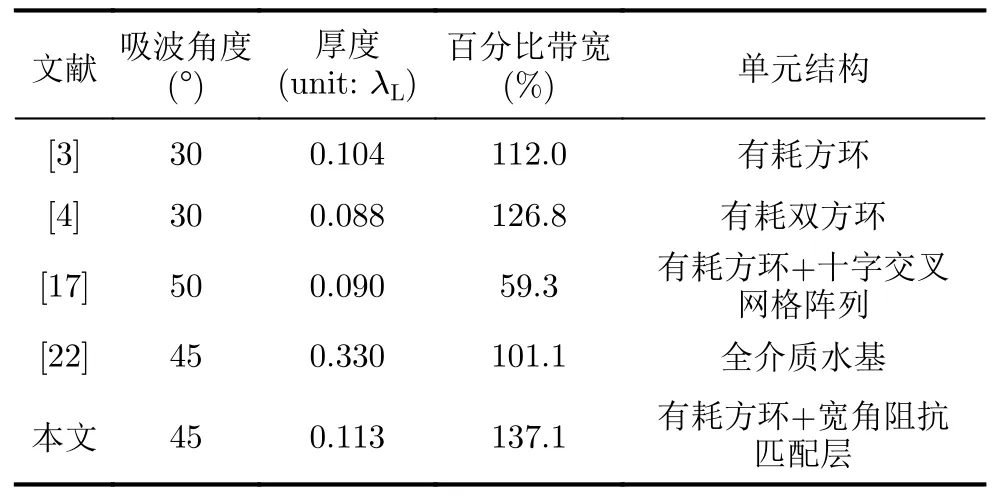
表1 吸波性能对比Tab.1 Comparison of performance

4 结论

本文在传统方环吸波材料的基础上，通过采用合适设计的宽角阻抗匹配层结构，在保证大角度吸波的同时实现了数倍频的超宽带吸波性能。利用等效电路和输入导纳分析，深入研究了入射角对吸波性能的影响以及WAIM层在改善斜入射方面的作用。通过等效电路计算、仿真和测试，将正入射和斜入射条件下反射系数实现至少10 dB衰减的公共带宽提高到111.1%(3.5:1)。与已有的设计相比，所设计的吸波材料具有较大的吸波角度和工作带宽，有助于改善军用系统的隐身特性和运行安全性。