对藏棋“久”的分阶段算法研究

沈强望　丁濛　杜文涛　赵文龙

摘要：藏族久棋是2019年中国计算机博弈锦标赛新设棋种，在此之前，国内外对该棋种的博弈策略研究相对较少。本文基于久棋两个博弈阶段规则和目的差异性大的特点，提出一种分阶段的博弈策略：下子阶段，考虑到无明显胜负判别的因素，提出一种基于相对胜负的改进蒙特卡洛树搜索算法以获取最佳下子点;行棋阶段，考虑到过程中的行棋方式会对后续模拟局面造成一定的影响，提出一种加入过程分值的改进Alpha-Beta剪枝搜索算法以获取最优行棋方案。在上述算法模拟博弈树的过程中，通过下子阶段优先集中在中心区域，行棋阶段优先形成褡裢的估值策略，给出了一份完整的估值评估表。实验结果表明，使用上述博弈策略及估值表实现的博弈程序棋力较高。

关键词：Alpha-Beta剪枝;蒙特卡洛树搜索;计算机博弈;藏棋

【Abstract】TibetanJiuqiisanewchesstypeinthe2019ChinaComputerGameChampionship.Priortothis，therewererelativelyfewresearchesonthegamestrategyofthischesstypeathomeandabroad.BasedonthelargedifferencesinrulesandobjectivesbetweenthetwogamestagesofJiuqi，thispaperproposesastagedgamestrategy：currentstage，takingintoaccountthefactorsthathavenoobviouswinorlosejudgment，animprovedMonteCarlotreesearchalgorithmisproposedbasedonrelativewinsandlossestoobtainthebestmovepoint;inthechess-movingstage，consideringthatthechess-movingmethodintheprocesswillhaveacertainimpactonthesubsequentsimulationposition，animprovedAlpha-Betapruningsearchalgorithmwithprocessscoresisproposedtogetthebestchessplan.Intheprocessofsimulatingthegametreewiththeabovealgorithm，currentstageisprioritizedtofocusonthecentralarea，andthechess-playingstageprioritizestheformationofacomprehensivevaluationstrategy，andacompletevaluationevaluationtableisgiven.Theexperimentalresultsshowthatthegameprogramachievedbyusingtheabove-mentionedgamestrategyandvaluationtablehashigherchesspower.

【Keywords】Alpha-Betapruning;MonteCarlotreesearch;computergame;Tibetanchess

作者簡介：沈强望（2000-），男，本科生，主要研究方向：计算机博弈;丁濛（1982-），男，博士，副教授，主要研究方向：可视媒体处理、计算机博弈;杜文涛（2000-），男，本科生，主要研究方向：计算机博弈;赵文龙（2000-），男，本科生，主要研究方向：计算机博弈。

0引言

随着人工智能的不断发展，人们对计算机博弈的研究也日趋深入[1]。除极大极小算法，Alpha-Beta搜索等传统搜索算法外，深度学习[2]和强化学习等机器学习相关算法[3]也已广泛地应用到计算机博弈当中。而藏棋“久”[4]是中国少数民族的棋种，于2019年加入到中国计算机博弈锦标赛当中。由于其所涵盖受众远小于围棋、国际象棋等常见棋种，因此国内外对久棋博弈策略的研究相对较少。针对这一现状，本文基于久棋两个博弈阶段规则和目的差异性大的特点，制定了一种分阶段的博弈策略：下子阶段，提出一种基于相对胜负的改进蒙特卡洛搜索算法[5];行期阶段，提出了一种加入过程分值的改进Alpha-Beta剪枝算法[6]。此外，根据下子阶段优先集中在中心区域及行棋阶段优先形成褡裢的估值策略，给出了一份完整的估值评估表。对此拟展开研究论述如下。

1藏族久棋规则

久棋的博弈全局分为下子和行棋两个阶段，下子阶段将棋子布满棋盘;行棋阶段通过移子来达到吃子的目的，最终获取胜利。对此可做阐释概述如下。

1.1下子和行棋规则

1.1.1下子和行棋方式

下子阶段为棋盘中央的格子用对角线相连接的点上作为对局双方下子的起始点，下子由白方先下，接着开始轮流下子布局，直至布满全局之后开始行棋。

行棋阶段开局如图1所示，行棋阶段中，先将棋盘中央方格的对角线两端的棋子去掉后开始行棋。因下子阶段由白方先下，为了对局双方公平，行棋则由黑方先行。在双方棋子个数均大于14颗时，行棋方式分为普通走子和跳子;在一方棋子个数小于14颗时，该方的行棋方式会新增飞子。飞子，即可以随意飞至棋盘上任意空位，不受正常行棋规则的约束。普通走子，即为棋子可以移至相邻空位。跳子分为单跳和连跳。单跳，就是相邻位为对方棋子时，该横（纵）方向第三点为空位，就可跳至该位，并跳吃中间对方棋子。连跳即为多步连续单跳。

1.1.2特殊棋形

（1）棋门：棋盘总共有196个格子，行棋时，棋盘正方形方格上的4个顶点都下某一方的棋子时，会形成一个最小正方形，这个正方形图案就称之为一个棋门。行棋是每形成一个棋门就可以吃掉对方任意一个棋子。棋门分为单棋门和双棋门。双棋门是2个单棋门连在一起形成。在行棋阶段，每形成一个双棋门，可以吃掉对方任意2个棋子。

（2）单褡裢：如果2个棋门之间有一个空格且有一颗棋子可以来回移动，并可以关闭两边的棋门。

（3）双褡裢：如果在2个棋门之间有一个空位，并来回移动一个棋子可以关闭2个棋门，可以吃对方任意2个棋子。单褡裢或双褡裢是保证行棋阶段提前获胜所需棋形的基本条件。

1.2吃子规则

（1）成方吃子：一方形成单棋门可以提掉对方任意位置一颗棋子，形成双棋门可以提掉2颗。

（2）跳子吃子：己方所落棋子的纵（横）线相邻的点上为对方的棋子，而第三点为空白点时，己方可以跳吃对方的棋子，依据情况选择单跳吃或连跳吃。

1.3胜负判别

在行棋阶段的胜负判别有2种。第一种为双方棋子个数均为14颗以上时，一方形成双褡裢且另一方不具有形成棋门的能力，此时形成双褡裢一方获胜;另一种为一方棋子减少至四颗以下，此时棋子少于4颗的一方判负。

2藏棋“久”的分阶段算法研究

藏族久棋分为下子阶段和行棋阶段，不同阶段的博弈目的和规则也具有较大的差别。其中，下子阶段是为行棋阶段谋篇布局，较好的布局能使行棋阶段开局己方占据主动性，能更有效地形成对己方有利的局面。行棋阶段则是通过行棋来吃掉对方棋子，破坏对方的特殊棋形，形成对己方有利的棋形，以获取最终的胜利。

考虑到该棋种两个阶段有较大差别，因此本文对一些博弈算法做出一定的改进，以便更适合该棋种。下子阶段，提出一种基于相对胜负的改进蒙特卡洛树搜索算法以获取最佳下子点;行棋阶段，提出一种加入过程分值的改进Alpha-Beta剪枝搜索算法，以便于各阶段尽可能获取最好的结果。

2.1下子算法

下子階段第一二步只能下在固定中心位置，其后便可下在任意点，但由于该棋盘为14×14规格，搜索空间过大[7]，若用Alpha-Beta剪枝搜索算法，搜索深度会过低，无法穷举计算出所有情况，进而导致给出的下子点效果不好。

下子阶段的久棋是可分出相对胜负，且具有确定性、顺序性和离散性的完全信息博弈。常规蒙特卡洛树搜索算法将当前局面作为根结点进行判断，然后进行选择，扩展，接着模拟到终端局面判断胜负情况，但考虑到久棋分为下子和行棋两个阶段，胜负判别在后一个阶段，因此本文提出在对局面双方进行整体评估统计分值后，通过得分情况判断相对胜负，赋予棋局不同状态对应分值，并对结点分值进行反向传播更新，以达到最终在限定时间内获取相对最优下子点的目的。

2.2行棋算法

行棋阶段开局时，可移动棋子主要集中在中心区域，初始可行棋点较少，搜索空间是在计算范围内的，可以有效模拟出所有可行点的行棋路径。

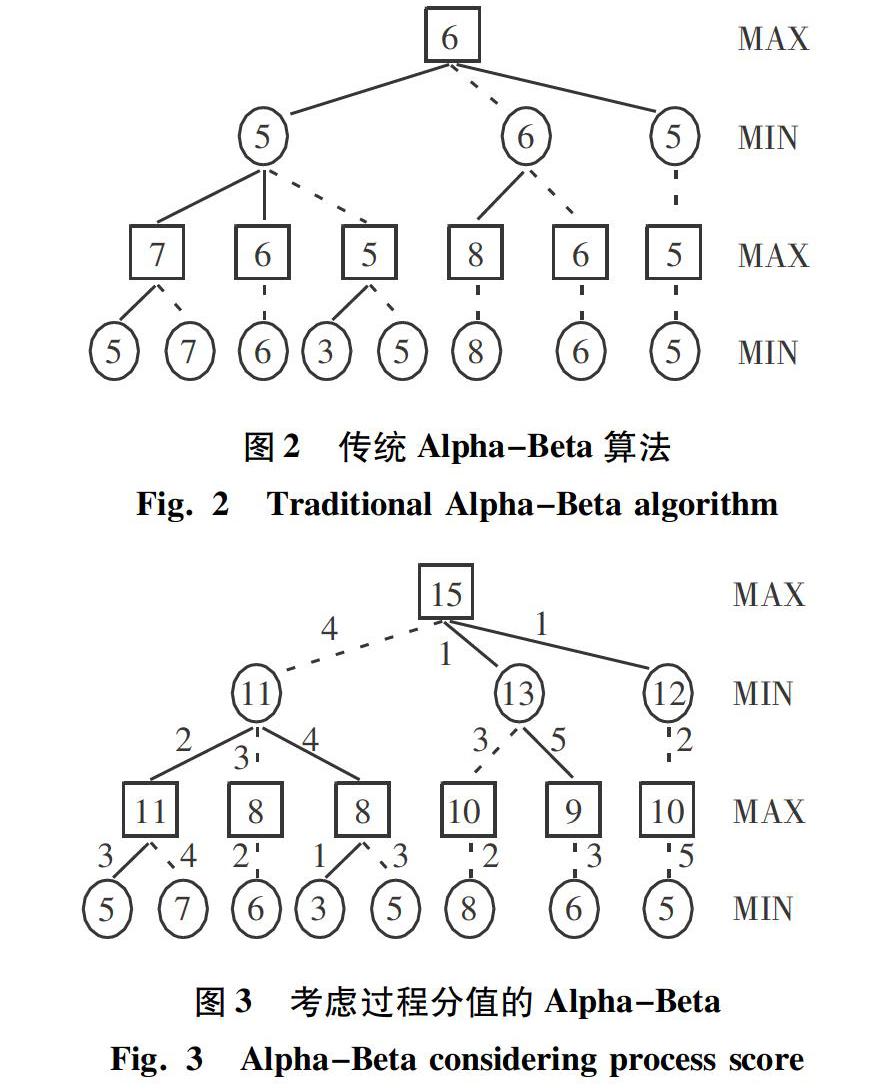
传统的Alpha-Beta剪枝搜索算法是在搜索到指定深度后，根据当前局面评估分值。传统Alpha-Beta算法如图2所示，图2中的虚线表示每一次选择的行棋路径，自下而上，依次比较选择，直至获取整个模拟过程中分值最高的行棋路径。

考虑到久棋在行棋阶段选择不同的行棋路径造成的吃子会对后续局面模拟造成一定影响，本文提出一种加入过程分值考量的Alpha-Beta剪枝搜索算法，如图3所示。图3中的虚线表示每一次比较选择的行棋路径，每一步行棋都会被赋予一个过程分值，到达指定搜索深度时，再由下至上反向进行局面得分统计并做出相应选择。与图2对比可以看出，在指定搜索深度局面相同分值的情况下，做出改进后的Alpha-Beta剪枝搜索算法与传统的每一步或最终选择的最优行棋路径都可能不同。因此加入了过程分值考量的Alpha-Beta剪枝搜索算法更加契合该棋种规则。

2.3评估策略

下子阶段，设置二连子、三连子、三角、成方，对角5种基础攻击棋形[8]，防止对方三角成方，防止对方三连子成双三角，防止对角成三角棋形3种基础防守棋形。在久棋博弈过程中，行棋是提取中心固定位置的双方棋子开局，中心区域的棋子初始的能动性较高，可进攻可防守。因此，若能在下子阶段尽可能地围绕中心区域展开布局，在行棋阶段开始则能有一定的主动性，可以把整局博弈的节奏掌握在己方手中，引导对局趋势朝利于己方的方向进行。

经过多次博弈实战，最终在蒙特卡洛树搜索算法模拟的结果得分和该棋子的位置得分之间获取了一个较好的比例平衡，对应数学公式可写为：

final_score=result_score×0.7+location_score×0.3.

（1）

其中，final_score表示最终评估得分;result_score表示模拟的结果得分;location_score表示棋子的位置得分。

行棋阶段中，有一个极为重要的攻防棋形—褡裢，形成单双褡裢会使一方在博弈对局中取得明显优势，既可以破坏对方成方及形成褡裢，也可以为己方成方及再次形成褡裢清除掉对方中有威胁的棋子。所以在其他基本棋形的基础上，新增褡裢的形成及破坏得分，同时新增吃子的得分，利用Alpha-Beta有效的搜索，选取己方分数最大的行棋路径。

2.4评估策略分值表

为了评判修改后的参数是否更优，本文采取机机博弈，即2个AI程序交替下棋直至分出胜负，通过控制变量法，将2个AI程序除了相应策略有关参数以外的所有函数均保持一致，通过蒙特卡洛树搜索算法计算出终端局面双方棋子的总分值，评判相对更优参数。下子阶段最终评估局面如图4所示，白子总分值高于黑子，此时白子的参数相对更好。接着修改评分较低一方的参数，模拟对局，直至出现比第一次较优参数更高的分值，以此来调试参数。

博弈策略分为2种，即：主进攻和主防守。其中，主进攻为优先形成自己的棋形，占据一定主动性，即己方形成一些基础棋形的分值会高于阻止对方形成相应棋形的分值。主防守则为优先阻止对方形成一些特定棋形，具有一定的被动性。在下子阶段形成褡裢会留空给对方棋子，以便提掉对方棋子后，中间可移动棋子可以来回成方，反复提取对方棋子，但若行棋阶段不能尽早成方提子，则该留空褡裢会被对方破坏，无法达到预期的效果，因此留空褡裢不宜贪多。此外，成方棋形灵活性较低，需多步才能制造优势，一般是为了形成褡裢的基础，因此尽可能优先形成基础棋形中可塑性最强的三角棋形。依据此策略，研究中还绘制了一份评估策略分值表，限于篇幅，此处不做赘述。

3实验结果与分析

3.1规则实现

3.1.1棋盘表示

久棋的棋盘有9路、11路、14路等，本文的算法研究均是在14路棋盘上展开。棋盘有纵横各十四条等距离，垂直交叉的平行线构成，形成196个交叉点，在藏棋中每个交叉点就是落子的地方，称为下子点。棋盘整体形状以及每个格子纵横向比相等。

本文采用14×14的二维矩阵抽象地表示各个下子点的下子状况，用1表示白子，用2表示黑子，用0表示下子点为空。

3.1.2跳吃实现

久棋行棋阶段的跳吃路径存储，纵向采取的数组形式，存储多个可行点;横向采取的单链表形式，存储多条可行路径。走子的存储是找到己方所有可行点，并在该点的上、下、左、右四个方位的相邻位置判断是否有空位，若有空位，即可直接记录起始点和终点坐标。

跳子分为单跳和连跳。单跳是通过判断己方所有棋子的相邻位置是否为对方棋子及第三点是否为空位，若是则可以单跳。连跳其实是一个不断将上一次单跳终点变为下一次单跳起始点的单跳过程，最终将整条行棋路径串连，即为完整连跳路径。获取所有点可行跳吃路径步骤可分述如下：

（1）调用JumpMoveList函数对不同位置的己方点进行遍历，且相邻点为对方棋子，单跳到达点为无子情况。

（2）判断横纵四个方向的状况，判断某点是否存在可单跳的情况。

（3）若存在单跳，调用hop函数判断单跳的终点是否可以连跳;若不存在，则退出跳子行棋方式判断。

（4）递归调用jump函数不断地将不同方向的连跳情况存入在内。

（5）当某条跳子路径到达尽头时，调用jumpback函数回溯，恢复初始状态。

（6）重复（2）～（5），判断上一阶段某点的其余方向存在跳子可能的情况，直至找到所有可行点的可行路径。

其中，hop函数是判断某点能否连跳;jumpback函数是回溯到棋局初始状态;jumpMoveList函数是获取单跳路径;jump函数是递归查找所有连跳方法。

综上可得，连跳前的棋局如图5所示，连跳后的棋局如图6所示，单跳成方吃子前棋局如图7所示，单跳成方吃子后棋局如图8所示。

3.1.3褡裢的判断

褡裢是久棋中十分重要的棋形，分为单褡裢和双褡裢。在博弈过程中，许多进攻和防守的操作都是通过褡裢完成的。分析可知，褡裢的特点就在于，每移动一次褡裢中间的棋子，至少可以提掉对方一颗棋子，极具主动性。

单褡裢以不同的形式遍布在一个3×4（或竖置）的格局内，由于单褡裢样式一定，因此本文采用枚举的方法，搭建一个单褡裢库，再与所有符合情况的单褡裢进行匹配，给予不同的标号标识，并记录单褡裢中可移动棋子的位置，便于后续评估函数制定分值比重。而双褡裢是基于单褡裢的复杂棋形，可通过单褡裢的特殊叠加方式判别。

在整个棋盘中，遍历每一个3×4的矩形区域，首先判断其是否为一个褡裢，如果不是则排除;如果是，就记录该矩形左上角点的坐标，用于记录这个褡裢在整个棋盘中的位置。通过遍历整个棋盘一次，可以查询出所有横置褡裢的位置，接着将棋盘数组转置，再进行一次前述的遍历操作，就可查询出所有竖置的褡裢。在此基础上，将所有的褡裢位置用链表存储，用于后续的评估操作。

3.2算法实现

本文首先定义一个结点类，其属性有chessmans，rewardMap，accessNumber，nextNode等，chessmans表示该结点的棋盘状态，在进行选择的时候，默认优先选择未被扩展的结点，即棋盘上显示为0的点（利用Node的nextNode属性，该属性为一个Node二维数组，大小为14×14，Node.nextNode[i][j]=null就表示其未被扩展），当该结点的所有子结点都已被选择遍历，利用getBestChild，通过公式（2）计算该节点UCB值：

4结束语

本文对藏棋“久”进行分阶段算法研究，在下子阶段，提出一种基于相对胜负的改进蒙特卡洛树搜索算法，在限定下子时间内获取相对最优下子点;在行棋阶段，提出一种加入过程分值的改进Alpha-Beta剪枝搜索算法，并给出一份完整的估值评估表。通过与技术较高的棋手博弈，测试发现通过上述算法及估值表实现的AI博弈引擎具有较强的棋力。

虽然本文提到了一些较好的设计思想，但因为一些不可控因素，具体功能在实现上还有待进一步完善。如该棋种规则相对复杂，涉及吃子、特殊棋形及多种着子方式，因此普通的传统算法若没有良好的评估函数和剪枝条件，就会进行大量无用的搜索，甚至会剪去较好的局面，造成搜索深度过低且棋力不足等后果，接下来的研究会优化评估函数和剪枝条件。此外，Alpha-Beta搜索的层数过低，算法以及数据结构还需再进行深入优化，动态控制搜索深度。MCTS搜索的结点过少，数据结构还需做进一步优化，考虑的因素需要做适当的增删。

参考文献

[1]张芃芃，孟坤，杨震栋.基于强化学习的海克斯棋博弈算法研究与实现[J].智能计算机与应用，2020，10（3）：142-145.

[2]LECUNY，BENGIOY，HINTONG.Deeplearning[J].Nature：InternationalWeeklyJournalofScience，2015，521（7553）：436.

[3]周志华.机器学习[J].北京：清华大学出版社，2016.

[4]中国大学生计算机博弈大赛组委会.久棋规则及棋谱简介[EB/OL].[2019-04-29].http：//computergames.caai.cn/info/news190429.html.

[5]CHASLOTG，BAKKESS，SZITAI，etal.Monte-Carlotreesearch：AnewframeworkforgameAI[C]//ArtificialIntelligence&InteractiveDigitalEntertainmentConference.PaloAlto，California：DBLP，2008：216-217.

[6]PEARLJ.Thesolutionforthebranchingfactorofthealpha-betapruningalgorithmanditsoptimality[J].CommunicationsoftheACM，1982，25（8）：559.

[7]王松.久棋強化学习博弈研究及多媒体课件开发[D].北京：中央民族大学，2019.

[8]李霞丽，吴立成，李永集.基于棋型的藏族“久”棋计算机博弈研究[J].智能系统学报，2018，13（4）：577-583.