基于有向无环图的区间覆盖率求解算法
杜明 庞建成 周军锋
摘 要:给定一个有向无环图,回答可达性查询是图的基本操作之一。虽然很多方法使用树区间来加速可达查询的处理速度,但并不明确使用多少个区间比较合适。本文提出一种快速计算区间覆盖率的算法,该方法通过使用有效的剪枝策略来支持高效的覆盖率计算。基于所得到的区间覆盖率,可针对不同数据图确定合适的区间个数,以便在加速查询处理的同时,降低索引规模。基于多个真实数据集的实验验证了本文提出方法的高效性。
关键词:有向无环图;可达性查询处理;区间覆盖率
【Abstract】Givenadirectedacyclicgraph,answeringthereachabilityqueryisoneofthebasicoperationsofthegraph.Althoughmanymethodsusetreeintervalstospeeduptheprocessingspeedofreachablequeries,itisnotclearhowmanyintervalsareappropriate.Thispaperproposesanalgorithmtoquicklycalculatethecoverageofmultipleintervals.Thismethodsupportsefficientcoveragecalculationbyusinganeffectivepruningstrategy.Basedontheobtainedintervalcoverage,anappropriatenumberofintervalscanbedeterminedfordifferentdatagraphs,soastoreducetheindexscalewhilespeedingupqueryprocessing.Experimentsbasedonmultiplerealdatasetsverifytheefficiencyofthemethodproposedinthispaper.
【Keywords】directedacyclicgraph;reachabilityqueriesprocessing;intervalcoverage
作者簡介: 杜 明(1975-),男,博士,副教授,主要研究方向:自然语言处理、信息查询、数据分析;庞建成(1995-),男,硕士研究生,主要研究方向:图的可达查询覆盖率研究;周军锋(1977-),男,博士,教授,博士生导师,主要研究方向:大图数据的查询处理技术、推荐系统关键技术。
0 引 言
给定有向无环图(DirectedAcyclicGraph,DAG),以及图中任意两个顶点u、v,可达性查询u?→v用于回答从顶点u出发是否存在一条路径可以到达顶点v。可达性查询处理是图数据管理与分析的基本操作之一,一直以来都是研究者广泛关注的热点问题[1-10]。在实际应用中,可达性查询被广泛应用到社交网络、通信与传感器网络、生物网络、可扩展标记语言数据、资源描述框架数据等领域,用于检测两点间是否存在特定关系。
虽然使用多个区间可以回答更多的可达性查询,但是现在的方法并不明确使用多少个区间比较合适。一方面,使用多个区间可以扩大覆盖率,从而增强区间标签的剪枝能力;另一方面,使用多个区间也意味着较大的索引和较长的查询响应时间。因此使用区间标签来加速可达查询处理时,一个关键问题是:应该建立多少个区间标签,从而在查询时间、索引大小以及索引构建时间之间获得平衡。显然,该问题的解决依赖于高效获知区间标签的覆盖率,如此即可根据系统的硬件环境限制,选择合适的区间个数,进而加速查询响应的效率。
然而,覆盖率的计算并非易事,原因在于不同生成树区间所覆盖的后代顶点有重复,多个区间覆盖率并非简单的累加和,需要在计算过程中去除重复部分。针对该问题,本文首次提出一种快速计算区间覆盖率的算法,称k-DFSIC(k-DepthFirstSearchIntervalCoverage),其中k表示生成树区间的个数。该方法在求解覆盖率时通过使用有效的剪枝策略来支持高效的覆盖率计算,基于所得到的区间覆盖率,用户可针对不同数据图确定合适的区间个数来获得最佳的性能体验。
本文的其余部分安排如下。第1节介绍相关工作,第2节提出求区间覆盖率的算法,第3节展示实验结果,第4节总结全文。
1 相关工作
1.1 问题定义
虽然可达性查询针对的是一般有向图,但是现有方法可以通过压缩其中的强连通分量将其转换为有向无环图来处理,因此,本文假设输入的都是有向无环图。以下介绍区间覆盖率的定义及问题的定义。
定义1 区间覆盖率 给定有向无环图及其生成树上的多个区间,区间覆盖率表示仅通过顶点的区间能回答的可达对个数占有向无环图中所有可达对个数的比例。
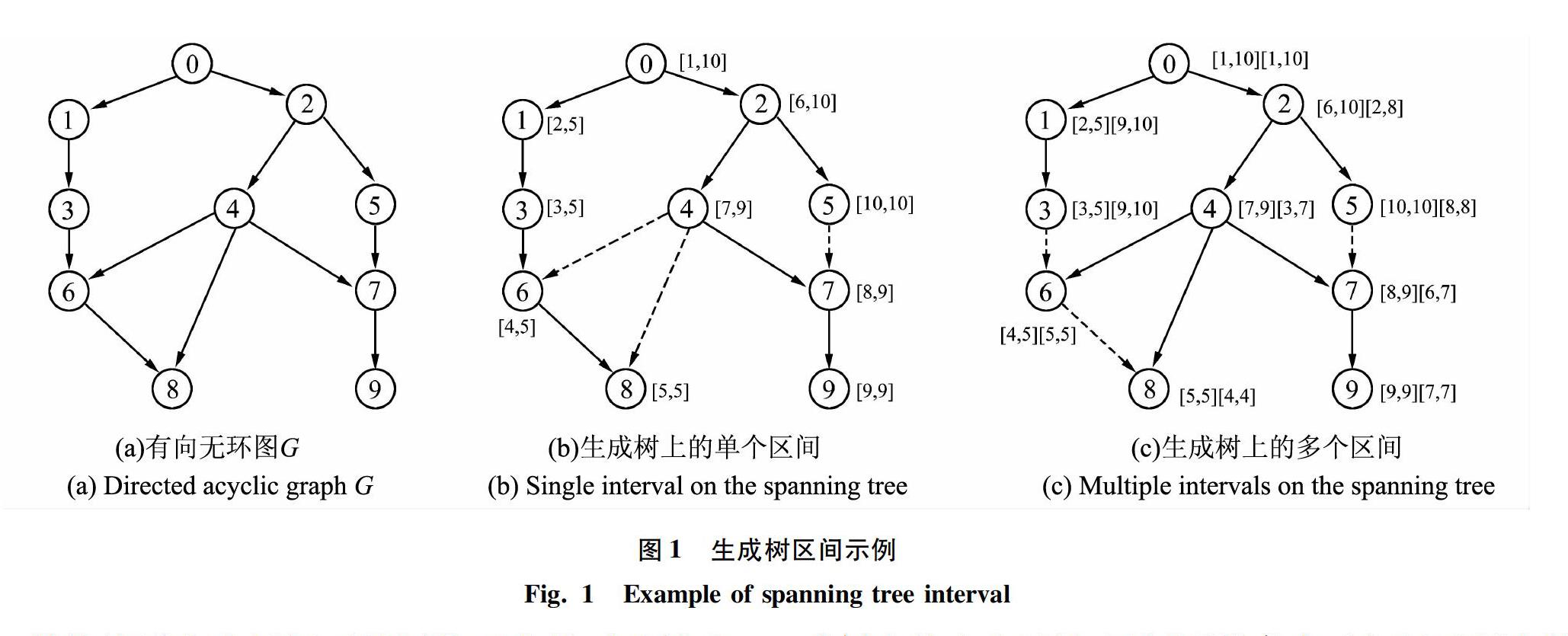
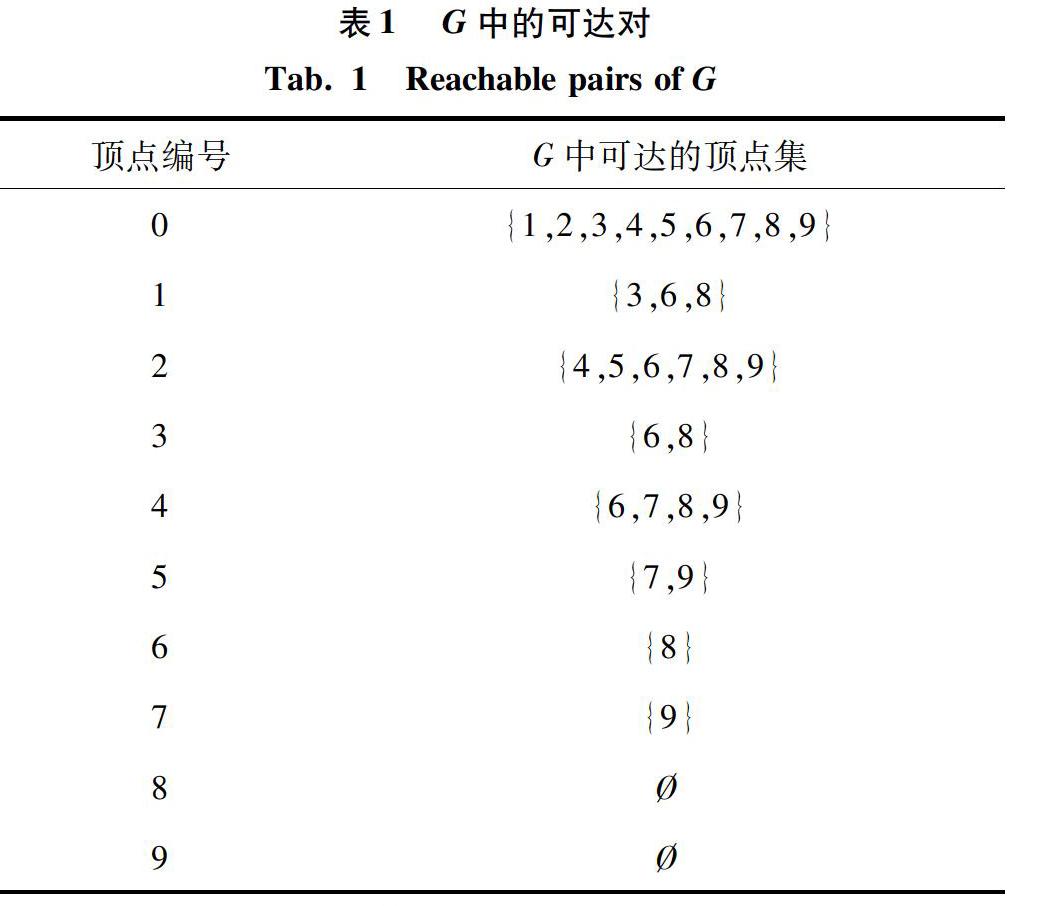
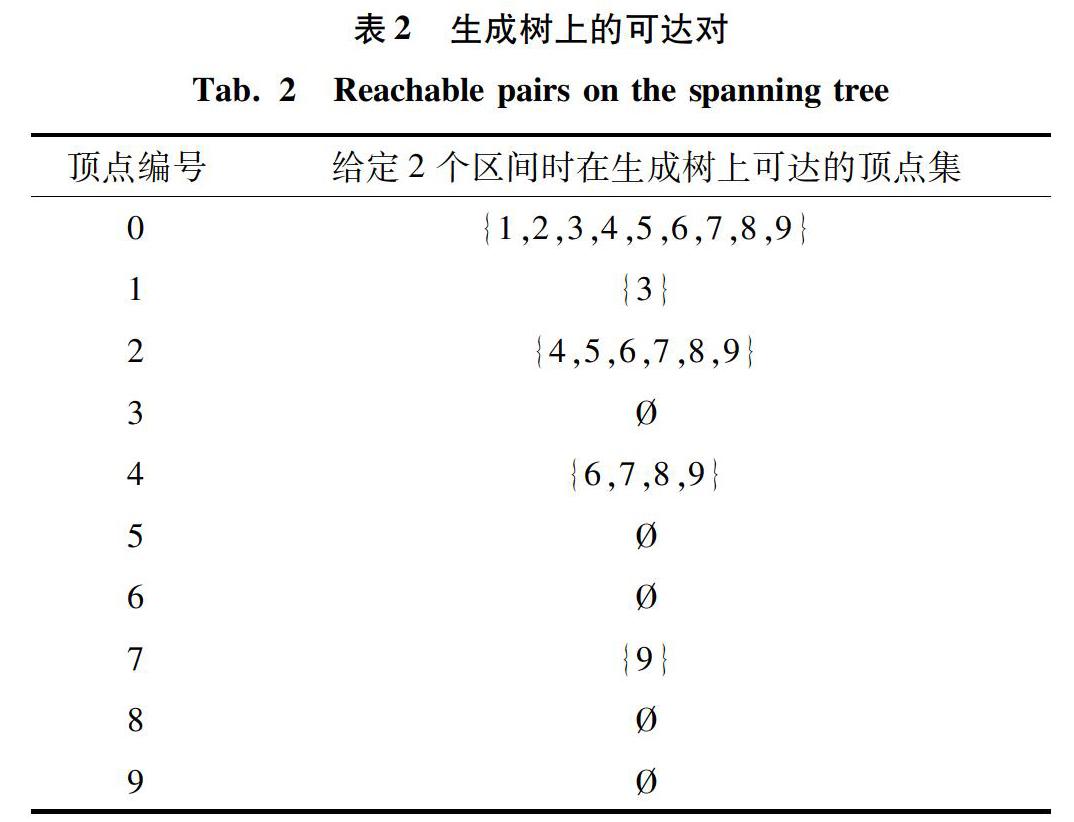
例如图1(a)中有向无环图G的所有可达对的数目为28,图1(b)中所用一个生成树区间能够回答的可达对个数是22个,则使用一个区间时,其区间覆盖率为22/28,图1(c)中使用2个生成树区间能够回答的可达对个数是26个,则其区间覆盖率为26/28。
问题定义: 给定有向无环图及其对应的多个生成树区间,返回这些生成树的区间覆盖率。
1.2 相关算法
虽然区间覆盖率可用于协助用户针对不同图来确定合适的区间个数,但关于区间覆盖率的计算问题还未见到任何研究,本文首次对区间覆盖率的问题进行研究,提出一种快速计算区间覆盖率的算法。这里,研究中仅讨论使用区间的可达性查询处理算法,包括GRAIL[11]、FERRARI[5]、FELINE[12]三个算法。对此可做阐释分述如下。
GRAIL算法基于生成树为每个点附加多个区间,其中一半区间是包含所有图中后代的区间,用于判断不可达,另外一半区间是包含生成树中后代的区间,用于判断可达。由于区间个数会影响索引大小及查询效率,本次研究在进行实验时,基于数据图的稀疏程度来设定区间个数。对于稀疏图(度小于2),使用2个区间,其它图使用5个区间。该方法是一种基于经验的直觉,区间增多时,不一定能增强查询处理能力。
FELINE用x和y表示顶点的2个拓扑号,用I表示顶点的区间标记。在判断顶点u是否可达顶点v的时候,如果顶点的拓扑号满足xu>xv或者yu>yv,则可知顶点u不可达顶点v;如果xu FERRARI根据内存的限制情况来确定区间个数,由于区间之间有重叠,因此即使内存够大,可支持多个区间,但却仍然难以保证查询效率。 以上方法虽然都使用区间来加快可达性查询的处理效率,但是这些方法都不能确定应该使用多少区间来回答才合适,针对该问题,本文提出一种快速计算区间覆盖率的方法,以便针对不同数据图确定合适的区间个数,从而提升查询效率并减小索引规模。 2 求区间覆盖率的算法 2.1 基础算法 给定有向无环图G及其生成树上的k个区间,求区间覆盖率的基本思想是:首先找到图G中所有的可达对;然后判断这些可达对是否能通过区间回答,能回答说明该可达对能够通过区间判断,不能回答则说明该可达对不能通过区间判断;最后求出可以通过区间回答的可达对个数占图G中所有可达对个数的比例,即可得到使用k个生成树区间的覆盖率。 算法1展示了基础算法求区间覆盖率的伪代码,具体如下。 算法中,第1行设置2个变量nRch和nUnRch,分别表示可以通过生成树区间回答的可达对个数和不能通过生成树区间回答的可达对个数,并将其初始值设为0;第2~7行针对图G中所有的可达对,依次判断其是否能通过给定的k个区间回答,如果可以回答,nRch++,如果不能回答,则nUnRch++;第8行通过nRch的值除以(nRch+nUnRch)的值求出使用k个生成树区间的覆盖率。 给定有向无环图G见图1(a)。首先找到图G中所有的可达对,详见表1,总共有28个;然后判断这些可达对能否通过给定的区间回答。研究可知,图1(b)为图G中每个节点给定了一个生成树区间,[8,9](v7的区间)[7,9](v4的区间),说明v4→v7可以通过该区间回答,则通過一个区间能回答的可达对个数nRch++,而[4,5](v6的区间)[7,9](v4的区间),说明v4→v6不能通过该区间回答,则不能通过一个区间回答的可达对个数nUnRch++,当图G中所有可达对判断结束后,可以得到nRch为22,nUnRch为6,故通过计算可得使用一个区间的覆盖率是22/(22+6),即22/28。研究中的图1(c)又为G中每个节点给定了2个生成树区间,[5,5](v6的第二个区间)[3,7](v4的第二个区间),说明v4→v6可以通过该区间回答,则通过2个区间能回答的可达对个数nRch++,而[6,7](v7的第二个区间)[8,8](v5的第二个区间),说明v5→v7不能通过该区间回答,则通过2个区间不能回答的可达对个数nUnRch++;当图G中所有可达对判断结束之后,可得nRch为26,nUnRch为2,则通过计算可得使用2个区间的覆盖率是26/(26+2),即26/28。 基础算法若要枚举有向无环图G中所有的可达对,需要的时间为O(kn(n+m)),其中n为G的顶点个数,m为G的边数。判断每个可达对能否通过生成树区间回答,可以在O(k)时间内完成,故基础算法的时间复杂度是O(kn(n+m))。 2.2 k-DFSIC算法 由于基础算法在计算过程中需要枚举有向无环图中所有的可达对,时间复杂度太大,在实践中无法处理大图。针对该问题,本文提出一种快速计算区间覆盖率的k-DFSIC算法。给定有向无环图G及其k个生成树区间,求区间覆盖率之前,为图中每个节点设定一个计数器,表示该节点通过区间能回答的可达对个数,初始值为第一个区间的长度。求区间覆盖率的基本思想是:当求解顶点u的第i个区间新增的可达查询数量时,对于第i个区间中的所有生成树后代点,即检视u与其之间的可达性是否可以通过前i-1个区间来判断。如果可以,则u的计数器不变,否则说明该可达对无法通过前i-1个区间判断,则u的计数器加1。当所有顶点处理结束后,将顶点的计数器累加,即可得到所有节点通过区间能回答的可达对个数。该值除以图G中所有可达对个数,就是使用k个区间的覆盖率。 算法2展示了k-DFSIC算法求区间覆盖率的伪代码,具体如下。 算法中,第1行设置了一个变量nTC表示有向无环图G的传递闭包的大小;第2行设置了一个变量nRCH表示图G中所有节点通过区间能回答的可达对个数,并设其初始值为0;第3行为图G中每个节点u给定一个计数器表示该节点通过区间能回答的可达对个数nRch,其初始值为节点u的第一个区间长度;第4~12行在求解节点u通过i(2≤i≤k)个区间新增的可达查询数量时,对于第i个区间中的所有生成树上后代节点v,设置一个变量flag表示u和v之间的可达性是否可以通过前i-1个区间来判断,其初始值设为TRUE,如果u和v之间的可达性可以通过前i-1个区间来判断,则flag值为FALSE,判断后如果flag值为TRUE,说明该可达对无法通过前i-1个区间判断,则nRch加1;第13~14行将图G中每个节点的计数器nRch加和即所有节点通过区间能回答的可达对个数nRCH,用nRCH的值除以图G中所有可达对的个数nTC,即可得到使用k个区间的覆盖率。 例如,图1(a)所示有向无环图G中所有可达对共有28个,参见表1,即图G的传递闭包的大小nTC为28。 由图1(b)可知,为图G中每个节点给定了一个区间,并为每个节点给定一个计数器表示该节点通过一个区间能回答的可达对个数nRch为该节点的区间长度,比如说v4的区间是[7,9],则v4通过一个区间能回答的可达对个数nRch为v4的区间长度2,将每个节点的nRch值加和可以得到所有节点通过一个区间能回答的可达对个数nRCH为22,则使用一个区间的覆盖率是22/28。 由图1(c)可知,为图G中每个节点给定了2个区间,并为每个节点给定一个计数器表示该节点通过2个区间能回答的可达对个数nRch首先设置为该节点的第一个区间的长度,对于生成树上每个节点来说,要找到该节点到其后代节点的所有可达查询,参见表2,并检查这些查询能否通过前i-1个区间回答来更新nRch的值,比如v4节点,v4的第一个区间是[7,9],则v4通过2个区间能回答的可达对个数nRch首先设置为v4的第一个区间的长度2,然后依次检查v4→v6,v4→v7,v4→v8,v4→v9能否通过前i-1个区间回答来更新nRch的值,可以发现v4→v6不可以通过第一个区间回答,但是可以通过第二个区间回答,则nRch++,同理v4→v8也不可以通过第一个区间回答,但是可以通过第二个区间回答,则nRch++,而v4→v7,v4→v9已经可以通过第一个区间回答了,则nRch值不变,当所有查询判断结束之后,可以得到v4通过2个区间能回答的可达对个数nRch为4;将每个节点的nRch值加和可以得到所有节点通过2个区间能回答的可达对个数nRCH为26,则使用2个区间的覆盖率是26/28。 k-DFSIC算法需要在有向无环图G上找到其生成树上的每个节点的后代节点。和基础算法不同,基础算法需要枚举图上的后代,而k-DFSIC只需要枚举树上的后代,该值等于树上每个顶点的高度之和。假设顶点的平均高度是h,则求解可达对个数nRCH的代价是O(k(n+m)+khn),其中n为G的顶点个数,m为G的边数;同时,求传递闭包的时间代价为O(wm)[13],这里w是求传递闭包大小过程中,处理每个点时平均处理代价。因此,k-DFSIC的时间复杂度是O(k(n+m)+khn+wm)。 3 实验分析 3.1 实验环境 实验所用的硬件平台是IntelCorei5-4460主频为3.20GHz的CPU,4GB的RAM内存,操作系统为Ubuntu8.3.0,并使用gcc8.3.0进行编译,以上算法均采用C++语言实现。 3.2 数据集 本文中使用的12个数据集见表3。这些数据集都广泛地出现在图的可达查询研究中[4-5,9,14-16],这些数据集都是有向无环图,表3中标注了每個数据集的顶点数|V|以及边数|E|。 3.3 索引大小 k-DFSIC算法求区间覆盖率使用不同区间时的索引大小见表4。由表4可以看出随着区间个数的增加,索引大小呈线性增加。 3.4 覆盖率求解时间 表5比较了基础算法和k-DFSIC算法求区间覆盖率所需的时间。由表5可以发现k-DFSIC算法与基础算法相比,在使用相同区间个数的情况下,所需的时间要少得多,并且基础算法在大图当中运行时间太长,而k-DFSIC算法则只需很少的时间,表5中,“-”表示基础算法运行时间超过了2h。 3.5 区间覆盖率 表6展示了本文实验所得到的区间覆盖率。由表6发现随着区间个数的不断增加,覆盖率虽然也不断增加,但是有的数据集覆盖率增加值比较小,比如twitter数据集;而有的数据集覆盖率增加值比较大,比如xmark数据集,使用5个区间时的覆盖率是使用1个区间时覆盖率的3倍多。 3.6 实验结论 首先,本文提出的区间覆盖率计算算法可高效求解区间覆盖率,在实际中需要了解区间覆盖率的情况下,可通过使用本文提出的算法进行高效求解;其次,通过本文实验所得到的区间覆盖率,可以发现有些数据集只需要使用2个区间来回答可达性查询就比较合适了,比如human数据集,而有的数据集使用5个区间比较合适,比如xmark数据集。假设内存足够的情况下,考虑到查询效率,针对不同数据集回答可达性查询合适的区间个数见表7;如果内存不足以使用多个区间,则需要用户根据实际情况确定合适的区间个数。 4 结束语 本文针对已有算法回答可达性查询时使用树区间来加快处理速度、但是并不明确使用多少个区间比较合适的问题,首次提出了一种快速计算区间覆盖率的算法。实验结果表明,本文提出的算法可高效计算区间覆盖率。基于所得到的区间覆盖率,用户可结合实际应用环境的限制确定可达查询处理过程中应该使用的区间数量,从而获得最佳的性能体验。 参考文献 [1] AGRAWALR,BORGIDAA,JAGADISHHV,etal.Efficientmanagementoftransitiverelationshipsinlargedataandknowledgebases[J].ACMSIGMODRecord,1989,18(2):253-262. [2]CHENGJ,HUANGS,WUH,etal.TF-Label:Atopological-foldinglabelingschemeforreachabilityqueryinginalargegraph[C]//Proceedingsofthe2013ACMSIGMODInternationalConferenceonManagementofData.NewYork,USA:ACM,2013:193-204. [3] JINR,WANGG.Simple,fast,andscalablereachabilityOracle[J].VeryLargeDataBases,2014,6(14):1978-1989. [4]JINRuoming,XIANGYang,RUANNing,etal.Efficientlyansweringreachabilityqueriesonverylargedirectedgraphs[C]//Proceedingsofthe2013ACMSIGMODInternationalConferenceonManagementofData.Vancouver,BC,Canada:ACM,2008:595-608. [5]YILDIRIMH,CHAOJIV,ZAKIMJ.GRAIL:Ascalableindexforreachabilityqueriesinverylargegraphs[J].TheVLDBJournal,2012,21(4):509-534. [6]ZHANGTianming,GAOYunjun,LICongzheng,etal.Distributedreachabilityqueriesonmassivegraphs[M]//LIG,YANGJ,GAMAJ,etal.DatabaseSystemsforAdvancedApplications.DASFAA2019.LectureNotesinComputerScience.Cham:Springer,2019,11448:406-410. [7]SENGUPTAN,BAGCHIA,RAMANATHM,etal.ARROW:ApproximatingreachabilityusingrandomwalksoverWeb-scalegraphs[C]//InternationalConferenceonDataEngineering.Macao,China:dblp,2019:470-481. [8]BENDERMA,FINEMANJT,GILBERTS,etal.Anewapproachtoincrementaltopologicalordering[C]//SymposiumonDiscreteAlgorithms.Austin,Texas:dblp,2009:1108-1115. [9]JAGADISHHV.Acompressiontechniquetomaterializetransitiveclosure[J].ACMTransactionsonDatabaseSystems,1990,15(4):558-598. [10] CHENY,CHENY.AnEfficientalgorithmforansweringgraphreachabilityqueries[C]//IEEE24thInternationalConferenceonDataEngineering.Paris,France:IEEE,2008:893-902. [11] YILDIRIMH,CHAOJIV,ZAKIMJ.Grail:Scalablereachabilityindexforlargegraphs[J].ProceedingsoftheVLDBEndowment,2010,3(12):276-284. [12] VELOSORR,CERFL,JrMEIRAW,etal.Reachabilityqueriesinverylargegraphs:Afastrefinedonlinesearchapproach[C]//17thInternationalConferenceonExtendingDatabaseTechnology.Athens,Greece:dblp,2014:511-522. [13] TANGXian,CHENZiyang,LIKai,etal.Efficientcomputationofthetransitiveclosuresize[J].Clust.Comput.,2019,22(Supplement):6517-6527. [14] JINR,RUANR,DEYS,etal.SCARAB:Scalingreachabilitycomputationonlargegraphs[C]//Proceedingsofthe2012ACMSIGMODInternationalConferenceonManagementofData.Scottsdale:ACM,2012:169-180. [15] CHAM,HADDADIH,BENEVENUTOF,etal.MeasuringuserinfluenceinTwitter:Themillionfollowerfallacy[C]//ProceedingsoftheFourthInternationalConferenceonWeblogsandSocialMedia(ICWSM2010).Washington,DC,USA:dblp,2010:10-17. [16] VanSCHAIKSJ,DeMOORO.Amemoryefficientreachabilitydatastructurethroughbitvectorcompression[C]//Proceedingsofthe2011ACMSIGMODInternationalConferenceonManagementofData.Athens,Greece:ACM,2011:913-924.

