基于ANTs配准的多图谱分割算法比较研究

江 妍，马 瑜，芦 玥，王 原，梁远哲，李 霞

(宁夏大学 物理与电子电气工程学院,宁夏 银川 750021)

1 引 言

近年来，脑部疾病的发病率越来越高，时刻威胁着人们的健康和生命，人脑中的海马体一旦被破坏，就会出现如精神分裂症和抑郁症等脑部疾病。然而，海马体的结构体积在人脑MR图像中占有相对较小的空间，它的形状和拓扑结构本身也较为复杂，会导致人脑磁共振(Magnetic Resonance,MR)图像中海马体结构的边界不清晰。因此，从人脑中更精确地提取出海马体，会更有助于海马体体积的测量以及对其形态的分析，对脑部疾病的诊断治疗有重大的意义。

人脑MR图像是由大脑磁共振成像(Magnetic Resonance Imaging,MRI)的灰度图像和其相对应的大脑MRI的标记图像(标签图像)组成的。它们在空间位置上是一一对应的，人体大脑MRI的灰度图像可以显示脑部组织结构，标记图像用不同的颜色对人体大脑MRI的灰度图像中各个结构进行标记。

计算机断层扫描(Computed Tomography,CT)和磁共振成像(Magnetic Resonance Imaging,MRI)算法可以有效提高影像质量，从而可以高效精确地进行CT或MRI的分割任务。由于低剂量计算机断层扫描(Low-dose computed tomography,LDCT)图像经常被放大的斑驳噪声和条纹伪影严重退化，Chen[1]等人在2014年提出了伪影抑制字典学习(Artifact Suppressed Dictionary Learning,ASDL)”来处理LDCT图像，该方法可以有效地应用于最新的CT系统。Yin[2]等人在2019年提出了一种用于LDCT的域渐进三维剩余卷积网络(Domain Progressive 3D Residual Convolution Network，DP-ResNet)，该网络可提高低剂量CT成像。吴磊[3]等人提出了一种应用于CT图像的多尺度残差网络模型。陈雯艳[4]在2012年提出基于感兴趣区域多图谱配准的海马体分割算法，得到最终的分割结果。但该算法运行时间过长，分割结果与金标准相比仍存在差距。Chen[5]等人在2008年提出了一种新的非局部先验来计算每个像素在更广泛的邻域上的差异，其权重取决于像素相对于其他像素的相似性。Joshi[6]等人利用图谱的先验知识，提出基于多图谱的配准方法，但该方法得到的结果图精度不高且仍有错误标记的图谱出现。

针对以上问题，对于人脑MRI海马体分割，本文提出利用ANTs系统中的一组算法:刚性算法、仿射算法、对称图像归一化(Symmetric Image Normalization,SyN)算法来代替重采样环节以实现最优配准，并且在融合阶段，比较分析了4种融合算法的精度和效率。从实验结果可知，基于ANTs配准并结合半监督随机森林融合算法后，可明显改善传统分割算法中精度低、效率慢的问题。

2 传统多图谱海马体分割算法

2.1 预处理

在人脑磁共振图像中，非脑组织占很大比重，它会影响实验的精度，因此在图像配准前，需要对原始的脑部MR图像进行颅骨剥离，本文采用的是Stefan Bauer[7]提出的大脑表面提取(Brain Surface Extractor,BSE)算法。为有良好的分割效果，本文利用包围盒算法从两个图像库中分别以大小为60×74×67和50×50×50提取图像感兴趣区域(Region of Interest,ROI)。本文图库2以灰度图a11、标记图a11-seg为参考图像，对图谱进行以参考图像为基准的重采样操作。参考图像的尺寸大小、体素间距和图像中心分别为176×198×160，1×1×1，(90.89，92.29，79.18)。例如，当图谱a06的尺寸大小、体素间距、图像中心分别为176×198×160,1×1×1,(81.99,92.29,74.49)时，则重采样后灰度图像a04具有和参考图像一样的大小、间距和图像中心，能够有效减少图谱配准运行时间，改善配准的精度。

MAIS中,Aljabar[8]等人在研究中发现,磁共振成像的分割精度并不随图谱数量的增多而提高。典型MAS算法的计算时间是与图谱的数量线性相关的，因此从大量的图谱中选择合适的图谱子集可有效提高算法速度，提高最终分割准确性。本文采用归一化互信息(Normalized Mutual Information,NMI)进行待分割MRI与其他MRI的相似性计算，选择与目标图像最相似的图谱作为最终的融合图谱。Awated[9]等人2012年的研究表明，选择图谱的最佳数量为10个左右，因此本文从两个图库中均选择10幅最佳图谱。

NMI源于信息熵的概念，用来度量两个变量之间相互关联的程度[10]。运用NMI来度量3D感兴趣区域的相似度，其公式如下：

NMI(x,y)=(H(x)+H(y))/H(x,y)，

(1)

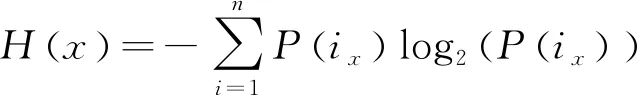
(2)

(3)

其中，x、y分别表示两幅 MR 图像，ix、iy分别表示x与y的像素值，n为总像素个数。计算出NMI的值越大则说明图谱图像与目标图像越接近，即相似性越高；反之，计算出NMI的值越小，则说明图谱图像与目标图像的相似性越低。

2.2 传统的多图谱海马体分割配准算法

图像配准与图像融合是医学图像多图谱分割算法的两个关键环节。精确的配准结果使得形变后的图谱图像对应的标记图像与待分割图像中的海马体在形状、体积、大小方面更相似[11]。

图像的全局粗配准采用的是刚性配准方法。该方法主要是基本的方向或者角度配准，没有任何形变。重采样是基于灰度的图像配准，它与全局粗配准有一样的效果。对于目标图像与图谱图像的大小、中心不一致的问题，可采用重采样方法，该方法可为后续非刚性配准提供了良好基础[12]。微分同胚是可逆的光滑映射，微分同胚Demons算法[13]，结合了Demons算法和李群的映射方法与最优化方法，能较好地实现图像配准效果。

3 基于ANTs配准的多图谱分割算法

3.1 高级标准化ANTs配准

ANTs(Advanced Normalization Tools)是美国宾夕法尼亚大学PICSL实验室基于图像分析工具库(Insight Segmentation and Registration Toolkit,ITK)开发的大脑图像配准的工具包[14]，是目前配准质量最好的软件，运行速度很快。ANTs安装适用于Linux和Mac,本文是在Linux系统中采用源码安装的。

ANTs配准的一般应用有两种。第一个应用程序将标记数据从模板图像空间转换为单独的空间。该应用很重要，当外观本身不足以定位一个结构时，将多个模板映射到单个模板(多模板标记)可以进一步提高准确性[14-15]。第二个应用程序按照与第一个应用程序相反的方向运行，将个体映射到模板。ANTs工具包支持这两种映射，它使用物理空间来定义映射。我们可以使用PrintHeader来检查数据，并在运行大量数据之前运行简单、快速的测试(很少的迭代)来执行完备性检查。此外，ANTs变形由标准命名前缀和标准命名扩展组成，通常使用.nii格式。

本文用ANTs代替重采样环节，在ANTs中使用一组算法：刚性算法、仿射算法和SyN算法，该组算法中包含微分同胚(Diffeomorphic)、弹性(Elastic transformation)和B样条(Bspline)等形变模型，同时也有互信息、相关系数等多种相似度测量，还可以优化策略。

.

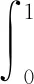
(4)

本文采用的是图像处理软件包ANTs所包含的Geodesic-SyN配准算法。Geodesic-SyN算法使用双向梯度下降优化，使用该算法可得到两个对称的映射，同时也可以把速度场分成两个，如公式(5)所示：

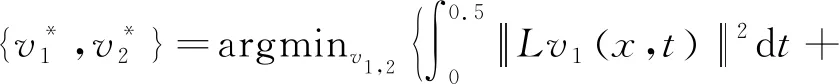
(5)

根据双流向的梯度下降法，更新算法公式如下：

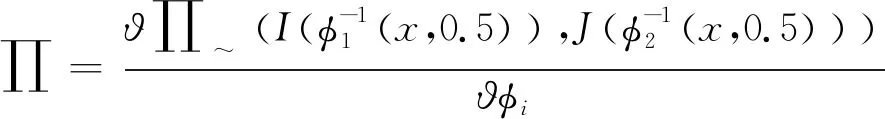
(6)

v(x,t)=v(x,t)+Gσ*∇∏，

(7)

微分同胚映射更新公式如下：

φ(x,t+Δt)←φ(x,t)+Δtv(φ(x,t),t)，

(8)

式中:Gσ是一种特定的高斯滤波器，可对速度场、变形域进行平滑处理；∏～为相似性度量；φ为微分同胚映射；Δt为离散时间步长。对于Geodesic-SyN配准算法而言，互相关相似度量公式如下：

(9)

式中：β代表局部均值，x代表窗口的中心位置。

ANTs封装了一些配准方法，可以查询的有21种，大大减少了配准的局限性。配准过程有4个返回值，依次为warpedmovout、warpedfixout、fwdtransforms和invtransforms。在本文中，获取的是第一个返回值，并写入到save_path，使得到得配准结果更精确，且配准速度更快。

3.2 基于ANTs配准的多图谱分割算法流程图

由ANTs配准后将多个图谱的分割结果进行融合得到一个高质量的分割结果。本文在完成ANTs配准工作后，采用了4种不同融合算法进行比较分析，即MV算法、GM算法、ML算法以及RF-SSLP算法[16]，可看出在以上4种融合算法中，RF-SSLP算法的精度最高。本文算法流程如下：

图1 算法流程图Fig.1 Algorithm flow chart

Step 1.预处理阶段，包括对图像进行颅骨剔除、提取感兴趣区域、图谱选择，以此减少脑部其他组织对实验的影响且减小图像块的信息，提高效率。

Step 2.分别进行重采样、ANTs、重采样加微分同胚Demons配准、ANTs加微分同胚Demons配准后比较，使得图谱图像的标记图像与待分割图像的灰度值和对比度处于同一水平。

Step 3.用不同融合算法处理每组的10幅图谱图像的海马体分割结果，比较分析不同融合算法得到的结果图，找到一个与金标准最接近、精度最高的分割结果。

4 实验结果与分析

本文实验采用来源于ADNI(Alzheimer’s Disease Neuroimaging Initiative)包含124个T1-MR样本的子库[17]，本文称为图库1，和来源于伦敦帝国理工学院医学脑部研究数据库(http://brain-development.org/)[18]，本文称为图库2，该图库包含20个T1-MR灰度图像和对应的标记图像样本，其中有67个脑部结构被标记。图库1和图库2均为公共的人脑磁共振数据库。本文实验所需的软件工具有Visual Studio 2010集成开发环境、Cmake跨平台编译器、图像分析工具库ITK[19]、ITKSNAP医学图像可视化软件、ANTs、MATLAB等。

本文在配准阶段，依次采用重采样、ANTs、重采样加微分同胚Demons配准、ANTs加微分同胚Demons配准4种方法；在融合阶段，分别采用MV算法、GM算法、ML算法以及RF-SSLP算法。由多次实验结果分析可得出，ANTs加微分同胚Demons配准后，再用RF-SSLP算法融合，得到的分割结果与金标准最接近。因此，本文给出了用4种配准方法得到的分割结果，将该分割结果用RF-SSLP算法进行融合后的实验对比，同时，也给出了在配准阶段运用ANTs加微分同胚Demons配准方法后，在融合阶段分别用MV算法、GM算法、ML算法以及RF-SSLP算法进行实验比较分析的结果，如图2～5所示，第一列至第三列的图分别为海马体切片图的轴状位、矢状位、冠状位，第四列为海马体的三维立体图。

图2为图库1中RF-SSLP融合算法在不同配准方法中右海马体的分割结果。可明显看出，只采用重采样得到的海马体分割结果不太好，其余3种配准方法效果也并不明显。

为能更直观地看出分割效果，图库2采用金标准和本文实验方法得到的分割结果的重叠图，其中，白色区域为专家手工分割结果，红色区域为本文实验结果。

图3为图库2中RF-SSLP融合算法在不同配准方法中海马体的分割结果。从图3(a)可以看出欠分割现象明显，图3(d)分割效果良好。由于传统的多图配准算法是采用“粗精”配准，而重采样环节和ANTs环节都只是代替了配准环节中的“粗”配准，没有进行“精”配准，导致在图库2 中重采样分割的右海马体和ANTs分割的右海马体均出现明显的欠分割现象。在图3(c)和图3(d)中，微分同胚Demons配准为“精”配准环节，分别采用了重采样加微分同胚和ANTs加微分同胚两种混合配准方法，可以看出，图3(d)分割效果更好，即本文算法对于海马体分割的精度更高。

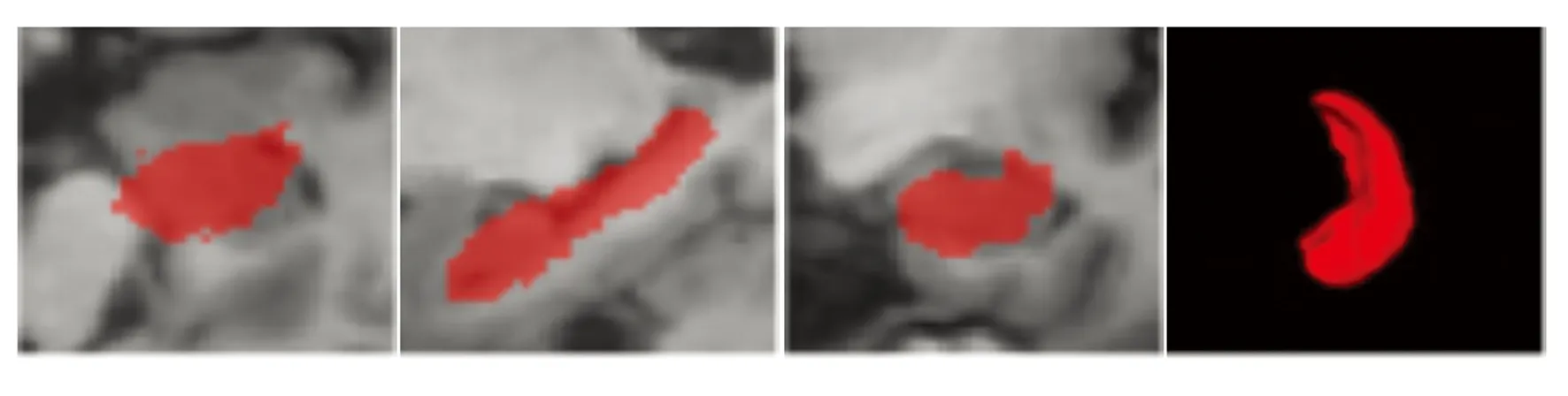
(a) 重采样分割的右海马体(a) Resampling of the segmented right hippocampus

(a) 重采样分割的右海马体(a) Resampling of the segmented right hippocampus

在配准阶段采用ANTs加微分同胚Demons配准后用4种融合算法得到的分割结果如图4所示。

图4为图库1配准阶段采用ANTs加微分同胚Demons配准后各融合算法的分割结果图。可以看出，图4(b)、图4(d)较图4(a)出现了欠分割现象，而图4(c)较图4(a)出现了过分割现象，图4(e)更接近于图4(a),即RF-SSLP融合方法分割精度更高。

(a) 专家手工分割的右海马体(a) Experts manually segment the right hippocampus

(a) 专家手工分割的右海马体(a) Experts manually segment the right hippocampus

同样，在图库2中采用了专家手工分割海马体与分割结果的比较图。

图5为图库2配准阶段采用ANTs加微分同胚Demons配准后各融合算法与金标准的比较图。可直观看出，图5(d)中白色和红色区域重合部分较少，出现了欠分割现象，图5(b)也有小部分欠分割，而图5(c) 白色和红色区域重合部分较多，出现了过分割现象，只有图5(e)中白色和红色区域几乎完全重合，分割结果较好。

本文最后对各融合算法和专家手工分割的重叠率进行比较，比较方法采用Dice相似性测度[20]，Dice取值在0和1之间，Dice值越接近于1，则表示分割结果越精确。本文用相似性测度对实验结果实现定量分析，结果如表1、表2所示。

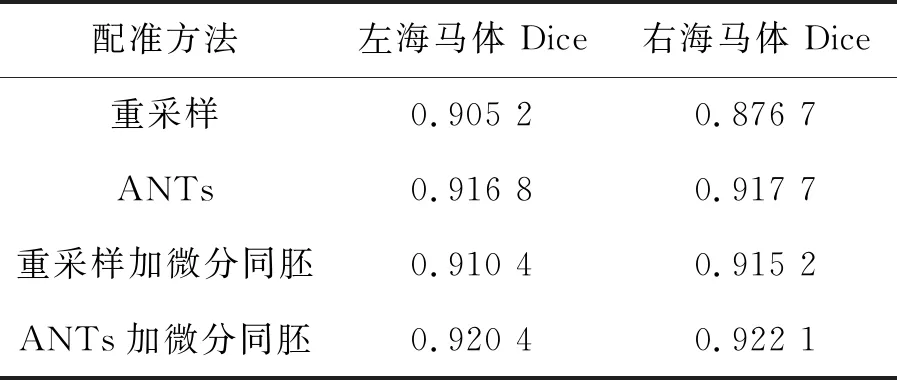
表1 不同配准方法得到的RF-SSLP算法分割结果与金标准的Dice值(图库1) Tab.1 Dice values of gold standard and RF-SSLP algorithm segmentation results obtained by different registration methods (database 1)

表1和表2分别显示了图库1和图库2中用4种配准方法得到的RF-SSLP算法分割人脑MR图像左、右海马体结构与金标准的相似性测度Dice值。由表可知，配准阶段只采用重采样，分割精度较低，采用ANTs加微分同胚Demons配准，分割精度最好。

表2 不同配准方法得到的RF-SSLP算法分割结果与金标准的Dice值(图库2)Tab.2 Dice values of gold standard and RF-SSLP algorithm segmentation results obtained by different registration methods (database 2)

表3和表4分别显示了用ANTs加微分同胚Demons配准在图库1和图库2中MV、GM、ML以及RF-SSLP四种融合算法分割人脑MR图像左、右海马体结构与金标准的相似性测度Dice值。由表可知，利用本文算法对图库1进行海马体分割的实验，RF-SSLP融合算法精度相较于MV、GM、ML融合算法提高了约0.3，0.06，0.05，本文算法对图库2进行海马体分割的实验，RF-SSLP融合算法精度相较于MV、GM、ML融合算法提高了约0.36，0.04，0.04。本文算法分割结果与金标准相似度最高，分割结果最好。

表3 ANTs加微分同胚Demons配准后各融合方法分割结果与金标准Dice值(图库1)Tab.3 Segmentation results of fusion methods and gold standard Dice values after registration of ANTs plus differential homomorphic Demons (database 1)

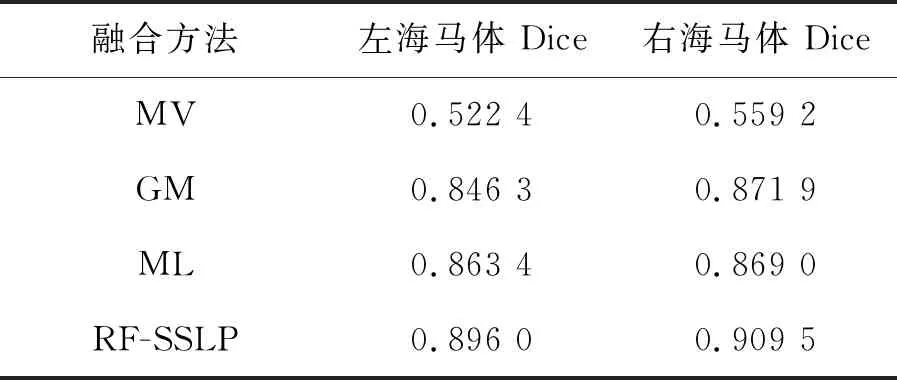
表4 ANTs加微分同胚Demons配准后各融合方法分割结果与金标准Dice值(图库2)Tab.4 Segmentation results of fusion methods and gold standard(database 2)

由于上述图表只是一组数据的实验结果，不足以说明算法的稳定性，因此将所有实验结果绘制成盒装图。

图6和图7分别显示了图库1和图库2中个配准方法的盒装图，从盒装图可以看出，本文分割算法在图库1中分割精度最高，在图库2中右海马体分割精度最高，左海马体分割精度差一些，但是总体比较，可直观看出本文基于ANTs配准的多图谱分割算法相较于其他方法有一定的提高。

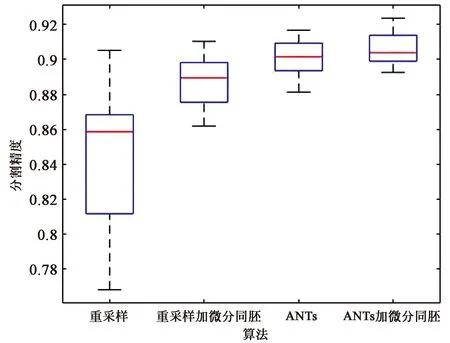
(a)左海马体的盒状图(a) Box plot of left hippocampal

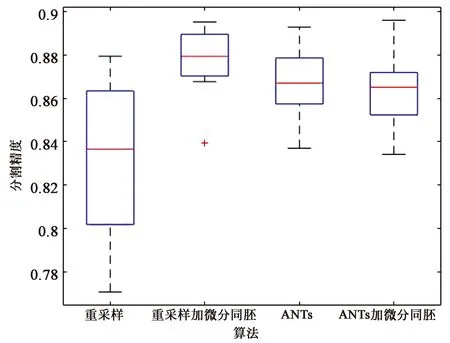
(a)左海马体的盒状图(a) Box plot of left hippocampal

5 结 论

本文在图谱选择阶段，利用提取ROI后的图谱块进行图谱筛选，将筛选出的图谱作为浮动图像进行后续的配准与分割。在多图谱分割算法中，用ANTs代替重采样，并且比较了不同配准方法在RF-SSLP算法中的Dice值；同时，也比较了MV、GM、ML和RF-SSLP的分割结果。实验结果表明，在配准阶段，运用ANTs加微分同胚Demons配准可以使多图谱MR海马体分割算法更精准；在融合阶段，运用RF-SSLP算法可以达到更高的分割精度；在配准阶段和融合阶段，二者结合，得到的结果更接近于金标准；在配准阶段运用ANTs加微分同胚Demons配准后，RF-SSLP算法精度相较于MV、GM和ML提高了3%～5%。