大跨度钢桁悬索桥颤振气动优化措施试验研究

董国朝，许育升，韩艳，李凯，彭元诚

大跨度钢桁悬索桥颤振气动优化措施试验研究

董国朝1，许育升1，韩艳1，李凯1，彭元诚2

(1. 长沙理工大学 桥梁工程安全控制教育部重点实验室，湖南 长沙 410114；2. 中交第二公路勘察设计研究院有限公司，湖北 武汉 430056)

对某大跨度钢桁悬索桥进行颤振试验研究，讨论采取设置中央稳定板、增设抑流板、封闭外护栏部分高度、调整下检修道人行板厚度以及变动水槽等不同气动措施及其相互组合下加劲梁的颤振稳定性能，综合考虑各方面因素得到气动优化方案。研究结果表明：单独采取设置下中央稳定板以及增设抑流板的措施对加劲梁的气动优化效果均不明显。在含有降低下检修道人行板厚度的组合措施中，保留水槽有利于改善加劲梁的颤振稳定性；在不含降低下检修道人行板厚度的组合措施中，移除水槽有利于改善加劲梁的颤振稳定性。外护栏的封闭高度越大，越有利于改善加劲梁的颤振稳定性，且封闭外护栏上部比封闭其下部的影响效果更明显。

大跨度钢桁悬索桥；颤振稳定性；节段模型；气动优化

钢桁梁因具有透风性好、抗扭转刚度大、便于在不具备水路运输的地区施工等优点，常作为大跨度悬索桥加劲梁的断面形式。大跨度悬索桥结构纤柔，阻尼小，加劲梁振动频率低，易发生风致振动。颤振是一种由负阻尼驱动的、空气流动与桥梁结构耦合作用的风致振动现象，对结构具有极强的毁坏性[1]。因此，避免其发生是抗风设计过程中必须严格控制的一个指标。目前，钢桁加劲梁等复杂加劲梁断面的颤振流场机制尚不明确，主要以风洞试验来检验并改善加劲梁断面的颤振稳定性。采用气动措施能从根源上有效提高加劲梁的颤振稳定性，以更小的成本和代价显著优化加劲梁断面，如：增设中央稳定板、加导流板、加装风嘴、中央封槽、封闭护栏以及调整检修道等。近年来，国内外学者通过风洞试验和数值模拟探索了各类气动控制措施对钢桁悬索桥加劲梁颤振稳定性的作用效果[2−7]。欧阳克俭等[8]通过对比PIV风洞试验和CFD数值模拟发现中央稳定板能在桁架梁上下表面的中游附近产生旋涡对，增强了升力的作用，削弱了振动过程中扭转的参与效应。陈政清等[9]发现中央稳定板降低桁架断面的气动负阻尼进而提高了颤振临界风速，并通过能量法证明其作用机理。WANG等[10−11]通过矮寨大桥节段模型风洞试验发现下中央稳定板有利于提高加劲梁颤振稳定性，且长度存在一个最优值。王云飞等[12]发现封闭检修道、中央槽和设置合理高度的下中央稳定板能较明显地改善加劲梁的颤振稳定性。TANG等[13]发现钢桁梁断面在小风攻角时设置下中央稳定板后，下游的上下桥面形成了一对相反的负压区，产生了负能量，降低了颤振频率并提高了颤振临界风速。李明等[14]由风洞试验结果提出封闭中央开槽同时设置上中央稳定板时，增设下稳定板能明显改善钢桁梁的颤振稳定性。虽然目前有很多学者对钢桁悬索桥的颤振稳定性单一气动措施及其组合措施进行了大量的探索，但由于流场机制的复杂性和每座桥梁断面的独特性使得各种气动措施的定量效果是不明确的，甚至定性效果也不是绝对的。因此研究桥梁的气动措施对日后同类桥梁风致振动控制措施的选取具有重要参考意义。以某大跨度钢桁悬索桥为工程背景，首先使用ANSYS软件建立有限元模型获得加劲梁竖弯与扭转振动基频及对应模态质量，并基于节段模型颤振试验研究设置中央稳定板、增设抑流板、封闭护栏、变动水槽和调整下检修道人行板厚度等单一措施及其组合措施对加劲梁颤振稳定性的优化效果，研究结果可为同类桥梁加劲梁的颤振性能研究及气动优化措施选取提供参考。

1 有限元建模

1.1 工程概况

图1(a)为悬索桥的加劲梁原设计断面图，主桁高7.5 m，小节间长7.5 m，左右主桁的中心间距28 m。桥面防撞护栏高1.7 m，上、下检修道护栏高1.5 m，下检修道断面图如图1(b)所示。大桥主缆矢跨比为1:10，主跨为1 200+425 m，吊索纵向标准间距15 m，主缆跨中共设置5对中央扣来形成缆梁固结，如图1(c)所示。大跨钢桁悬索桥采用钢筋混凝土门型桥塔，北侧的塔高191 m，南侧的塔高238 m，塔柱、塔墩均使用矩形空心截面。

大桥跨越峡谷河流，桥址位于地形起伏较大的丘陵地区，其地表类别为D类，计算峡谷的基准高度为215 m，桥面基准风速为25.9 m/s。按现有规范[15]可算得设计基准风速为37.4 m/s，进一步计算得到此大跨钢桁悬索桥成桥时加劲梁的颤振检验风速值大小为：

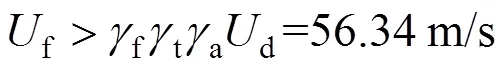
式中：f为颤振稳定性分项系数，此处采用风洞试验方法故取值为1.15；t为风速脉动空间分项系数，取值为1.31；a为攻角效应分项系数，与试验风攻角的范围有关，此处偏保守取值为1。

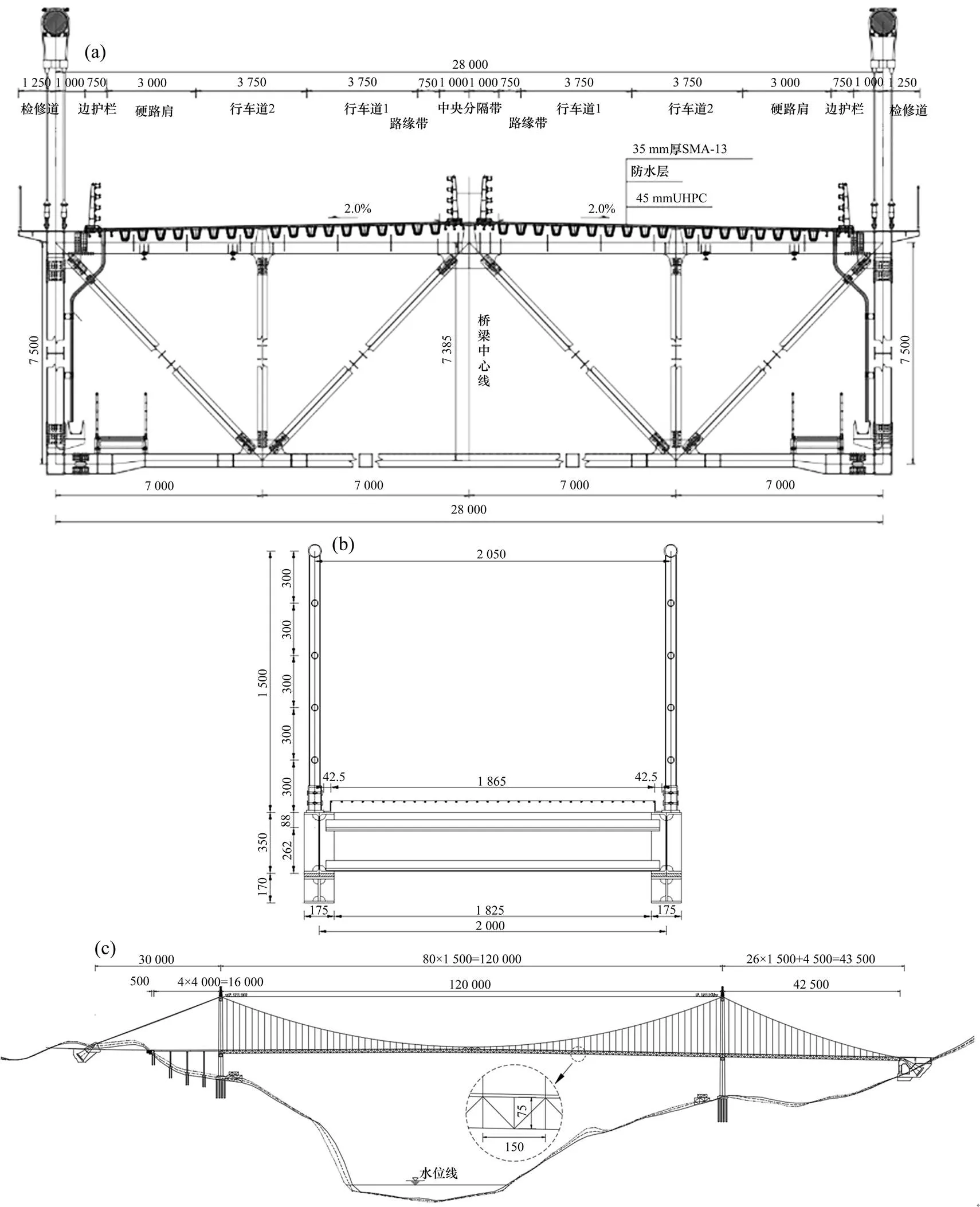
单位：mm

(a) 加劲梁断面图；(b) 下检修道断面图；(c) 桥梁总体布置图

图1 工程背景桥型图

Fig. 1 Bridge pattern of engineering background

1.2 结构动力特性分析

基于有限元软件ANSYS分析桥梁的结构动力特性[16]，建模时以BEAM188模拟钢桁加劲梁，以LINK10模拟主缆及吊杆，以BEAM4模拟桥塔，桥面系正交异性板和UHPC用SHELL181模拟，忽略桥面的横坡。采用等效密度计算方法来准确模拟质量分布，桥梁有限元模型如图2所示，桥梁的自振特性如表1所示。该桥选择一阶正对称竖弯、扭转的频率进行试验，对应振型如图3所示。

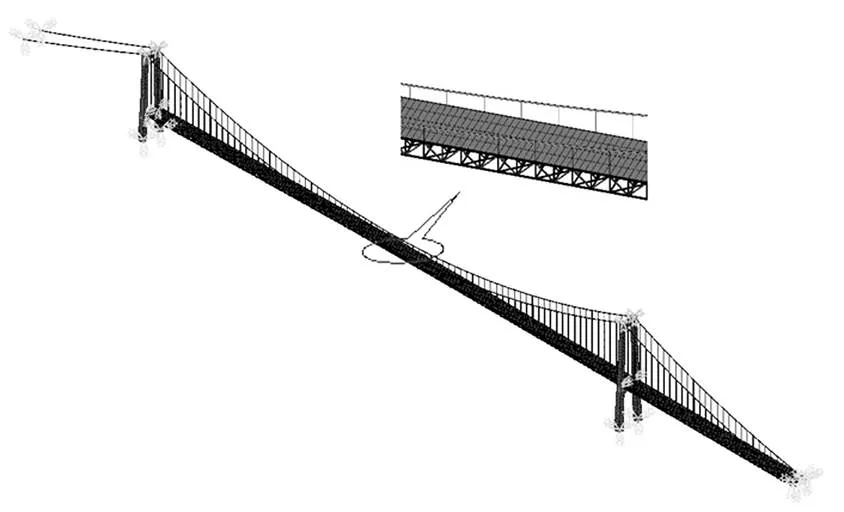
图2 桥梁有限元模型

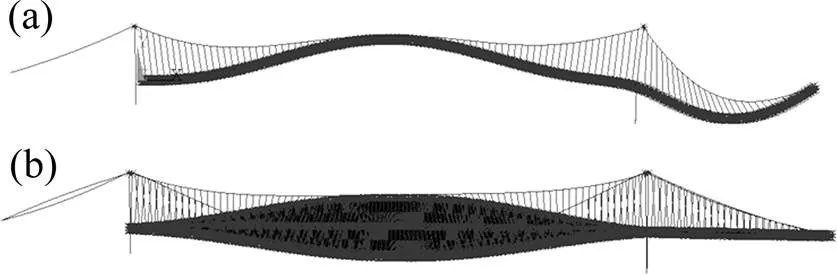
(a) 一阶正对称竖弯；(b) 一阶正对称扭转

表1 桥梁自振特性

2 节段模型颤振试验

颤振试验在长沙理工大学风工程与风环境研究中心边界层风洞进行，风洞的试验段截面尺寸为4.0 m×3.0 m×21.0 m。试验风速比为4.02，严格按缩尺比模拟实桥各参数值，试验参数如表2所示。原设计加劲梁断面在=±5°，±3°，0°攻角下进行颤振稳定性试验，模型布置如图4所示。

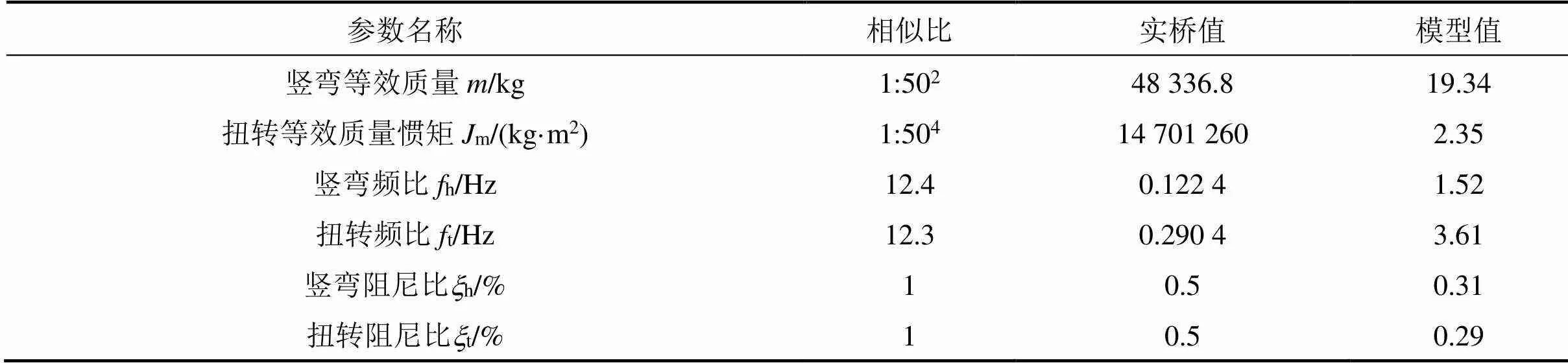
表2 节段模型试验的模型主要参数

图4 风洞试验中的节段模型

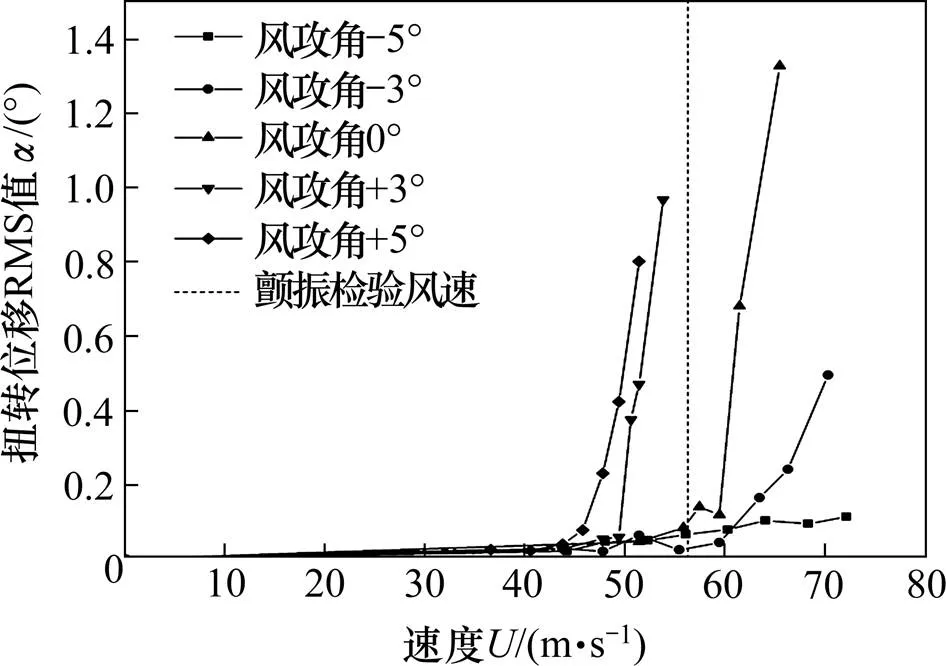
图5 原设计试验扭转位移响应结果

原设计加劲梁实桥的颤振检验结果如图5及表3所示。图5结果显示：0°和−3°攻角对应曲线的颤振扭转发散点在靠近竖线的右边，表明出现扭转位移发散的风速值大于颤振检验风速值。而表3结果表明：0°攻角时原设计钢桁加劲梁实桥的颤振临界风速值相比56.34 m/s仅高出5.6%，安全余量不足。−5°攻角虽有较大的富余，但+3°、+5°攻角加劲梁试验结果值都明显低于颤振检验风速理论计算值，且+5°攻角为最不利攻角。

表3 各攻角原设计加劲梁断面颤振试验结果

3 气动优化措施研究

若定义进行气动优化后该桥加劲梁的颤振临界风速增加率为，则按照式（2）计算：

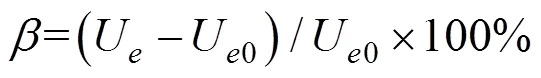
采用9种不同类型的气动优化措施进行了试验。上中央稳定板的高度不宜高出内侧护栏高度，此大桥内侧护栏高为1.7 m。通过初步试验发现上中央稳定板高度取1.5 m的试验结果最优，继续增加其高度并不能有效提升颤振临界风速值，反而会增加其加劲梁的阻力且同时影响视觉效果。综合考虑施工可行性和钢桁架高度，采用0.5 m和1 m高的下中央稳定板进行试验。另外，合理调整加劲梁的附属设施也可以优化其气动性能。基于此，本文对最不利攻角(+5°)下的加劲梁原设计断面进行气动优化研究，试验的具体气动措施内容如表4所示，具体实施位置如图6所示。

3.1 单一气动措施研究

首先，对该悬索桥原设计加劲梁断面采用单一气动措施①，②，④，⑤和⑥进行节段模型颤振试验，试验结果如表5所示。

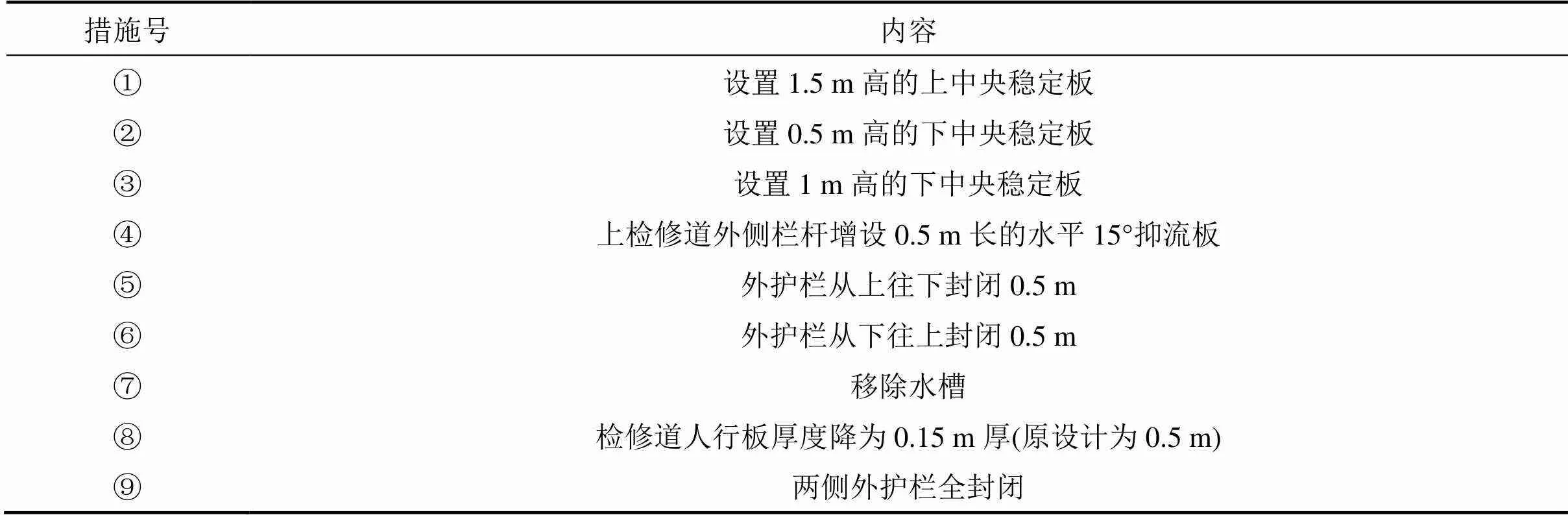
表4 气动措施内容

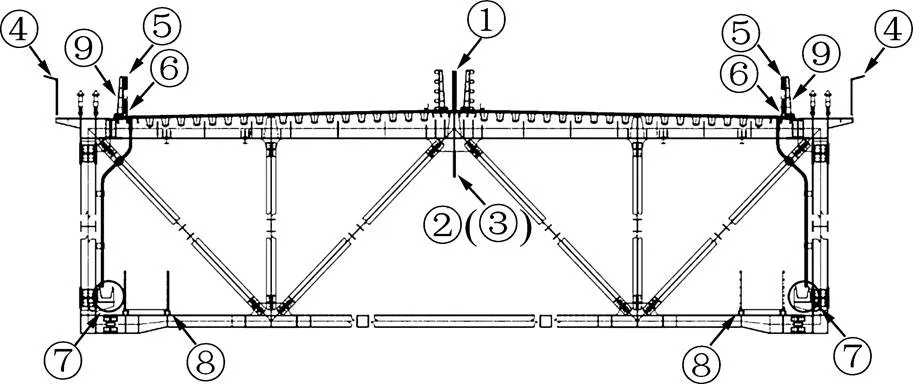
图6 气动措施实施位置示意图

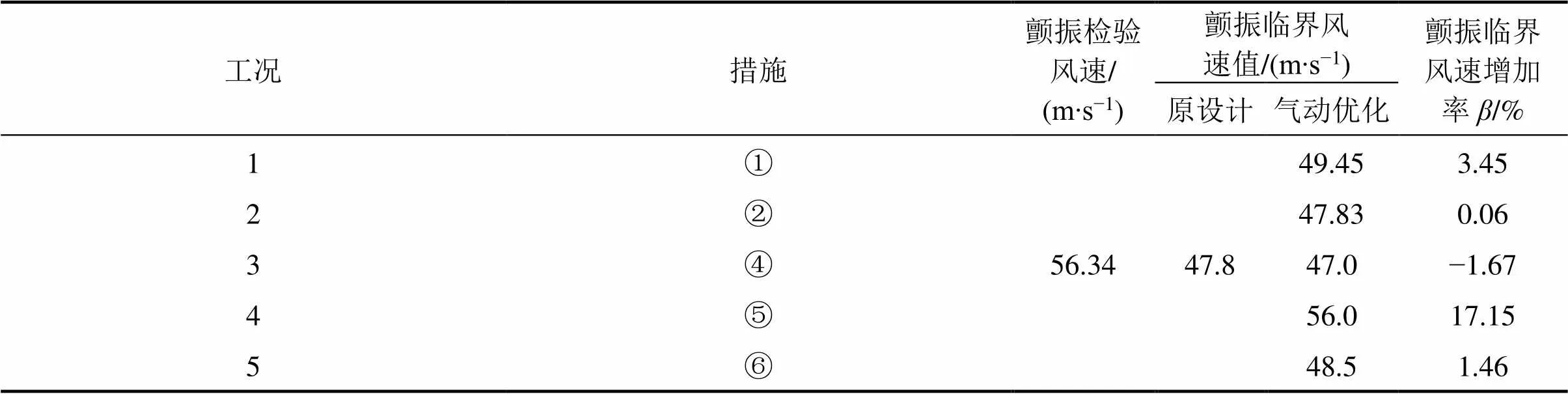
表5 单一气动措施节段模型颤振试验结果

由试验结果可见，加劲梁上增设0.5 m长的水平15°抑流板(措施④)颤振临界风速值相比原设计断面试验值略有降低，不利于优化该桥加劲梁断面的气动稳定性能。单独设置1.5 m高的上中央稳定板(措施①)、0.5 m长的下中央稳定板(措施②)和从下往上封闭护栏0.5 m(措施⑥)均起到小幅度抑制加劲梁断面颤振的作用但其增加率均低于5%。措施①，②，⑥的作用效果虽不明显，但可以加入组合措施进一步研究。从上往下封闭护栏0.5 m(措施⑤)对应的加劲梁颤振临界风速值比原设计提高17.15%，对加劲梁气动优化效果虽显著，但还是略小于该钢桁悬索桥加劲梁理论计算的颤振检验风速值。同时，从上往下封闭护栏0.5 m(措施⑤)相比于从下往上封闭护栏0.5 m(措施⑥)更有利于优化加劲梁的颤振性能，故在后续组合措施中进一步研究护栏的封闭情况对加劲梁颤振稳定性的改善效果。以上措施单独采用时均不能满足颤振稳定性要求，故需采取多种气动措施相互组合进行研究，进一步优化加劲梁颤振稳定性能。

3.2 组合气动措施研究

当采用单一气动措施不能满足要求时，合理地组合不同气动措施能够进一步改善加劲梁的颤振稳定性。因此，有必要进一步探索各气动措施的组合使用对改善加劲梁颤振稳定性的综合影响。在单一气动措施的试验结果中，设置上、下中央稳定板以及封闭护栏的措施在一定程度上增大了该悬索桥加劲梁的颤振临界风速值，故将进一步研究其在组合措施中的综合影响。另外，在组合措施中加入移除水槽(措施⑦)和将下检修道人行板高度降为0.15 m厚(措施⑧)的下部气动优化措施，试验结果如表6所示。

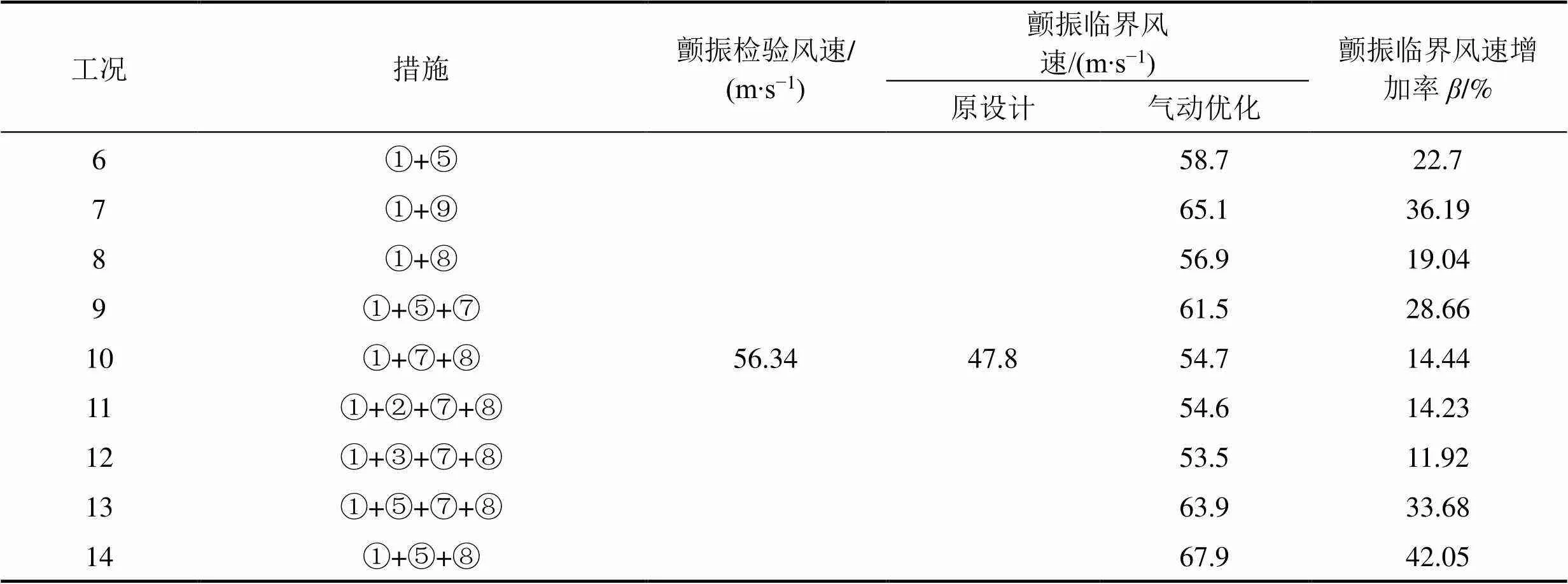
表6 组合气动措施节段模型颤振试验结果

相比于单一气动措施，试验使用组合措施所得的临界风速值均明显增大。由表6结果可知，工况7相比于工况6，颤振临界风速值增大了10.9%，较大地提升了加劲梁的颤振临界风速值。再结合工况4和工况5，可以发现护栏封闭高度越大，颤振临界风速增加率越大，越有利于改善加劲梁的颤振稳定性能，且封闭护栏上方相对于封闭护栏下方更能明显地改善加劲梁气动稳定性。对比工况6、7和8可得，联合使用1.5 m高的上中央稳定板和全部封闭两侧外护栏(工况7)加劲梁的颤振临界风速增加率达到了36.19%，气动优化效果最显著。但全封闭护栏不仅会影响景观效果、消耗更多材料，还会导致加劲梁阻力系数增大，进而导致静风位移过大，故该桥不建议采取全封闭护栏这一气动措施。

由工况10，11和12分析得，在联合使用上中央稳定板、移除水槽和下检修道人行板厚度降为0.15 m厚的组合措施中，设置0.5 m长的下中央稳定板(工况11)相比于没有设置下中央稳定板(工况10)的颤振临界风速值略有降低，但其气动优化效果相比设有1 m长的下中央稳定板(工况12)更优。进一步分析可得，该桥设置下中央稳定板在组合措施中呈现不利趋势，且高度越大越不利。工况8，13和14分别是基于工况1，9和13增加了下检修道人行板厚度降低为0.15 m厚(措施⑧)这一下部气动措施进行加劲梁的颤振试验。试验结果表明，组合措施中使用下检修道人行板厚度降低为0.15 m厚的措施可提高加劲梁的颤振临界风速值，改善加劲梁的气动稳定性。但是，调整下部附属结构对加劲梁气动稳定性改善效果不如采用上部气动措施明显。由于桁架梁桥面处的风环境相对简单，在桥面采取气动措施易起到阻止桥面涡旋增大的作用，而下部的桁架杆件较多，风环境相对复杂，作用效果也相对不明显。

在设置1.5 m高的上中央稳定板和从上往下封闭护栏0.5 m的联合措施中，移除水槽(工况9)相比保留水槽(工况6)，颤振临界风速值增大了4.77%。在设置1.5 m高的上中央稳定板和将下检修道人行板厚度降低为0.15 m厚的联合措施中，移除水槽(工况10)相比保留水槽(工况8)，颤振临界风速值降低了3.87%。进一步对比工况13和工况14，移除水槽(工况13)相比保留水槽(工况14)，颤振临界风速值降低了5.89%。可以看出，在组合措施中使用下检修道人行板厚度降为0.15 m厚的气动措施时，保留水槽更有利于提高颤振临界风速；在组合措施中不使用下检修道人行板厚度降为0.15 m的气动措施时，移除水槽更有利于提高颤振临界风速。即在组合措施中单独采用移除水槽和将下检修道人行板厚度降为0.15 m厚的气动措施有利于提高加劲梁的颤振临界风速值，但同时使用时反而对结果不利。

综上所述，工况10，11和12的气动优化效果均明显优于原设计，但仍未能达到颤振稳定性要求；工况6，8和9的试验结果值虽均超出了钢桁悬索桥加劲梁理论计算的颤振检验风速值，但安全余量都比较小。工况7，13和14均能达到颤振稳定性要求且安全余量较充裕，但工况7和工况13相比于工况14，颤振临界风速值略低且改动了原设计方案，综合考虑下，采取组合措施14作为气动优化的最终方案。

3.3 优化方案的加劲梁颤振性能验证

节段模型的气动优化试验是基于最不利攻角(+5°)进行的，以工况14即设置1.5 m高的上中央稳定板(措施①)、从上往下封闭外护栏0.5 m(措施⑤)和将检修道人行板厚度降为0.15 m厚(措施⑧)作为最优气动措施进行各攻角的颤振试验。

采取气动措施的加劲梁节段模型在±5°，±3°和0°各攻角下的颤振试验结果如表7所示。采取最优方案进行气动优化后，各攻角下加劲梁的颤振稳定性能均能满足要求且具有充裕的安全余量。

表7 采取气动措的加劲梁各攻角颤振试验结果

4 结论

1) 在加劲梁外护栏处增设0.5 m长的15°抑流板略降低了加劲梁的颤振稳定性，单独设置或在组合措施中加入下中央稳定板对加劲梁的气动优化作用效果较低。相比于单一气动措施，合理采取多种气动措施组合，能进一步提高加劲梁的颤振临界风速，改善加劲梁的气动稳定性。

2) 在组合措施中单独采用移除水槽和将下检修道人行板厚度降为0.15 m厚均能进一步增大颤振临界风速值，但同时使用时反而会减小其值。

3) 组合措施中使用调整下检修道人行板厚度的气动措施能进一步改善加劲梁的颤振稳定性。在桁架梁下部结构使用气动措施对改善加劲梁颤振稳定性有一定的影响，但不如在其上部使用气动措施的作用效果更明显。

4) 外护栏封闭高度越大，对加劲梁的气动优化作用越显著，但全封闭时景观效果较差。从上往下封闭外护栏一定长度相比于从下往上封闭相同长度外护栏的气动优化结果更能改善加劲梁的颤振稳定性。

[1] 陈政清. 桥梁风工程[M]. 北京: 人民交通出版社, 2005. CHEN Zhengqing. Bridge wind engineering[M]. Beijing: China Communications Press, 2005.

[2] TANG Haojun, LI Yongle, Shum K M, et al. Non- uniform wind characteristics in mountainous areas and effects on flutter performance of a long-span suspension bridge[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2020, 201: 104177.

[3] 李永乐, 武兵, 汪斌, 等. 扭心偏移对桁梁桥颤振临界风速影响的试验研究[J]. 振动与冲击, 2018, 37(21): 165−170. LI Yongle, WU Bing, WANG Bin, et al. Tests for effects of torsional center offset on flutter critical wind velocity of a truss bridge[J]. Journal of Vibration and Shock, 2018, 37(21): 165−170.

[4] HUA Xugang, WANG Chaoqun, LI Shengli, et al. Experimental investigation of wind-induced vibrations of main cables for suspension bridges in construction phases[J]. Journal of Fluids and Structures, 2020, 93: 102846.

[5] 伍波, 王骑, 廖海黎. 双层桥面桁架梁软颤振特性风洞试验研究[J]. 振动与冲击, 2020, 39(1): 191−198. WU Bo, WANG Qi, LIAO Haili. Wind tunnel tests for soft flutter characteristics of double-deck truss girder[J]. Journal of Vibration and Shock, 2020, 39(1): 191−198.

[6] 徐昕宇, 李永乐, 廖海黎, 等. 双层桥面桁架梁三塔悬索桥颤振性能优化风洞试验[J]. 工程力学, 2017, 34(5): 142−147. XU Xinyu, LI Yongle, LIAO Haili, et al. Flutter optimization of a double-deck truss-stiffened girder three-tower suspension bridge by wind tunnel tests[J]. Engineering Mechanics, 2017, 34(5): 142−147.

[7] LI Yongle, TANG Haojun, WU Bing, et al. Flutter performance optimization of steel truss girder with double-decks by wind tunnel tests[J]. Advances in Structural Engineering, 2018, 21(6): 906−917.

[8] 欧阳克俭, 陈政清. 中央稳定板提高颤振稳定性能的细观作用机理[J]. 振动与冲击, 2016, 35(1): 11−16. OUYANG Kejian, CHEN Zhengqing. Micro-mechanism of a central stabilizer for improving a bridge’s flutter stability[J]. Journal of Vibration and Shock, 2016, 35(1): 11−16.

[9] 陈政清, 欧阳克俭, 牛华伟, 等. 中央稳定板提高桁架梁悬索桥颤振稳定性的气动机理[J]. 中国公路学报, 2009, 22(6): 53−59. CHEN Zhengqing, OUYANG Kejian, NIU Huawei, et al. Aerodynamic mechanism of improvement of flutter stability of truss-girder suspension bridge using central stabilizer[J]. China Journal of Highway and Transport, 2009, 22(6): 53−59.

[10] WANG Kai, LIAO Haili, LI Mingshui. Flutter suppression of long-span suspension bridge with truss girder[J]. Wind and Structures, 2016, 23(5): 405−420.

[11] 李春光, 张志田, 陈政清, 等. 桁架加劲梁悬索桥气动稳定措施试验研究[J]. 振动与冲击, 2008, 27(9): 40− 43, 181. LI Chunguang, ZHANG Zhitian, CHEN Zhengqing, et al. Experimential study on the aerodynamic stability measure of a suspension bridge with truss stiffening girder[J]. Journal of Vibration and Shock, 2008, 27(9): 40−43, 181.

[12] 王云飞, 汪斌, 李永乐, 等. 大风攻角下钢桁梁悬索桥颤振性能研究[J]. 应用基础与工程科学学报, 2019, 27(2): 384−390. WANG Yunfei, WANG Bin, LI Yongle, et al. Flutter performance study of steel truss girder suspension bridge under large angles of attack[J]. Journal of Basic Science and Engineering, 2019, 27(2): 384−390.

[13] TANG Haojun, LI Yongle, WANG Yunfei, et al. Aerodynamic optimization for flutter performance of steel truss stiffening girder at large angles of attack[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2017, 168: 260−270.

[14] 李明, 孙延国, 李明水. 大跨度钢桁梁悬索桥颤振稳定措施试验研究[J]. 振动与冲击, 2018, 37(13): 182−189. LI Ming, SUN Yanguo, LI Mingshui. Tests for flutter stability measures of a long-span suspension bridge with steel truss girders[J]. Journal of Vibration and Shock, 2018, 37(13): 182−189.

[15] JTG/T 3360−01−2018, 公路桥梁抗风设计规范[S]. JTG/T 3360−01−2018, Wind-resistant design specification for highway bridges[S].

[16] 祝志文, 王艺静, 吴其. 大跨度悬索桥主缆空缆状态振动模态分析[J]. 铁道科学与工程学报, 2018, 15(11): 2833−2841. ZHU Zhiwen, WANG Yijing, WU Qi. Modal analyses of large-span suspension bridges at free main cable stage[J]. Journal of Railway Science and Engineering, 2018, 15(11): 2833−2841.

Experimental research on flutter aerodynamic optimization measures of long-span steel truss suspension bridge

DONG Guochao1, XU Yusheng1,HAN Yan1, LI Kai1, PENG Yuancheng2

(1. School of Civil Engineering, Key Laboratory for Safety Control of Bridge Engineering, Ministry of Education and Hunan Province, Changsha 410114, China; 2. CCCC Second Highway Consultants Co., Ltd., Wuhan 430056, China)

An experimental investigation on a long-span steel truss suspension bridge was carried out in this paper. Based on the wind tunnel test results, the effects of different aerodynamic measures, such as setting up the central stabilizing plates, adding the flow suppression plate, sealing partial outer guardrail, adjusting the thickness of pedestrian slab of lower access road, and their combinations on the flutter stability of the main girder were discussed. The aerodynamic optimization scheme was determined by considering various factors. The results show that the improvement of flutter stability is not significant when only setting the lower central stabilizer plate or adding the flow suppression plate alone. In the combined measures to reduce the thickness of pedestrian slab of lower access road, retaining the water channel is beneficial to improve the flutter stability of the stiffened beam. However, in the combined measures without reducing the thickness of the pedestrian slab of the lower access road, the removal of the flume is beneficial to improve the flutter stability of the stiffened beam. The higher the enclosed height of the outer guardrail is, the more beneficial it is to improve the flutter stability. And it is better to close the upper part of the outer guardrail than to close the lower part.

long-span steel truss suspension bridge; flutter stability; segment model; aerodynamic optimization

10.19713/j.cnki.43−1423/u.T20200533

U447

A

1672 − 7029(2021)04 − 0949 − 08

2020−06−11

国家自然科学基金优秀青年基金资助项目(51822803)；湖南省杰出青年基金资助项目(2018JJ1027)；湖南省教育厅优秀青年基金资助项目(16B011)；湖南省研究生科研创新资助项目(CX20200848)

韩艳(1979−)，女，江苏连云港人，教授，博士，从事大跨度桥梁风致振动与振动控制研究、风−车−桥耦合振动与行车安全性研究；E−mail：ce_hanyan@163.com

(编辑 涂鹏)