荷载作用下短路基处AC+CPC复合式路面结构应力响应分析

郑木莲，刘富强，王涛，王帅

荷载作用下短路基处AC+CPC复合式路面结构应力响应分析

郑木莲1，刘富强1，王涛2，王帅3

(1. 长安大学 特殊地区公路工程教育部重点实验室，陕西 西安 710064；2. 北京交通大学 土木建筑工程学院，北京 100044；3. 中交公路规划设计院有限公司，北京 100032)

为研究短路基处斜向预应力混凝土上覆沥青层(AC+CPC)复合式路面结构在荷载作用下的应力响应，以短路基处AC+CPC复合式路面结构为研究对象，应用ANSYS有限元软件建立AC+CPC复合式路面结构三维有限元模型，分析短路基处AC+CPC复合式路面结构在荷载作用下的应力响应。研究结果表明：两桥(隧)之间路基长度少于200 m均可视为短路 基；CPC层层底的弯拉应力最大，特别是板的纵缝边缘中部和横缝中部位置，分别为1.385 5 MPa和1.359 4 MPa，从而得知短路基处AC+CPC复合式路面结构的临界荷位为板的纵缝边缘中部；采用麦考特法和通用全局优化算法，得到斜向预应力混凝土层层底的拉应力计算公式。

短路基；复合式路面；AC+CPC；应力；有限元

对于修建在丘陵或山岭区的高速公路，很多地段设有桥梁、隧道、涵洞等构造物。在两构造物间容易出现夹一段短路基的情况。由于短路基长度较短，施工场地有限，致使路基和基层等结构层很难充分压实，该位置在车辆荷载作用下路面结构受力比较复杂。周娟兰等[1]对设置应力吸收层的复合式路面在车辆荷载和温度荷载共同作用下反射裂缝的扩展路径进行模拟，研究结果显示设置应力吸收层可有效扩散裂尖应力。张明杰等[2]对复合式路面和半刚性路面力学响应进行了对比分析，研究结果显示复合式路面沥青层内剪应力和水平拉应变的最大值分别较半刚性路面减少13%和21%。ZHOU 等[3]对设置桥头搭板的路桥过度段的力学响应进行了分析。YAO 等[4]对公路弯道处桥头跳车的路面力学计算分析，研究结果显示桥头搭板处容易出现应力过大、集中等现象，需要进行补强设计。重载交通对路面极易造成结构性破坏，对其作用下的应力应变分析也是很多学者研究的方向[5−7]。基于短路基差异沉降量较普通路段大、短路基处路面结构受力比较复杂及设置桥头搭板对缓解差异沉降不显著等不足，将AC+CPC复合式路面应用到短路基处减弱该处的差异沉降。本文对短路基处该种路面结构在荷载作用下的应力响应进行分析。

1 短路基的界定与斜向预应力混凝土

1.1 短路基的界定

国内公路工程中对于短路基尚没有明确的界定，铁道部建技[2003]97号文明确规定：Ⅰ级铁路桥梁较密集地段，两台尾之间路基长度<150 m，且能满足设桥条件时，应以桥代路形式通过[8]。陕西省交通运输厅对≤200 m的路基，一般建议采用贫混凝土基层上加铺沥青层的路面结构。

短路基所处地形地质条件较为复杂，此路段往往会对驾驶员的心理产生一定的影响。图1为心率与车速和道路平面线形之间的关系图。

振动对人体精神、生理均会产生一定的影响，从而影响驾驶员的判断。汽车行驶速度、路面类型和平整度均会对道路行驶舒适度产生一定影响。潘晓东提出通过驾驶员的脉搏数和血压的变动规律，研究道路线形构造对其形成的心理和生理上的负担程度，用实验和数理统计的方法建立驾驶员心理、生理上负担程度的评价指标，评价现有公路的行车安全性和舒适性[9]。图2为测定对象区间和脉搏变动及血压变动特性。研究结果显示驾驶员行驶过程中出现2次振动时间超过10 s以上能够有效缓解其紧张及不适感觉。图1和图2中的测试数据均为多次试验的平均值。目前，对于高速公路而言，车速一般控制在80～120 km/h。然而对于修建在丘陵或山岭区的高速公路，由于地形地貌条件复杂及桥梁、隧道等构造物较多的特点，基于安全考虑，在该文研究中选取短路基等特殊路段的车速为70～80 km/h。短路基两构造物间按照此速度行驶在10 s内所行驶的距离为194～220 m，当两构造物间路基长度超过200 m左右时，对车辆行驶舒适性产生的影响较小。

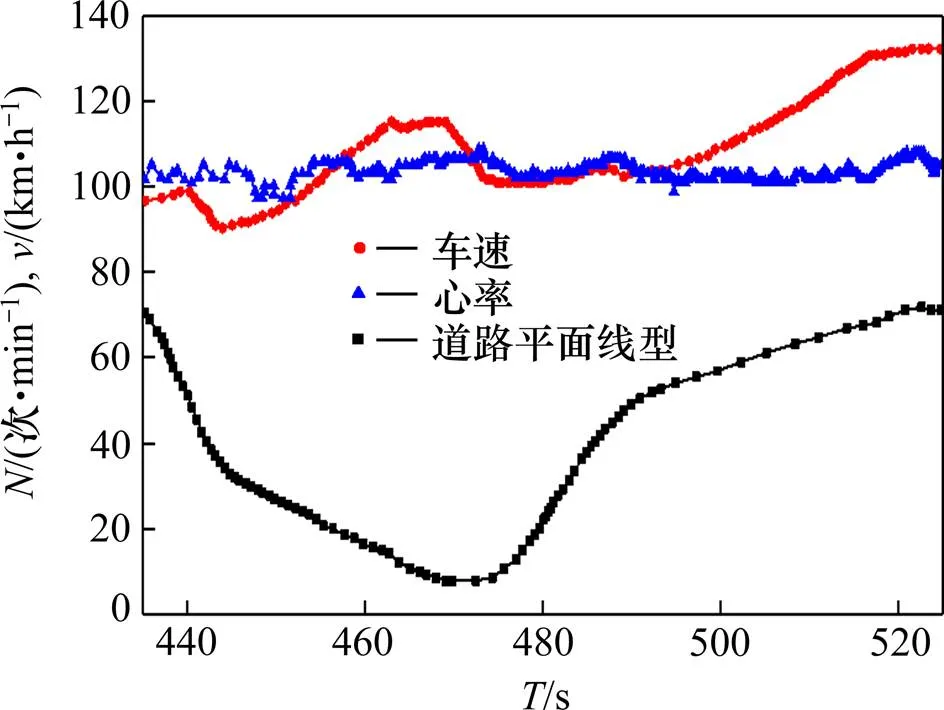
图1 心率与车速和道路平面线形关系

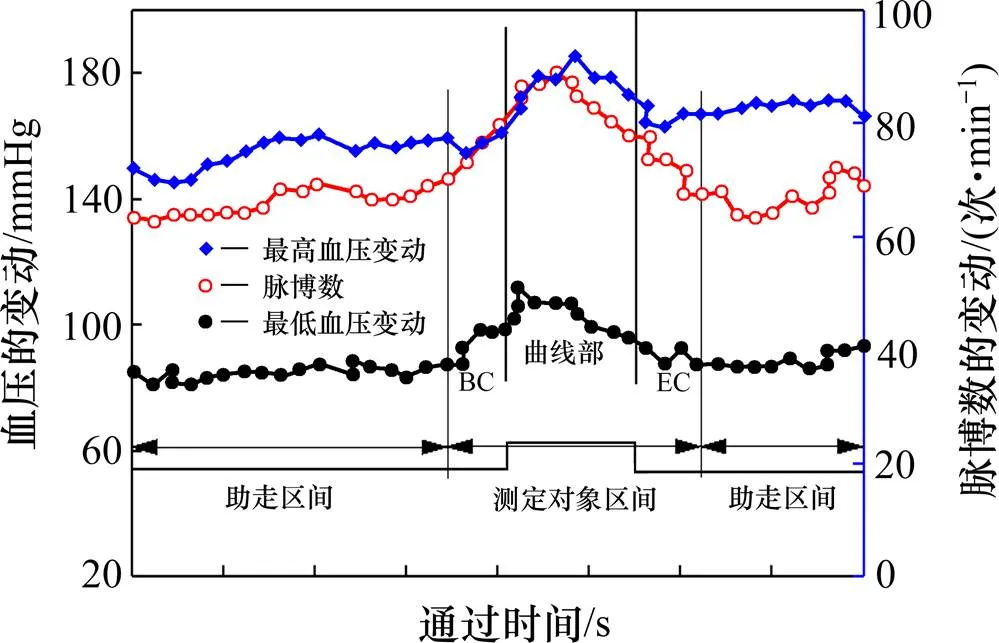
图2 测定对象区间和脉搏变动及血压变动特性

根据研究成果，为了有效降低短路基因差异沉降对运行车辆舒适性造成的不利影响，在两桥(隧)之间短路基处尽可能设置较长的过渡段。结合陕西省交通运输厅以及铁道部建技等相关规定，对于短路基长度适当放宽，认为受到地质、地貌等条件限制，在两桥(隧)之间路基长度少于200 m均可视为短路基。

1.2 斜向预应力混凝土

AC+CPC复合式路面作为一种新型路面结构，在水泥混凝土内部设置双层斜向预应力筋，使预应力筋与路面纵向成一定角度，在路面横向和纵向都产生预应力，实现在很大长度不设置接缝，能够解决因接缝产生损害使普通混凝土路面破损的问题，有效提高水泥混凝土路面使用性能和寿命[10]。CPC路面示意图如图3所示。

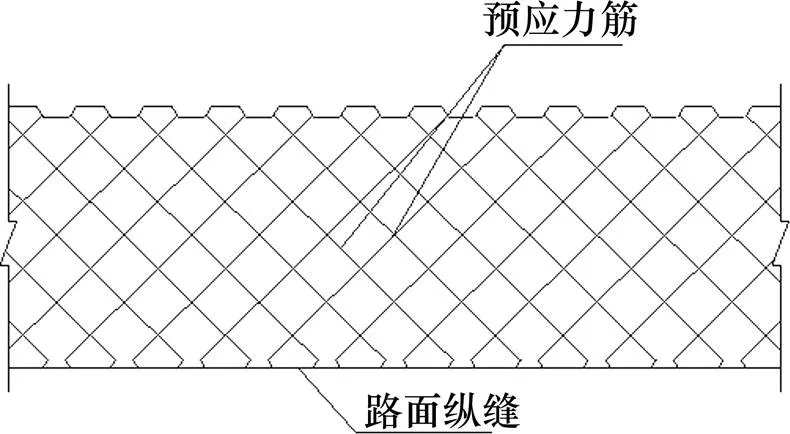
图3 CPC路面示意图

2 短路基处AC+CPC复合式路面结构计算理论与模型

2.1 计算理论

短路基处AC+CPC复合式路面结构如图4所示。除此之外还包括路肩、路面排水系统、斜向预应力混凝土路面板的端部处理和接缝设计、斜向预应力混凝土板的配筋等组成部分。AC+CPC复合式路面可采用弹性半空间地基上的斜向预应力混凝土弹性薄板上覆弹性沥青层的结构体系。

2.2 计算模型

2.2.1 CPC板有限元模型

CPC板、沥青层及基层是规则的矩形板体，采用边界为正交的六面体单元进行分析。在ANSYS有限元建模过程中选取solid45单元。

2.2.2 斜向预应力筋模型

AC+CPC复合式路面结构中布置有双层斜向预应力筋，CPC结构层预应力筋用LINK8单元来模拟，杆单元受力分布均匀。预应力筋的直径为13.2 mm，弹性模量195 000 MPa，极限抗拉强度1 470 MPa。本文在建模分析过程中采用整体式初始应变法进行计算分析。

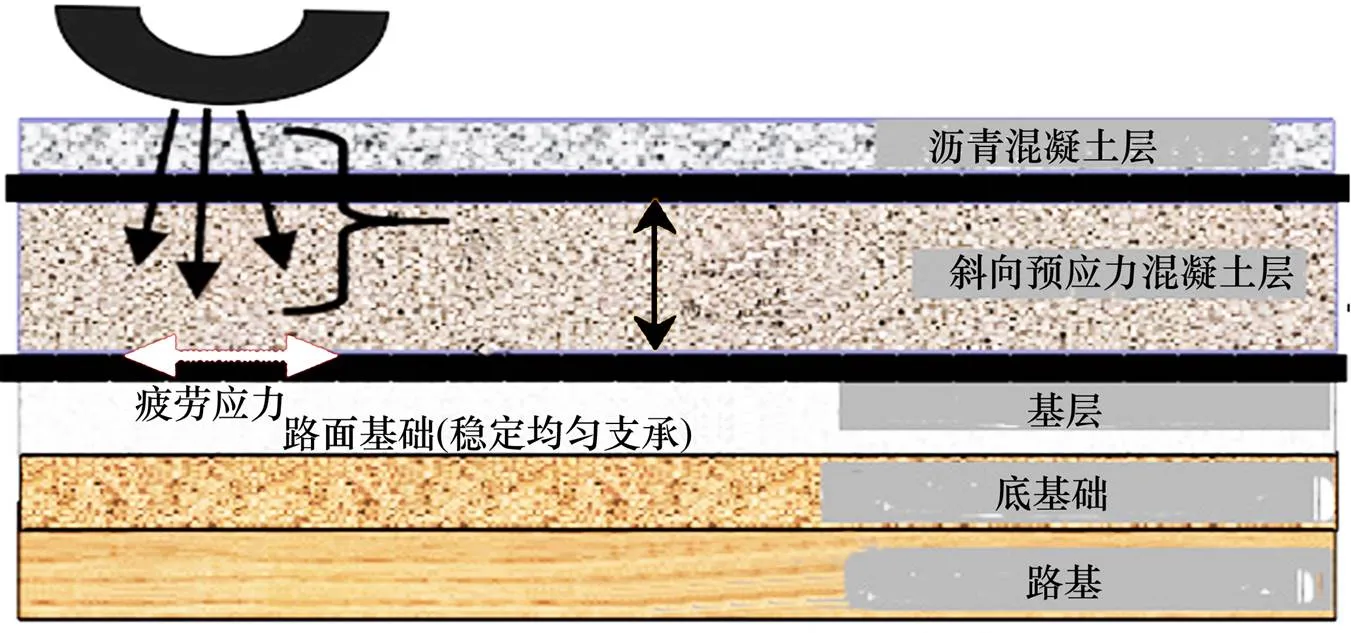
图4 AC+CPC复合式路面结构

2.2.3 CPC层与基层间接触有限元模型

AC+CPC复合式路面结构中设置了滑动层，具有一定的摩擦因数，层间接触条件既不是连续的也不是光滑的，模拟层间接触可以采用接触单元的方式。

建立合适的层间接触模型，可以提高AC+CPC复合式路面结构分析的精确性[11]。ANSYS有限元分析软件可以提供多种接触单元，对于AC+CPC复合式路面结构而言可以采用刚柔面面接触单元，斜向预应力混凝土板当做刚性目标面，采用Targe170来模拟目标面，接触面采用Conta174来模拟[12−13]。目标单元和接触单元形成接触对。把斜向预应力混凝土板底作为目标面，把基层顶面作为接触面，用Targe170和Conta174来模拟，接触面处设置摩擦因数，摩擦因数一般取0.8。

2.2.4 地基有限元模型

在分析刚性路面应力时一般采用弹性地基上薄板模式，对于地基的假定主要有2种类型，一种是弹性半空间地基，另一种是温克勒地基。大量的试验表明，基于弹性地基理论所计算在荷载作用下的应力和实际情况相差不大，所以在进行分析计算时采用弹性层状半空间地基。

3 AC+CPC复合式路面模型建立

3.1 模型的边界条件和荷载加载方式

复合式路面结构的模型边界条件为：1) 在经过收敛性分析之后地基取有限尺寸；2) 对地基底面施加固定约束，各点的自由度为0，地基四周垂直面受到和轴方向的约束；3) 沥青层和基层的四周垂直面为和轴方向约束，基层和地基之间为光滑接触；4) 斜向预应力混凝土板的四周设为完全自由边界；5) 在斜向预应力混凝土板和基层之间设置接触单元，层间摩擦因数取为0.8。

行车荷载采用标准轴载BZZ-100，在建模过程中将模型简化为二维问题，把当量圆荷载简化为线荷载，把双圆均布荷载转化为矩形的均布荷载，矩形的边长为20 cm，接地压强为0.625 MPa，轴载的间距为18 cm。加载面的布置和轮载作用等效转化为矩形图如图5所示。

单位：cm

3.2 计算参数及模型

AC+CPC复合式路面结构计算参数如表1所示，模型如图6所示。

3.3 模型尺寸

在确定模型尺寸时，分别对模型的宽度和长度进行收敛性分析。首先确定长度值为10.8 m，不同宽度取值下CPC层底弯拉应力及路表弯沉如图7所示。

表1 路面结构计算参数

注：预应力筋的直径为13.2 mm，弹性模量195 000 MPa，极限抗拉强度1 470 MPa。

图6 模型图

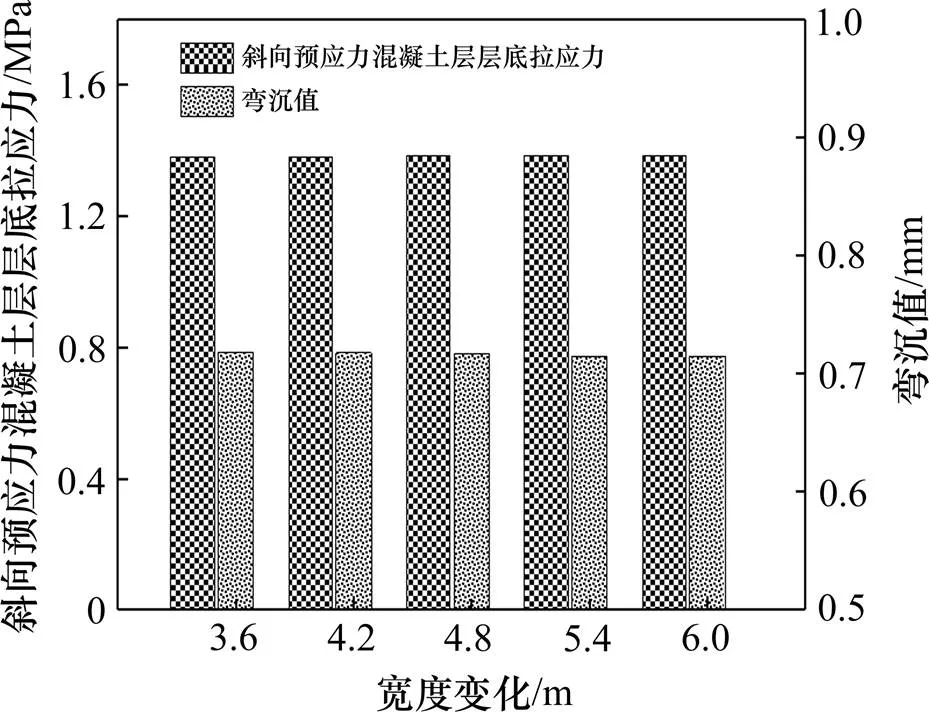
图7 CPC板宽度取值及其计算结果

从计算结果能够看出，当板长一定时，宽度变化对路表弯沉影响不大，宽度在达到5.4 m时层底弯拉应力已经收敛不再变化。鉴于模型划分网格的方便，本模型选取宽度值为5.4 m。不同长度取值下斜向预应力混凝土层底弯拉应力及路表弯沉计算结果如图8所示。从计算结果能够看出，当板宽一定时，长度变化对路表弯沉影响不大，长度在达到10.8 m时层底弯拉应力已经收敛不再变化。鉴于模型划分网格的方便，同时兼顾实际模型尺寸，因此本模型选取长度值为31.2 m。

3.4 临界荷位

短路基处AC+CPC复合式路面一般不用设置接缝，但在与其结构物的连接处，仍需要设置接缝，这些接缝为路面的薄弱环节。为确定临界荷位，需要选取路面板不同位置进行试算。在确定模型尺寸为：31.2 m×5.4 m×7 m之后，分别在板角、纵缝边缘中部、横缝边缘中部以及板中部进行标准轴载的加载试算。不同加载位置路面结构应力和变形云图如图9所示，计算结果如图10所示。经过计算CPC层层底的弯拉应力最大，特别是板的纵缝边缘中部和横缝中部位置，所以临界荷位为CPC板的纵缝边缘中部位置。从变形的角度而言，板角位置的弯沉值最大，较纵缝中部和横缝中部位置分别增大了62.5%和41.3%。

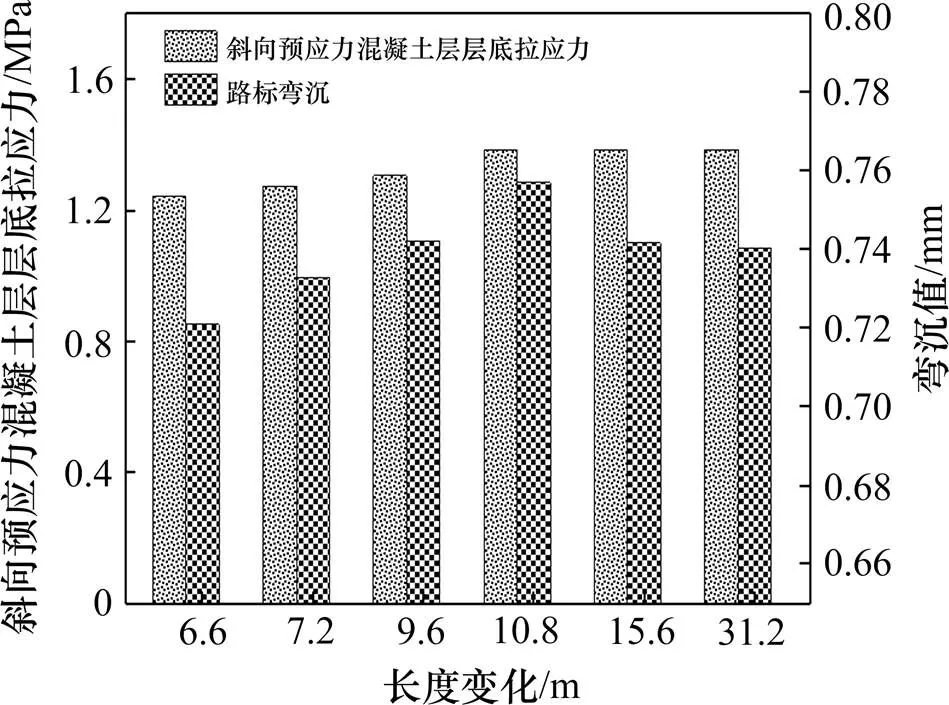
图8 CPC长度取值及其计算结果

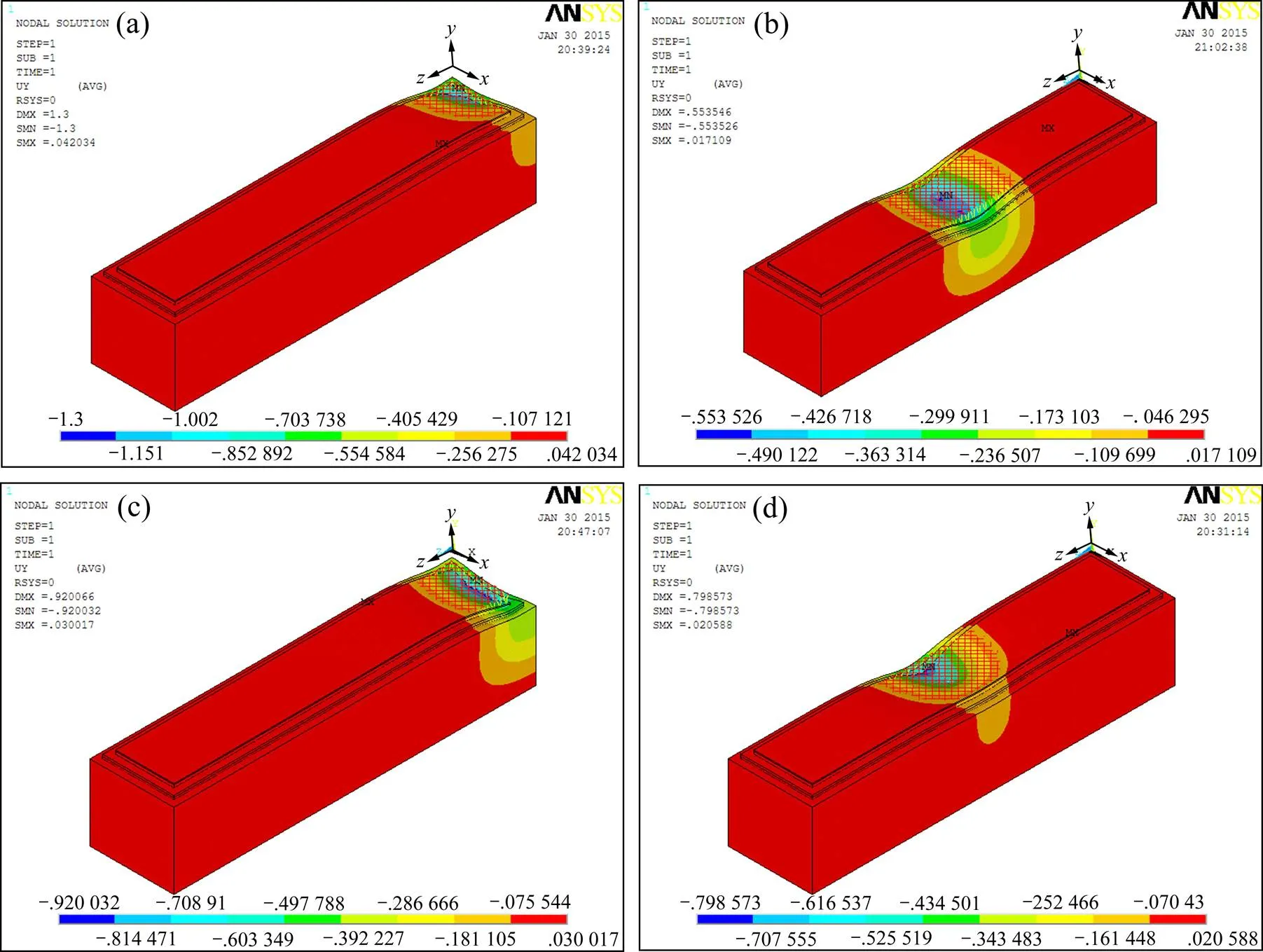
(a) 板角；(b) 板中；(c) 横缝中部；(d) 纵缝中部

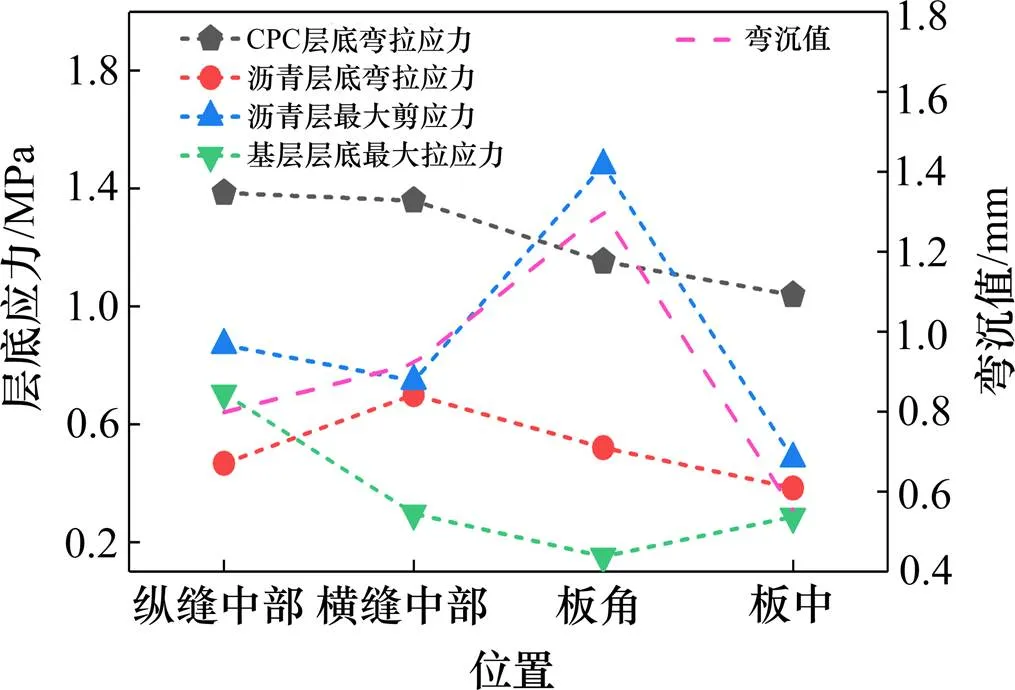
图10 计算结果

4 应力

为了方便复合式路面结构设计，进行有限元模拟时通过变换各结构层的厚度、模量等参数，分析各因素和路面指标之间的联系，通过回归得到回归公式，最后综合得到各个参数的变化和路面指标之间的关系。影响荷载作用下应力响应的因素有轴载，预应力，面层厚度1，水泥混凝土板的厚度2，水泥混凝土板的模量1，基层模量2，地基模量37个因素，因素水平的选取见表2。通过采用均匀设计的方法合理安排参数组合，不仅减少了计算次数而且保证了计算结果的代表性[14]。

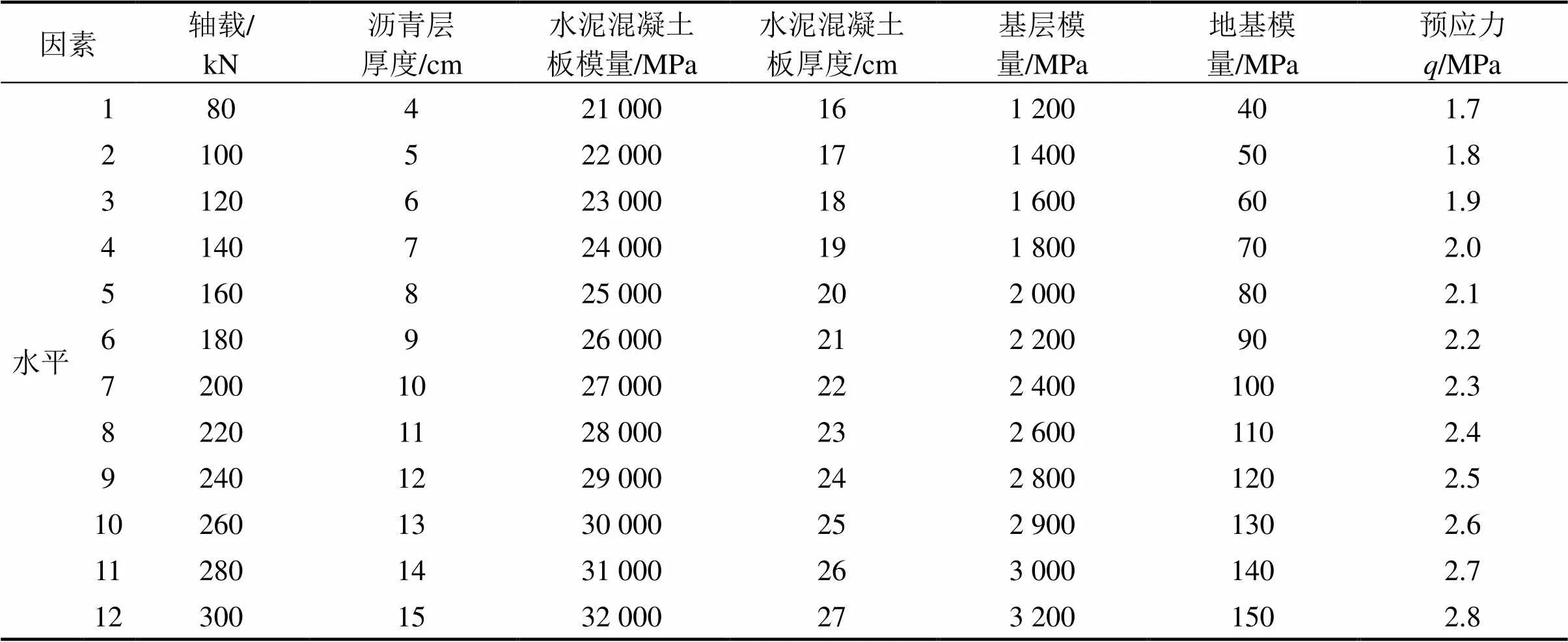
表2 均匀设计中各影响因素及其取值

表3 U12*(1210)均匀设计

为了分析各个因素对荷载作用下应力响应的影响，采用均匀设计表来进行方案的组合设计，影响因素主要如表2所示，运用U*(1210)表来进行设计和使用，分别如表3和表4所示。

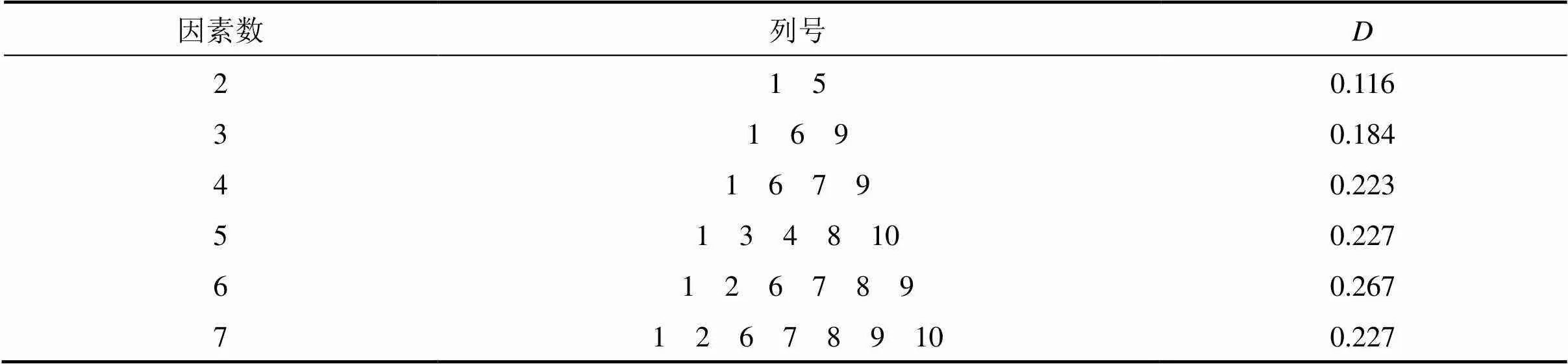
表4 U12*(1210)使用

均匀设计表相对应的均匀设计使用表规定了进行均匀设计计算所需选取的列以及这些列所组成试验方案的均匀度。表3 为U12*(1210)均匀设计表，表4为其使用表。当有2个因素时，应选用1，5列安排试验；若有3个因素，应选用1，6，9列。表示均匀度偏差，其值越小，均匀设计的均匀度愈好。根据表选用均匀设计表中的1，2，6，7，8，9列进行均匀设计计算，根据计算结果进行回归分析，在计算中没有考虑路面结构内部温度对材料参数的影响，即采用的路面各结构层模量大小均为常温状态下的模量值。因此，不考虑路面结构内温度的影响，综合各层厚度、模量及滑动层摩擦因数对混凝土层层底拉应力的计算分析，得出斜向预应力混凝土层底的拉应力回归公式。实践表明二项式回归对于各因素交互作用的情况可以得到较好的效果。因此为了充分考虑各因素之间的相互作用，采用二次多项式进行回归。应用回归软件1stopt对结果进行回归，采用麦考特法和通用全局优化算法，可以得到应力计算公式。回归公式的相关系数=0.994 9，相关系数平方2=0.990 0。该研究只是利用ANSYS有限元软件对AC+CPC复合式路面结构的应力和变形进行分析得到应力计算公式，该公式与实测数据的吻合程度有待进一步实测试验 验证。

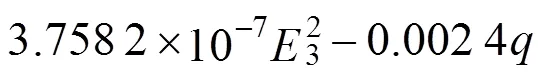
式中：1为斜向预应力混凝土板模量，MPa；2为基层模量，MPa；3为地基模量，MPa；1为沥青层厚度，cm；2为斜向预应力混凝土层厚度，cm；为荷载，kN；为预应力，MPa。

5 结论

1) 对短路基进行了界定，即两桥(隧)之间路基长度少于200 m均可视为短路基。

2) CPC层层底的弯拉应力最大，特别是板的纵缝边缘中部和横缝中部位置，分别为1.385 5 MPa和1.359 4 MPa，所以临界荷位为CPC板的纵缝边缘中部位置。

3) 采用麦考特法和通用全局优化算法，综合各层厚度、模量及滑动层摩擦因数对CPC层层底拉应力的影响，得到了斜向预应力混凝土层层底的拉应力计算公式。

[1] 周娟兰, 郑木莲, 马强, 等. 设应力吸收层的复合式路面反射裂缝扩展路径模拟[J]. 铁道科学与工程学报, 2016, 13(8): 1507−1514. ZHOU Juanlan, ZHENG Mulian, MA Qiang, et al. Simulation of reflection crack propagation path for complex pavement with stress absorbing layer[J]. Journal of Railway Science and Engineering, 2016, 13(8): 1507− 1514.

[2] 张明杰, 祁文洋. 复合式路面与半刚性路面力学响应的对比[J]. 石油沥青, 2016, 30(6): 16−19. ZHANG Mingjie, QI Wenyang. The mechanical response comparison of composite pavement and semi-rigid pavement[J]. Petroleum Asphalt, 2016, 30(6): 16−19.

[3] ZHOU Juanlan, ZHENG Mulian, WANG Chongtao, et al. Dynamic response analysis of road-bridge transition section without slab[J]. International Journal of Pavement Research and Technology, 2017, 10(6): 526−535.

[4] YAO Hui, LI Liang, XIE Hua, et al. Mechanics analysis of vehicle bumping at approach slabs with superelevation[J]. Journal of Southeast University (English Edition), 2012, 28(2): 221−228.

[5] Kim K, Mang Tia, Greene J. Evaluation of structural behavior of precast prestressed concrete pavement with finite element analysis[J]. Transportation Research Record: Journal of the Transportation Research Board, 2016, 2590(1): 84−93.

[6] 刘涛. 重载交通斜向预应力混凝土路面研究[D]. 西安: 长安大学, 2018. LIU Tao. Study on cross-tensioned prestressed concrete pavement under heavy-load transportation[D]. Xi’an: Changan University, 2018.

[7] 张丙强. 考虑层间界面剪切损伤的复合式沥青路面力学特性[J]. 福州大学学报(自然科学版), 2016, 44(4): 588−592. ZHANG Bingqiang. Analysis of mechanical properties for composite asphalt pavement involving shear damage of interface[J]. Journal of Fuzhou University (Natural Science Edition), 2016, 44(4): 588−592.

[8] 建技[2003]97号, 提高铁路路基工程设计、施工质量补充规定[S]. Jianji[2003] No.97, Supplementary provisions to improve the railway subgrade engineering design and quality[S].

[9] 郑木莲, 孟建党, 张世铎, 等. 路桥过渡段上车内人体舒适性评价方法[J]. 长安大学学报(自然科学版), 2012, 32(2): 1−6. ZHENG Mulian, MENG Jiandang, ZHANG Shiduo, et al. Evaluation method of human comfort in vehicle at transition section between bridge abutment and embankment[J]. Journal of Chang’an University (Natural Science Edition), 2012, 32(2): 1−6.

[10] Thiele D J, Tadros M K, Benak J V. State of the art for control of bridge approach settlement[C]// In: Bridge Evaluation Repair and Rehabilitation. USA. Kluwer Academic Publishers, 1990: 57−70.

[11] 冉武平, 张玉, 李爽. 沥青路面层间接触状态研究进展[J]. 重庆交通大学学报(自然科学版), 2019, 38(8): 45−52. RAN Wuping, ZHANG Yu, LI Shuang. Research progress on interlayer contact state of asphalt pavement[J]. Journal of Chongqing Jiaotong University (Natural Science), 2019, 38(8): 45−52.

[12] XU Yongli, RAN Wuping, ZHANG Yu, et al. Mechanical characterisation of interface shear strain of multi-layer composite pavement[J]. International Journal of Pavement Engineering, 2019: 1−7.

[13] 丁彦昕. 浅议公路桥头跳车的成因与防治[J]. 公路交通科技, 2002, 19(5): 92−93, 98. DING Yanxin. Causes and prevention of bumping at bridge-head[J]. Journal of Highway and Transportation Reseach and Development, 2002, 19(5): 92−93, 98.

[14] 陈忠平, 王树林. 气泡混合轻质土及其应用综述[J]. 中外公路, 2003, 23(5): 117−120. CHEN Zhongping, WANG Shulin. Summary of bubble mixed light soil and its application[J]. Journal of China & Foreign Highway, 2003, 23(5): 117−120.

Stress response analysis of AC+CPC composite pavement at short subgrade subjected to loading action

ZHENG Mulian1, LIU Fuqiang1, WANG Tao2, WANG Shuai3

(1. Key Laboratory of Highway Engineering in Special Region, Ministry of Education Chang’an University, Xi’an 710064, China; 2. School of Civil Engineering Beijing Jiaotong University, Beijing 100044, China; 3. CCCC Highway Consultants Co., Ltd., Beijing 100032, China)

In order to study the stress response of oblique prestress reinforced concrete overlying asphalt layer (AC+CPC) composite pavement at short subgrade subjected to loading action, the AC+CPC composite pavement at short subgrade was taken as the research object. The three-dimensional finite element model of AC+CPC composite pavement was established by ANSYS finite element software, and the stress response of AC+CPC composite pavement at short subgrade subjected to loading action was analyzed. Results show that the length of short subgrade between two bridges (tunnels) is defined to be less than 200 m. The flexural stress at the bottom of CPC layer is the largest, especially the middle of longitudinal seam edge and horizontal seam, which are 1.385 5 MPa and 1.359 4 MPa respectively. It can be known that the critical load place of AC+CPC composite pavement at short subgrade is the middle of longitudinal seam edge. The calculation formula of the tensile stress at the bottom of CPC layer is obtained using the McCott method and the general global optimization algorithm.

short subgrade; composite pavement; AC+CPC; stress; finite element

10.19713/j.cnki.43−1423/u.T20200585

U416

A

1672 − 7029(2021)04 − 0926 − 08

2020−06−23

陕西省交通科技项目(13-04K)

郑木莲(1977−)，女，山东蒙阴人，教授，从事道路工程结构与材料研究；E−mail：zhengml@chd.edu.cn

(编辑 涂鹏)