节段模型弹性悬挂系统的阻尼非线性对涡激力模型参数识别结果的影响

陈政清，肖潇，黄智文，华旭刚

节段模型弹性悬挂系统的阻尼非线性对涡激力模型参数识别结果的影响

陈政清1, 2，肖潇1, 2，黄智文1, 2，华旭刚1, 2

(1. 湖南大学 风工程与桥梁工程湖南省重点实验室，湖南 长沙 410028；2. 湖南大学 振动与冲击技术研究中心，湖南 长沙 410028)

通过耗能相等的原理给出系统等效阻尼比的表达式，分析节段模型弹性悬挂系统固有阻尼比的振幅依赖性对涡激力参数识别的影响。以Scanlan非线性涡激力模型为例，通过求解弹性悬挂系统的非线性运动方程得到节段模型涡振振幅随时间的变化曲线，并进一步说明考虑阻尼比振幅依赖性下的涡激力参数识别方法。在考虑节段模型阻尼比随振幅线性变化的情况下分别识别一种具有Rayleigh形式的非线性涡激力模型参数和Scanlan非线性涡激力参数，并将两者的识别结果进行对比。最后说明节段模型阻尼比的测量误差对非线性涡激力识别结果的影响。研究结果表明：节段模型悬挂系统的涡振幅值同时受到气动参数和系统非线性阻尼比的影响，气动力参数可以通过测振试验来识别；Rayleigh型非线性涡激力模型与Scanlan非线性涡激力模型之间在涡振振幅稳定时存在明显的差异，但这种差异不会影响涡振位移响应预测；考虑结构固有阻尼比的振幅依赖性之后，阻尼比的识别误差对涡激力参数识别结果的影响会相应减小。

涡激振动；参数识别；桥梁；节段模型；振幅依赖性

主梁涡激共振是大跨度桥梁在常遇风速下容易发生的一种风致振动现象[1]。涡激共振虽然不像颤振一样会在短时间内导致整体结构的毁灭性破坏，但过大的振幅和加速度会严重影响桥梁的使用功能，频繁发生的涡振还可能引起构件的疲劳破坏[2]。因此在大跨度桥梁抗风设计阶段准确预测主梁的涡振响应，并研究必要的涡振控制措施是桥梁抗风研究的重要课题。目前，实桥涡振响应预测主要采用弹性悬挂节段模型风洞试验和理论分析相结合的方法。弹性悬挂节段模型风洞试验采用刚体模型，不能考虑实桥振型对涡激力分布的影响。为了准确预测实桥涡振响应，一个必要的技术环节就是通过节段模型风洞试验识别和建立主梁的涡激力数学模型。涡激力数学模型的种类很多，但在桥梁风工程领域研究最多的还是以Scanlan非线性涡激力模型[3]为代表的单自由度涡激力模型。近年来，很多学者对Scanlan非线性涡激力模型的适用性进行了研究，并在此基础上提出了很多新的非线性涡激力模型。ZHU等[4]利用内置天平同步测力测振技术较精确地测量了一个大比例扁平箱梁节段模型上的涡激力，并基于涡激力的测试结果提出了一种Rayleigh型非线性涡激力模型。在此基础上，ZHU等[5]研究了紊流场中节段模型上的涡激力，并进一步改进了Rayleigh型涡激力模型。Marra等[6]研究了Scruton数(Sc数)对4:1矩形断面涡振响应的影响，揭示了Scanlan非线性涡激力模型的气动参数与Sc数的关系，并对Scanlan非线性涡激力模型及参数识别方法进行了完善。XU等[7]提出了一种广义瑞利型多项式涡激力模型，可以较好地预测不同Sc数下节段模型的涡振响应。张明杰[8]提出了一种基于描述函数的涡激力模型，并分析了该模型对主梁竖向和扭转涡振响应的预测效果。上述非线性涡激力模型都是半经验性的，其气动参数必须采用节段模型风洞试验识别。自由振动法是目前使用最多的涡激力模型参数识别方法，它首先通过涡振锁定风速区间的自由振动试验获得节段模型从瞬态到稳态的涡振响应，然后通过比较涡激力模型预测的理论涡振响应和风洞试验结果实现参数识别。针对Scanlan非线性涡激力模型，Marra等[9]提出了一种基于单纯形优化算法的参数识别方法，该方法首先假定1和的迭代初始值，然后以数值积分反算的节段模型瞬态涡振位移响应与对应实验数据差值的平方和最小值作为目标函数对1和进行迭代求解[10]。对于非线性涡激力模型，节段模型涡振响应的理论解一般通过谐波平衡法等近似解析算法或龙格库塔法等数值积分方法求解。无论采用哪种方法，都需要先准确识别节段模型弹性悬挂系统的动力特性，特别是阻尼特性。在有关涡激力数学模型及其参数识别的研究中，大部分文献都假定节段模型弹性悬挂系统的阻尼是线性的。实际上，结构阻尼的非线性是普遍存在的，只是在不同的结构中阻尼非线性有强弱之别。近年来，已经有学者开始关注节段模型弹性悬挂系统阻尼的非线性特性。GAO等[11-12]对节段模型弹性悬挂系统的固有阻尼进行了识别，结果表明该阻尼具有明显的非线性，非线性的强弱与节段模型采用的阻尼措施有关，但一般都可表示为节段模型无量纲振幅的函数，忽略阻尼比的振幅依赖性会导致节段模型自由振动响应预测失真。在此基础上，ZHANG等[13]进一步分析指出节段模型弹性悬挂系统的非线性阻尼主要来自振动过程中节段模型与风洞周围空气的流固耦合作用。基于上述研究，近年来有学者开始在涡激力、驰振力和颤振力等非线性气动力模型参数识别中考虑节段模型弹性悬挂系统的阻尼非线性[14-17]，但没有开展系统分析。为了揭示节段模型弹性悬挂系统固有阻尼的非线性对涡激力模型气动参数识别结果的影响，本文假定节段模型弹性悬挂系统的非线性固有阻尼可等效表示为依赖于模型振幅的可变阻尼比，然后分别以Rayleigh型非线性涡激力模型和Scanlan非线性涡激力模型为例，阐述了非线性固有阻尼条件下上述涡激力模型气动参数的识别方法，并对比了二者的识别结果，最后分析了弹性悬挂系统固有阻尼比的识别误差对参数识别结果的影响。

1 节段模型弹性悬挂系统阻尼的非线性特性

当考虑节段模型弹性悬挂系统的阻尼非线性时，节段模型的涡振运动方程可表示为

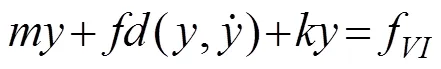
节段模型弹性悬挂系统的阻尼主要来自模型连接部位的摩擦、螺旋弹簧的材料阻尼、以及节段模型与周围空气的流固耦合作用[13]。对于节段模型弹性悬挂系统这样的弱非线性系统，采用依赖于模型振幅的等效阻尼比进行一阶近似往往就可以达到足够的精度。广义的阻尼力模型可表示为[18−19]

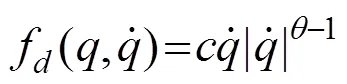
虽然节段模型弹性悬挂系统的阻尼来源复杂，但通过总结相关文献[18-19]可以发现，综合采用库伦阻尼力、线性黏滞阻尼力和二项式阻尼力模型来描述其阻尼特性就可达到较高的近似精度，即

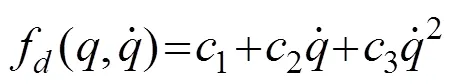
节段模型在自由振动和涡振时都表现为准简谐振动，因此可以根据耗能相等的原理，采用与振幅相关的等效阻尼比近似表示式(3)所示的弹性悬挂系统的阻尼效应。对于一般的广义阻尼力模型(2)，其等效阻尼比可以表示为

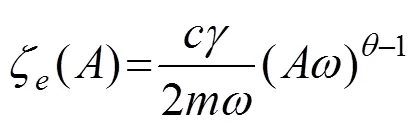
其中表示悬挂系统振幅。式(4)中的表达式可以表示为

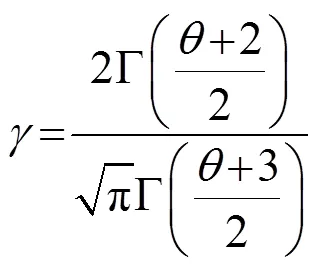
其中Γ(.)表示gamma函数。

分别令(4)和(5)中的=0, 1, 2后，代入到悬挂系统阻尼力模型式(3)后，悬挂系统的运动方程可以改写为

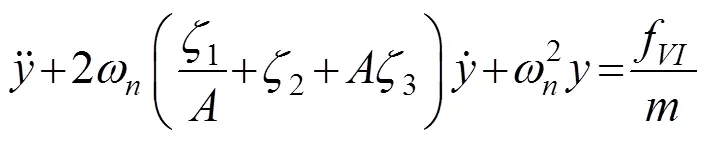
方程(6)给出了考虑悬挂系统阻尼比的振幅依赖性后，系统在涡激力作用下的运动方程。本文接下来拟以Scanlan非线性涡激力模型[3]以及Rayleigh型涡激力数学模型[4]为例来说明这种情况下涡激力参数的识别方法。

2 Scanlan非线性模型气动参数识别

Scanlan非线性涡激力模型可以表示为[3]

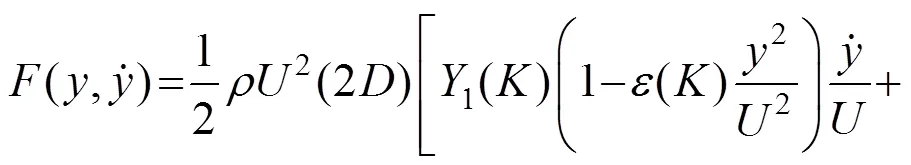
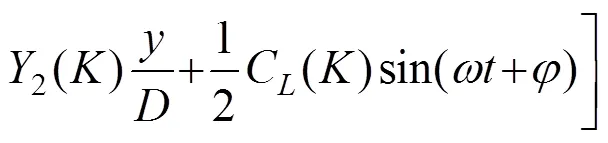
其中：和分别表示来流空气密度和速度；表示节段模型的特征长度，通常取模型高度；表示漩涡脱落频率；=/表示折减频率；­1表示线性气动阻尼系数；表示非线性气动阻尼系数；2表示线性气动刚度系数；C和分别表示强迫力系数以及强迫力与结构位移的相位差。1,2,C,均为折减频率的函数，且都需要在风洞试验中进行 识别。

文献表明[20]，在涡振锁定区间Scanlan非线性涡激力模型可以简化为

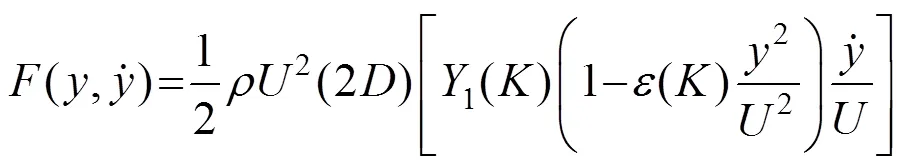
将式(8)代入到悬挂系统运动方程式(1)后，可以得到悬挂系统在Scanlan非线性涡激力模型作用下的无量纲运动方程为

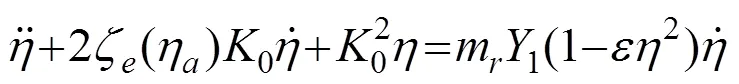
其中：()=()/代表节段模型竖向的无量纲位移响应；=/表示无量纲时间；m=2/表示质量比；0=ωD/表示节段模型的无量纲固有频率；ω表示弹性悬挂系统的固有频率；ζ(η)表示弹性悬挂系统的等效阻尼比，对应的表达式为

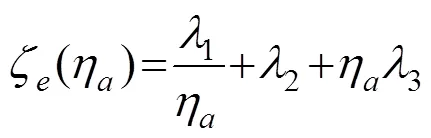
1=1/,2=2,3=3；η表示在涡振锁定区间内节段模型的瞬态无量纲响应幅值，η的表达式为

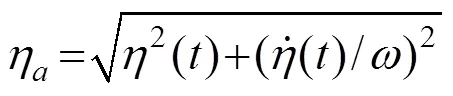
将式(11)和式(10)代入到式(9)后，式(9)可以改写为

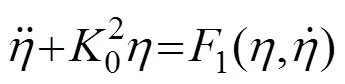
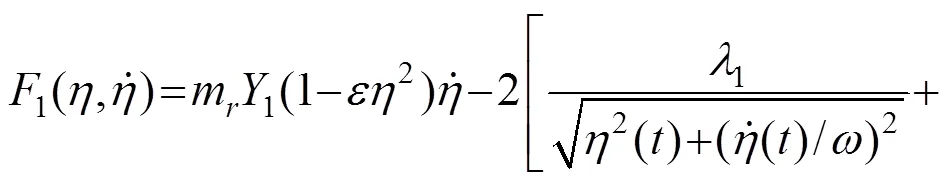
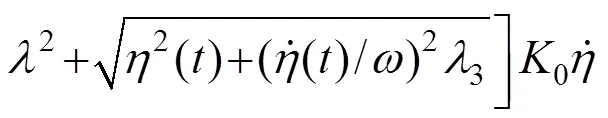
式(12)给出了一个自治非线性微分方程，其一阶近似解析解可以表示为[21]

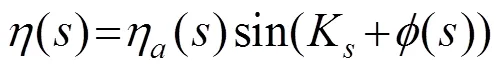
根据缓变函数理论，悬挂系统振幅可以由以下一阶微分方程近似表示

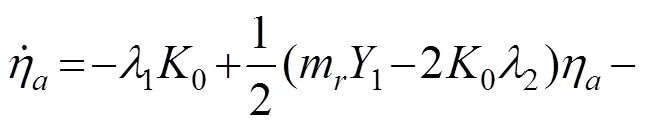
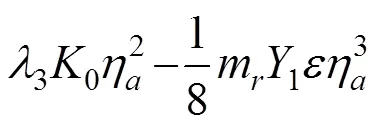
式(15)为一元一阶三次非齐次微分方程，尽管存在解析解，但是解析解的数学表达式十分复杂，因此必须通过数值积分得到η的时程变化曲线。

从式(15)可以看到，节段模型系统在涡激力作用下的位移响应包络线同时受气动参数1,和悬挂系统阻尼参数1,2,3的影响。忽略结构固有阻尼比的振幅依赖性必然会导致结构响应求解的错误，基于节段模型瞬态涡振位移响应的参数识别也会随之出现偏差。

考虑了悬挂系统阻尼比的振幅依赖性之后，涡激力气动参数的识别可以通过从试验模拟数据出发，采用直接搜索优化算法来对气动参数进行迭代求解，识别流程如图1所示。值得指出的是，图1所示流程图不仅仅适用于Scanlan涡激力模型中气动参数1和的识别，对于其他涡激力模型的参数识别同样适用。

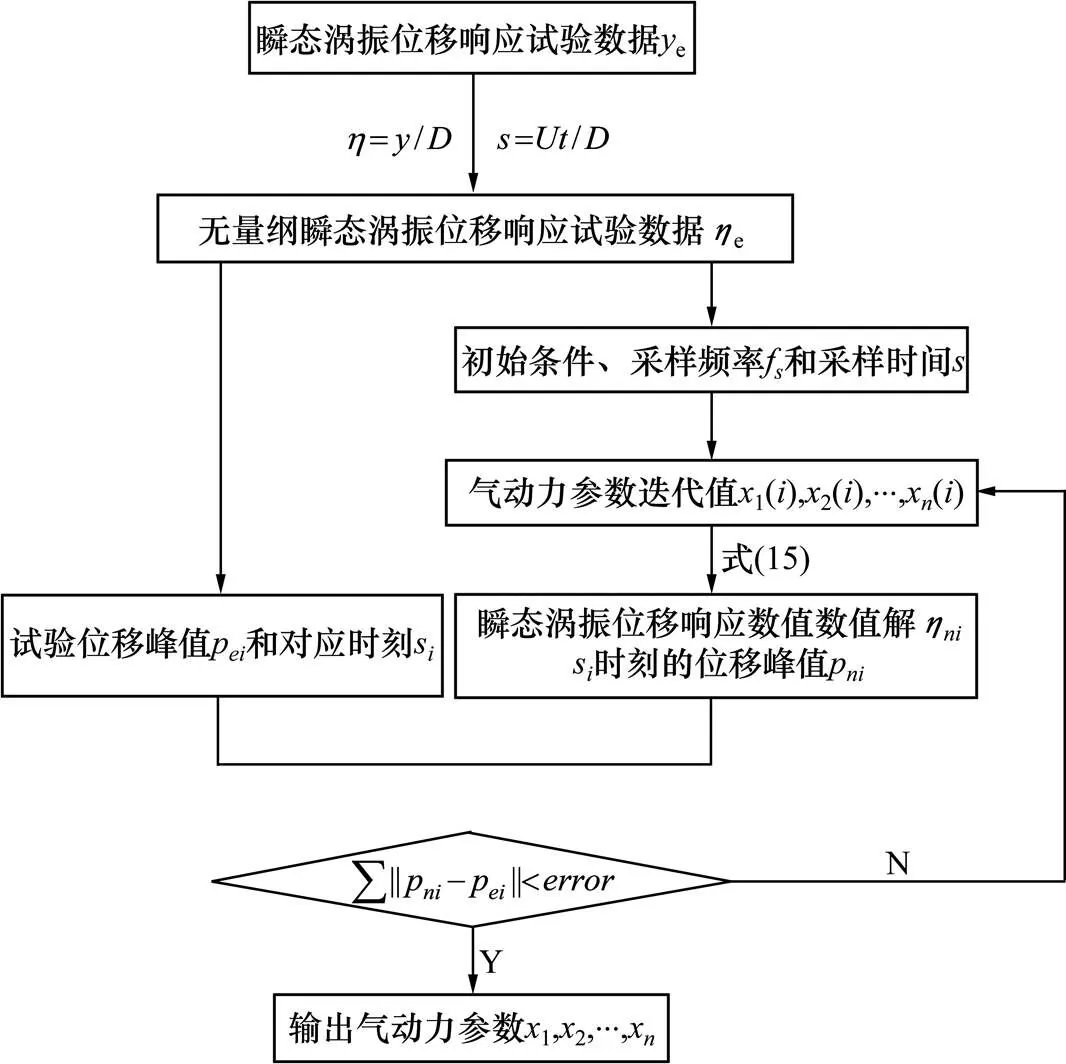
图1 涡激力气动参数识别流程

3 Rayleigh型非线性涡激力模型气动参数识别

ZHU等[4]所提出的Rayleigh型非线性涡激力模型表达式为：

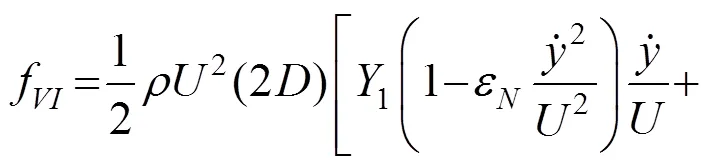
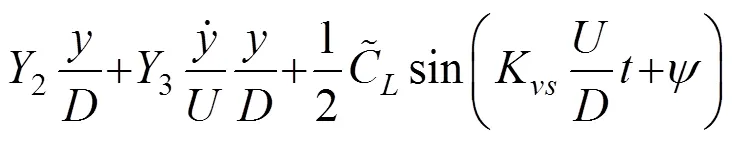
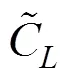
文献[4]的分析表明在涡激共振的主要锁定区间内，式(16)中的强迫力项可以忽略，气动刚度项和速度位移交叉项在一个振动周期内对结构 所做的功为0，也可以不考虑，所以原模型可以简 化为[22]，

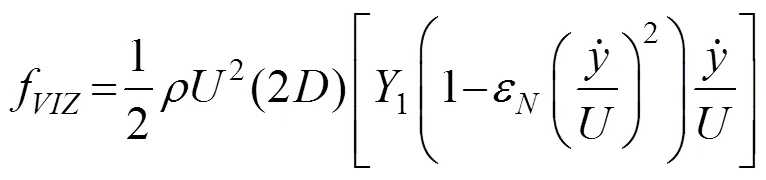
可以看到，式(17)具有Rayleigh方程的形式，只有线性气动阻尼参数1和非线性气动阻尼参数ε2个气动参数。与Scanlan模型相比，二者只在涡激力的非线性项上存在差别。

把式(17)代入式(1)，得到节段模型振动系统在核心涡激力模型作用下的无量纲运动方程：

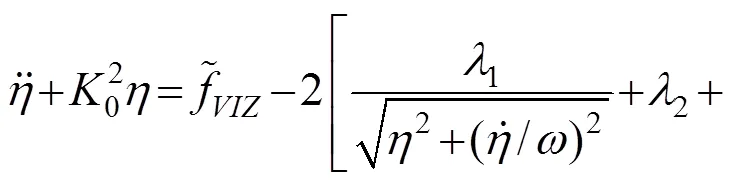
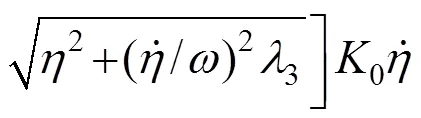
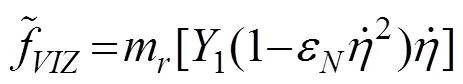
通过与第2节进行类似的推导，可以得到式(18)中节段模型的振幅随时间变化的关系为

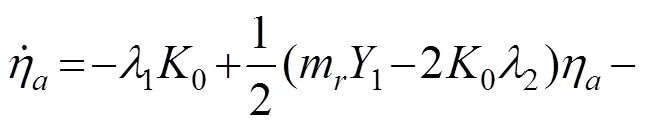
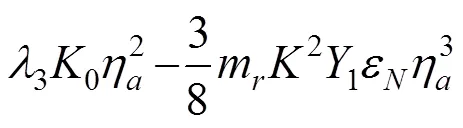
比较式(20)和式(15)可知，二者的差别仅在于等式右边的最后一项。因此如果分别采用Rayleigh型非线性涡激力模型和Scanlan非线性模型对相同的试验数据进行参数识别，那么识别结果之间必然存在如下关系：

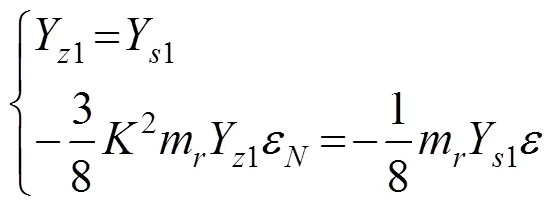
进一步化简式(21)后，可以得到：

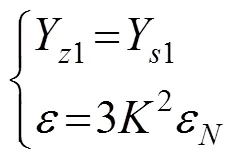
4 算例分析

算例分析的原始数据来源于文献[4]，其中节段模型的高度=0.175 m，考虑非风致附加质量在内的单位长度质量=56.236 kg/m，质量比r=6.671 1×10−4，固有频率0=2.808 Hz。自由振动衰减试验发现节段模型振动系统的固有阻尼比具有振幅依赖性，可表示为

如果采用常阻尼拟合上述自由衰减的试验数据，得到节段模型悬挂系统的名义固有阻尼比为0.5%。

当风速=9.1 m/s时，文献[4]根据涡激力时程直接识别得到Rayleigh型非线性涡激力模型的气动参数为1=11.966,ε=103.361。根据以上气动力参数和结构参数，在给定初始位移和速度的条件下，可以通过求解节段模型的涡振运动方程可得模型的瞬态涡振位移响应时程，如图2所示(下文中简称模拟试验数据)。

通过模拟试验数据，对Rayleigh型非线性涡激力模型的气动参数1和ε­进行了识别，识别过程如图1所示，用于参数识别的数据总长度=416 0。识别结果为1=11.941，ε=104.841，与文献[4]直接从涡激力时程进行参数识别的结果非常相近。把识别结果代入节段模型涡振运动方程(18)和(19)，求解得到的节段模型瞬态位移响应包络线与模拟试验数据的比较如图3所示。可以看到，无论是在起振阶段，还是在振动稳定状态，数值计算结果与模拟实验数据都相当吻合，这说明识别结果是准确的，并证明了在准确描述节段模型阻尼特性的条件下通过测振试验就能识别Rayleigh型非线性涡激力模型的气动参数。

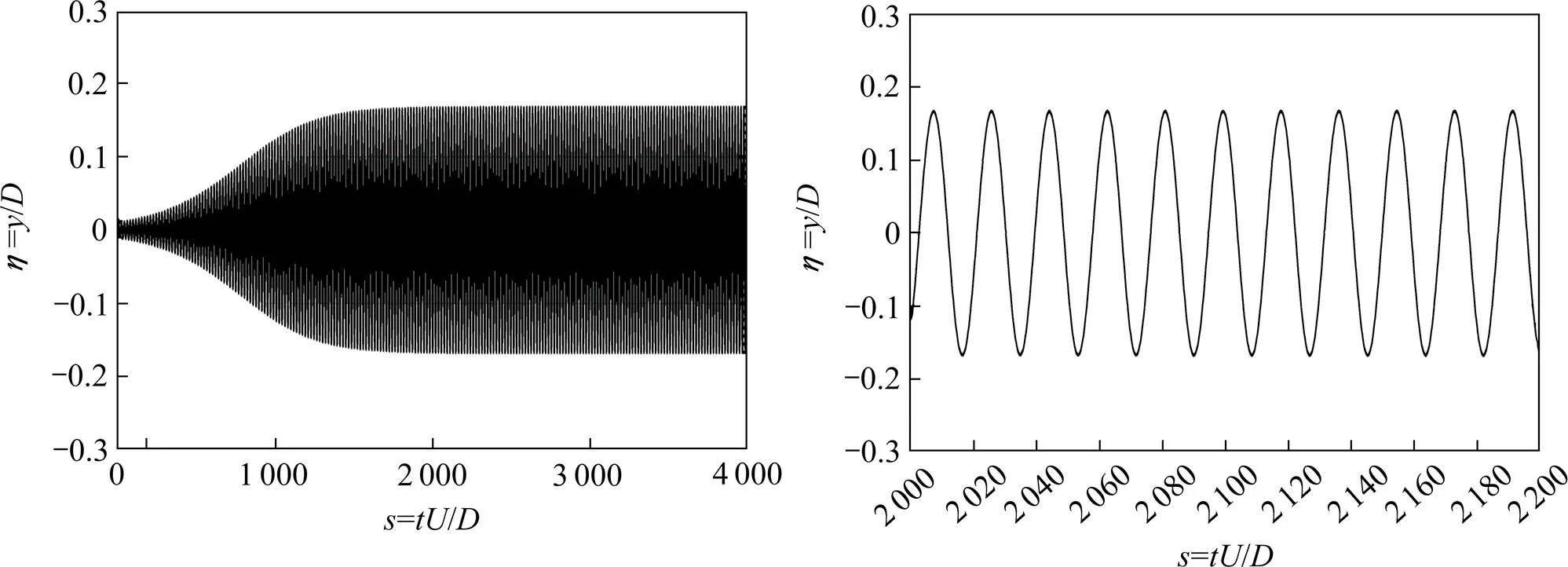
图2 节段模型瞬态涡振位移响应时程

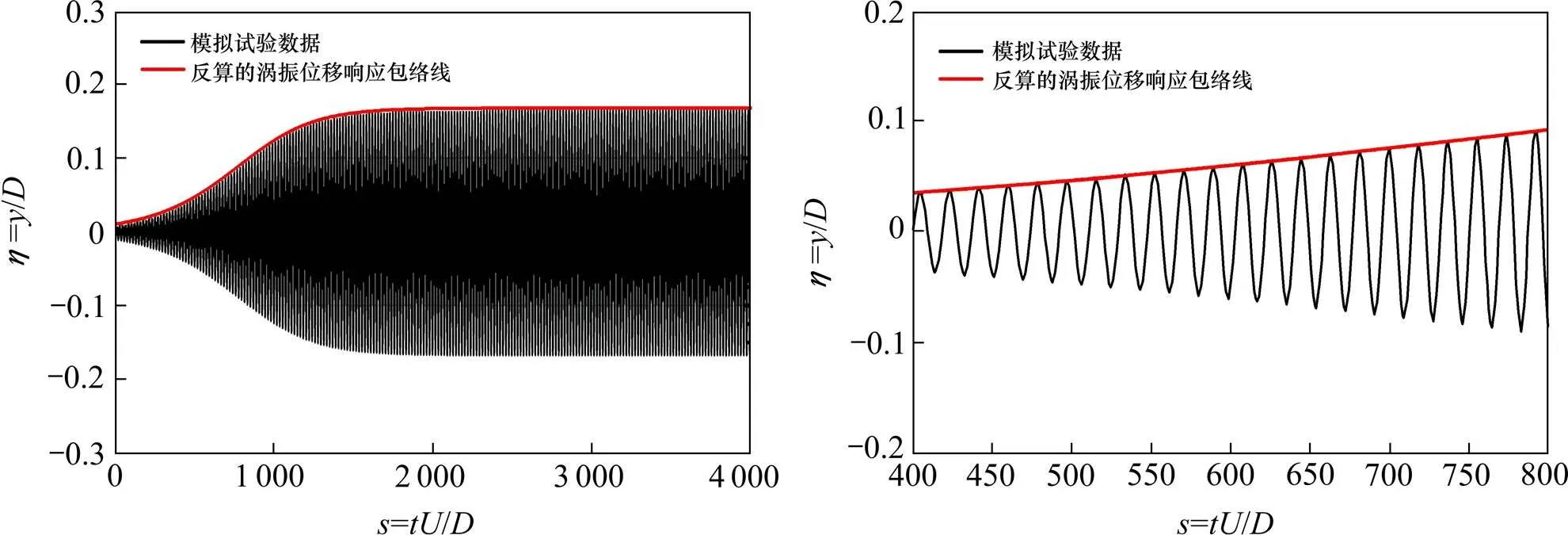
图3 Rayleigh型非线性涡激力模型识别结果验证

由于Scanlan模型中的气动参数和Rayleigh型非线性涡激力模型中的气动参数之间满足式(22)。因此，在图2所给出的模拟试验数据中，可以得到Scanlan非线性模型的气动参数为s1=11.941和=104.841×3×0.342=36.359。为了对此进行验证，采用图1所示的流程图和方程(15)对Scanlan非线性模型进行了参数识别，结果为1=11.941，=36.363。可以看到，实际参数识别的结果与预测结果完全吻合。因此从涡振位移响应预测的角度看，Scanlan非线性涡激力模型与Rayleigh型模型是等效的。图4比较了根据参数识别结果反算的Rayleigh型非线性涡激力和Scanlan非线性涡激力。可以看到，在涡激振动的稳定状态Scanlan非线性涡激力与Rayleigh型涡激力存在显著的差别。为了对上述差异的影响进行分析，可以直接计算二者之间的差值D，

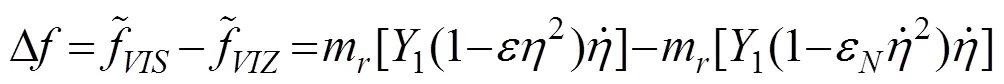
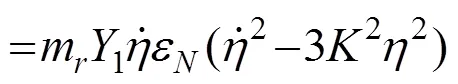
把式(14)代入式(24)，进一步化简可得

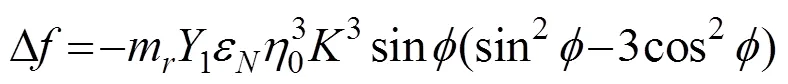
D在一个周期内对节段模型所做的功为

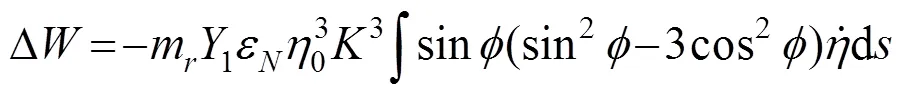
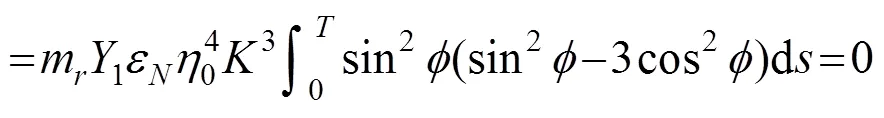
由此可以看到，2种涡激力的差值项在一个周期内对节段模型所作的功为0，故在进行结构涡振位移响应的预测时，通过识别所得到的Scanlan非线性涡激力与真实涡激力之间的差异并不会对结构涡振位移响应的预测造成影响。

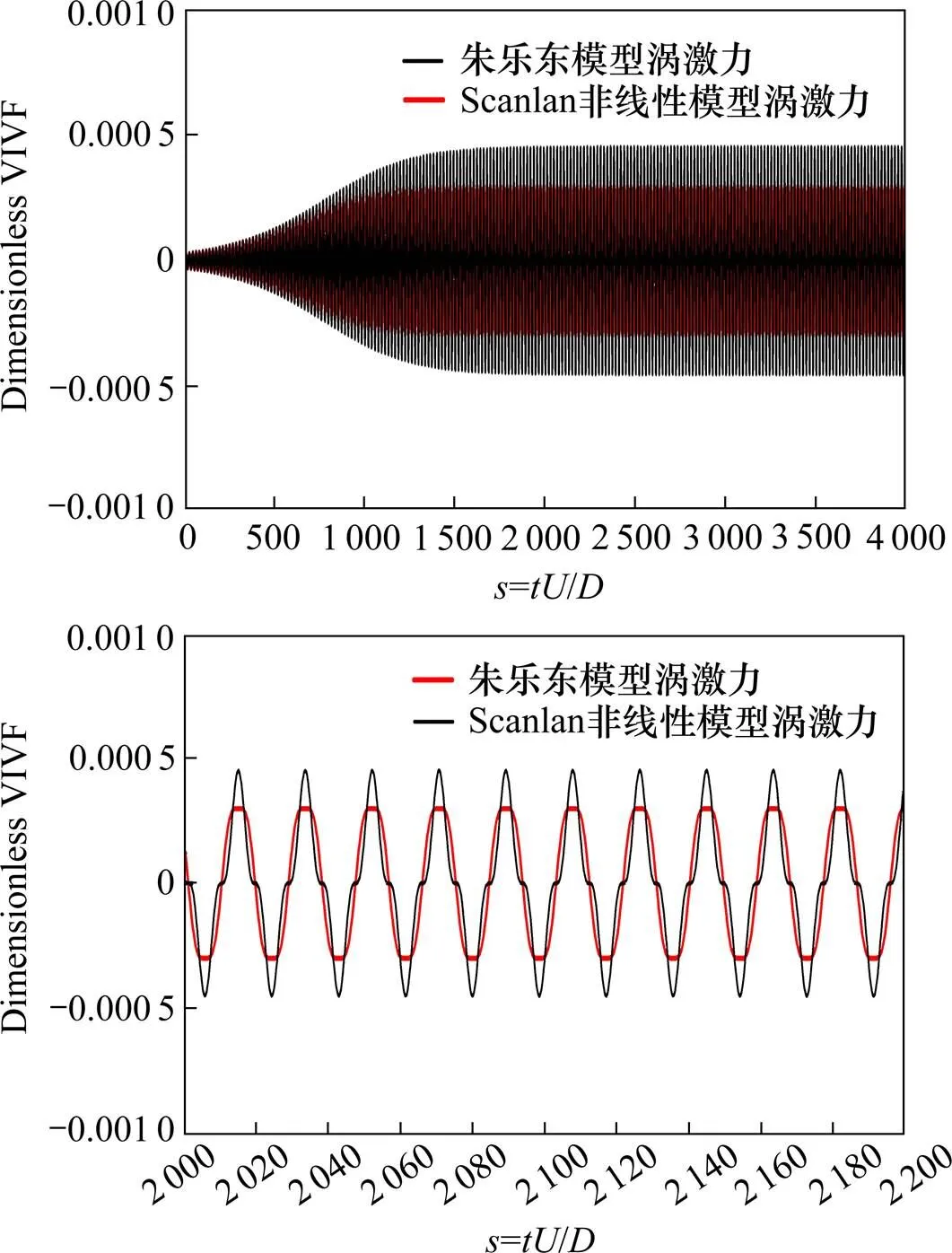
图4 通过识别参数反算的Rayleigh型非线性涡激力和Scanlan非线性涡激力

5 固有阻尼比识别误差的影响

考虑到Scanlan非线性模型的参数识别结果和Rayleigh型非线性涡激力模型的识别结果之间存在特定的数学关系，所以这里仅以Scanlan非线性模型为例讨论弹性悬挂节段模型固有阻尼比的识别误差对涡激力模型参数识别结果的影响。根据第1节得到的模拟试验数据，当节段模型的涡激共振达到稳定时其无量纲涡振振幅为η=0.167 7，此时节段模型振动系统的固有阻尼比为=0.052 76η+ 0.001 58=0.008 75。下面假设2种不能正确考虑节段模型固有阻尼比与振幅之间依赖关系的工况。

5.1 常阻尼比假定引起的识别误差

当采用自由振动衰减试验来识别弹性悬挂节段模型的固有阻尼比时，通常选择包含多个衰减振动周期的数据来计算结构阻尼比，这实际上假定了节段模型的固有阻尼比为常阻尼比，而忽略了可能存在的阻尼比的振幅依赖性。针对这一情况，本文假设自由振动衰减试验识别得到的常阻尼比为0.003，0.005，0.007，0.008 75，0.009，0.011和0.013，从第1节的模拟试验数据出发，根据图3所示的流程图对Scanlan非线性模型进行参数识别，结果如图5所示。可以看到，如果把固有阻尼比当做常阻尼比来处理，那么无论常阻尼比取何值气动参数1和的识别结果都会严重偏离正确值。此外，随着常阻尼比的增加，1的识别结果线性增大，而则沿缓和曲线减小，这与Eshan在文献[20]中针对常阻尼比情况下推导出的1和的识别公式(如式(27)和式(28)所示)相吻合，从而从侧面说明了本文识别方法的正确性。

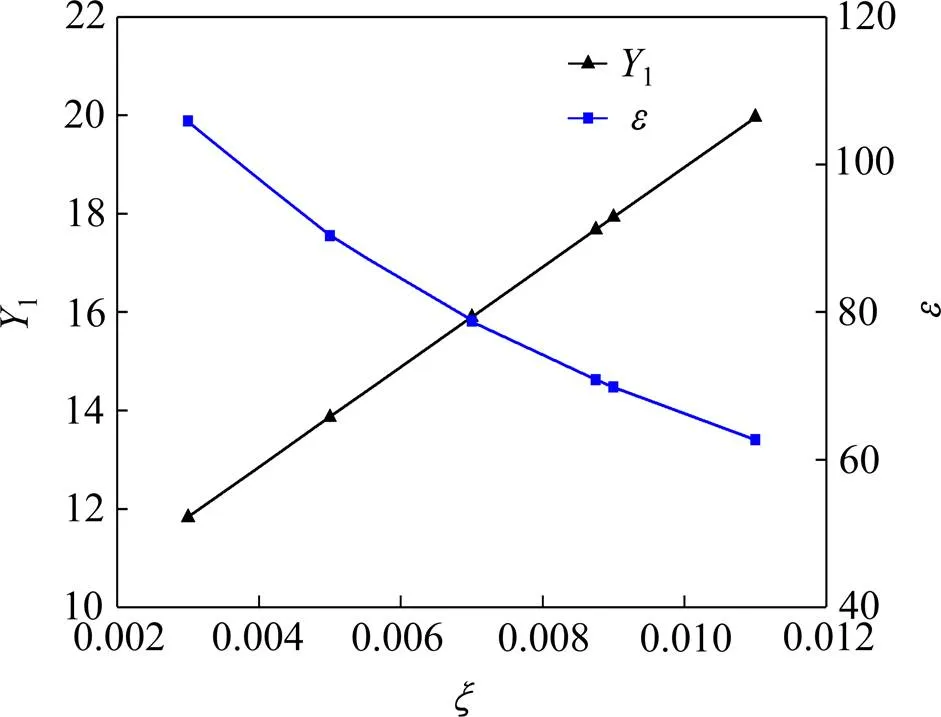
图5 常阻尼下Scanlan非线性模型参数识别

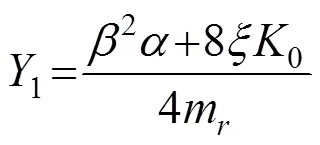
5.2 阻尼参数偏差引起的识别误差

固有阻尼比的识别精度会受到噪声信号和识别方法等的影响。为了考虑这一因素，下文中假设固有阻尼比随振幅变化的表达式中常数项或一次项的识别存在误差，其中常数项考虑以下取值：=0，0.001，0.001 58，0.002，0.003，0.004，其中0.001 58为真实值；一次项取：=0.01，0.02，0.03，0.04，0.042 76，0.05，0.06，其中0.042 76为真实值。以上2种情况气动参数识别的结果分别如图6和图7所示。可以看到，常数项和一次项的识别误差都会对1和的识别结果造成影响，而且这种影响都是接近线性的。相比1，固有阻尼比的识别误差对的影响更大；而相比常数项，一次项的识别误差对的识别影响更大。

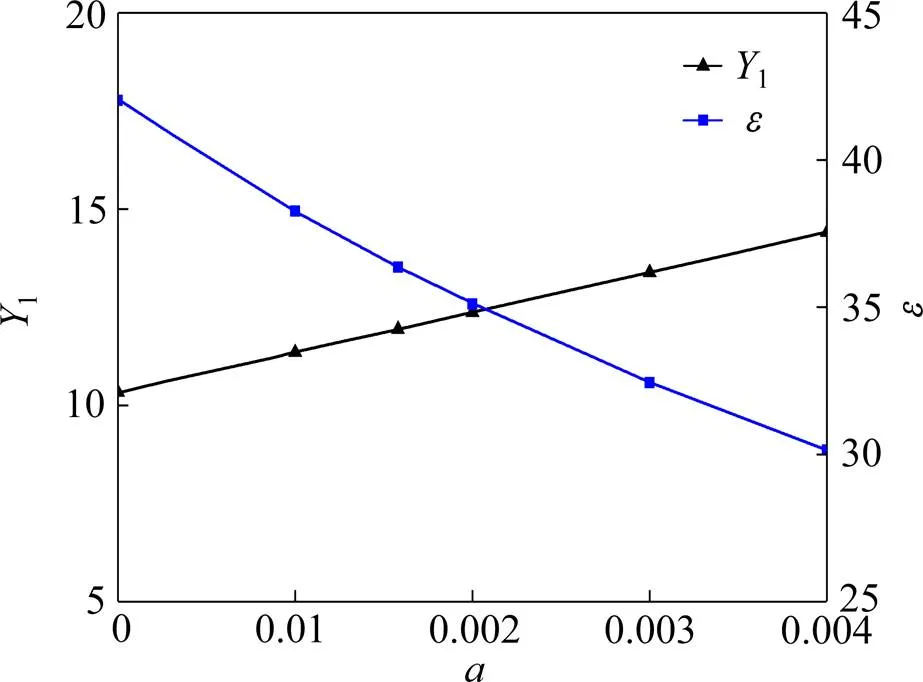
图6 常数项变化

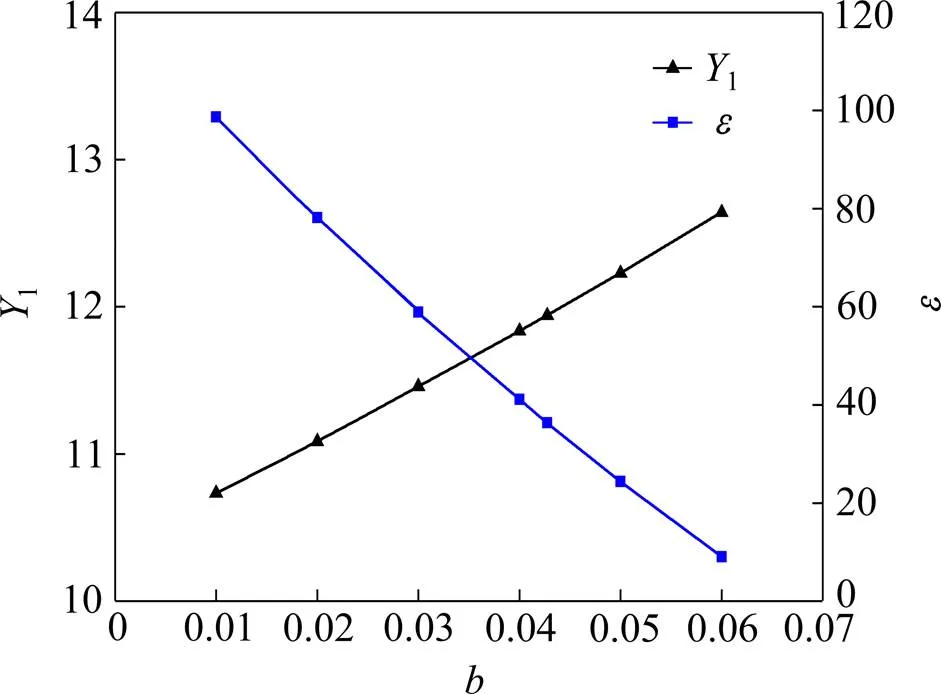
图7 一次项变化

综上所述，准确识别弹性悬挂节段模型的固有阻尼比是保证涡激力模型气动参数识别准确性的前提。如果节段模型振动系统的固有阻尼比具有明显的振幅依赖性，那么在进行气动参数识别时就必须加以考虑，否则识别结果将存在较大的误差。

6 结论

1) 在识别弹性悬挂节段模型系统的固有阻尼比时需要特别注意振动系统的固有阻尼比是否存在振幅依赖性，忽略这种非线性而进行涡激力参数识别，会得到错误的识别结果。

2) 在准确识别节段模型固有阻尼比的条件下，利用直接搜索优化算法能够仅通过测振试验就能识别Scanlan非线性涡激力模型和Rayleigh型非线性涡激力模型的气动参数。

3) 从涡振位移预测的角度看，Scanlan非线性涡激力模型与Rayleigh型非线性涡激力模型等效。

[1] 陈政清. 桥梁风工程[M]. 北京: 人民交通出版社, 2005.CHEN Zhengqing. Bridge wind engineering[M]. Beijing: China Communication Press, 2005.

[2] 葛耀君, 赵林, 许坤. 大跨桥梁主梁涡激振动研究进展与思考[J]. 中国公路学报, 2019, 32(10): 1−18.GE Yaojun, ZHAO Lin, XU Kun. Review and reflection on vortex-induced vibration of main girders of long-span bridges[J]. China Journal of Highway and Transport, 2019, 32(10): 1−18.

[3] Simiu E, Scanlan R H. Wind effects on structures: fundamentals and applications to design[M]. John Wiley, 1996.

[4] ZHU L D, MENG X L, GUO Z S. Nonlinear mathematical model of vortex-induced vertical force on a flat closed-box bridge deck[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2013, 122: 69−82.

[5] ZHU Q, XU Y L, ZHU L D, et al. A semi-empirical model for vortex-induced vertical forces on a twin-box deck under turbulent wind flow[J]. Journal of Fluids & Structures, 2017, 71: 183−198.

[6] Marra A M, Mannini C, Bartoli G. Measurements and improved model of vortex-induced vibration for an elongated rectangular cylinder[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2015, 147: 358−367.

[7] XU K, GE Y, ZHAO L, et al. Calculating vortex-induced vibration of bridge decks at different mass-damping conditions[J]. Journal of Bridge Engineering, 2018, 23(3): 04017149.1−04017149.15.

[8] 张明杰. 桥梁主梁非线性气动力和风振响应特性研究[D].大连: 大连理工大学, 2019. ZHANG Mingjie. Nonlinear aerodynamics and wind- induced vibrations of bridge decks[D]. Dalian: Dalian University of Technology, 2019.

[9] Marra A M, Mannini C, Bartoli G. Van der pol-type equation for modeling vortex-induced oscillations of bridge decks[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2011, 99(6): 776−785.

[10] Marra A M. Risk assessment of bridge decks prone to vortex-induced vibrations[D]. University of Braunschweig Institute of Technology and the University of Florence, 2011.

[11] GAO G, ZHU L. Nonlinearity of mechanical damping and stiffness of a spring-suspended sectional model system for wind tunnel tests[J]. Journal of Sound and Vibration, 2015, 355: 369−391.

[12] 高广中, 朱乐东, 吴昊. 弹簧悬挂节段模型机械频率和阻尼的非线性特性识别[C]// 中国土木工程学会; 中国空气动力学会. 中国土木工程学会; 中国空气动力学会, 2013. GAO Guangzhong, ZHU Ledong, WU Hao. Identification of nonlinear structural damping and frequency for spring-suspended sectional model experiments[C]// The 16th National Conference on Structural Wind Engineering & The 2nd Forum on Wind Engineering for Graduate Students. Chengdu: 2013.

[13] Z Mingjie, X Fuyou. Nonlinear vibration characteristics of bridge deck section models in still air[J]. Journal of Bridge Engineering, 2018, 23(9): 04018059.1−04018059. 13.

[14] XU K, GE Y, ZHAO L. Quantitative evaluation of empirical models of vortex-induced vibration of bridge decks through sectional model wind tunnel testing[J]. Engineering Structures, 2020, 219: 110860.

[15] GAO G, ZHU L. Measurement and verification of unsteady galloping force on a rectangular 2:1 cylinder[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2016, 157: 76−94.

[16] 朱乐东, 庄万律, 高广中. 矩形断面非线性驰振自激力测量及间接验证中若干重要问题的讨论[J]. 实验流体力学, 2017, 31(3): 16−31. ZHU Ledong, ZHUANG Wanlü, GAO Guangzhong. Discussion several important issues in measurement and indirect verification of nonlinear galloping self-excited force on rectangular cylinders[J]. Journal of Experiments in Fluid Mechanics, 2017, 31(3): 16−31.

[17] GAO G, ZHU L, LI J, et al. A novel two-degree-of- freedom model of nonlinear self-excited force for coupled flutter instability of bridge decks[J]. Journal of Sound and Vibration, 2020, 480: 115406.

[18] Kareem A, Gurley K. Damping in structures: its evaluation and treatment of uncertainty[J]. Journal of Wind Engineering & Industrial Aerodynamics, 1996, 59(2/3): 131−157.

[19] GAO G, ZHU L. Nonlinearity of mechanical damping and stiffness of a spring-suspended sectional model system for wind tunnel tests[J]. Journal of Sound and Vibration, 2015, 355: 369−391.

[20] Ehsan F, Scanlan R H. Vortex-induced vibrations of flexible bridges[J]. Journal of Engineering Mechanics, 1990, 116(6): 1392−1411.

[21] 刘延柱, 陈立群. 非线性振动[M]. 北京: 高等教育出版社, 2001. LIU Yanzhu, CHEN Liqun. Nonlinear oscillations[M]. Beijing: Higher Education Press, 2001.

[22] ZHU L D, MENG X L, DU L Q, et al. A simplified nonlinear model of vertical vortex-induced force on box decks for predicting stable amplitudes of vortex-induced vibrations[J]. Engineering, 2017, 3(6): 779−914.

Influence of the nonlinearity of spring-suspended sectional model systems on Identification of vortex-induced vibration parameters

CHEN Zhengqing1, 2, XIAO Xiao1, 2, HUANG Zhiwen1, 2,HUA Xugang1,2

(1. Key Laboratory for Wind and Bridge Engineering of Hunan Province, Hunan University, Changsha 410082, China;2. Vibration and Shock Technology Research Center, Hunan University, Changsha 410082, China)

The influence of amplitude dependence of natural damping ratio of spring-suspended sectional model on identification of aerodynamic parameters of vortex-induced force was analyzed. Firstly, the expression of system’s equivalent damping ratio was given based on the principle of energy dissipation. Then, taking Scanlan’s nonlinear vortex-induced force model as an example, by solving the non-linear equation of motion, the response time history of the amplitude of the sectional model was obtained by solving the non-linear motion equation, and the identification method of the aerodynamic parameters considering the amplitude dependence of damping ratio was further explained. Then, considering the linear change of damping ratio of sectional model with amplitude, the parameters of a Rayleigh-Type nonlinear vortex-induced force model and Scanlan’s nonlinear model were identified respectively and compared. Finally, the influence of measurement error of damping ratio on identification results of nonlinear vortex-induced force was explained. The results show that the vibration amplitude of sectional model is affected by both aerodynamic parameters and nonlinear damping ratio of the system, and the identification of aerodynamic parameters can be identified by vibration testing. There are obvious differences between the Rayleigh-type model and the Scanlan’s model when the amplitude is stable, but these differences will not affect the prediction of the displacement response. Considering the amplitude dependence of the natural damping ratio of the structure, the influence of the identification error of the natural damping ratio on the identification results of the parameters of the vortex-induced force will be reduced accordingly.

vortex-induced vibration; parameter identification; bridge; sectional model; amplitude dependence

10.19713/j.cnki.43−1423/u. T20210090

TH212；TH213.3

A

1672 − 7029(2021)04 − 0821 − 09

2021−01−24

国家自然科学基金资助项目(51808210)

黄智文(1986−)，男，湖南怀化人，副教授，博士，从事大跨度桥梁抗风、结构振动控制的研究；E−mail：zwhuang213@hnu.edu.cn

(编辑 蒋学东)