基于Pumplinx的螺杆泵性能优化仿真研究

韩笑笑，苏 瑞，赵恒文，汪怡然，汪旭辉

（1.皖江工学院，安徽马鞍山 243031；2. 黄山工业泵制造有限公司，安徽黄山 245000）

0 引言

螺杆泵是一种旋转式容积泵，通过转子和定子啮合螺杆旋转增压输送介质，因其具有结构紧凑、输送平稳等优点被广泛应用于食品、石油、化工、环保等领域。常见的螺杆泵根据螺杆数量可以分为单螺杆泵、双螺杆泵和三螺杆泵等；根据螺杆泵转子和定子啮合时构成的螺旋腔是否密封，可分为密封型螺杆泵和非密封型螺杆泵，本文选择橡胶定子密封型单螺杆泵为研究对象［1-2］。

自1932年法国工程师MoiNeau发明单螺杆泵以来，人们一直致力于开发高效的单螺杆泵，对泵的水力性能进行了大量研究。姜东等［3］基于FLUENT软件对螺杆泵外特性数值模拟和试验进行了研究，分析了间隙，转速等参数对泵性能的影响。黄思等［4］基于Pumplinx软件对螺杆泵内非稳态流场特性及间隙泄漏规律进行研究，结果表明流量出现的脉冲次数与定子转子导程的比值一致。李倩等［5］通过数值计算与试验相结合的方法，对单螺杆泵的流场压力、流量波动、速度特性进行了分析，并基于仿真结果提出泵性能优化方案。刘增辉等［6］研究了材料磨损对单螺杆泵的性能影响，通过试验得出不同接触力和转速对材料的磨损率和磨损形式。NGUYEN等［7］提出了一种用于颗粒黏度估算的关联模型，通过建模方法研究了温度和压力对黏度的影响系数。MRINAL等［8］利用三维CFD制作模型的螺杆泵，来预测不同工况下的流动变量。前人对单螺杆泵的性能开展了大量研究，然而在螺杆泵结构参数上并没有进行深入研究，对不同参数条件下单螺杆泵的性能研究较少。

因此，本文引入无量纲参数T/D（定子导程T与转子直径D比值），基于Pumplinx软件，通过数值模拟研究了不同转速、压差、T/D比下单螺杆泵的的外特性与内部流动特性，得到了性能优化的T/D区间。

1 数值仿真方法

1.1 三维模型

本文模型泵选用橡胶定子单头单螺杆泵，三维模型如图1所示，其主要结构参数为：转子直径D为50 mm，转子偏心距e为9 mm，转子导程t为128 mm，定子导程T为256 mm，定子总长L为316 mm，转子与定子之间采用过盈配合，过盈量为0.6 mm。

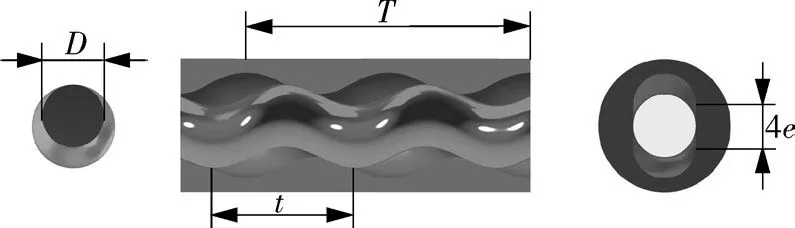
图1 单螺杆泵三维模型Fig.1 Three-dimensional model of single-screw pump

1.2 计算域与网格划分

本文假设定子、转子间存在连续间隙，与腔体共同组成连续水体作为数值计算域［9-12］。使用Pumplinx软件笛卡尔网格生成器对单螺杆泵流体计算区域进行结构网格划分。为了在节约计算时间的同时尽量保障计算精度，本文经过对模型泵的网格无关性验证（见表1），最终选择网格单元数为487 644的网格组3作为全文数值计算用网格，其定子、转子区域网格如图2所示。

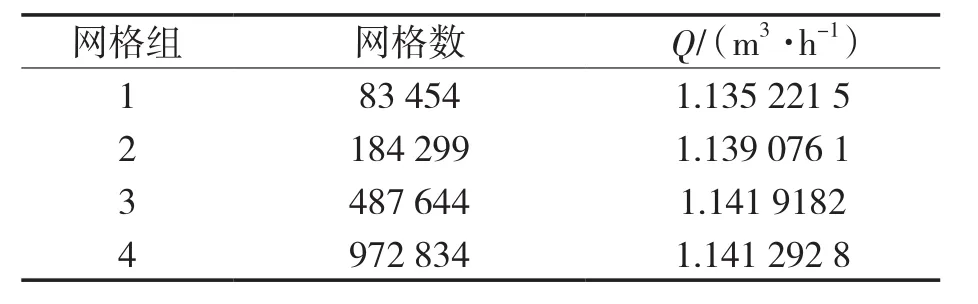
表1 网格无关性验证Tab.1 Grid independence verification

图2 网格无关性验证Fig.2 Grid independence verification

1.3 边界条件与求解方法

本文数值计算边界条件与模型泵试验条件相同，转速 n=200～500 r/min，压差 ΔP=0.2～0.6 MPa，介质为水，其密度为998 kg/m3，动力黏度为1.003 mPa·s。进口边界条件为压力进口，值为0.1 MPa，出口边界条件为压力出口，值为压差和进口压力之和；选取的Pumplinx计算模板包括：Progressive、Turbulence、Cavitation、Streamline；湍流模型为Standard k-ε模型，空化模型为Full Cavitation Model。求解器基于非定常数值计算进行设置，转子旋转一周为180个时间步长，即转子旋转2°为一个时间步长，时间步长为Δt=60/（180n）。选取转子旋转第5周的计算结果进行分析，求解器的残差达到Pumplinx软件瞬态计算默认的收敛标准，可保证足够的计算精度。

2 计算结果

2.1 模型泵非定常数值仿真结果

图 3（a）～（c）分别为压差 ΔP=0.2 MPa下泵旋转一周时域范围内流量Q，功率P，径向力Fx随时间t的变化曲线。由图可知，在一个旋转周期T（T=60/n）内，模型泵流量Q，轴功率P，轴向力Fx随时间呈周期性波动，周期数为2，与模型泵定子头数相同。则一个旋转周期内泵的时均流量为：

Qt—— 非定常计算每个时间步长的瞬时流量；

k —— 一个旋转周期内的时间步长，共计180个；

由非定常数值计算结果经时均流量计算公式可得，压差ΔP=0.2 MPa下的模型泵时均流量为1.35 kg/s；时均轴功率和轴向力可由相同方法计算得出。

图3（d）示出压差0.2 MPa下模型泵旋转一周轴向力Fy和Fz随时间变化的曲线。轴向力Fy和Fz在一个旋转周期内波动为1个周期，与转子头数相同。

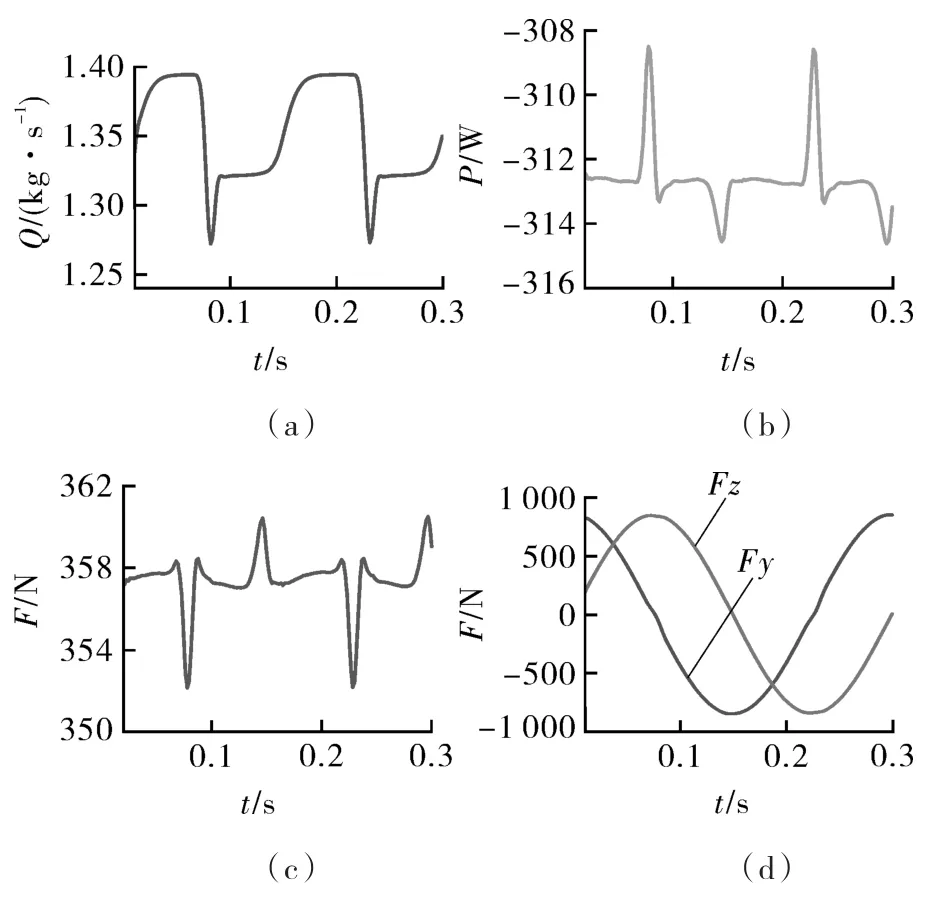
图3 螺杆泵外特性非定常数值计算结果Fig.3 Unsteady numerical computational results of external characteristics of the single-screw pump

2.2 模型泵外特性分析与试验对照

为探究在不同压差情况下时均流量Q和转速n之间的关系，开展了模型泵外特性试验，并将试验结果与数值计算结果进行对比。不同工况条件下流量的试验数据与仿真数据的对比如图4所示。从图中可以看出：相同压差条件下，泵流量和转速n呈线性正相关；相同转速条件下，泵流量随着压差ΔP的增大而减小。对比相同工况点的数据可以得出，仿真数据与试验数值的偏差基本维持在3%以内，最大偏差值为3.15%，出现在转速n为200 r/min的工况下。且随着转速n的增大，仿真偏差先减小后增大。

图4 试验数据与数值计算结果对比Fig.4 Comparison of test data and numerical computational results

2.3 不同T/D下单螺杆泵外特性

本文研究了转速n=200 r/min，进出口压差为0.05～0.04 MPa。由原型泵的T/D值为5.12，且导程T小于定子长度L，定义T/D取值范围为4～6。从图中可知，相同压差条件下，流量Q与T/D值成基本正比，近似为直线且不同压差条件下的斜率不同。由流量公式Q=4eDTn/60计算知，理论的直线斜率为0.3 kg/s，通过线性回归计算不同压差（由小到大的顺序）条件下斜率分别为0.278，0.268，0.258，0.251，0.224 kg/s。由此可知压差越小流量Q越趋近于理论值。

图5 不同压差条件下T/D-Q曲线Fig.5 T/D-Q curve diagram under different pressure difference conditions

螺杆泵水力效率计算式：

通过式（2）计算得到不同压差和T/D条件下的水力效率，结果如图6所示。从图中可以看出：相同T/D条件下水力效率随着压差的增大而减小；同时，在相同压差情况下随着T/D的增大，水力效率呈现先增大后减小的趋势，在4.5的时候可取到最大值，即T/D=4.5时该泵水力效率最高。初步判断该泵水力效率先增大后减小的原因是：在T/D＜4.5时，转子与定子的啮合区域面积较大，泵理论流量对该泵水力效率的影响较大，随着导程T的增大泵理论流量增大进而水力效率增大；在T/D＞4.5时，转子与定子的啮合区域面积较小，啮合区域的泄漏流对该泵水力效率的影响较大，随着导程T的增大定子转子啮合出泄漏量增大进而水力效率减小。

图6 不同压差条件下T/D-η曲线Fig.6 T/D-η curve diagram under different pressure difference conditions

在ΔP=0.2 MPa，不同T/D条件下螺杆泵的轴向力如图7所示。从图中可以看出，轴向力随着T/D的增大而略微增大，轴向力最大值与最小值的偏差不超过1%，即可认为T/D对螺杆泵轴向力的大小基本无影响。

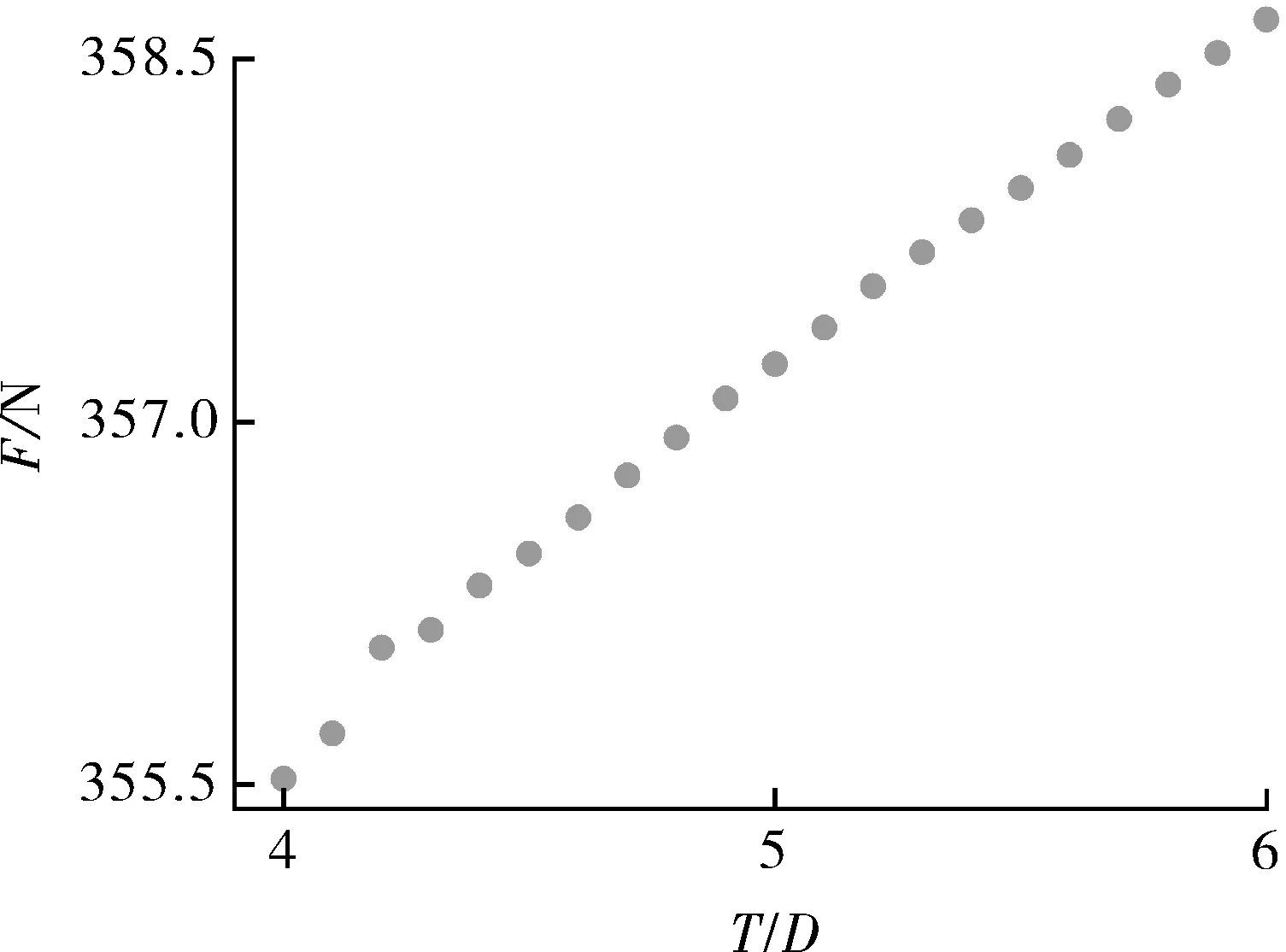
图7 0.2 MPa压差条件下T/D-Fx曲线Fig.7 T/D-Fx curve diagram under 0.2 MPa differential pressure

基于螺杆泵外特性数值计算结果对比，在相同压差条件下为了得到更高的水力效率，螺杆泵T/D应优化至4.5最为合适；为了得到更大的流量，在效率偏差不超过1%的前提下，螺杆泵T/D应优化至5.4最为合适。

2.4 流场分布规律

T/D=4.0，4.5，6.0 时，n=200 r/min，ΔP=0.2 MPa条件下，z=0截面上流体域的流速矢量及定子转子表面静压分布如图8所示。

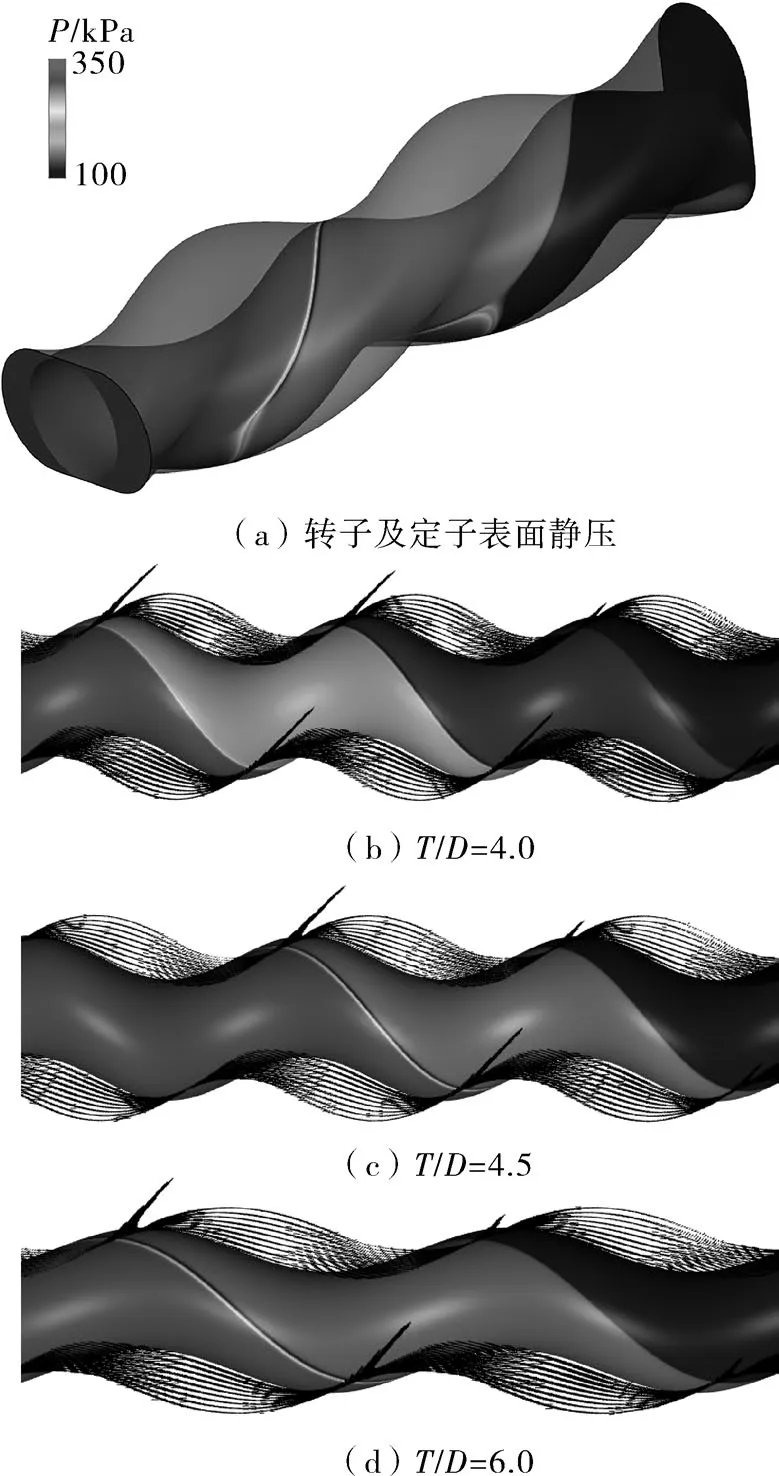
图8 螺杆泵速度矢量及压力分布Fig.8 Speed vector and pressure distribution diagram of the screw pump

从图8（a）可见，由进口段至出口段压力在各腔室呈阶梯式增大，每个腔内压力值基本相等。从图8（b）～（d）可见，相邻腔室内高压腔的流体沿定转子啮合线向低压腔回流，即螺杆泵出现泄漏。在相同T/D的条件下，高压差的腔室间泄漏流速比低压差的泄漏流速快。对比不同T/D的流速矢量图可知，T/D=6.0时螺杆泵的泄漏量高于T/D为4.0，4.5时。T/D为4.5，4.0时的泄漏情况近似，其中4.0略优于4.5。螺杆泵泄漏情况会严重影响泵的水力效率，这与外特性分析水力效率的变化规律基本一致。

3 结论

（1）在相同压差条件下，随着T/D的增大，螺杆泵流量增大，轴向力不变，水力效率先增大后减小，定子转子啮合区域泄露量明显增大。

（2）基于数值计算结果分析，为了得到更高的水力效率，螺杆泵T/D应优化至4.5最为合适；为了得到更大的流量，在效率偏差不超过1%的前提下，螺杆泵T/D应优化至5.4最为合适。