径向流体支点可倾瓦轴承润滑特性分析
王晓红,常山,裴世源
(1.中国船舶集团有限公司第703研究所,150036,哈尔滨; 2.西安交通大学现代设计及转子轴承系统教育部重点实验室,710049,西安)
机械装备日渐向高速重载方向发展,径向可倾瓦轴承以其承载力大、稳定性高等优点成为大型关键装备首选的支撑方案,并在工程中大量应用。然而,传统可倾瓦轴承存在以下劣势或缺点:①支点磨损,支点通常采用点或线接触,在高速重载工况下,很容易产生瓦块变形、磨损等故障,导致轴承工作状态恶化;②轴承体积大,所需的安装空间大;③轴承阻尼小,虽然其自身不会引起半频涡动,但其抵抗气隙激励和油封激励的能力亦有不足;④存在累积误差,轴承间隙和预负荷受支点、瓦块、基座、轴颈四者加工精度的影响,对加工和装配要求高。
为克服传统可倾瓦轴承的缺点,近年来,流体支点可倾瓦轴承以其阻尼大、体积小、无磨损等特点受到广泛重视,并在高速压缩机、燃气轮机中大量应用。1977年Hollingsworth提出了流体支点可倾瓦轴承的概念,详细地描述了轴承的工作机理,并讨论了轴承的优点与轴瓦的浮动状态[1]。Harangozo等提出直接通过轴承壳上的孔向衬垫供油的设计构想,提高了轴承的承载能力,降低了轴承的功率损耗[2-4]。Messmer优化了流体支点可倾瓦轴承轴瓦的表面形状,使转子系统在受到冲击、振动、不均匀载荷等时,仍有良好的减振性能[5]。Desbordes等对轴瓦的形状和位置的进一步优化,利用分布在轴瓦两表面流体动、静压油膜的反馈特性,使转子系统的机械变形和热变形显著降低[6]。Shin等对比分析了流体支点可倾瓦轴承与普通轴承性能差异,结果表明在一定工况条件范围内流体支点可倾瓦轴承显著改善了转子系统的动态性能[7]。Hemmatian等使用电涡流探头监测了不同工况下轴瓦的浮动状态变化,观察到轴瓦在一定转速和负载范围内可能处于单侧浮动状态或完全浮动状态,并发现轴承在两种状态下的性能差异较大[8-9]。Haugaard和Santos在研究流体支点轴承的润滑特性时考虑了瓦块的柔性变形,并对瓦块的倾斜角度进行了数值模拟[10-11]。Deckler等对流体支点可倾瓦轴承的动态油膜反馈机制进行了监测,实现了轴瓦两侧油膜的动态调节,并且采用试验的方法验证了理论模型的正确性[12-14]。Mikula等分析了瓦块开口槽位置对轴承支撑性能的影响,研究表明开口槽的位置和大小会显著影响轴承的温升[15-17]。杨期江等研究了柔性阻尼可倾瓦轴承的减振特性,阐述了流体支点可倾瓦轴承油膜的形成机理,通过相似性原理搭建了倒置式试验台并验证了轴承的动力学特性[18-20]。罗健彬开发了一款变支点可倾瓦轴承的测控系统,通过在线数据采集系统对轴承进行了一系列的试验,验证了该轴承的可行性[21-22]。Lou等通过理论和试验研究了半浮动状态下轴承的润滑性能[23-24]。
虽然流体支点可倾瓦轴承已经具有40多年的历史,但由于它的工作机理、润滑特性、轴瓦浮动状态等均较为复杂,导致其理论研究进展远落后于试验研究和工程应用。现有文献主要集中在流体支点可倾瓦轴承的发展史、工作原理、试验研究以及定性描述轴承的减振性能等方面,对于流体支点可倾瓦轴承的设计、润滑性能、瓦块浮动过程等方面的研究鲜有报道。本文针对流体支点可倾瓦轴承瓦块空间状态不确定性高、多场耦合非线性强、整体自由度多等分析难点,结合流体支点可倾瓦轴承运转及轴瓦浮动状态的变化过程建立了理论分析模型,采用有限元分析方法联立求解了能量方程、雷诺方程、温黏方程等,得到了流体支点可倾瓦轴承的静动特性,对比了典型工况下流体支点可倾瓦轴承与传统固定瓦轴承、机械支点可倾瓦轴承的性能差异,分析了3种轴承的性能参数随转速、载荷的演化规律,最后基于理论分析结果探讨了瓦块的不稳定现象。
1 理论方法
1.1 工作机理
流体支点可倾瓦轴承工作原理如图1所示,在轴瓦内侧与轴颈之间会形成动压油膜,与此同时润滑油通过轴瓦中央的小孔进入到轴瓦外侧与轴承壳体形成的空腔中,并在轴瓦外表面与轴承壳体之间形成静压油膜。由于轴颈和轴瓦内侧的动压效应以及瓦块中央的小孔,轴瓦两侧的动压和静压会相互平衡,使轴瓦处于浮动状态。若轴承的几何参数或运行参数改变,瓦块的浮动状态与倾斜角度也会发生变化,但是轴瓦会在动压油膜和静压油膜的动态反馈中重新达到平衡状态。

图1 流体支点可倾瓦轴承工作原理[24]Fig.1 Working principle of fluid pivot tilting pad bearing
流体支点可倾瓦轴承的轴瓦在工作过程中可能存在完全接触、完全浮动、单边浮动3种不同的浮动状态,如图2所示。对于完全接触状态,此时轴瓦无法转动,轴承相当于固定瓦轴承;对于完全浮动状态,此时轴承动静特性比较复杂,需要通过迭代计算确定平衡位置;对于单边浮动状态,此时要重新建立力矩平衡来求解轴承的动静特性参数。
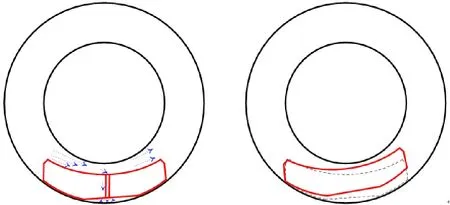
(a)完全接触 (b)单边浮动

(c)完全浮动 (d)整体自由度多图2 流体支点可倾瓦轴承的浮动状态Fig.2 Floating state of fluid pivot tilting pad bearing
流体支点可倾瓦轴承在正常工况下运行时,轴瓦由于静压油膜压力和动压油膜压力相互作用而处于平衡状态。当轴承的运行参数改变时,若形成的静压油膜压力大于动压油膜压力,则轴瓦的浮动量增大,此时动压效应增强从而使动压油膜压力增大,进而使轴瓦两侧油膜压力重新达到平衡;若形成的静压油膜压力小于动压油膜压力,则轴瓦的浮动量减小,此时轴瓦可能保持在完全接触状态或单边浮动状态,但是由于轴瓦浮动量减小,最小油膜厚度增大,动压油膜的压力显著降低,静压油膜压力虽然也会降低,但其与动压油膜压力的差值逐渐减小,使得轴瓦两侧的油膜压力重新达到平衡。
1.2 控制方程
径向流体支点可倾瓦轴承的计算方法和数值方法参考文献[24],其中稳态、不可压缩条件下,内外层油膜的流动状态均可以用如下雷诺方程进行描述[25]
(1)
式中:x=Rθ,U=Rω,Re=ρUh/μ,Re为雷诺数;μ为润滑介质黏度;p为油膜压力;h为油膜厚度;ρ为润滑油密度;Q为静压孔处的流量,对于内外层油膜其值相等,符号相反,内层动压油膜为负,外层静压油膜为正;Gx和Gy分别是x方向和y方向的紊流修正因子,其表达式如下式
(2)
(3)
能量方程[25]为
(4)
1.3 轴承静特性
根据流体支点可倾瓦轴承的结构特点,轴承的油膜合力为
(5)

摩擦阻力为
(6)
功耗为
P=FtRω
(7)
动压油膜中通过轴瓦中央小孔进入到静压腔中的流量为
(8)
动特性中刚度、阻尼系数的计算参照文献[26-27]中所给出的方法进行,因公式表达较为烦琐,限于篇幅此处不再逐项给出。
1.4 边界条件
对于雷诺方程,瓦块上下游的压力设定为供油压力,瓦块两侧的压力设置为0,分别由下式确定
p|y=0=p|y=L=ps
(9)
p|ζ=±B/2=0
(10)
对于油膜空化现象,本文采用JFO质量守恒边界处理油膜破裂和再形成边界,由下式确定
(11)
(12)
需要注意的是采用JFO质量守恒边界需要同时求解压力场、密度场和黏度场,密度场和黏度场满足下式的关系
(13)
(14)
式中:r为油膜占空比。轴瓦在平衡状态下,动压腔流入静压腔的流量与静压腔流出的流量相等,轴瓦内外表面所受的力和力矩相等,动压和静压油膜两端出油口压力均为大气压,且出口厚度方向的压力梯度为0。关于流体支点详细边界的讨论可参见文献[23]。
1.5 数值计算
本文采用有限元方法对雷诺方程和能量方程进行求解,采用9节点二阶等参元对雷诺方程进行离散,其相对于4节点双线性等参元在流量计算方面具有更高精度。使用高斯积分计算油膜合力,摩擦力、流量等静特性参数。采用Newton-Raphson算法迭代求解轴颈水平和竖直方向上的偏心距、油膜温度和油膜占空比,迭代精度为10-3,最终压力场、温度场及油膜占空比均达到收敛后,采用小扰动法求解动特性系数[26-27]。图3给出了流体支点可倾瓦轴承稳态计算程序的流程图。
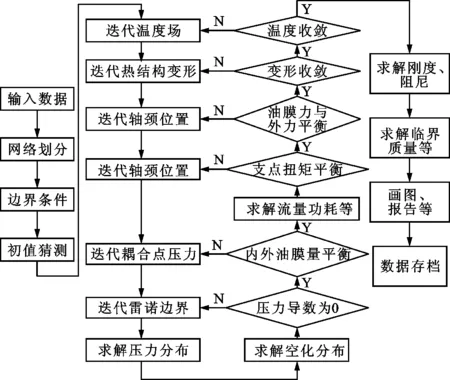
图3 流体支点可倾瓦轴承稳态计算程序流程图Fig.3 Flow chart of the proposed model
2 结果与讨论
2.1 算例描述
为对比研究流体支点可倾瓦轴承与传统固定瓦轴承、机械支点可倾瓦轴承的性能差异,本文分析了3种轴承在典型工况下的润滑特性以及轴承性能参数随转速、载荷的变化规律。固定瓦轴承、机械支点可倾瓦轴承、流体支点可倾瓦轴承的主要几何参数与工况条件如表1所示。

表1 典型工况下轴承主要几何参数与工况条件
2.2 典型工况下3种轴承润滑特性对比

图4 固定瓦轴承油膜压力分布图Fig.4 Film pressure distribution of fixed pad bearing
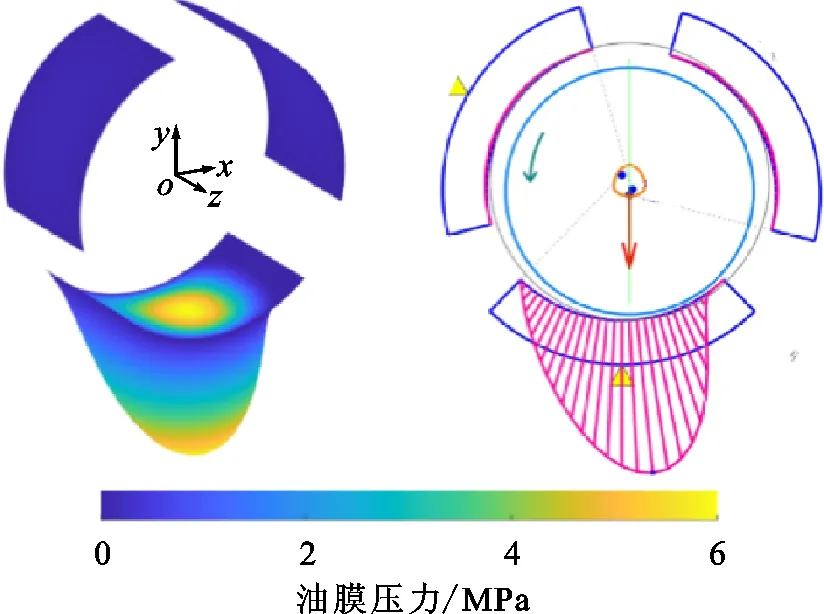
图5 机械支点可倾瓦轴承油膜压力分布图Fig.5 Film pressure distribution of mechanical pivot tilting pad bearing

图6 流体支点可倾瓦轴承油膜压力分布图Fig.6 Film pressure distribution of fluid pivot tilting pad bearing
在典型工况下,3种轴承的油膜压力分布如图4~6所示,部分静动特性参数如表2所示,根据表2可得:同工况条件下,流体支点可倾瓦轴承的最小油膜厚度最大,最大油膜压力最小,油膜温升最低,刚度和阻尼值显著大于另外两种轴承,即流体支点可倾瓦轴承具有较好的安全性和稳定性。相比之下流体支点可倾瓦轴承也有缺点,其功耗比固定瓦轴承和机械支点可倾瓦轴承均有增加。原因在于流体支点可倾瓦轴承具有双层油膜,油膜总体厚度远大于传统轴承,因此轴承运行需要更大的流量,流量增加的同时降低了轴承的温度,从而使轴承的功耗增大。但相比于流体支点可倾瓦轴承在性能方面的显著提升,流量提升带来的功耗增加是可以接受的。

表2 3种轴承静动特性参数对比
2.3 3种轴承静动特性随转速的变化
本节采用Newton-Raphson迭代法联立求解雷诺方程、温黏方程等,计算了转速为1 000~5 000 r·min-1范围内固定瓦轴承、机械支点可倾瓦轴承、流体支点可倾瓦轴承的油膜厚度、油膜压力和直接刚度、阻尼,分析了3种轴承润滑特性随转速的变化,结果如图7~10所示。
根据图7可得,固定瓦、机械支点、流体支点3种轴承的最小油膜厚度都随着转速的增大而增大,且变化趋势逐渐变缓。在相同转速下,流体支点可倾瓦轴承的最小油膜厚度最大,机械支点轴承最大油膜厚度次之,固定瓦轴承的最大油膜厚度最小。这是因为流体支点可倾瓦轴承在工作过程中瓦块出油边单边浮动,此时轴承的实际性能变化与增加偏支系数一致,延后了油膜的破裂角度,增加了瓦块的有效承载面积(由图5和图6对比可得),故最小膜厚有所增加。

图7 最小油膜厚度随转速的变化 Fig.7 Variation of minimum oil film thickness with rotating speed
根据图8可知,3种轴承随着转速的增大,切向速度增加,动压效应增强,最大油膜压力缓慢减小。在相同转速下,流体支点轴承的最大油膜压力最小,固定瓦轴承的最大油膜压力次之,机械支点轴承的最大油膜压力最大,即相同负载下流体支点可倾瓦轴承具有最小的油膜压力。
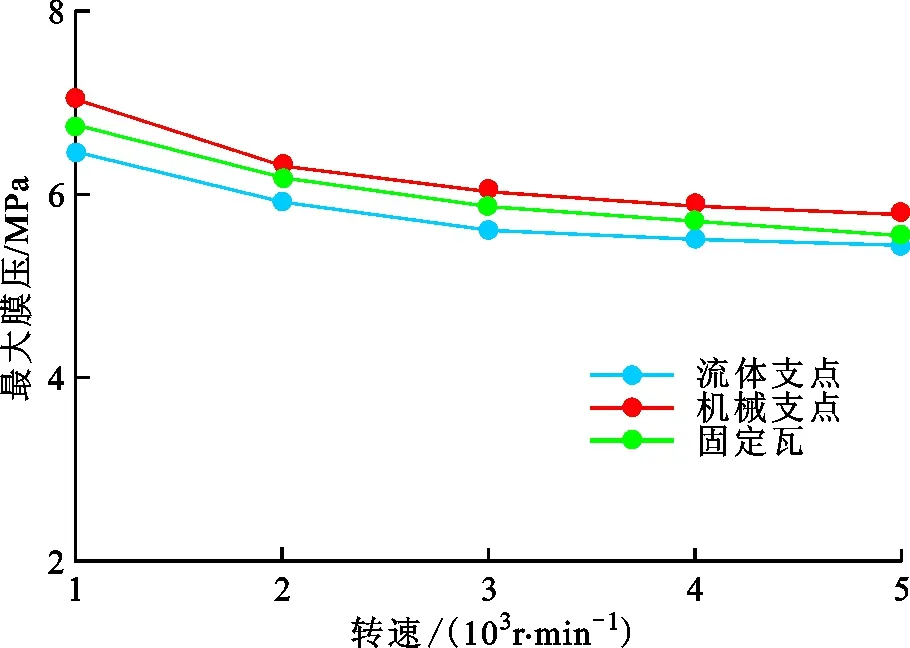
图8 最大油膜压力随转速的变化 Fig.8 Variation of maximum oil film pressure with rotating speed
根据图9可得,转速对3种轴承的刚度影响较小,同转速下流体支点可倾瓦轴承的直接刚度远大于其他两种轴承,其值约为其他轴承的6倍,即流体支点可倾瓦具有较高的稳定性。

图9 kyy随转速的变化Fig.9 Variation of kyy with rotating speed
根据图10可得,流体支点可倾瓦轴承的直接阻尼显著高于其他两种轴承,其值随着转速的增大而先减小后增大,且变化趋势复杂,与其瓦块的浮动状态有关。而机械支点轴承和固定瓦轴承的直接阻尼低于流体支点可倾瓦轴承1~2个数量级。3种轴承在相同转速下,流体支点轴承的直接阻尼最大,具有较好的阻尼特性,转子系统的稳定性显著增加。
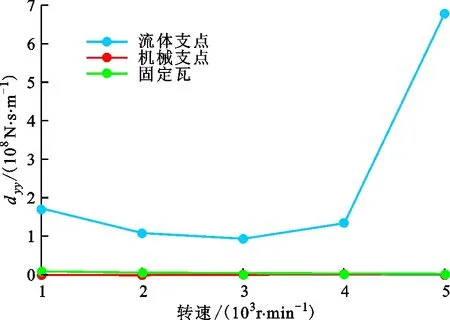
图10 dyy随转速的变化Fig.10 Variation of dyy with rotating speed
2.4 载荷的影响
本节采用Newton-Raphson迭代法联立求解雷诺方程、温黏方程等,计算了载荷在3~15 kN范围内固定瓦轴承、机械支点可倾瓦轴承、流体支点可倾瓦轴承的油膜厚度、油膜压力和直接刚度、阻尼,分析了3种轴承润滑特性随载荷的变化,如图11~14所示。
根据图11可得,载荷在3~15 kN范围内,固定瓦、机械支点、流体支点3种轴承的最小油膜厚度都随着载荷的增大而减小,且变化趋势逐渐变缓。相同载荷下,机械支点轴承的最大油膜厚度与固定瓦轴承的最大油膜厚度相近,流体支点轴承的最小油膜厚度最大。

图11 最下油膜厚度随载荷的变化Fig.11 Comparison of minimum oil film thickness with load
根据图12可得,载荷在3~15 kN范围内,固定瓦、机械支点、流体支点3种轴承的最大油膜压力都随着载荷的增大而增大,且变化趋势呈线性,低载荷下3种轴承差异不明显,当载荷增大至1 kN以上时,流体支点可倾瓦轴承的油膜压力明显较低。

图12 最大油膜压力随载荷的变化Fig.12 Variation of maximum oil film pressure with load

图13 kyy随载荷的变化Fig.13 Variation of kyy with load
根据图13可得,载荷在3~15 kN范围内,3种轴承的直接刚度随载荷的增大而增大,但是流体支点轴承刚度随载荷的变化趋势比其他两种轴承大。同载荷下,流体支点轴承的直接刚度最大,机械支点和固定瓦轴承直接刚度比较接近。
根据图14可得,载荷在3~15 kN范围内,流体支点可倾瓦轴承的直接阻尼远高于固定瓦轴承和机械支点轴承,即转子系统的稳定性有望得到显著增加。值得注意的是,在6 kN载荷下,流体支点可倾瓦轴承的直接阻尼发生了突跳,而本文仔细校验了该工况下轴承的润滑状态,发现可能是由于瓦块的不稳定现象所引发的,并在下节详细讨论。
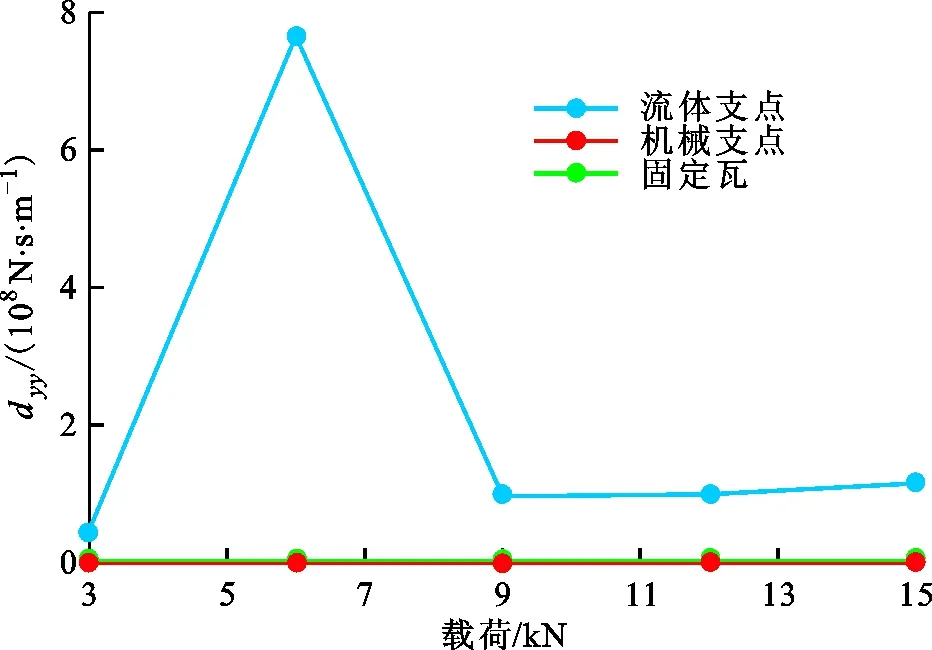
图14 dyy随载荷的变化Fig.14 Variation of dyy with load
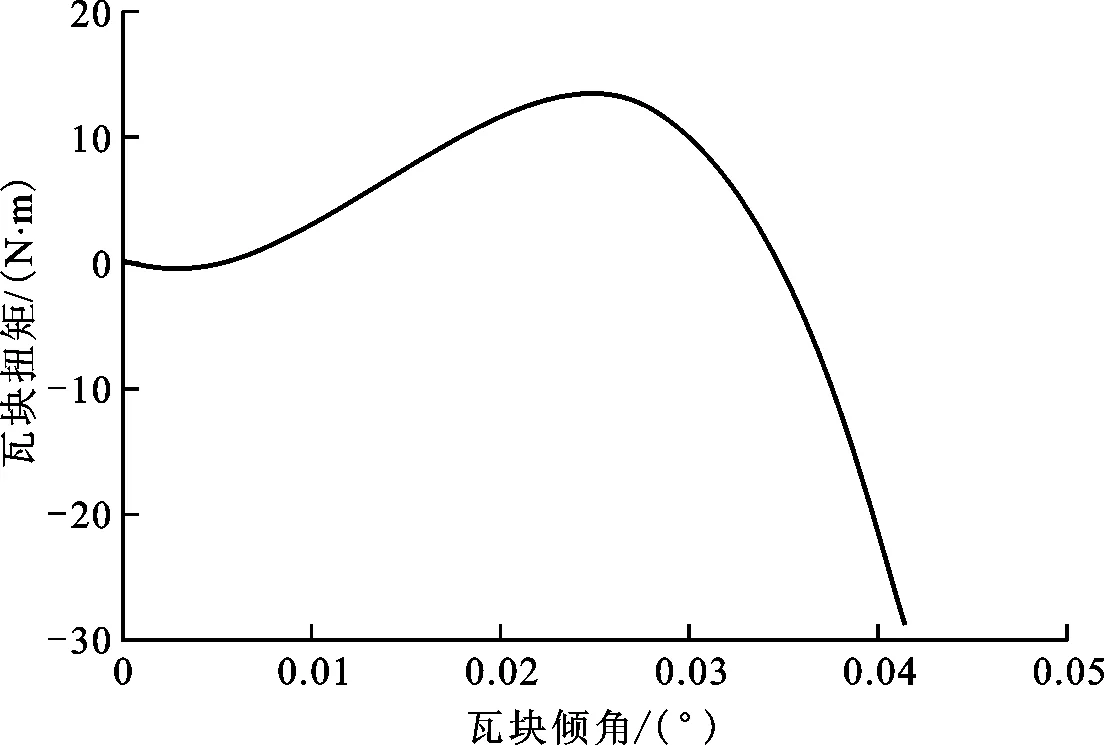
图15 轴承瓦块扭矩随瓦块倾角的变化Fig.15 Effect of pad inclination angle on pad torque
2.5 瓦块的不稳定现象
图15为轴承瓦块扭矩随瓦块倾角的变化曲线。根据图15中变化曲线可得,随着轴承瓦块倾角增加,瓦块自身扭矩呈现先上升后下降的趋势。只有当扭矩为0时,瓦块才能达到稳定状态,当扭矩不为0时,瓦块会根据扭矩的正负产生相应方向的转动,使轴承重新达到平衡状态。当瓦块倾角为0.004°和0.35°时,瓦块扭矩均为0,即表明流体支点可倾瓦轴承轴瓦存在两个稳定点。当轴承受到外界干扰(冲击、振动、不均匀载荷等)时,瓦块极有可能在两个稳定状态点之间发生跳跃,进而导致轴承瓦块存在不稳定现象,从而影响转子系统的稳定性。
图16为瓦块倾角变化过程中轴瓦两侧动压和静压油膜压力的分布。根据图16可得,当瓦块倾角在0°~0.01°和0.03°~0.04°之间变化时,瓦块两侧油膜压力分布发生突变。结合图15~16可得,当瓦块倾角在两个平衡位置之间变化时,瓦块内外层油膜压力分布具有明显差异,这就意味着此时瓦块状态发生了突变,即验证了瓦块的不稳定现象。但本文仅从理论的角度给出了流体支点可倾瓦轴承的不稳定现象,还需要通过实际测试辅以验证。
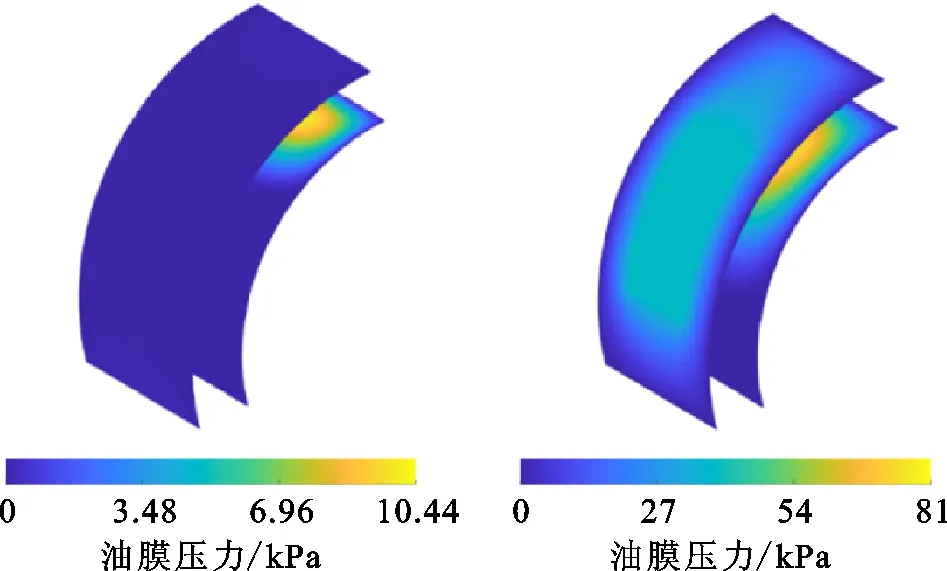
(a)0° (b)0.01°

(c)0.03° (d)0.04°图16 不同瓦块倾角下油膜压力的分布 Fig.16 Film pressure distributions under different pad inclination angles
3 结 论
本文研究流体支点可倾瓦轴承不同工况条件下的润滑性能,同时对比了其与传统固定瓦和可倾瓦轴承静动特性参数,得到以下结论:
(1)流体支点可倾瓦轴承结构紧凑、体积小、无支点磨损问题、阻尼大。采用内外油膜互通的供给静压方式,不仅省去了复杂的密封结构,同时利用了动静压的反馈机制,实现了油膜的动态调节,显著提升了轴承的安全性与转子系统的稳定性。
(2)对于本文所研究的工况,流体支点可倾瓦轴承在工作过程中瓦块出油边单边浮动,此时轴承的实际性能变化与增加偏支系数一致,延后了油膜的破裂角度,增加了瓦块的承载面积,相对于传统中心支撑机械支点可倾瓦或固定瓦轴承其最小膜厚更高,膜压和膜温更低,但其流量和功耗也更高,综合来说,流体支点可倾瓦轴承的静态性能优于传统固定瓦轴承和机械支点可倾瓦轴承。
(3)对于本文所研究的工况,相比于传统的固定瓦轴承和机械支点可倾瓦轴承,流体支点可倾瓦轴承的有效刚度和阻尼高约一个数量级,这是由于轴承内外层油膜自身的结构性质决定的。
(4)在某些工况条件下,流体支点可倾瓦轴承瓦块存在两个稳定平衡点,当轴承受到外界干扰(冲击、振动、不均匀载荷等)时,瓦块有可能在两个稳定平衡点之间发生跳跃,进而导致轴承瓦块存在不稳定现象,但本文仅从理论的角度给出了流体支点可倾瓦轴承的不稳定现象,还需要通过实际测试辅以验证。

