基于风险分析的导流方案比选在某水利枢纽工程中的应用

余建平，肖 钰，徐轶慷，吴留伟

（浙江省水利水电勘测设计院，浙江 杭州 310002）

1 问题的提出

水利枢纽工程中施工导流方案是施工总体方案中的关键组成部分，与枢纽布局、大坝坝型、施工筹划、施工度汛、大坝蓄水等问题紧密相关。导流方案的选定，关系到整个枢纽工程施工安全、施工工期、施工质量、工程造价及度汛安全等，因此需进行多方案的比较、论证，并根据实际情况辅以必要的模拟研究，才能优选出合理可行的方案。

从目前趋势来看，包含导流风险分析的多目标决策将在今后导流方案选择上得到更多推广应用。SL 303—2017《水利水电工程施工组织设计规范》中指出，可对大中型或有特殊要求的水利水电工程进行风险度分析，因此对导流风险分析和导流方案多目标决策模型进行研究应用非常必要。本文结合浙南某水利枢纽工程，在导流风险分析的基础上，对影响导流方案选择的主要目标进行量化和综合分析，运用多目标决策模型对导流方案进行优选，为今后类似设计工作中导流方案的选择提供参考依据和思路。

2 工程概况

工程位于浙南，集水面积311.9 km2，水库总库容3.63亿m3，工程等别为Ⅱ等，规模为大（2）型，主要建筑物拦河坝为1 级。建筑物主要有拦河坝、泄水建筑物、放水建筑物等。拦河坝设计为抛物线型双曲变厚混凝土拱坝，坝顶高程181.00 m，最大坝高126.00 m。导流建筑物为4级，初期导流采用断流围堰、左岸隧洞导流、基坑梅汛期施工的导流方案，中后期导流采用坝上开设导流底孔联合导流隧洞泄流、度汛的方案。导流平面布置见图1。

图1 导流平面布置图

初期导流建筑物包括导流洞与上下游围堰，中后期导流建筑物包括导流洞以及坝上开设的导流底孔。初期左岸导流洞进口底板高程为76.00 m，出口底板高程为74.00 m，洞身开挖断面初拟为9.00 m×9.00 m，衬后为8.00 m×8.00 m的城门洞型。上游围堰采用土石过水型式，设计挡水流量889 m3/s，堰顶高程93.60 m，最大堰高17.60 m，堰体上游坡为1:1.5，下游边坡为1:3.0；下游围堰采用土石过水型式，最大堰高3.30 m。导流底孔设置高程为77.00 m，孔口尺寸为2 孔5.00 m×5.00 m（宽度×高度）。

3 施工导流风险分析

国内外不少学者在施工导流风险分析方面做了很多探讨，提出一些导流风险模型[1]。近来又有学者提出利用Monte-Carlo 方法，通过统计分析模型确定动态风险[2]。但是在模拟施工洪水过程中，只考虑了洪峰流量的不确定性，而没有洪水过程洪量和历时不确定性，以及导流建筑物各种水力参数的不确定性[3]。为此，本文将多重不确定性因素引入导流风险计算模型中，即具体分析和确定影响水文、水力和库容等多重不确定性因素的随机分布，并考虑随机因素，再通过计算机ⅤB 语言编程运用Monte-Carlo 方法来模拟施工洪水过程和泄流能力等，然后通过导流风险计算模型得到导流风险度。

3.1 施工导流风险计算模型

本工程导流风险分析在于确定围堰上游水位风险，即系统考虑河道来流、导流建筑物泄流以及枢纽的其他特征，通过系统模拟的方法来实现。其步骤为[4]：

（1）收集相关资料，包括水位库容关系曲线，典型洪水过程线，坝址处水文资料、枢纽布置及其参数等，计算泄水建筑物下泄能力。

（2）抽样[0，1]区间的伪随机数。

（3）根据坝址处的水文资料，得到围堰挡水期内的流量均值、偏态系数、偏差系数。根据公式计算洪水过程曲线P-ⅠⅠⅠ的洪峰随机变量。

（4）合理确定正态分布的方差、三角分布的下限值、均值、上限值，根据下列公式计算正态分布和三角分布的随机变量，抽样值分别乘以相应的库容和下泄流量，得到一组随机水位库容关系曲线和随机下泄能力曲线。

正态分布：采用乘分布的舍选抽样，ƒ(x)=H(x)ƒ1(x)，取ƒ1(x)=exp(-｜x｜)/2；三角分布：分布密度函数为

式中：a、b、c为分布密度函数区间取值。

（5）依据随机洪水过程、随机水位库容曲线和随机下泄能力曲线对围堰上游水库进行调洪演算，得到围堰上游水位。

（6）统计围堰上游水位超过围堰顶高程的次数，其与总抽样次数的比值即为围堰挡水风险。

3.2 施工导流风险计算参数

3.2.1 坝址水位库容关系

坝址处的水位与库容关系见图2。

图2 坝址水位与库容关系曲线图

3.2.2 设计洪水过程

导流设计中使用的设计洪水过程，非汛期（10，20，50，100 a 一遇）见图3；梅汛期（10，20，50，100 a 一遇）见图4；台汛期（10，20，50，100 a 一遇）见图5。

图3 非汛期设计洪水过程线图

图4 梅汛期设计洪水过程线图

图5 台汛期设计洪水过程线图

3.2.3 泄流能力计算

泄流能力分别按照明流过流、半有压流及有压流计算，计算成果见图6。

泄流能力受多种因素影响，根据施工导流风险分析和大量水电站设计的工程实践和运行观测分析，导流洞泄流能力变化的取值范围f=（0.97～1.05）Q。导流计算认为导流洞泄流能力服从三角形分布[4]。

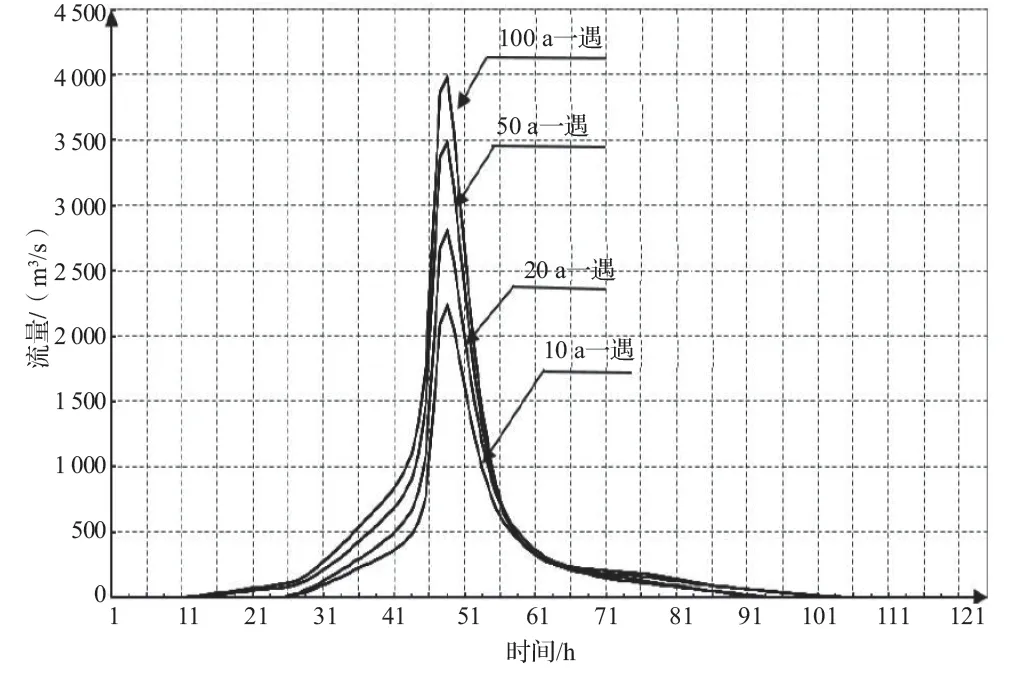
图6 泄流能力曲线图

3.2.4 设计洪水资料

依据坝址处的水文统计资料，得到坝址处各分期洪水流量均值，变差系数Cv值和偏态系数Cs值，以及各频率流量（见表1）。

表1 坝址处洪水成果表

3.2.5 各随机因素的统计性质及分布

各随机因素的统计性质及分布见表2。

表2 随机因素统计性质及分布表

3.3 施工导流风险计算成果

依据上述资料中的洪水统计参数，使用随机模拟抽样，同倍比法放大典型洪水过程线，结合随机抽样得到的水位库容关系曲线和隧洞泄流能力曲线，进行围堰堰前水位的调洪计算，得到各个抽样流量下的上游水位值，统计分析其超过上游围堰顶高程的样本数，进而得到围堰的挡水风险。

综合考虑水文随机因素、水力随机因素以及库容随机性，得到各分期设计标准洪水导流风险计算成果（见表3）。对于梅汛期10 a，20 a 一遇导流标准，各尺寸下的导流洞的设计水位均较高，且对应的导流风险率均高于设计洪水标准的风险率。

表3 导流风险分析计算成果表

续表3

4 导流方案比选

4.1 导流方案影响因素分析

在进行本工程导流方案选择时，需要在决策者能够接受的风险范围内综合确定性投资、导流围堰施工进度、超载洪水发生的导流建筑物损失及工期损失等指标进行综合评判并综合排序。

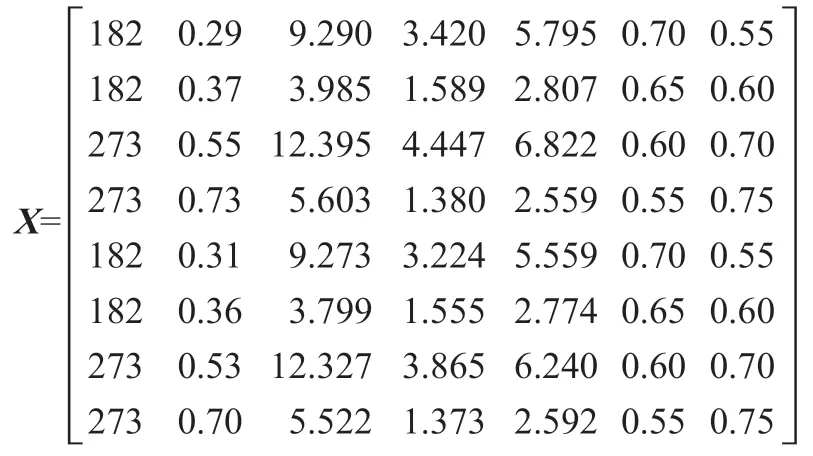
对导流方案（8 个）进行比较，具体见表4。

表4 导流方案参数比较表

4.2 导流方案比选计算方法

本工程导流方案的选择，可根据多目标风险决策模型运用熵权理论，把熵权和主观权重结合作为决策评价指标的综合权重。在分析和确定导流标准多目标决策主要指标的基础上，运用TOPSⅠS 多目标决策理论，依据最大隶属度原则，选择施工导流方案[4]。

设由n个指标来评价m个可行的施工导流方案，设第i个施工导流方案的第j个指标的特征值为aij，则对于所有可行的施工导流方案，其评价指标特征矩阵：

标准化处理后的隶属度矩阵R为：

4.2.1 主观权重计算

（1）对判断矩阵的每一行求和，即：

（2）对求和向量B=(b1,b2,...bn)T进行正规化，即：

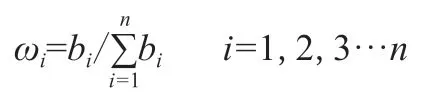
（3）主观权重向量ω为：ω=(ω1,ω2,...ωn)T且

4.2.2 综合权重计算

综合权重λ=(λ1,λ2,λ3,...λm)：

4.2.3 熵权计算

设第j项评价指标的熵值Hj为：

设第j项评价指标的熵权w0j为：

4.2.4 基于熵权的导流方案多目标决策模型

令特征向量Ri为：Ri=(ri1，ri2，…，rin)称ξ为 矩 阵R的正理想隶属度特征向量。称ζ为 矩 阵R的负理想隶属度特征向量。

施工导流方案i的正理想距离和负理想距离分别为L+(Ri,ξ)，L-(Ri,ζ)：

对于施工导流方案i，μi(vi)为从属于正(负)理想隶属特征向量的隶属度，则：

S+(Ri,ξ)，S-(Ri,ζ)为导流方案i的正理想度和负理想度。

为求得最优解，计算评价向量M和N可按最小二乘法优选准则，对所有导流方案，使S+(Ri,ξ)，S-(Ri,ζ)的广义距离平方和最小。根据这一优选准则建立目标函数：

4.3 导流方案比选计算成果

8 个导流方案的8 个属性形成的决策矩阵为：

各指标的熵权：

主观权重：

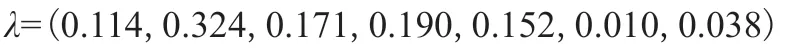
故加权规范矩阵：

正理想解：

负理想解：

贴近度集合：

由贴近度可以得到C3=0.850 是贴近度中最接近正理想解的。即方案3，梅汛期10 a 一遇挡水标准、导流洞洞径8.00 m×8.00 m 的方案为最佳导流方案。

5 结 语

在整个工程建设中，施工导流方案的选取对工程建设费用、工期及其可靠性等产生极大的影响。本文通过对浙南山区某水利枢纽工程导流风险计算，并在综合考虑8 个不同导流方案的挡水时间、导流建筑物投资、挡水风险、工期损失期望、投资损失期望、导流建筑物施工难度和大坝施工难度7 个决策指标的情况下进行方案比选。比选中非确定性指标采用熵权的模糊化处理，为导流方案的优选提供较为全面的决策信息，为今后类似设计工作中导流方案的选择提供一定参考依据和思路。