基于性能退化模型的船舶部件视情维修决策优化

林 程，魏汝祥，蒋铁军

(海军工程大学，湖北 武汉 430033)

性能退化失效是船舶部件主要的失效模式之一，它是指表征部件性能的参数会随着部件运行时间增加而逐渐下降，当该参数不断下降并超过指定阈值时，则认为该部件丧失功能而发生失效[1]。船舶使用环境复杂，离岸维修困难，因此在运行过程中难以保持稳定的可靠性，是典型的性能退化装备。近年来，随着海军任务的拓展和作战能力需求的提高，船舶的使用强度在不断增大，对部件可靠性提出了更高的要求。合理有效地进行船舶部件维修决策是维持船舶部件可靠性、降低使用与保障费用的重要手段，也是目前研究的热点。

目前被广泛使用的定期维修策略，具有便于安排维修计划，方便控制维修工期、费用等优势，但具体维修活动的决策以经验为主，难以针对船舶状态灵活调整维修周期。而维修周期太长会导致“维修不足”，使船舶运行时的故障率高，造成严重的后果；周期太短会导致“维修过剩”，增加维修费用，造成不必要的浪费。视情维修是目前维修领域研究的重点，是解决部件维修问题的一种有效方法[2]，有效弥补了定期维修策略的不足。

1 基于平稳维纳过程的性能退化模型

1.1 船舶部件性能退化过程建模

国内外针对船舶等复杂机械系统部件的失效过程，建立了多种性能退化模型进行描述，例如非齐次泊松过程[3]、马尔可夫过程[4]、随机差分模型[5]、基于随机过程的性能退化模型[6]等。由于随机过程模型能对时间的相关性进行有效地描述，加上复杂机械系统内部材料不均匀或外部载荷的不确定性均存在一定的随机性，近年来随机过程模型在国内外性能退化研究中较为普遍[7]。

在随机过程中，伽马过程与维纳过程是常用的描述系统退化的随机过程模型。伽马过程具有随时间单调非减特性，但其为跳跃过程，且建模较复杂，涉及的参数较多，而维纳过程可以描述非单调的性能退化过程，并具有良好的计算分析能力，是目前工程领域中应用最为广泛的性能退化模型[8]。在本文研究的问题中，船舶部件因受使用环境、任务状态、新旧程度等影响，在描述其性能退化过程时，需要注意其退化速度变化以及性能水平下降的随机性，因此本文运用维纳过程进行建模分析。

根据维纳过程性质，可将船舶部件退化过程设为{X(t)，t≥0}，t为船舶运行时间，X(t)为船舶部件性能退化累积量。本文假设船舶部件性能退化量满足平稳的维纳性能退化过程，则模型可记为:

X(t)=μt+σB(t),

(1)

式中，μ为漂移参数，用来控制模型退化的速度，且μ>0；σ为扩散参数，用来控制模型的随机变化，且σ<0；B(t)是标准布朗运动。

模型满足以下性质：①X(0)=0；②对于模型中任意的时刻t，性能退化累积量X(t)服从数学期望为μt，方差为σ2t的正态分布，即X(t)～N(μt,σ2t)；③{X(t),t≥0}有平稳独立增量性，即模型中任意时间间隔Δt内的性能退化累积量增量ΔX=X(t+Δt)-X(t)互相独立，且服从数学期望为μΔt，方差为σ2Δt的正态分布，即ΔX～N(μΔt,σ2Δt)。

1.2 参数估计

由模型性质③，X(t)从时刻t到时刻(t+Δt)的增量是独立的，并且服从正态分布，则可通过极大似然估计法，得到模型中参数的极大似然估计值。

船舶部件性能退化模型参数可以通过状态检测得到，具体检测方法可使用专家评估法，以部件维修如新时的性能退化量为0，以部件完全失效时的性能退化量为功能失效阈值L，对t时刻船舶部件的技战术指标进行评估，得到X(t)∈[0，L]，作为该船舶部件t时刻的性能退化累计量。

由于船舶部件具有高可靠和长寿命的特点，实践中一般采用离散、长间隔且非周期性的状态监测方法[9]，但这会使得每个船舶部件的检测次数非常有限。实践中，一般认为相同船舶部件服从相同参数的性能退化过程。因此，可以利用多艘船舶中相同船舶部件的性能退化数据来对模型的参数进行估计。

从时刻t1至tm，对n个相同的船舶部件的性能退化累积量进行m次检测，得到检测值为：

记第i个船舶部件开始运行的时刻为ti0=0，由模型性质①得，X(0)=0，所以X(ti0)=0，可记为:

ΔXij=X(tij)-X(ti(j-1)),

(2)

式中，i=1,2,…,n;j=1,2,3,…,m;tij表示第i个部件第j次检测的时刻;X(tij)表示第i个部件第j次检测出的性能退化累积量;X(ti(j-1))表示第i个部件第(j-1)次检测出的性能退化累积量；ΔXij为第i个部件在第(j-1)次检测至第j次检测之间增加的性能退化累计量。由模型性质③可得：

ΔXij～N(μΔtij,σ2Δtij),

(3)

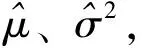
(4)

(5)

式中,tim为第i个部件进行第m次测量的时刻；X(tim)为对应的性能退化累积量检测值。

2 基于性能退化模型的视情维修决策优化

2.1 视情维修策略

视情维修是应对退化失效最有效的维修策略之一，它是指对维修对象进行状态检测和诊断，以掌握其实际性能状况和性能的发展趋势，并根据监测和诊断的结果作出合理的维修安排[10]。在视情维修理论中，存在潜在失效阈值Lp为维修决策变量，某部件的功能失效阈值为L，为固定参数，则0

在实践中，船舶部件受到自然老化与维修技术的影响，不能保证维修如新，会存在不完美维修的情况。本文认为预防性维修是不完美维修，维修后船舶部件存在剩余损伤[11]，具体表现如下。

1)经过预防性维修后，船舶部件仍具有退化累积量，并且剩余损伤的大小与维修前舰船部件具有的退化累积量成正比，比例系数为β。

2)船舶部件进行预防性维修的次数到达N*后，当下一次t=inf{t|X(t)≥Lp}时，船舶部件进行修复性维修，维修费用率为Cf，维修时间为tf。修复性维修为直接更换部件，可视为维修如新，维修后船舶部件的性能退化累积量为0，且tf>tp，Cf>Cp。

基于性能退化过程的视情维修策略见图1。

图1 基于性能退化过程的视情维修策略

图1中，船舶从t0开始运行，视情维修决策优化周期为T。t0至t1为船舶部件运行时间，在t1到达潜在失效阈值Lp时，进行预防性维修，维修时间tp=(t1-t0)α;在t2维修结束时，t2=t1+tp，此时船舶部件存在剩余损伤，大小为β·Lp；当船舶部件运行到t3时，其性能退化累积量到达潜在失效阈值Lp，假设预防性维修的次数阈值N*为1，则从t3开始进行修复性维修；在t4维修完毕，t4=t3+tf，继续运行至优化周期T结束。

2.2 优化目标与假设

在实践中，对船舶部件进行视情维修决策需要统筹考虑多艘船舶，以及维修资源限制，船舶在航率等约束条件。因此，可以调整船舶部件的潜在失效阈值Lp，来优化船舶部件视情维修决策，以满足优化目标与约束条件。根据视情维修模型，作出如下假设：①船舶部件均服从平稳的维纳性能退化过程；②船舶均是从全新开始服役，在维修决策优化期间不退役；③船舶部件性能退化量到达阈值时能被及时检测到。

以Cmin为目标函数，建立优化模型如下：

(6)

(7)

对优化模型的解释如下。

(1)该模型对n个相同的船舶部件进行视情维修决策优化，这些部件被分别安装在n艘船上，即每艘船安装一个部件。整个优化周期持续的时间为T，单位为“月”，由于各维修策略的优化周期相同，因此将总维修费用Cmin作为优化目标。

(2)在整个优化周期内，第i个船舶部件进行预防性维修的月数总和为Pi，修复性维修的月数总和为Fi。

(3)在整个优化周期内，第i艘船在航时间为Tri，维修时间为Tdi，Hi为第i艘船在航率的最低要求。

(4)在整个优化周期内，Rj为第j个月在航船数量，Dj为第j个月维修船数量，Hj为第j个月内船舶在航率的最低要求。

3 算例分析

共有10个相同部件，分别安装在10艘船上，现需要制定这些部件未来5年内的视情维修计划，要求各艘船舶的在航率不低于60%，在每一个月内至少保证5艘在航的船舶。每个部件的预防性维修费用为50万元/月，预防性维修时间的比例系数α=25%，预防性维修后的剩余损失比例系数β=10%，预防性维修次数阈值N*为10，单次修复性维修费用为500万元/月，维修时间为6个月。船舶部件性能退化量失效阈值L=10。

任取5个部件分别从时刻t1至t10，且t1

表1 部件性能退化量数据

图2 适应度变化曲线图

该视情维修决策优化模型在满足了各项约束条件的同时，使整体维修费用最低，为船舶维修实践提供了参考的思路。

4 结束语

本文建立了服从平稳维纳过程的船舶部件性能退化模型，并基于该性能退化模型研究建立了船舶部件视情维修决策优化模型，最后运用粒子群算法对算例进行了维修决策优化。结果表明，本文的优化模型具有一定的理论与现实意义，对提高船舶部件可靠性、降低维修费用具有重要作用。同时也存在一些不足，例如假设性过强，部件性能难以一直保持平稳退化，因此本文模型还可以进一步研究，提高准确性。