外辐射源雷达椭圆定位算法仿真及误差分析
唐思圆,凌 翔
(中国电子科技集团公司第三十八研究所,安徽 合肥230088)
0 引言
外辐射源雷达是一种特殊体制下的双基地雷达,其发射站为位置已知的广播电视发射台或者其他非合作的无线电发射设备,接收站为外辐射源雷达,接收目标的反射回波,并完成对目标的定位、跟踪等处理[1-2]。外辐射源雷达具有探测范围广、反隐身能力强、生存能力强等优点。在分布式外辐射源雷达系统中,通过多个辐射源或接收站的分散式部署,不仅能够提高系统的空域覆盖范围,也可以提高重叠覆盖区域的定位精度[3-5]。
外辐射源雷达的目标到接收站距离无法直接测得,需要借助其他的测量量,通过基于空间几何约束关系解算获得。常用测距方法有距离和-角度(椭圆定位算法)、角度-角度以及双曲定位等方法[6-8]。由于外辐射源雷达工作在低频波段,使得天线波束的测向能力不强,导致到达方位角的测量精度不高。而基于频率变化率的定位方法[9],由于频率变化率在某些情况下(如目标径向或接近径向时)非常小,难以准确获取,因此也有一定的局限性。在基于到达时间测量的外辐射源雷达中,每个发射站信号经目标反射后到达接收站的时间(即距离和)会形成一个椭球面,多个发射站-目标-接收站组合对就形成多个交叉椭球面,可利用多个椭球面交叉进行目标定位。由于外辐射源雷达中到达时间的测量精度较高,因此能够获得较好的定位效果。
本文中研究二维平面内的椭圆定位算法[10]及定位精度分析。通过Matlab工具构建仿真实验场景,并进行椭圆定位算法定位精度研究。通过实验分析发现,椭圆定位算法的目标定位精度不仅与雷达自身的测距精度有关,还与发射站和接收站的布站位置相关,具体实验结论为:椭圆定位算法的定位精度与发射站和接收站之间的距离有关,距离越远,则定位精度越高。
1 问题描述
本文只讨论雷达系统中含有2个发射站和一个接收站(T2R型雷达系统)情况下的椭圆定位算法。椭圆定位算法原理图如图 1所示,R为雷达系统中的接收站,T1和T2分别为2个发射站,接收站和发射站的位置已知,分别为R(x0,y0),T1(x1,y1)和T2(x2,y2),因此可以计算出发射站T1和接收站R之间的距离L1,以及发射站T2和接收站R之间的距离L2;再通过测量同一信号经目标反射及由发射站直达接收站的时间差,可以间接测量出目标距离发射站T1和接收站R的距离和r1+r0,以及目标距离发射站T2和接收站R的距离和r2+r0。而目标O应位于以R和T1为焦点的椭圆以及以R和T2为焦点的椭圆的交汇处。
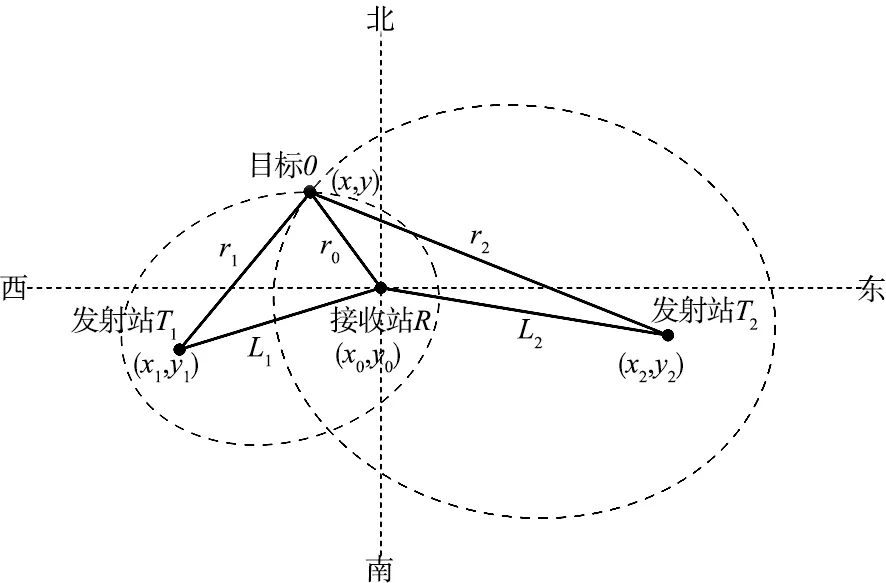
图1 椭圆定位算法原理Fig.1 Schematic diagram of ellipse location algorithm
设雷达系统接收到的目标方位角为θ,则距离和-角度定位问题可以描述为:根据上述已知接收站位置R(x0,y0),发射站位置T1(x1,y1)和T2(x2,y2),R和T1的距离和r1+r0,R和T2的距离和r2+r0,以及目标方位信息θ,求解目标O的位置(x,y) 。
2 椭圆定位算法
2.1 算法原理
在二维平面内,多个外辐射源信号到达接收站的距离和确定了以发射站和接收站为焦点的多个椭圆,解算椭圆之间的交点就可以确定目标的位置。
设一个多基地系统中,接收站为(x0,y0) ,发射站为(xi,yi)(i=1,2), 目标位置为(x,y)。r0表示目标到接收站的距离,ri表示目标到发射站i的距离,rsi表示目标到接收站和第i(i=1,2)个发射站之间的距离和。则:
(1)
相对于TR(一个发射站和一个接收站)系统常用的角度/距离和定位方法,利用接收站采集到的多个外辐射源的距离和进行定位,最大优点是定位精度高。对式(1)整理化简可以得到:
(x0-xi)x+(y0-yi)y=ki-r0rsi,
(2)
(3)
将r0看作已知量,因此可以得到如下矩阵表达式:
Ax=B,
式中,
(4)
通过最小二乘求解x,即:
x=A-1B。
(5)
令:
(6)
得到目标估计位置:
(7)
式中,
(8)
(9)
将x,y代入式(1)的第一个式子中,得:
(10)
式中,
(11)
将式(10)代入式(9),可以得到一个一元二次方程,而r0就是这个方程的解。设:
Δ=4b2-4ac。
(12)
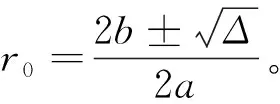
如果Δ=0,则r0只有一个唯一解;如果Δ>0,则r0存在2个解;而如果Δ<0,则r0没有解。当r0只有一个解时可以求出目标的位置信息(x,y);而如果r0有2个解,则需要解模糊。
2.2 目标定位解模糊
当使用2.1节中的方法求解得到2个解时,需要根据目标的方位角解模糊。
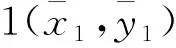
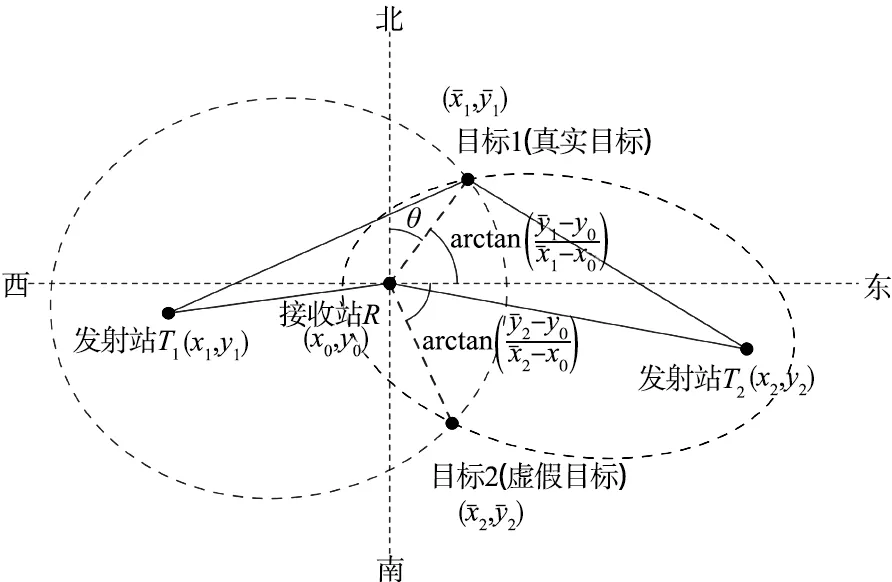
图2 方位角解模糊原理Fig.2 Schematic diagram of azimuth ambiguity resolution
则目标解模糊的计算方法为:
式中,Δθ为雷达允许的最大方位角误差。通过判断上式中哪一个不等式成立,可以知道哪个解是雷达感知到的真实目标。
3 仿真实验及结果
本文采用Matlab工具进行了椭圆定位算法仿真实验,来验证文中椭圆定位算法的有效性,并对算法定位精度进行了分析。
3.1 仿真实验
仿真实验设置为:在100 km×100 km的实验区域内,随机生成一条目标运动轨迹。目标从点(53 639,21 769)开始,沿运动轨迹匀速运动到点(89 626,96 997),目标运动轨迹如图 3所示。
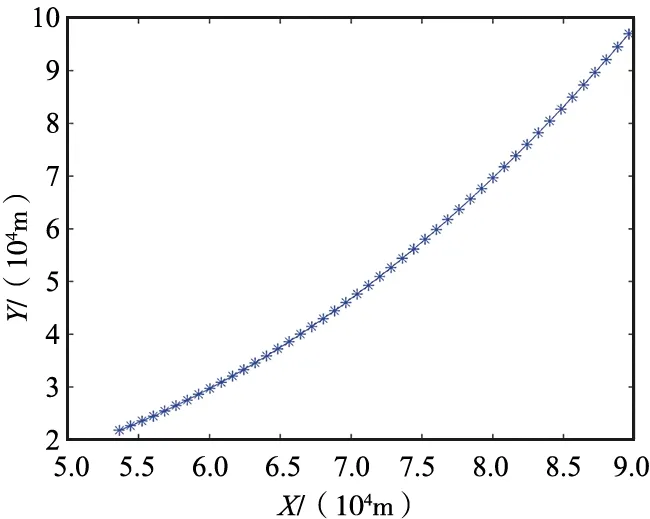
图3 模拟目标运动轨迹Fig.3 Simulation of target trajectory
由第2节中的问题描述可知,接收站R可以获得目标到发射站T1,T2和目标到接收站的距离之和r1+r0,r2+r0,以及目标的方位角θ,设雷达方位角测量精度为1°(100 km),距离测量精度为200 m(100 km),且误差满足正态分布。
设接收站R位于坐标(50 000,0)处,发射站T1位于坐标(20 000,0)处、发射站T2位于坐标(80 000,5 000)处,则椭圆定位算法的计算结果如图 4所示。从图4中可以看出,椭圆定位算法能够较精确地定位出目标位置。
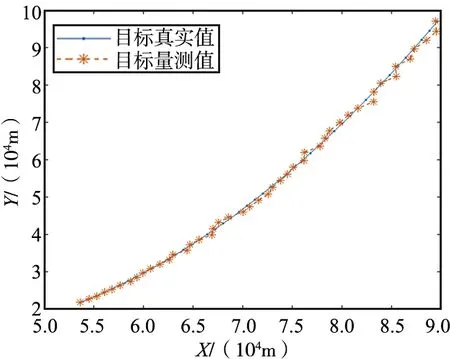
图4 椭圆定位算法目标定位结果Fig.4 Target location result of ellipse location algorithm
3.2 误差分析
式中,
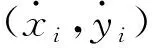
图5给出了椭圆定位算法误差结果。通过实验误差进行分析可以得到,X轴的定位误差为:328.892 6 m,Y轴的定位误差为163.019 9 m。
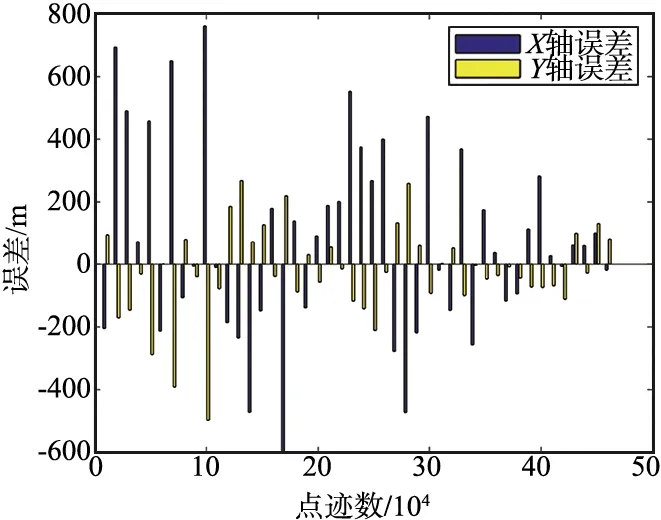
图5 椭圆定位算法误差结果Fig.5 Error result of ellipse location algorithm
3.3 定位精度分析
通过Matlab仿真实验研究椭圆定位算法定位目标误差精度受发射站和接收站之间的距离的影响。设目标运动轨迹和雷达参数满足3.1节中的设定,且接收站R位于坐标(50 000,0)处,分别计算发射站T1,T2部署于不同位置时的目标定位误差。实验结果如图 6所示。
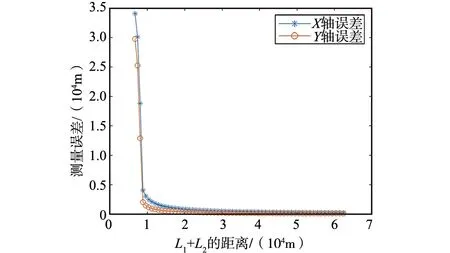
图6 定位精度与雷达站距离之间的关系Fig.6 Relationship between location accuracy and distance of radar station
X轴为发射站T1,T2与接收站R之间的距离之和,即图 1中的L1+L2,Y轴为根据3.2节方法计算得到的定位误差。可以看出,椭圆定位算法的定位误差随L1+L2的增长呈指数减小。因此可以看出当发射站和接收站之间的距离越远时,椭圆定位算法的定位精度越高。
4 结束语
椭圆定位算法是外辐射源雷达中常用的目标测距方法,通过该算法可以实现目标的高精度测距。本文中研究二维平面内的椭圆定位算法及定位精度分析。通过Matlab仿真实验发现椭圆定位算法可较精确地计算得到目标的真实位置,且目标定位精度与发射站和接收站之间的距离有关。通过实验可知,定位误差随雷达站之间距离的增加呈指数减小,即雷达站之间的距离越远,则定位精度越高。

