磁斯格明子研究现状综述

杨洪新

（1.中国科学院 宁波材料技术与工程研究所，浙江 宁波315201； 2.中国科学院大学 材料科学与光电技术学院，北京100049）

1962年，英国核物理学家Skyrme［1］在研究介子与重子间相互作用的统一场理论时，提出一种具有拓扑性的准粒子结构，即斯格明子.此后，人们在液晶［2］、玻色-爱因斯坦凝聚［3］以及量子霍尔体系［4］等不同研究领域中均发现了斯格明子的存在，在凝聚态物理领域，磁斯格明子更是引起了人们的广泛关注，这不仅是因为磁斯格明子的基础物理研究价值，更重要的是人们期望其新颖的自旋结构表现出的丰富物性在信息存储和逻辑器件等方面有重要的应用，因而在理论研究和实验观测磁斯格明子等方面都涌现出很多突破性进展.早在1975年，Belavin等［5］在理论上预测了一种存在于二维Heisenberg自旋系统的亚稳态，其自旋结构与Skyrme提出的斯格明子一致.这是在磁性系统中首次提出磁斯格明子的概念.1985年，Klebanov［6］将斯格明子整齐地排列到简单立方晶格位置上，并发现斯格明子可以旋转，从而被最近邻的6个斯格明子所吸引.1988年，Kugler等［7］考虑一种由适当旋转的半斯格明子组成的简单立方晶体，结合晶体对称性等方法计算发现该立方晶体比Klebanov晶体能量还低，从而预言了一种新的斯格明子晶体.1993年，Sondhi等［4］研究了当填充因子υ＝1且赛曼能和典型的相互作用能处于任意比列时，二维电子气在高磁场下的物理本质.通过理论计算表明：当塞曼劈裂很小时，体系呈现非平庸的宏观有序自旋结构，即为斯格明子.直到2006年，Rößler等［8］才首次从理论上预言了自发稳定存在的磁斯格明子态广泛地存在于具备空间反演对称性破缺的磁性薄膜或手性磁体中.

在理论研究取得一系列突破性进展后，2009年，Mühlbauer等［9］通过小角度中子衍射实验观察到MnSi单晶中其“A”相存在的温度-磁场区域有6个衍射斑点，如图1（a）所示，并最终确认了MnSi单晶中的“A”相即为拓扑稳定的磁斯格明子的磁序结构.这是在实验上首次证实了磁斯格明子的存在.随后，Yu等［10］利用洛仑兹透射电子显微镜在Fe1-xCoxSi单晶样品中实现了实空间的斯格明子磁成像，其实验结果和蒙特卡罗模拟的结果如图1（b）和（c）所示.2011年，Heinze等［11］在Fe/Ir（111）磁性薄膜体系中也观测到自发的原子级斯格明子晶体.这些里程碑式的工作为后续磁斯格明子的发展奠定了坚实的基础.2013年，Fert等［12-13］通过微磁学模拟的方法，系统研究了单个磁斯格明子在多层膜纳米带结构中的激发、稳定性以及电流驱动现象，并首次提出磁斯格明子可以作为新一代自旋电子器件的信息存储载体.2015年，Du等［14］利用FeGe纳米带的边界效应并在外加磁场作用下实现了磁斯格明子的产生.2017年，Hsu等［15］证明了局部电场可以实现磁斯格明子与铁磁态之间的相互转换.此外，Zhou和Ezawa［16］以及Jiang等［17］分别通过模拟和实验实现了室温下受限几何结构中带状磁畴向单个磁斯格明子的转换，从而实现室温下对磁斯格明子的简单操控.最近，文献［18］在Pt/Co/Ni80Fe20/Ir20Mn80多层膜中实现了零外场下室温稳定的磁斯格明子，平均直径约为60 nm.在该体系中，交换偏置使得磁斯格明子在几十毫特斯拉外磁场的扰动下不受干扰，这对实现基于磁斯格明子的存储器件有着重要的意义.

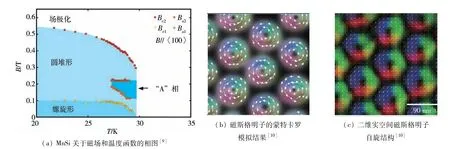
图1 磁斯格明子的实验及理论研究Fig.1 The theoretical and experimental studies of magnetic skyrmion

目前，实验上验证能存在磁斯格明子的材料体系有很多，本文主要关注3类材料体系.第一类是具有非中心对称结构的手性磁体，例如MnSi［10，19］、FeGe［20］等.在这类B20材料中，Dzyaloshinsky-Moriya相互作用（DMI）起源于晶体结构的对称性破缺，趋向形成布洛赫（Bloch）型磁斯格明子，如图2（a）和（b）.这类斯格明子通常存在于低温或接近室温的环境，且磁斯格明子的尺寸一般在10～100 nm之间.此外，β-Mn型Co-Zn-Mn合金引起人们的极大关注［21］.磁斯格明子相在该非B20的手性磁体中，可在400 K的高温下存在并具有零场稳定性.第二类材料是重金属（HM）/铁磁金属（FM）薄膜异质结.在这类材料中，DMI起源于界面反演对称性破缺，趋向形成奈尔（Néel）型磁斯格明子，如图2（c）和（d）.该类磁斯格明子最早发现于具有强界面DMI的Fe/Ir（111）薄膜结构［11］，该体系中磁斯格明子的大小仅为1 nm，是目前为止实验上观测到的尺寸最小的磁斯格明子，但是该类材料中磁斯格明子的稳定温度通常小于10 K.此外，人们利用磁控溅射生长的垂直磁性多层膜体系是研究磁斯格明子的另一个热点.比如在Pt/Co/MgO［22］纳米结构、Pt/CoFeB/MgO［23］纳米结构以及Pt/Co/Ir［24］多层膜观察到了室温磁斯格明子.有趣的是，在一些反铁磁与铁磁薄膜的异质结以及稀土亚铁磁与铁磁薄膜异质结中也观测到磁斯格明子［25-26］.第三类是二维单层磁性材料.除了传统的金属块体材料体系或薄膜体系，2020年，文献［27-28］通过第一性原理计算和微磁模拟预言在二维磁性Janus结构中也存在磁斯格明子.这为实验上实现对磁斯格明子的产生以及操控提供更多可能的材料选择，因而具有重要的意义.

人们通过实验手段及理论计算研究磁斯格明子所取得的成就极大地推动了磁斯格明子领域的发展，并对基于磁斯格明子的电子学应用产生深远影响.由于磁斯格明子特殊的拓扑性质，并具备尺寸小、结构稳定、驱动阈值电流小等诸多优点，因而可将磁斯格明子视作基本的存储单元应用于电子学器件，比如磁斯格明子赛道存储器［12-13］、晶体管［29］、逻辑器件［30］以及自旋纳米振荡器［31］等.更重要的是，人们具有多种操纵磁斯格明子形态以及运动的实验技术［32-33］，这无疑大大提升磁斯格明子的应用前景.本综述简单介绍了磁斯格明子的发展历程，归纳总结了磁斯格明子的材料体系、研究方法和基于磁斯格明子的电子学器件，着重介绍从第一性原理计算的角度出发探讨界面DMI物理本质.

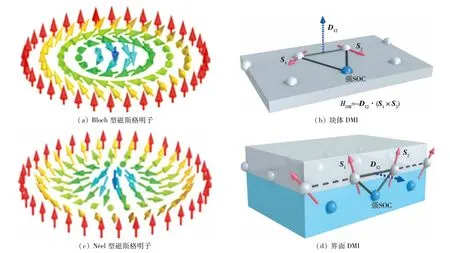
图2 磁斯格明子结构以及DMI示意图［12］Fig.2 Structures of magntic skyrmion and schematics of DMI［12］

1 磁斯格明子的拓扑物理性质

1.1 磁斯格明子拓扑稳定性磁斯格明子是一种受拓扑保护的磁涡旋结构，并通过拓扑数（斯格明子数）来定义：

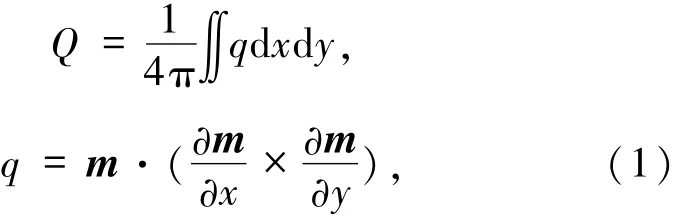
其中，q为拓扑密度，m为归一化磁矩.当磁结构的拓扑数为±1时，则认为这个自旋磁结构是磁斯格明子［34］.磁斯格明子内的自旋以固定的手性从边界区域的向上排列连续地旋转到其中心区域的向下排列，这使得边界区域和中心区域的自旋方向相反，且中间过渡区域自旋有不同的旋转取向，从而区分不同类型的磁斯格明子.典型的磁斯格明子种类包括Bloch型和Néel型.类比于磁畴壁，通过考察磁斯格明子的径向剖面可发现，如果自旋旋转面垂直于截面，则为Bloch型磁斯格明子（图2（a））；如果自旋旋转面是平行于截面，则为Néel型磁斯格明子（图2（b））.虽然2种磁斯格明子的自旋构型不同，但是两者可以通过连续形变相互转化.因此，这2种构型是拓扑等价的.自旋间各相互作用的竞争会导致不同的自旋排布方式.当考虑二维体系时，若以磁斯格明子这种非共线自旋结构作为整个结构体系自旋排布的基态时，它要比最近邻自旋形成的有序结构的能量低.因而从能量的角度看，不同态在相互转变中需要克服一定的势垒，这就为磁斯格明子的稳定性提供了充足保证.另一方面，从拓扑的角度来分析，在绝热近似和自旋连续转动的条件下，非平庸拓扑自旋结构和平庸拓扑自旋结构无法相互转换［35］，意味着无法在绝热近似下通过连续的自旋转动变化来完成磁斯格明子的产生和湮灭过程.因此，斯格明子的拓扑自旋结构是受到拓扑保护的，增加了其稳定性.在实验方面发现诸如MnSi单晶等B20结构磁体中就可以长期存在亚稳态磁斯格明子［10，19］，从而证明了其拓扑稳定性.

1.2 拓扑霍尔效应根据磁斯格明子非共线的自旋构型，若考虑传导电子与磁斯格明子的相互作用，将会得到很多有趣的物理效应.当一个传导电子穿越磁斯格明子时，其自旋方向在入射和出射时总是平行排列，这符合由洪德定则描述的载流子自旋总是试图与所处位置的局域电子的自旋保持平行［36］.然而，在穿越过程中传导电子与磁斯格明子内部的局域自旋发生耦合，这导致自由电子的自旋方向将不断翻转变化.若将这样的翻转过程等效为一个磁场，这种等效磁场会影响电子的运动轨迹并给传导电子的霍尔效应产生额外的贡献，被称为拓扑霍尔效应［37］.该等效磁场，即emergent磁场bz［38］可表示为

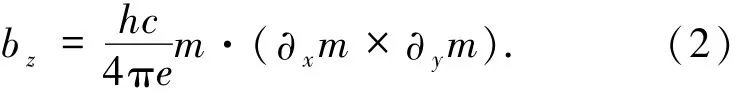
对比（1）式中计算的拓扑荷Q可以发现，emergent磁场强度正比于拓扑荷，即bz∝Q，因而与磁斯格明子的拓扑性相关.当磁斯格明子以一定速度运动时，运动的emergent磁场还产生一个电场，图3则显示了在复合场作用下将产生一个偏转.拓扑霍尔效应有着重要的意义，它与磁斯格明子的拓扑非平庸性紧密相连，可以借此实现对由DMI主导的磁斯格明子的探测［39］.实际上，一些具有标量自旋手性结构的磁体中也会引起拓扑霍尔效应［40-41］.

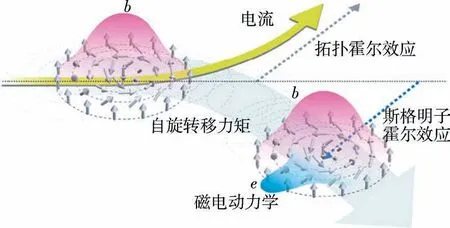
图3 磁斯格明子与电流相互作用产生的拓扑霍尔效应以及斯格明子霍尔效应示意图［34］Fig.3 Schematic of skyrmion motion and associated to pological Hall effect and skyrmion Hall effect under the flow of electrons［34］

1.3 斯格明子霍尔效应当传导电子穿越磁斯格明子时受到拓扑霍尔效应产生偏转，而磁斯格明子也会在传导电子的反作用下，即马格努斯力［34］的作用下产生额外的横向速度，从而向另一侧发生偏转，如图3所示.这个效应则是斯格明子霍尔效应.带电粒子在磁场中运动会产生霍尔效应，其中电荷的正负性决定带电粒子的偏离方向.类似地，磁斯格明子在电场驱动下会产生斯格明子霍尔效应.因此，磁斯格明子拓扑荷的正负性也将决定磁斯格明子的偏转方向［42］.

2 磁斯格明子与Dzyaloshinskii-Moriya相互作用

磁有序系统中稳定磁斯格明子的机理主要包括以下4种：1）长程磁偶极相互作用［43-44］；2）DM相互作用（DMI）［45-46］；3）阻挫交换相互作用［47］；4）四自旋交换相互作用［11］.在1）和2）情况下，磁斯格明子及其阵列尺寸大于晶格常数，满足连续性近似条件且相应的磁斯格明子能量密度远小于原子间的交换能J，使得该类型磁斯格明子能够被相对容易地产生及消灭，且更容易操控，因而广受专注.首先对于长程磁偶极相互作用而言，它与垂直磁各向异性形成竞争而产生的周期性磁条带会在外加垂直磁场的诱导下转化为原子级斯格明子晶格，而由DMI诱导产生的磁斯格明子则来源于晶体结构的对称性破缺以及自旋轨道耦合（SOC）.在中心对称结构破缺的磁性体系中，由于海森堡交换相互作用和DMI的相互竞争使得磁斯格明子在铁磁态背景中所具有的能量最低，进而使其能够稳定存在.

以上主要的4种机制中，DMI是目前最受关注的一种机制.这是因为DMI所产生的磁斯格明子比磁偶极相互作用下的磁斯格明子尺寸以及驱动电流更小，从能源消耗的角度来看更有利于应用在基于磁斯格明子的电子器件中.在实验上常见的磁斯格明子材料中，如非中心对称的块状磁性材料（图2（c））和界面反演对称性破缺的过渡金属薄膜（图2（d）），由于这些材料中的原子排列结构对称性降低，并且存在较强的自旋轨道耦合，往往会产生很大的DMI.因此，接下来着重讨论DMI的物理机制以及不同类型界面的DMI.

2.1 DMI的形成机制DMI的发现起源于20世纪60年代科学家们对一些反铁磁材料为什么会表现出弱铁磁性的研究.在此之前，人们注意到有些被认为是反铁磁性的材料，如α-Fe2O3以及碳酸化合物MnCO3和CoCO3等，会表现出自发的磁化行为，然而它们的自发磁矩相对磁性原子的磁矩又非常小.当时有些解释认为这是由于杂质或反铁磁磁畴导致的非本征磁性性质，但是理论分析表明它们都不利于降低系统的自由能.1958年，Dzyaloshinskii［45］首先对该现象给出了正确的理论解释，提出这些反铁磁晶体中存在弱铁磁性的关键原因是它们的自由能表达式中存在如下的反对称项

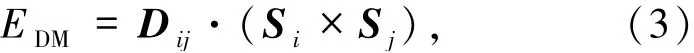
其中，Dij是矢量，Si和Sj是位置i和j上的自旋矢量，这一项后来被称为DM相互作用.从（3）式可以看到，它与使自旋平行或反平行排列的Heisenberg交换相互作用原子自旋Si和Sj之间的有效相互作用形式

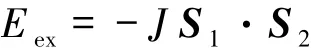
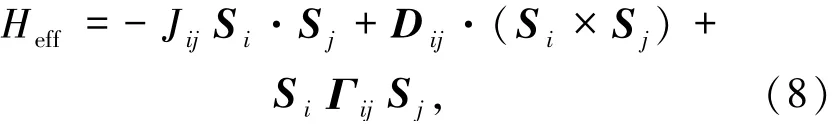
不同，而DM相互作用趋向于使相邻自旋相互垂直排列.正是这2种相互作用之间的竞争，最终导致了α-Fe2O3等反铁磁材料的自旋从共线性排列方向产生了小角度的倾斜，从而表现出弱铁磁性.从方程（3）可以看出，DMI的存在打破了自旋体系的空间反演对称性.

对于上述模型，Dzyaloshinskii［45］完全是从晶体对称性出发，利用朗道二级相变唯像理论给出的.他既没有指出这一相互作用的微观起源，也没有给出矢量Dij的具体计算方式.1960年，Moriya［46，48］把Anderson超交换相互作用理论扩展到有SOC作用的情况，证明了在中心对称性破缺的磁性绝缘体中，DMI是自旋间超交换作用和SOC共同作用的结果.对于金属体，文献［49-50］提出在无序合金中或磁性薄膜和重金属薄膜界面处，2个磁性原子之间可以通过一个有强SOC的非磁原子来传递DMI.虽然以上2个模型是从不同的磁性耦合机制出发的，但他们最终都得到了具有（3）式反对称形式的相互作用项.这间接反映出DMI在不同的磁性体系中是普遍存在的.［51］

根据Moriya理论 ，可以通过以下的简单模型来了解DM相互作用的物理来源.仅考虑2个具有3d电子轨道的磁性原子，分别位于i和j，那么这2个原子系统可以通过以下的哈密顿量描述：

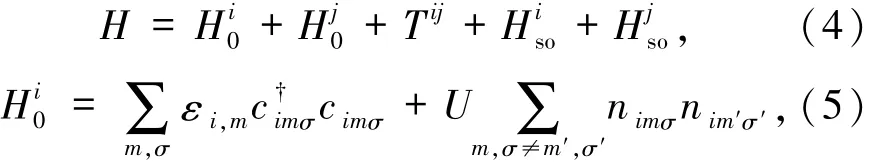
H0i表示原子i处具有Hubbard相互作用的3d电子状态，εi，m是3d电子轨道能量，U是电子间库伦排斥能；

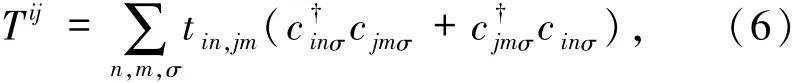
Tij描述了2原子之间的电子跃迁，tin，jm是原子i处的轨道n和原子j处的轨道m之间的跃迁积分；

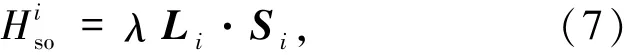
Hiso则是原子i处的自旋轨道耦合作用.

将系统总哈密顿量（4）式的后3项作为微扰项，那么通过依次考虑不同的微扰项，可以得到2其中，方程第一项为通常的海森堡交换相互作用，可以利用二阶微扰理论从哈密顿量Hi0+Hj0+Tij得到，交换耦合系数Jij正比于（tij）2/U；进一步考虑自旋轨道耦合项Hso，则可得到第二项DMI，矢量Dij正比于λ（tij）2/U；方程最后一项考虑了四阶微扰项后得到的各向异性相互作用，Γij正比于λ2（tij）2/U，通常情况下比DMI小很多.由此，可以得到如下的物理图像：在没有SOC时，电子在近邻原子之间跃迁时不改变自旋，并且由于超交换相互作用，近邻自旋呈共线磁性耦合；但是考虑了SOC后，电子在跃迁过程中会使自旋发生偏转.因此，系统的基态为自旋倾斜的非共线磁耦合.由此可见，DMI的本质是晶体空间反演对称性破缺后自旋轨道耦合作用的高阶效应.

2.2 界面DMI近几年来，相对于块体材料，低维体系的磁性性质受到了研究者们的广泛关注.因为低维材料不仅更有利于器件的小型化，提高集成度，并且在其低维化的过程中会出现许多新奇的磁性性质，尤其是人们在磁性薄膜材料中成功诱导出了室温磁斯格明子，这为磁斯格明子迈向实用化铺平了道路.在这低维磁性体系中，界面DMI是磁斯格明子存在的关键因素.因此，精确地测量、调控材料中的DMI以及寻找新的DMI材料对于斯格明子的研究至关重要.目前，实验上有多种研究DMI的方法，比如研究磁畴壁在电流驱动下的动力学过程，间接地判断材料中DMI的符号［52］；或者是通过数值拟合薄膜中磁畴尺寸和外磁场的依赖关系提取出DMI的绝对值［53］；再者利用布里渊光散射方法直接测量薄膜异质结中的界面DMI常数［54］.另一方面，通过理论计算研究界面DMI也取得很多突破性成果［55-56］，它清晰地给出体系中DMI的起源以及体系中不同原子对DMI的贡献大小.因此，接下来将结合之前的工作从第一性原理的角度去理解层间DMI的物理本质.

通过上述关于DMI形成机制的讨论，知道在一个缺少空间反演对称性的多层膜体系中，材料的自旋轨道耦合会导致产生一个非对称的交换相互作用，即DMI（HDMI），其形式可简述为

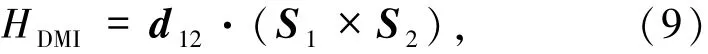
其中，S1和S2是2个相邻的自旋磁矩；d12是相应的DMI矢量.对于界面DMI的情况其表达式为

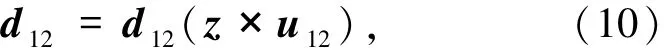
其中，u12是连接2个自旋磁矩S1和S2的单位位移矢量，d12的正负与材料自身性质相关.对于d12＞0，d12的方向与图2（d）虚线箭头反向，故为了降低HDMI能量，从S1到S2自旋取向应当按逆时针旋转.同理，对于d12＜0，d12的方向与图中虚线箭头同向，则S1到S2自旋取向应当按顺时针方向旋转.根据薄膜材料中SOC的来源可将DMI分为2种类型：Fert-Levy型和Rashba型.

2.2.1 Fert-Levy型DMI （I）HM/FM界面的DMI.根据Fert-Levy模型，磁性原子之间可以通过具有强SOC的重元素来传递DMI.因此，在HM/FM界面处有可能产生较强的DMI.2007年，Bode等［57］利用自旋极化扫描隧道显微镜在Mn/W（110）超薄薄膜上首次证实了界面DMI的存在.随后人们对不同材料组成的HM/FM异质结的磁性性质作了大量的研究，并发现DMI在这种结构中是广泛存在的.许多实验研究表明，FM/HM界面处的DMI的手性和大小等性质与所用的材料及界面结构密切相关［58-59］.为了更好地控制DMI的手性和大小等性质，需要了解界面DMI与薄膜层厚之间所存在的关系，以及其空间分布和对应的电子能量来源位置等性质.下面通过典型的HM/FM异质结Co/Pt薄膜以及二维单层Janus MnXY（X，Y＝S，Se，Te，X≠Y）结构来说明界面DMI的性质.

作为目前最精确的计算手段之一，基于密度泛函理论的第一性原理计算为深入了解界面DMI提供了一个很好的途径.通过第一性原理计算，可以预言许多实验上难以获得的DMI性质.从（3）式中看到，DMI能量是与体系的自旋构型手性相关的.因此，可以通过计算具有不同手性的自旋构型的总能量来提取体系的DM矢量Dij.以Co（3）/Pt（3）界面为例，图4（a）给出了在计算中所采用的按顺时针和反时针旋转的自旋构型，它们的能量分别为ECW和EACW，那么通过（3）式可以得到总的DMI系数dtot，即

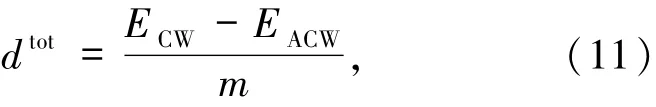
其中，dtot的符号决定了DMI矢量的手性，dtot＞0表示反时针手性，dtot＜0表示顺时针手性；m是由自旋螺旋周期决定的常数，对于图4中周期为4个原子间距的自旋构型m＝12.通过dtot也可以很容易得到微磁模拟中常用的把能量平均到单位体积的DMI系数D，这一系数通常与铁磁层厚度成反比.另外，如图4（b）所示，如果仅使第k层的磁性原子自旋形成螺旋构型，而其他层的磁矩与之垂直，那么就可以得到层分辨的DMI值dk.进一步，可以通过计算出在不同自旋螺旋手性时第k′层原子的SOC能量差ΔEk，k′SOC来了解dk的能量来源分布.

图4（c）和（d）给出了Co（3）/Pt（3）界面的dk和ΔEk，k′SOC计算结果.很明显地看到，dk主要集中在界面处的Co1层，而在离开界面的Co2和Co3层界面处dk急剧减小并且为负号.此外，Pt1处的dk值很小，Pt2和Pt3处则可以忽略不计，这说明DMI是一种界面效应.现在考察DMI的能量来源.首先对于DMI值dk最大的k＝Co（1），与其相关的最大SOC能量差ΔECo（1），Pt（1）SOC来源于近邻的Pt（1）层，这与Fert-Levy模型给出的结果是一致的，即对于Co-Pt-Co这一典型的非中心对称3原子构型，2个Co原子之间的自旋手性的改变会导致Pt的SOC能量发生改变.而对于远离界面Pt的Co3层，其较小的DMI则来源于Co2和Co1层较小的SOC能量差.类似地，Co2层DMI来源于Co1层及Pt1和Pt2层.对于由近邻效应引起的非常小的Pt1自旋，其DMI来源于其他Pt层的SOC能量差.

图4（e）给出了采用不同层厚和重金属材料时的总DMI强度.对于Co/Pt异质结，可以看到随着Co或Pt层厚的变化，其DMI强度在2.5～5.2 meV的范围内变化，并且其手性都是反时针的.还可以看到，除了Co（1）/Pt（N）结构，其他结构的DMI值随Pt厚度变化都很小.整体上在厚度较大时dtot趋向于恒定值.对于微磁模拟DMI系数D，其随层厚变化与预期的一样，随层厚增加而减小.另外，对于实验中可能存在的Co和Pt原子界面混合情况，DMI强度差不多减小了一半.如果把重金属层替换为其他材料，如Au、Ir、Pd等，DMI也会发生变化，特别是对于Au和Ir，DMI手性变成了顺时针.

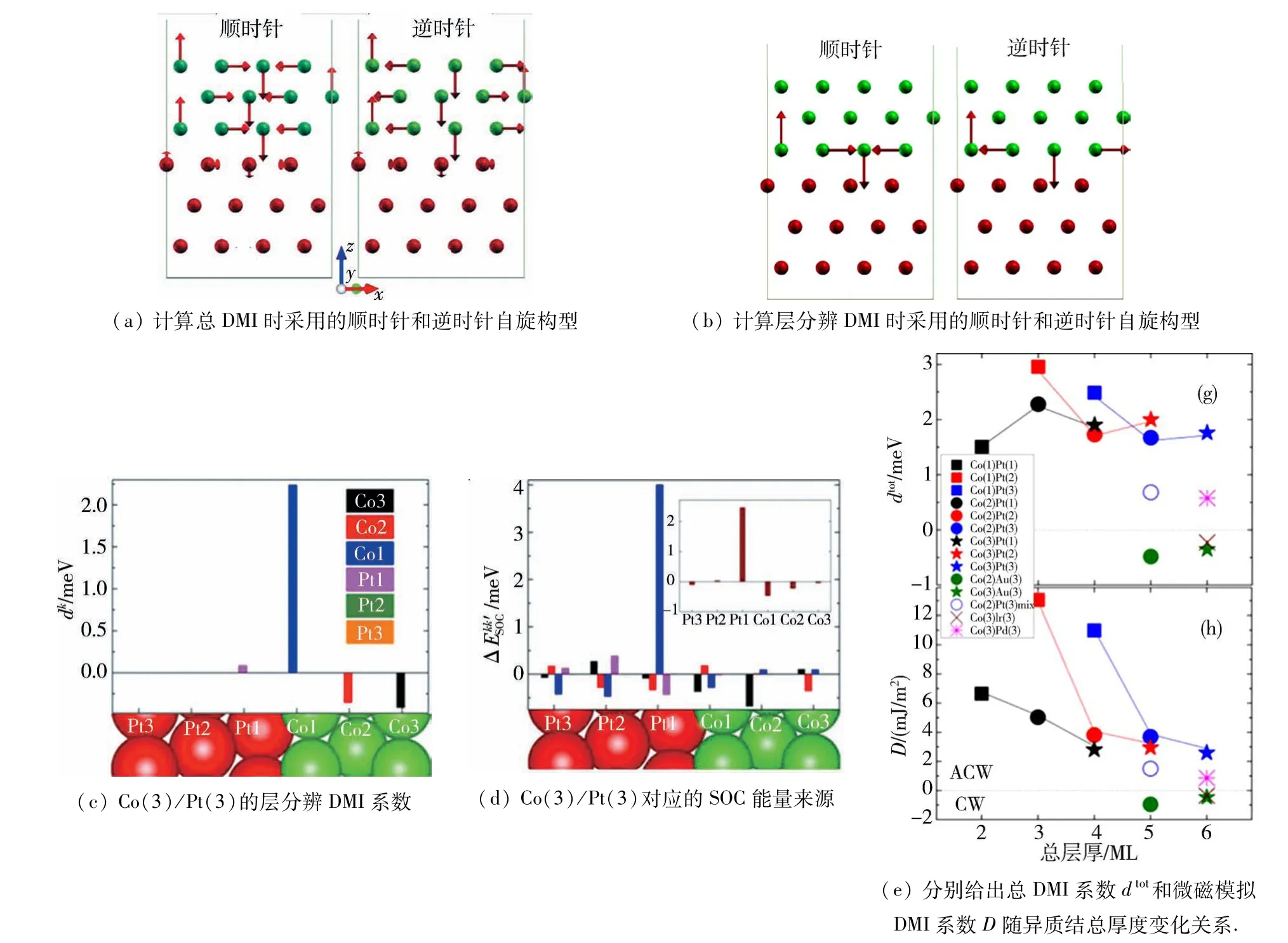
图4 铁磁金属和重金属界面的DMI［55］Fig.4 The interfacial DMI between ferromagnetic metal and heavy metal［55］

通过以上的计算，可以清楚地了解到在FM/HM异质结中DMI与薄膜层厚之间关系，以及其空间分布和能量来源位置等性质.目前已有大量的实验［60-61］测量了不同FM/HM结构的DMI性质，实验测量值与前面的理论预测值是一致的，表明这些理论计算不仅可以为理解DMI的本质提供清晰的物理图像，也为实验上进一步对DMI进行调控提供了可靠的理论依据.

（II）二维磁性Janus结构的DMI.除了上述介绍的HM/FM界面的Fert-levy型DMI，二维磁性材料中也能存在该类型的DMI.以Janus MnXY（X，Y＝S，Se，Te，X≠Y）结构为例，图5（a）给出了在计算中所采用的晶体结构.对于Mn原子，可以从图5（a）知道形成了对称性为C3v的六角结构，并且被夹在2层不同硫族元素的中间.在计算的时候，始终把较轻的X原子置于顶层而把更重的Y原子放在底层，这样在Janus MnXY体系中的上下2层原子的不对称性以及体系中存在的SOC将使整个体系产生较大DMI.

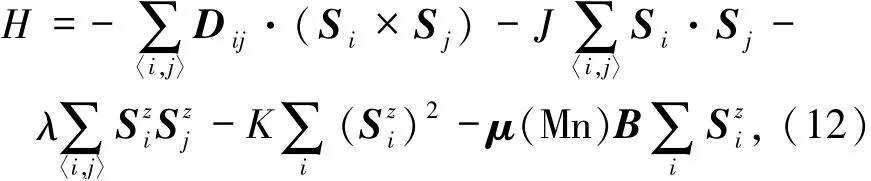
对于Janus MnXY（X，Y＝S，Se，Te，X≠Y）体系，其自旋哈密顿量可表示为其中，三维单位矢量Si代表第i个Mn原子的自旋方向，〈i，j〉代表最近邻Mn原子对的自旋方向.等式右边的前4项分别是DMI、海森堡交换作用、各向异性对称交换作用以及易轴单粒子各向异性，并分别由参数Dij、J、λ和K来表示.最后一项是塞曼能，其中μ（Mn）和B分别代表Mn原子的磁矩和外磁场.接下来着重探讨最感兴趣的DMI.根据Moriya的对称性原则，由于镜面穿过两邻近Mn原子的键的中间，因而其每对最近邻Mn原子DMI矢量Dij垂直于该键.此时

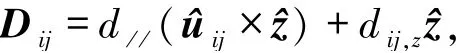
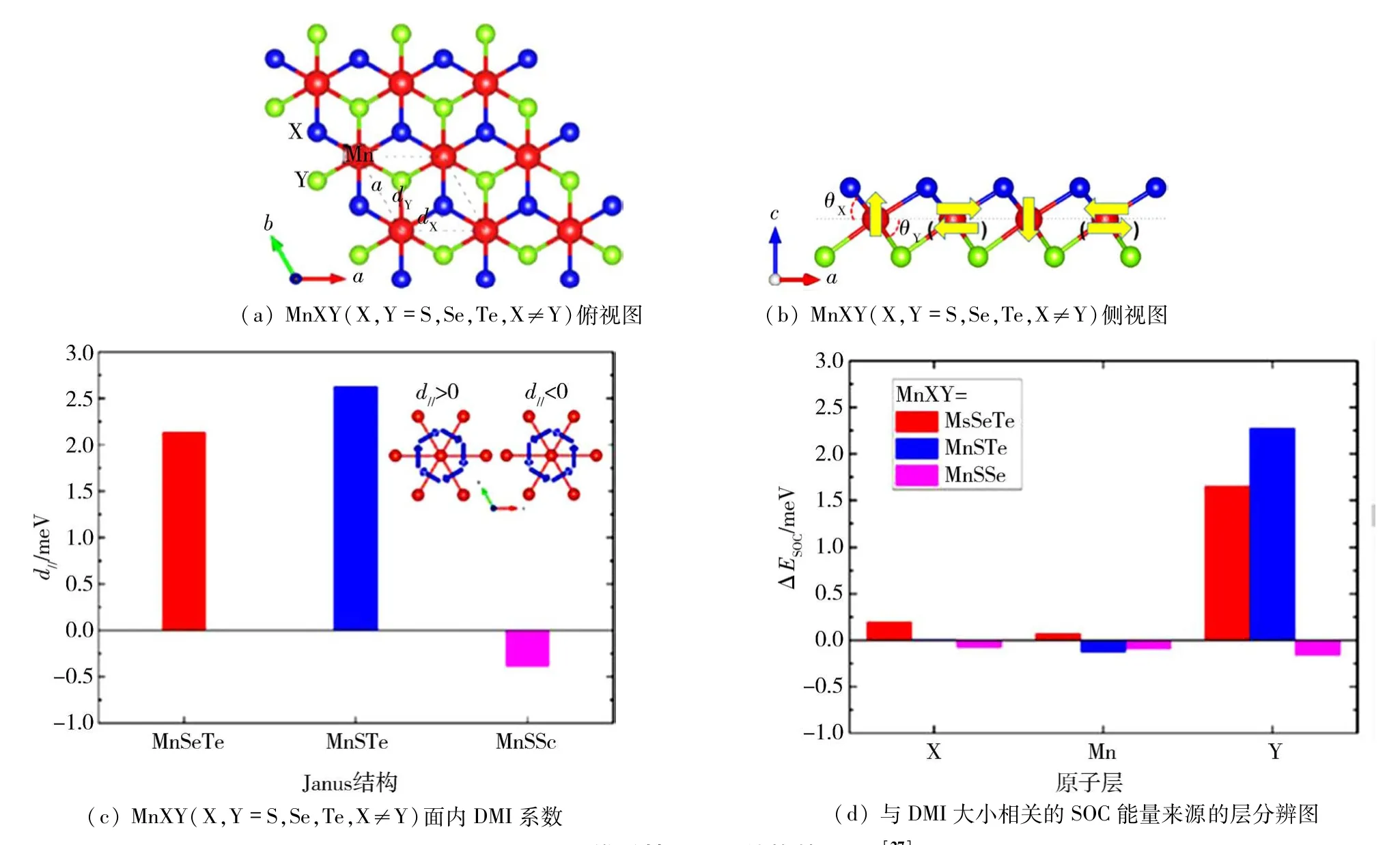
图5 二维磁性Janus结构的DMI［27］Fig.5 The DMI of two-dimensional magnetic Janus structure［27］

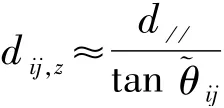
给出，其中

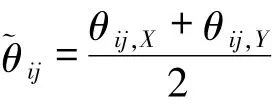
代表（Mn）i-X（Y）-（Mn）j原子倾斜平面的平均值.

如图5（b）所示，标注出单层Janus MnXY的面内DMI分量d//的值，其中的2种手性自旋结构系统表达了最近邻Mn原子间DMI矢量Dij方向.更重要的是，如图5（c）所示，可以看到所有的单层Janus MnXY结构具有很强的DMI，尤其是MnSeTe和MnSTe的面内分量d//达到2.14和2.63 meV.和传统的HM/FM异质结结构的DMI大小相比，比如Co/Pt薄 膜（3.0 meV）［62］和Fe/Ir（111）薄 膜（1.7 meV）［63］，上述2个结构的DMI的值完全可以比拟.进一步地，通过解析提取出相关的SOC能量阐明单层Janus MnXY结构中DMI的起源.如图5（d）所示，可以看见在所有MnXY结构中，主要的DMI贡献来源于最重的Y原子，尤其是在MnSeTe和MnSTe中的Te原子使得体系的DMI要比MnSSe的大很多.由此可见，单层Janus MnXY中存在Fert-Levy型的DMI.类比于5d过渡金属在FM/HM中自旋轨道相互作用的贡献，这是由于在单层Janus MnXY中硫族元素作为自旋轨道耦合的有效位点提供了DMI所必需的自旋轨道散射.此外，由于原子序数越大自旋轨道耦合越强，这也就解释了Te原子对DMI的贡献最大.

2.2.2 Rashba型DMI 上述介绍的Fert-Levy型DMI，对于传统的FM/HM体系要求非磁层能提供强的SOC才能获得较大的值，从而导致衬底材料多选择5d等重金属材料.但是重金属的存在，一般会影响存储器件的读写效率，并与当前工业界普遍使用的磁隧道结存储结构不兼容，使制造工艺复杂化.而对于二维磁性Janus结构，由于实验技术以及材料本身的性质限制使得很难在实验上获得较稳定的单层磁性体系.因此，人们迫切希望能够突破Fert-Levy机制来获得较大的DMI.

在异质结结构中空间反演对称性的破坏也会导致Rashba效应的出现.如果比较DMI和Rashba效应的产生条件，会发现它们之间有许多相似之处.例如，它们都要求空间反演对称性的破缺，并且SOC都起着关键性的作用.这很自然地会使人们推测如果在磁性层和非磁层中出现Rashba效应，是否也会相应地诱导出DMI.此外，人们早就知道在一些较轻元素组成的异质结中也可以实现Rashba效应［64］.因此，如果能够通过Rashba效应来诱导出DMI，那么就有可能实现前面提到的，在突破Fert-Levy机制条件下获得较大的DMI的愿景.实际上，已有不同的研究小组［65-66］通过模型推导从理论上预言Rashba效应可以诱导出DMI，并且发现DMI与Rashba系数之间存在如下的关系其中，A是自旋刚度系数，kR是由Rashba系数αR、电子有效质量me和约化Planck常数h决定的系数.由此可见，Rashba效应越强，引起的界面DMI也越大.

石墨烯独特的电子结构性质，使其在自旋电子学中有着非常重要的作用.例如，通过石墨烯可以实现量子自旋霍尔效应［67］、增强自旋注入效率［68］、提高铁磁薄膜的垂直各向异性［69］，以及产生Rashba效应［70］等.以石墨烯与三层Co组成的异质结（石墨烯/Co）为例来研究由Rashba效应引起的DMI性质.

根据前面介绍的计算不同手性自旋构型总能方法，可以分析石墨烯/Co的DMI性质，求得石墨烯/Co总DMI为0.49 meV.更值得注意的是，对比Co/Pt（图4（c）和（d））和石墨烯/Co（图6（b））结构的DMI能量来源和空间分布，可以发现石墨烯/Co的DMI形成机制完全不同于前面介绍的Fert-Levy型DMI.如前面讨论过的，在Co/Pt结构中，DMI在界面铁磁层Co层最大，而其SOC能量并非来自Co层，而是来自邻近的重金属Pt层，但是在石墨烯/Co中，DMI和SOC能量则都在Co层内.这表明了Rashba效应引起的DMI与Fert-Levy型DMI的能量来源的巨大差异.

也可以根据（13）式来估算石墨烯/Co的DMI.从石墨烯/Co的电子能带结构（图6（c））可以发现，在¯Γ附近k0＝0.31 nm-1处，该体系Rashba能量分裂为E0＝1.28 meV，由此可知Rashba系数

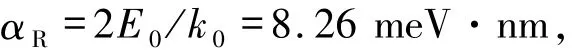
并根据能带结构计算的Rashba系数，可以估算得到对应的DMI为0.18 meV.实验测量多层Co薄膜的电子有效质量约为0.45m0（m0为自由电子质量），石墨烯/三层Co/Ru（0001）多层膜的自旋刚度系数A约为9.5 pJ/m.根据以上的数据可以得到kR＝9.8×10-2nm-1，利用（13）式可以估计出石墨烯/Co的DMI强度约为0.18 meV.这一估计值比前面的计算值稍小，这是由于在估算时仅考虑了费米面附近的一条能带.因此，也就没有考虑到Rashba系数αR的能带依赖特性.然而，它们都有相同的数量级，这再次验证了石墨烯/Co的DMI是由Rashba效应引起的.目前实验上通过测量比较Ru（0001）衬底上生长的Co薄膜在有没有石墨烯覆盖2种情况下的DMI差异，估计出石墨烯/4～6层Co的界面DMI约为

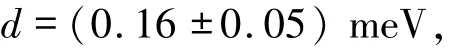
这与上面的计算结果是很接近的.

通过以上的分析，可以看到通过Rashba效应也能诱导出较大的DMI.Rashba效应引起的DMI不再需要非磁层具有强的SOC，从而大大扩展了异质结材料的选择范围.可以预期这种通过Rashba效应来诱导DMI的异质结在提高存储器件读写效率、简化工艺流程、降低制造成本等方面将有巨大的应用前景.

3 基于磁斯格明子的电子学器件

磁斯格明子受到人们的广泛关注不仅仅是因为它独特的受拓扑保护的自旋构型表现出的众多物理性质，如emergent场、拓扑霍尔效应、斯格明子霍尔效应、布朗运动等，更重要的是磁斯格明子具有潜在的应用价值.有着拓扑保护的磁斯格明子是一种天然的信息载体，它显示出易操控、易稳定、尺寸小、驱动速度快等优越的性质，而且从能源消耗的角度来看，磁斯格明子可以被小到102A/cm2的电流驱动，比磁畴的驱动电流小了4个数量级，所以基于磁斯格明子的电子学器件有望满足人们对未来器件非易失、高容量、高速度、低功耗等方面的性能要求.

目前基于磁斯格明子的电子学器件研究领域取得非常多的成果，本文主要介绍以下3个方面：1）磁斯格明子存储器件，2）磁斯格明子逻辑器件，3）磁斯格明子晶体管.图

图6 石墨烯与金属界面的DMI［56］Fig.6 The DMI at graphene-ferromagnet interfaces［56］

3.1 磁斯格明子存储器件随着信息技术的快速发展，人们对器件的性能提出更高的要求，其中寻找具有极佳稳定性的高密度存储方式引领了研究热潮.2008年，Parkin等［71］提出了一种基于磁畴壁（domain wall，DW）的非易失存储方式——赛道存储（racetrack memory，RM），如图7（a）.在这一模型中，磁畴作为存储单元，它们代表了二进制信息中的“0”或“1”.理论上，当利用自旋极化电流驱动畴壁时，速度可达到每秒几百m甚至数km，因而有着良好的读写速度［72］.相比于传统磁存储器件通过移动存储介质在固定位置读取存储介质中磁信息的方式，赛道存储器则是通过携带二进制信息的磁畴壁在赛道上来回运动，从而实现信息的读写存储.更重要的是，这些非易失性的畴壁可以实现信息的复写.因此，赛道存储具有良好的抗干扰性、高读写速度、高存储密度等优势，并有希望取代传统存储方式从而实现大规模存储应用.但是，基于磁畴的赛道存储器因为存在驱动电流阈值过大以及缺陷钉扎效应等急需解决的问题，因而使其发展受到限制.

Fert等［12-13］在2013年首先提出的基于磁斯格明子的赛道存储器，正好弥补了利用DW设计赛道存储器的不足.在基于磁斯格明子的赛道存储器中，二进制基本信息元可通过磁斯格明子的存在为“1”反之为“0”来编译.此外，磁斯格明子赛道存储器中二进制的存储信息“1”和“0”通过读头是否探测到磁斯格明子来记录.典型的磁斯格明子赛道存储器结构如图7（b）所示［73］，其主要结构包括4个部分：供磁斯格明子运动的赛道、在赛道中产生磁斯格明子的写头、探测磁斯格明子的读头，以及驱动磁斯格明子在赛道中运动的电流组件.工作时，首先通过垂直自旋极化电流的注入，在写头中产生磁斯格明子，并在面内电流的驱动下沿着赛道向着读头的方向运动，最终被读头检测到.类似于畴壁赛道存储器中存在多个磁畴来记录信息，磁斯格明子的赛道存储器则引入磁斯格明子链来保证高密度的信息存储，但是磁斯格明子的尺寸小得多，因而在相同器件面积下，斯格明子将能够具有更高的信息存储密度.过密的磁斯格明子链会使得斯格明子间相互作用增强，从而导致磁斯格明子链条重新排列，这会使得信息准确性得不到保证.为此，Zhao等［73］研究了磁斯格明子作为信息载体在赛道存储结构中运动时，磁斯格明子之间的平衡距离.此外，磁斯格明子的驱动电流密度更低，控制灵敏度更高，使得器件功耗大幅降低.更重要的是，磁斯格明子受拓扑保护，将减少信息损耗和波动，这极大地保证了信息存储的鲁棒性.因此，磁斯格明子赛道存储器在高密度存储、低功耗以及信息存储的稳定性方面都具有极大的潜力.

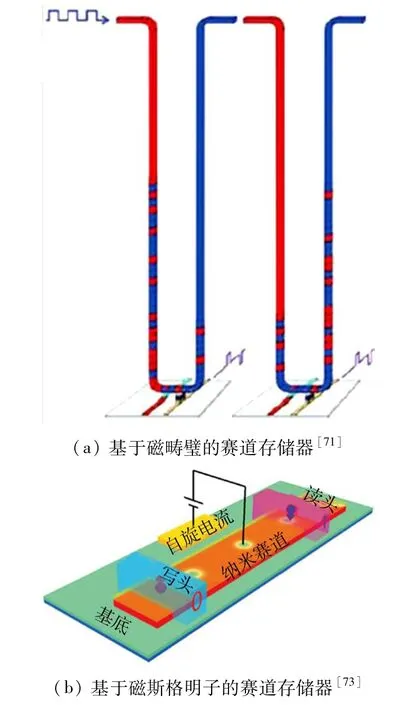
图7 赛道存储器Fig.7 Racetrack memory

在实现磁斯格明子赛道存储器实际应用之前，还需要解决一些问题.首先，若要兼顾信息准确性和高信息存储密度，就得解决磁斯格明子之间由于相互作用带来的影响.为此，人们提出用Y型符合赛道或被刻有凹槽的单一赛道的方案［74］，但是会带来降低存储密度或读写速度等新的问题.其次，需要消除磁斯格明子在被自旋极化电流驱动时产生的磁斯格明子霍尔效应，为此，提出了人工合成反铁磁耦合的双层纳米轨道［75］.此外，也可以通过人工调控赛道存储器纳米带的边界高度、阻尼和垂直磁各向异性来提高边界势垒或势阱，从而能够有效地保证磁斯格明子在赛道中的运动［76-77］.

3.2 斯格明子逻辑器件 除了上述讨论到的基于磁斯格明子的存储器件，最近基于磁斯格明子的逻辑器件也引起了人们极大的研究兴趣.Zhou等［16］研究发现磁畴壁和磁斯格明子之间可相互转换，即提出一种将2条宽窄纳米带链接起来的复合结构，当窄纳米带中的畴壁运动到宽纳米带中会变成磁斯格明子，反之宽纳米带中的磁斯格明子运动到窄纳米带中会变成畴壁，如图8所示.

图8 磁畴壁与斯格明子可逆的相互转换［16］Fig.8 The reversal conversion between magnetic domainwalls and magnetic skyrmions［16］

在此基础上，Zhang等［30］通过Y型轨道实现磁斯格明子复制和融合，如图9所示.在图9（a）中，在输入端中产生的磁斯格明子在电流驱动下穿过较窄轨道的同时转换为一对磁畴壁.在通过Y型交叉点之后，一对磁畴壁分化为2对磁畴壁，最终在输出端输出2个磁斯格明子，从而实现了磁斯格明子的复制，而在图9（b）中显示了磁斯格明子的融合，其形成过程恰好是图9（a）的逆过程.上述描述过程明确展示出了磁斯格明子数Q从2到1的变化.更重要的是，基于磁斯格明子的复制和融合可以实现逻辑“或”门和“与”门操作，如图10所示.该逻辑器件中包含2个输入端和1个输出端，并通过改变连接输入端和输出端的中间部分纳米带的宽度来实现逻辑运算.图10（a）展示了“或”操作，其原理是无论输入端是一个磁斯格明子或同时都有一个磁斯格明子，在通过窄的纳米线后，最终输出端只得到一个完整的磁斯格明子，而如果输入端只有一个磁斯格明子，在通过较宽纳米线后转化为的DW不足以占据整个纳米线，从而形成一个会湮没于纳米线中不完整的DW，由此实现如图10（b）展示的“与”操作.

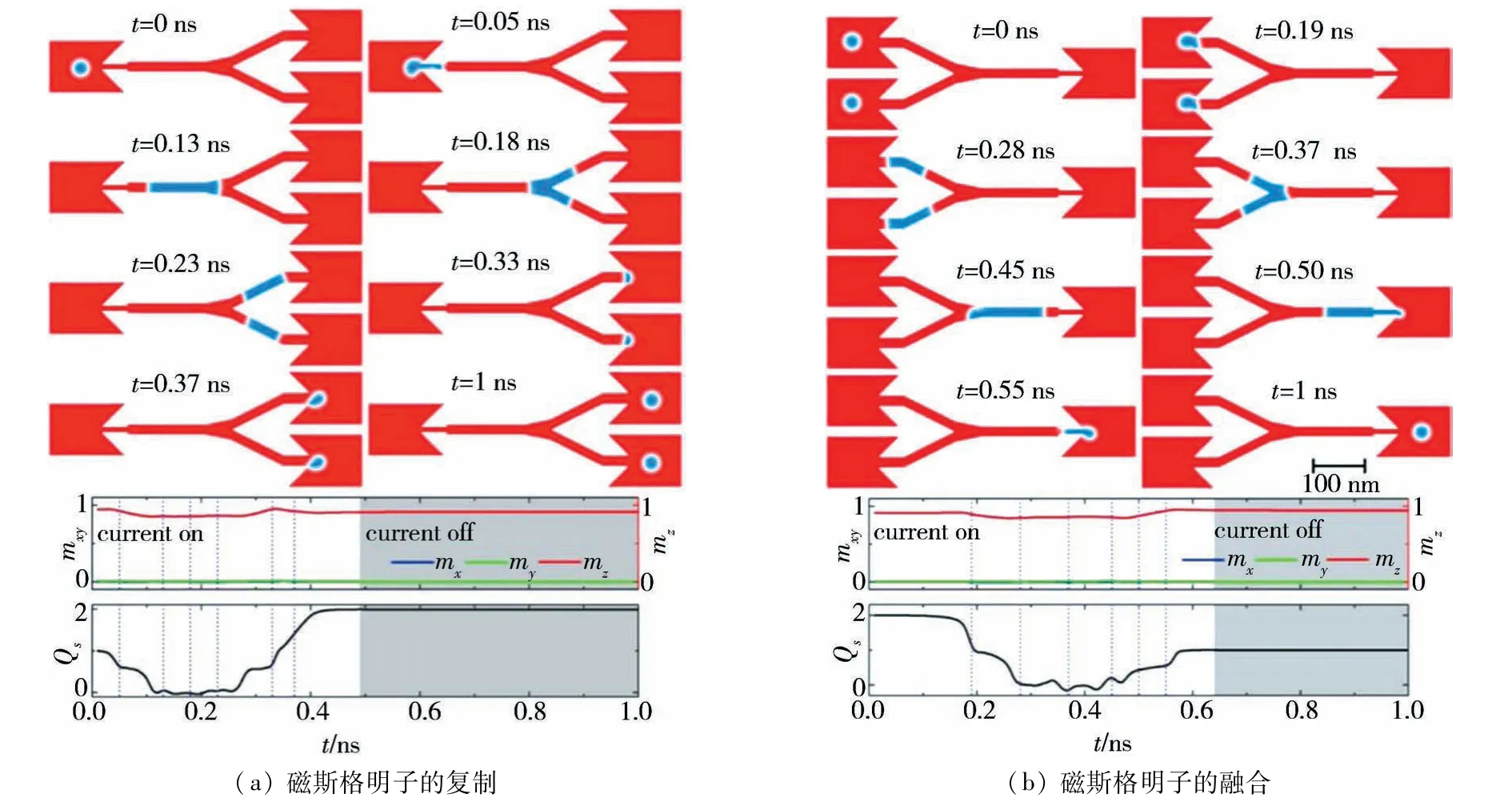
图9 磁斯格明子逻辑器件［30］Fig.9 Magnetic skyrmion logic device［30］

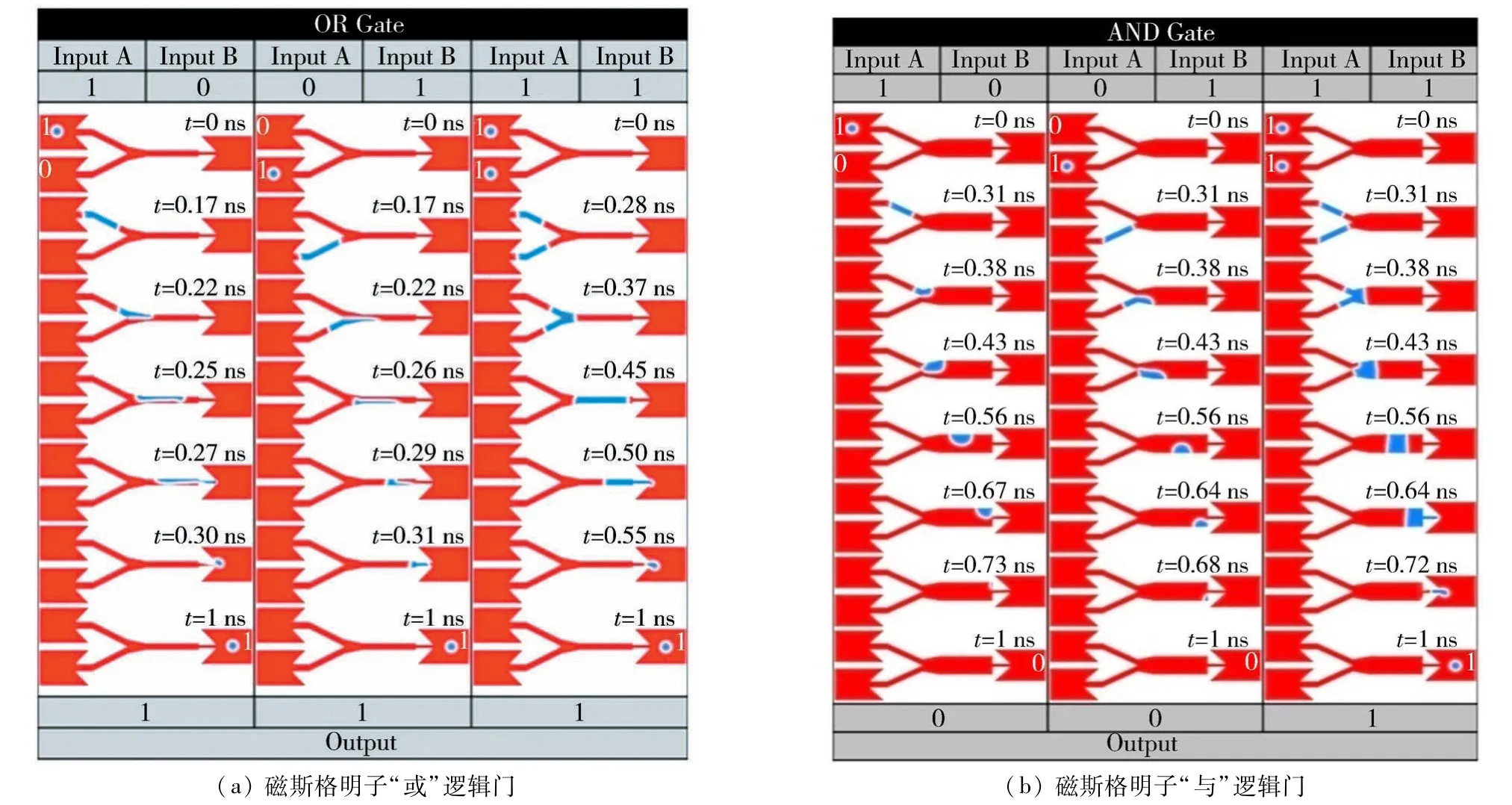
图10 磁斯格明子逻辑操作［30］Fig.10 Illustration of skyrmions logical operation［30］

3.3 磁斯格明子晶体管2015年，Zhang等［29］提出一种基于磁斯格明子的晶体管，如图11左图所示.晶体管左端是源极，它是由置于纳米线上的磁性隧道结组成，并在垂直极化电流的激发下产生磁斯格明子.随后磁斯格明子在纳米线中将被驱动向漏极运动，当运动到磁性隧道结的读头位置时被探测到.在磁性纳米带的中间部分有一个外接电压门电路，如图11右图的阴影部分所示，可以通过外接电压控制局域垂直磁各向异性，进而改变磁斯格明子的运动状态.在电压门区域施加一个正电压时，该区域垂直磁各向异性增大1.1倍，会在电压门的左侧边缘形成一个势垒，在电流的驱动下的磁斯格明子运动到左边势垒处时会被挡住，此时为“OFF”状态.当电压为零时，纳米带中各区域的垂直磁各向异性大小相等，磁斯格明子可以在纳米带上自由运动，此时为“ON”的状态.当施加一个反向电压时，电压门控制区域的垂直磁各向异性减小了1/10，磁斯格明子在向右运动的过程中会被电压门区域右边界处的势垒挡住，此时为“OFF”状态.此外磁斯格明子是否会被限制在电压门区域还取决于其驱动电流密度.因此，会有2种常见的驱动方式：一种方法是源极与漏极之间施加恒定的电流，始终驱动磁斯格明子向漏极运动，并在控制门的作用下选择性地将磁斯格明子限制在源极，或者使其到达漏极，最终实现晶体管的开关功能.另一种方法则是保持控制门区域的垂直磁各向异性不变，形成一个固定的势垒或者势井.在一个较小的电流的驱动下，磁斯格明子会被限制在势垒或势井中.若需要磁斯格明子通过时，加大电流密度使其跨越势垒（井）就可到达漏极.

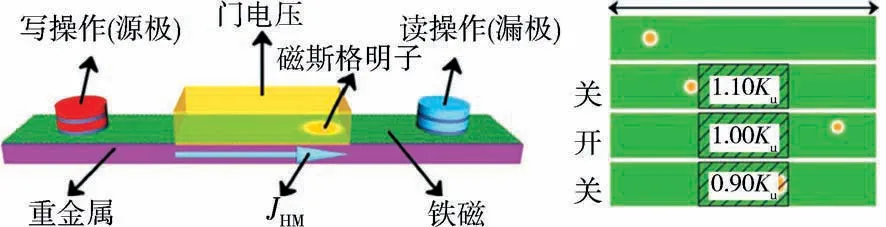
图11 磁斯格明子晶体管［28］Fig.11 Design of magnetic skyrmion transistor［28］

3.4 其他类型的磁斯格明子器件除了上述详细讨论的基于磁斯格明子的器件设计外，再简要介绍其他基于磁斯格明子的器件类型，比如磁斯格明子类脑器件、磁斯格明子二极管等.人工神经网络具有强大的自学能力、联系存储能力、高速寻找优化解的能力，是当前机器学习和相关研究领域的研究热点，并取得了很多突破性的进展.作为生物神经网络的抽象模拟，人工神经网络也是由大量的神经元和突触组成，但这些神经元和突触目前主要以互补氧化物半导体（CMOS）为基本单元.因此，现有的人工神经网络将面临两大主要挑战：1）优化人工神经网络的结构并降低其尺寸；2）降低人工神经网络的能耗.为了解决上述问题，文献［78］首次提出了基于铁磁斯格明子自旋振荡器的人工神经元模型，如图12所示.该设计不仅能适当的缩小神经网络的尺寸，同时还能大大降低体系的能耗.

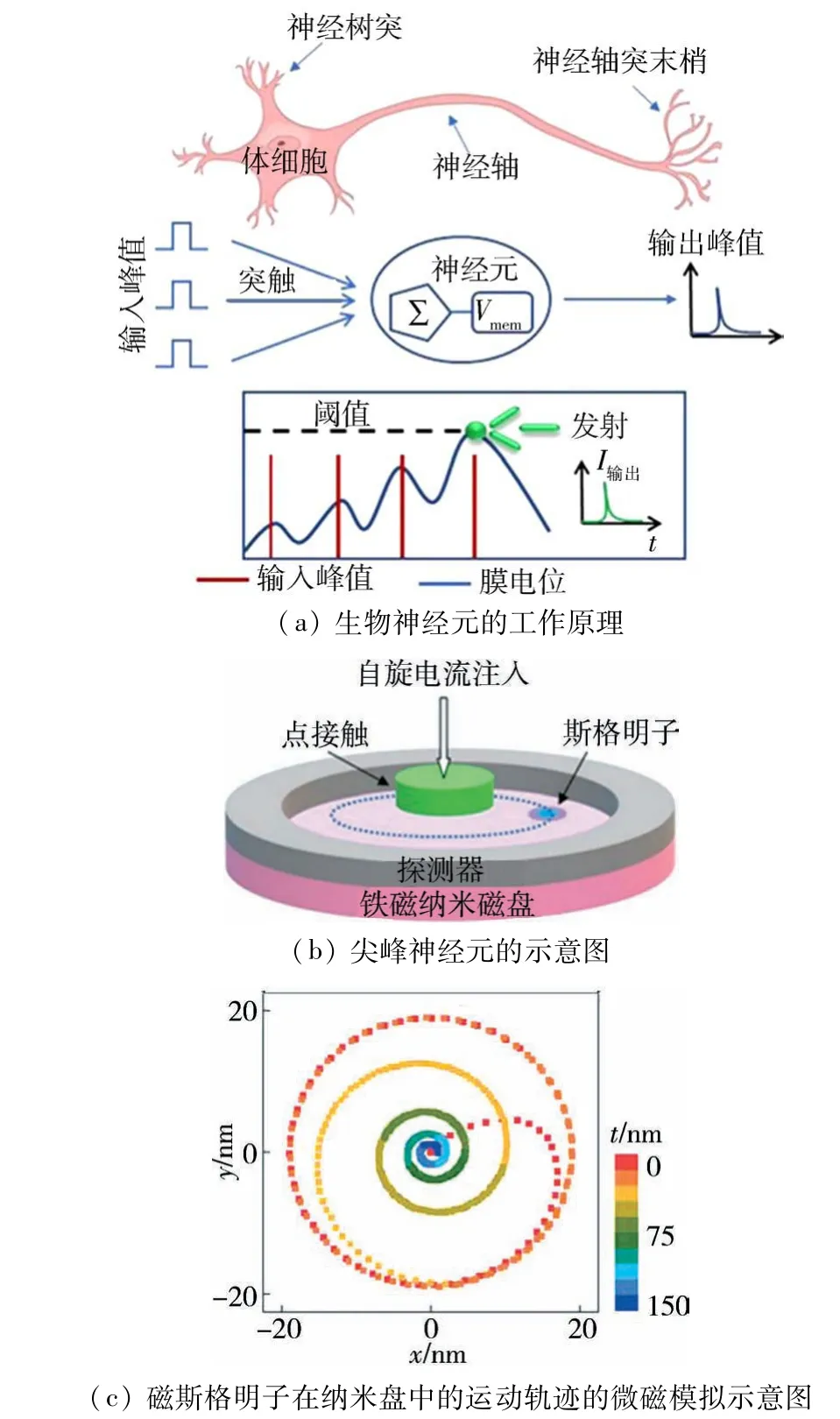
图12 人工神经元模型［78］Fig.12 Demonstration of the structure and function of a biological neuron［78］

此外，Zhao等［79］最近提出了基于铁磁斯格明子的新型二极管，这极大地推动了基于磁斯格明子自旋电子器件应用的发展.这个器件的原理在于电压控制的磁晶各向异性效应（VCMA）使得在边缘和梯形区域产生高垂直磁晶各向异性（PMA），从而达到调控的斯格明子运动的目的.此时高PMA的边缘不仅可以有效避免磁斯格明子在梯形区域中做单向运动过程时被湮灭，还能提高其近11.66%的传输速度，如图13（a）所示.在此基础上，他们进一步提出了一个新型的、可行性高的、类似于PN结的基于磁斯格明子的二极管原型，详见图13（b）.

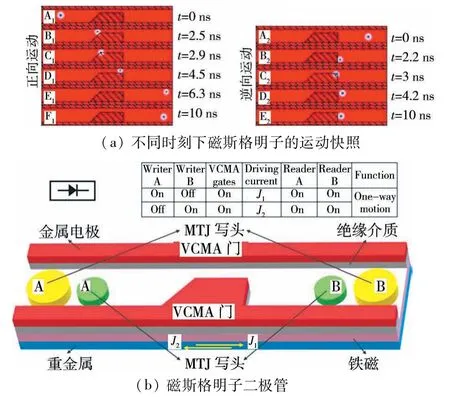
图13 基于磁斯格明子的新型二极管模型［79］Fig.13 Schematic of the skyrmion-based diodemodel［79］

4 磁斯格明子的研究方法

磁斯格明子特殊的拓扑磁结构展示出来的丰富物性以及极具潜力的应用价值引领了研究热潮，人们采取了多种研究手段探究其深刻的物理本质，对应的实验、理论计算和模拟工作也已取得极大地突破.下面将从微磁学模拟、磁斯格明子的产生和湮灭以及实验观测手段简要介绍磁斯格明子的研究方法.

4.1 磁斯格明子的微磁学理论在20世纪60年代，Brown［80］最早提出微磁学（Micromagnetics）概念，旨在更好计算磁体的磁化状态.为此他做出2点假设：1）磁体均匀磁化，外场只改变磁化矢量方向；2）磁化矢量连续分布.一般而言，微磁学包含2种方法：静态方法（Brown静态方程）和动态方法（Langdau-Lifshitz-Gilbert（LLG）方程）.与实验相比，微磁学模拟是种高效的研究手段，它具有很强且可靠的预测能力，这对优化实验有指导意义.另一方面，实验上直接观测磁性材料的磁矩静态分布以及动力学演化具有很大难度，但通过微磁学模拟可以更好地理解磁性材料的结构以及系统在外场刺激下的响应，在一定程度上支撑实验结果.微磁学模拟发展至今，在如计算机强大计算能力的帮助下已经成为当今磁学领域的重要组成部分，对基础物理研究和实际运用都发挥着重要作用.

当系统能量达到最小值或者极小值时，系统会处于稳态或者亚稳态.因此，研究一个磁体的微观机制，其重要内容是考虑该磁体中涉及的相互作用，包括但不限于海森堡交换相互作用、偶极相互作用、DMI等.系统中的总磁能定义为

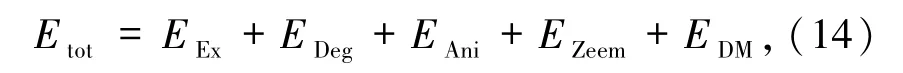
其中，EEx代表交换能，EDeg代表退磁能，EAni代表各向异性能，EZeem代表外场能，EDM代表DMI能.当系统总磁能最低时，则意味着系统处于稳定状态.

正如上述列举的微磁学方法，系统的静态磁化强度分布通过Brown方程

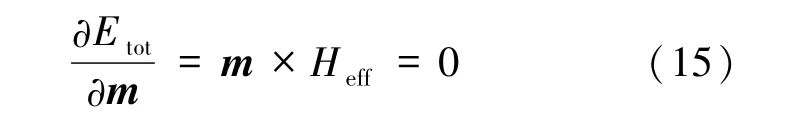
给出，其中Heff为总的有效场，m为单位磁化强度.而解决动态微磁学问题，则可以用LLG方程［81］

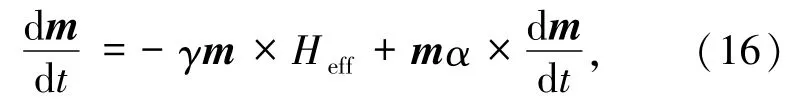
其中，γ为旋磁比，α为吉尔伯特阻尼因子.

若考虑在赛道存储器中磁斯格明子的输运行为，可以通过面内和垂直电流2种方式驱动磁斯格明子.电流驱动的磁斯格明子运动可以用Thiele方程［82］

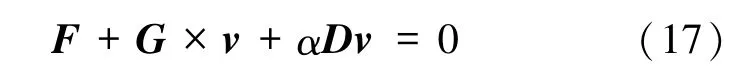
来描述，其中，F是磁斯格明子受到赛道的作用力，G为回旋矢量，其符号取决于磁斯格明子数的正负，v是磁斯格明子的运动速度，D是耗散矩阵.对于面内电流驱动的情况，Thiele方程［13］可写成

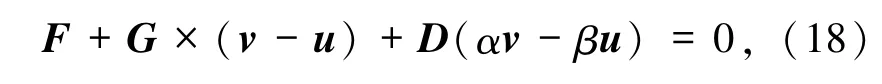
其中，v为自旋极化电流的大小正速度，比于电流密度，β为非绝热因子.相反，在垂直电流的作用下，磁斯格明子的运动方程则为

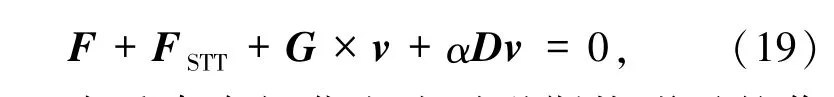
其中FSTT为垂直自极化电流对磁斯格明子的作用力.

4.2 磁斯格明子的产生和湮灭方式 在实现磁斯格明子实用化的发展过程中，首要解决的关键问题是如何利用高效、快速、低能耗的手段产生和湮灭单个磁斯格明子.磁斯格明子是受拓扑保护的准粒子，而自旋螺旋态或铁磁态都是拓扑平庸态.对于具有不同拓扑结构的态之间，不可能通过连续形变相互转换，即在这些态之间存在着一个有限的能量势垒.因此，如果要实现拓扑平庸态到磁斯格明子的转换，必须要克服它们之间的拓扑势垒［13］.

目前实验上能实现磁斯格明子成核的途径很多，比如人们通过外加磁场改变系统的整体能量，从而获得稳定存在的磁斯格明子，且探讨了磁场作用下单轴磁各向异性等因素对磁斯格明子稳定性的影响［83-84］，而Romming等［85-86］进一步地研究了单个磁斯格明子的尺寸和形状对外磁场的依赖性.当外加磁场与系统温度处于某一区间（“A”phase）时，在B20结构材料体系（MnSi、FeGe等）中磁斯格明子会作为系统自旋排列的能量基态出现，并整齐排列成斯格明子阵列.最早观察到的磁斯格明子即是采用这种方式在MnSi块材中激发得到［9］，如图1（a）所示.若将MnSi材料做成具有菱形截面的纳米线，可以通过磁场控制在其截面产生或湮没磁斯格明子［87］.进一步通过对FeGe的研究发现，这一方法得到的斯格明子会首先在材料的缺陷［88］或是边缘［14，89］处成核，如图14（a）和（b）所示.此外，在非对称的多层膜体系中产生了室温下单个磁斯格明子［22-24］.这种多层膜结构为铁磁层和重金属层的交替重复堆垛，使得有效磁体积增大，可以大大提高体系的热稳定性，并且该体系只需要几十毫特斯拉产生磁斯格明子，从而大大降低了能耗.

直接利用自旋转移力矩来产生和湮灭磁斯格明子是在自旋电子学的背景下比较常见的实验方法.此时有2种不同的作用方式，即面内电流主导（current flowing in the film plane，CIP）［90］和垂直面电流主导（current flowing perpendicularto the film plane，CPP）［91］.CIP是平行于铁磁层面内注入自旋极化电流，对局域磁矩产生面内自旋转移力矩，从而产生磁斯格明子；CPP则是垂直于铁磁层注入自旋极化电流，从而产生磁斯格明子.为实现这些操作，对于CIP结构可以人工设计缺陷［92］，利用特殊设计的边界条件（如图15（a））或者是利用纳米条带带宽非均匀性来实现磁斯格明子的产生（如图15（b）和（c））.而对于CPP结构可以利用自旋阀（如图15（d））或者磁性隧道结［13］.这类结构中有一层额外的铁磁薄膜作为自旋极化层，通过垂直施加电流最终在磁斯格明子材料薄膜中注入一个自旋极化电流，从而产生磁斯格明子.另外，还有一种方法是利用自旋极化扫描隧道显微镜（spin-polarized scanning tunnelingmicroscopy，SP-STM）向斯格明子材料薄膜中注入自旋极化电流，从而产生磁斯格明子［85］，如图15（e）.

图14 样品缺陷及形状对磁斯格明子成核的影响Fig.14 The influence of sample defects and shape on the creation of magnetic skyrmion

除上述介绍的途径之外，还有一些其他具有潜力的实验手段，比如激光是凝聚态物理中一种常用的实验方式.因此，Finazzi等［93］对斯格明子磁性薄膜施加激光脉冲实现了斯格明子的产生和湮灭，如图16（a）所示.2014年，文献［94］证明了给手性磁体或偶极磁体局部加热可以激发出磁斯格明子，如图16（b）所示.再比如在特殊设计的十字结构中，用了磁斯格明子/非磁斯格明子材料异质结构，通过自旋波的诱导，从而可以实现斯格明子的非局域产生和湮灭［95］，如图16（c）所示.另外，在多铁斯格明子材料中，还可以通过施加局部电场利用其多铁的性质来产生和湮灭斯格明子［96］，如图16（d）.以上这些实验或理论研究成果为磁斯格明子的发展提供给了丰富的思路.意图［17］

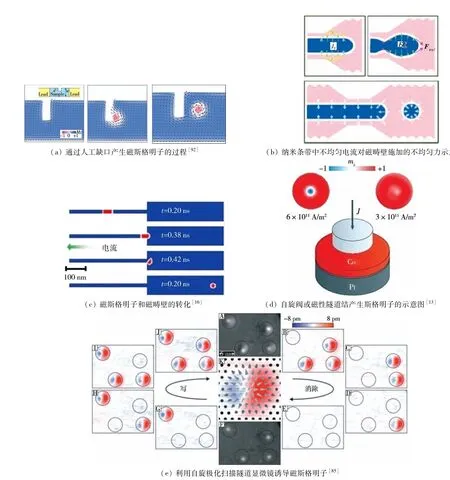
图15 磁斯格明子的激发Fig.15 Creation of magntic skyrmions

4.3 磁斯格明子的实验观测技术2009年，Mühlbauer等［9］首次在实验上观测到了MnSi块材中磁斯格明子在倒空间中所形成的衍射斑点，并给出了该体系下磁斯格明子存在的条件相图，这对磁斯格明子的研究具有深远的意义，其中他们使用了先进的中子散射技术.该技术利用具有不带电、有磁矩、穿透力强等特点的中子与测试样品发生相互作用，从而实现研究物质磁性和磁结构，是物质静态结构和微观动力学行为的一种先进实验手段.但是，中子散射仅仅能探测到斯格明子的存在，并不能给出其实空间的磁矩分布.2013年，Nagaosa团队［34］利用洛伦兹透射电子显微镜（Lorentztransmission electron microscopy，LTEM）解决了这一问题.LTEM是一种研究磁斯格明子自旋结构的强有力技术，被广泛地应用于B20结构样品中斯格明子的观测.它具有2种工作模式：1）普通透射电子显微镜加LTEM.在普通透射电镜工作模式下，物镜会在样品附近产生高达2～3个特斯拉的磁场，从而直接饱和磁化一般的磁性样品，而采用一个远离样品的LTEM代替物镜的成像功能，从而使得样品区域的磁场强度大幅度降低（通常200～300 Oe）.2）另一种是特制的LTEM.此时透射电镜的极靴及物镜被特殊设计和加工，使得样品处磁场可以降到10 Oe以下，十分有利于磁结构的观察.

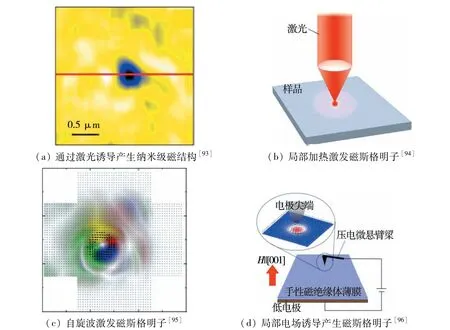
图16 其他产生磁斯格明子的途径Fig.16 Creation of magntic skyrmions in other ways

利用高分辨率的X射线进行实空间观测磁斯格明子也是一种强有力的观测手段.2016年，文献［24］利用扫描X射线透射显微镜（scanning X ray transmission microscopy，STXM）发现了室温下（Ir/Co/Pt）10多层膜中稳定存在的斯格明子.同年，Boulle等［22］也通过X射线磁圆二色光电子显微镜（photoemission electron microscopy combined with X ray magnetic circular dichroism，XMCDPEEM）观测到了室温下Pt/Co/MgO结构中的斯格明子.虽然利用X射线可以取得足够精确的分辨率，但是由于实验技术本身过于复杂性，因而操作起来比较困难.近年来，磁力显微镜（magnetic force microscopy，MFM）也被广泛地应用于观测磁斯格明子静态结构分布［35］及其动态演化过程［97］.而对于大尺寸的磁斯格明子（微米级）来说，极性磁光克尔显微镜（polar magneto-optical Kerr effect（MOKE）microscope）则是更方便的实验手段.实际上，第一个在室温下观测到的斯格明子，即是采用的这种相对简单易行的方法［18］.

除此之外，还有很多具有实用潜力的实验手段，比如自旋极化扫描隧道显微镜（SPSTM）［15，85］、低能电子显微镜/光发射电子显微镜（LEEM/PEEM）［10］、自旋极化低 能电子显微镜（SP-LEEM）［98］等.针对磁性薄膜样品的磁畴结构特点，SP-STM得到样品表面的形貌信息，具有原子级别实空间分辨率的优点.因此，可以用于磁斯格明子的观测.磁性材料费米面附近，电子的局域态密度与其自旋方向有关，其不对称性会导致STM的针尖与样品表面之间形成极化和非极化的隧穿电流.极化电流中包含了样品表面与自旋相关的磁信息，而从非极化电流中可得到样品表面的形貌信息.LEEM/PEEM是磁畴结构观察的重要实验手段，其中LEEM技术是利用被激发出来的低能电子（小于30 eV）的弹性背散射对样品表面进行成像；而PEEM的工作原理是基于爱因斯坦光电效应，利用被激发出来的二次电子对样品表面进行成像.LEEM与PEEM通常为同一台电镜中的2种成像模式，成像方式便于切换，给表面成像带来了极大的便利.

5 总结

受拓扑保护的斯格明子作为信息载体极大地简化了传统器件中复杂的操作方式，且使得器件存储密度以及性能得到相应提升的同时，其热稳定性和磁稳定性也都将提升.

回顾了磁斯格明子的发展过程和独特的拓扑性质，探讨了关于磁斯格明子的产生和湮灭方式、研究手段以及基于磁斯格明子的自旋电子学器件等的研究进展.详细介绍了DMI的形成机制，着重从第一性原理计算的角度研究界面DMI的性质.第一性原理计算不仅可给出界面DMI的大小、手性以及等效的微磁模拟DMI系数，还可以进一步给出DMI的空间分布和能量来源，这为理解DMI的形成机制提供了一个清晰的物理图像.对比分析了Fert-Levy型DMI和Rashba效应引起的DMI的性质，发现这2种DMI虽然都属于界面效应，但它们的主要贡献来源是不同的.通过实验观测、微磁模拟等手段，人们对磁斯格明子的物理本质有了更深刻的认识，尽管如此，斯格明子电子学器件离实际应用尚存在一些亟待解决的基础科学及技术问题，需要在材料结构选择、操控手段及工艺技术等方面开展更深入的研究.