条带开采煤柱支承压力与塑性区分布规律研究

谷拴成，杨超凡，王 盼，牛宏新

(西安科技大学 建筑与土木工程学院，陕西 西安 710054)

煤炭作为我国最重要的基础能源与工业原料，对国民经济发展起着举足轻重的作用。目前，国内相当一部分煤炭资源埋藏在众多的地面建筑物下、铁路下与水体下(简称“三下”)。据不完全统计，“三下”压煤量在137.9亿t左右[1]，“三下”煤体的安全高效开采是实现矿井可持续发展的关键。条带开采由于技术成熟、方法简单，在“三下”采煤中得到了广泛应用。在条带开采中，现阶段主要通过留设煤柱支承上覆岩层以达到减少覆岩沉陷，控制地表移动和变形，保护采准工作面的目的[2-3]。煤柱设计则主要分为3个步骤进行，即首先计算煤柱受力，明确煤柱支承压力分布情况；其次是在明确煤柱支承压力分布情况的基础上，对煤柱塑性区范围进行确定；最后对煤柱宽度的最终尺寸进行设计。关于煤柱支承压力分布及塑性区分布这一课题，国内外众多学者开展了广泛的研究工作[4-7]。WILSON A H在1972提出了两区约束理论[8]，取埋深H处的煤柱上覆岩土体平均重度为γ，引入应力增大系数K后，威尔逊认为煤柱上的最大支承压力为KγH，依据英国地区煤矿开采经验，建议应力增大系数取为4；基于两区约束理论，ZHANG L Y等[9]利用FLAC3D数值模拟软件研究了煤柱弹塑界面应力增大系数K的变化规律及煤柱稳定性；张科学等[10]对窄煤柱采空区侧向支承应力分布规律进行了数值模拟研究；于远祥等[11]将煤柱支承压力进行简化，采用弹性力学方法对煤柱极限平衡区宽度进行了研究；杨俊哲等[12]采用FLAC3D数值模拟软件对神东保德煤矿81505综放工作面不同沿空煤柱宽度下的围岩应力分布、变形及塑性区的分布规律进行了研究，对比得到了沿空煤柱和巷间煤柱的合理尺寸；吴立新等[13]在研究影响煤柱塑性区宽度的因素时，所建立的煤柱支承压力模型考虑到了切向应力的影响，但部分参数取值仍依赖于现场经验。现阶段对煤柱支承压力分布情况的研究，对现场经验或数值模拟依赖度较高[14-19]，理论研究有待进一步完善。笔者以地下工程中普遍存在的成拱效应作为切入点，通过建立采空区上覆岩土体自重荷载经拱向煤柱传递的传力拱模型，对煤柱支承压力分布情况进行研究，在明确煤柱支承压力分布情况后，结合玉华煤矿生产实际，模拟研究不同工作面埋深、不同采空区宽度下煤柱塑性区分布规律，得出在依据本文给出的煤柱支承压力计算方法模拟计算出的煤柱最大塑性区宽度。最后，根据玉华煤矿现场监测结果，对该计算方法的合理性进行验证。

1 采空区传力拱模型建立

1.1 基本假定

地下岩土体成拱效应，是指岩土体开挖后未垮落岩土体由于其具有抗压性能好、抗拉能力差的特点，在外荷载作用下，岩土体进行自我优化调整的成拱现象[20-21]。因此，在地下采煤活动中，随着工作面的推进，采空区上方部分煤岩体将垮落，并由于碎胀性最终填充采空区，而未垮落煤岩体将在采空区上方形成传力拱。该传力拱将地表至拱顶范围内的煤岩体自重荷载部分传递至煤柱。结合现场生产中观测的结果，以及岩土工程中广泛使用的普氏拱理论，将采空区上方的拱简化为水平拱，认为其处于平面应变状态。提出以下假定：

1)采空区上部煤岩体坍塌后所形成的拱只能承受压应力，不能承受拉应力；

2)考虑到拱内垮落煤岩体的碎胀性，垮落后煤岩体将完全填充拱内空间，且具有一定的承载能力；

3)为了保证拱传力的稳定性，假定拱脚坐落于煤柱上部坚硬顶板上；

4)拱脚处水平推力T与竖向压力V、煤岩体坚固性系数f的关系，与普氏拱理论中的相关假定一致[22]，即 2T=fV。

由以上假定，建立如图1所示传力拱物理模型。

图1 传力拱物理模型

图1中：b为传力拱拱高，m；M为工作面采高，亦即煤柱高度，m；a为采空区宽度的一半，m;Q为每米采空区上覆岩土体自重，N/m。

1.2 拱轴方程求解

根据传力拱物理模型，忽略拱高范围内作用于拱上的煤岩体自重，由假定2)可知，采空区上覆煤岩体自重荷载由拱与拱内垮落煤岩体共同承担，荷载分配关系可根据King与WILSON A H的研究确定，拱承担的荷载p可近似取为Q/5，据此将图1所示的物理模型简化为图2所示的传力拱力学模型。考虑到结构对称性，将左半部分拱的水平推力用T′代替，选取右半部分拱结构进行分析。

图2 传力拱力学模型

图2中：p为上覆岩层自重荷载中由拱承担的部分，N/m；T′为左半部分拱作用于拱顶的水平推力，N；R为拱支座承受的支座反力，N；T为R的水平分量,N；V为R的竖直分量，N；α为R与水平方向的夹角,(°)；d为煤柱顶部的拱传力影响范围，m。

根据静力平衡方程可得：

(1)

由于所有外力对拱上任意一点(x,y)取矩结果为0，因此可得：

(2)

根据假定4)和式(1)，推导可得：

(3)

式中:Rc为煤的单轴抗压强度，MPa；f为煤体坚固性系数。

2 煤柱支承压力计算

在确定出传力拱方程、拱高及拱脚反力后，进一步结合Mohr-Coulomb理论对煤柱受力进行分析。首先建立如图3所示力学模型。

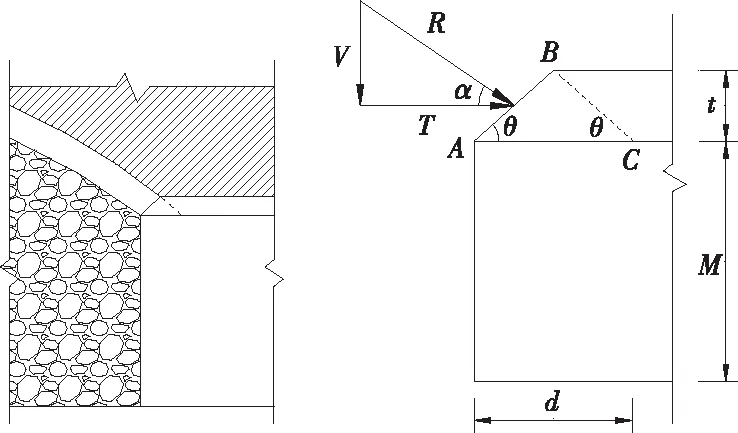
图3 传力拱—煤柱交界处细部物理力学模型

图3中：θ为剪切破裂面与煤柱顶部平面夹角，(°)；t为支承传力拱拱脚的岩层厚度，m。

当拱脚处于极限状态时，煤柱上部支承拱脚的岩层中将形成AB剪切破裂面，拱上部边界在岩层的延伸线BC与剪切破裂面AB形成传递拱脚荷载的刚性三角形ABC，拱承担的采空区上覆岩土体自重通过拱脚，由刚性三角形ABC弥散至煤柱顶部宽度d范围内，近似取ABC为等腰三角形，这样近似处理便于计算，且对计算结果影响不大。

在AB剪切破裂面上，由Mohr-Coulomb强度准则，可建立方程：

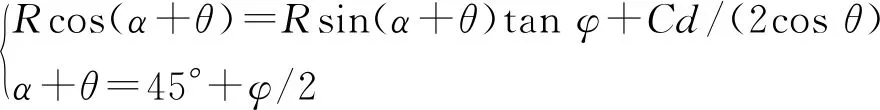
(4)

式中：φ为煤体内摩擦角，(°)；C为煤体黏聚力，MPa。

若已知煤体的C、φ，以及采空区宽度2a与工作面埋深H，联立式(1)、式(3)、式(4)可解出煤柱顶部拱传力影响范围d,以及拱脚剪切破裂面与煤柱顶面水平方向的夹角α，可得煤柱支承压力计算公式(5)，其分布情况如图4所示。

(5)

式中:σa、σb、σc为煤柱顶部正应力，Pa；γ为覆岩平均重度，kN/m3;τa为煤柱顶面切应力，Pa。

(a)传统理论 (b)本文理论

以两区约束理论为代表的传统煤柱支承压力分布(见图4(a))理论计算的可行性较低，且未考虑作用于煤柱顶面切向应力。与传统理论相比，依据传力拱理论给出的煤柱支承压力分布(见图4(b))，考虑到了切向应力对煤柱的影响，在煤柱支承压力计算方面可行性较高。

3 煤柱塑性区宽度分布规律模拟研究

3.1 参数选取

铜川市焦坪矿区玉华煤矿2410工作面上覆岩土体平均重度为20 kN/m3，工作面开采后形成的采空区宽度为240 m，采高为6 m。实测煤体的物理力学参数见表1。在进行数值模拟时，选取不同工作面埋深H(400～600 m)、不同采空区宽度2a(100～260 m)，对煤柱塑性区分布进行研究。

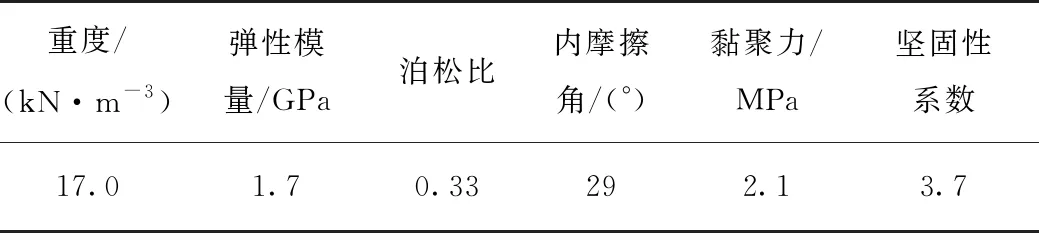
表1 煤体物理力学参数

在模拟计算前，先对煤柱支承压力分布情况进行确定，结合玉华煤矿2410工作面现场资料，采用式(1)、式(3)、式(4)对不同工作面埋深H(400～600 m)、不同采空区宽度2a(100～260 m)下煤柱顶部拱传力影响范围d进行计算，结果见表2。

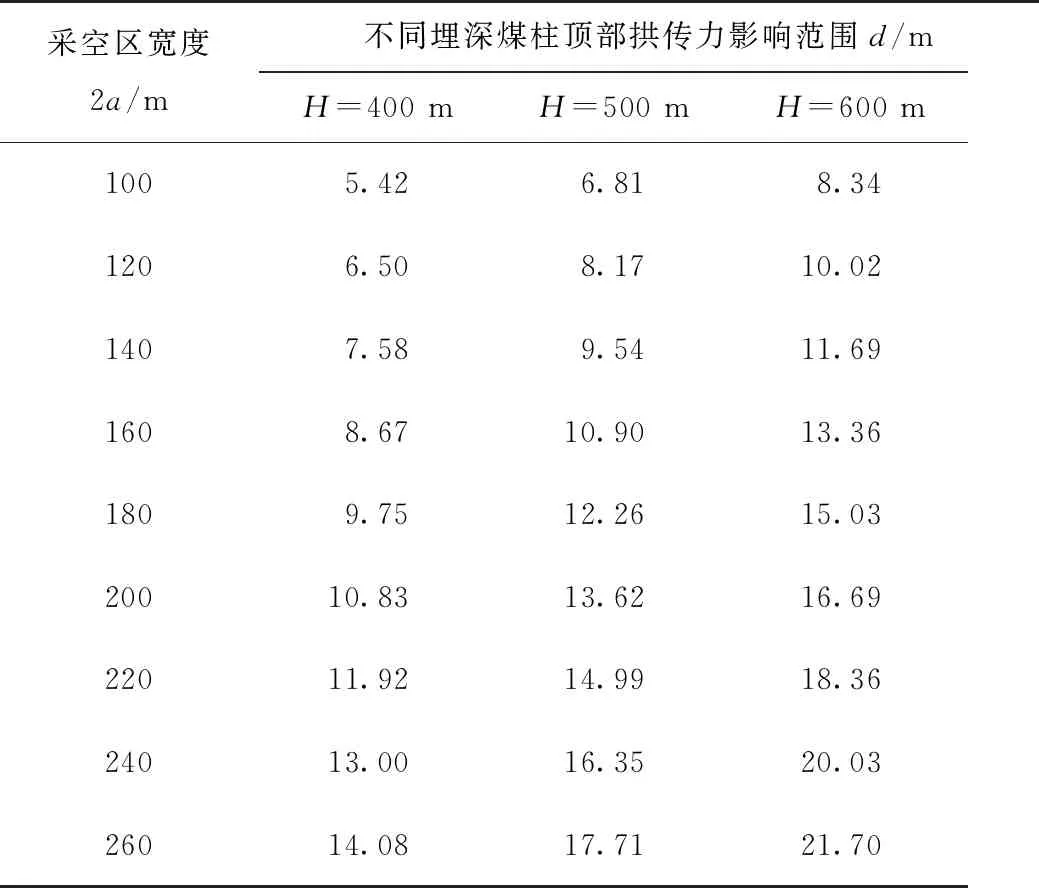
表2 煤柱顶部拱传力影响范围计算结果

联立式(1)、式(3)、式(4)计算出的煤柱顶部拱传力影响范围d，是确保传力拱能形成的基础，若煤柱留设宽度小于d，则无法形成稳定传力的拱。因此，d为留设煤柱宽度的最小尺寸。

3.2 模型建立与求解

依据表2和式(5)计算出的煤柱顶部拱传力影响范围与煤柱支承压力，进一步采用ANSYS15.0有限元分析软件进行模拟计算，通过数值模拟，对煤柱塑性区分布规律进行研究。

在不同工作面埋深、不同采空区宽度的影响下，共进行了27组模拟，以与玉华煤矿生产条件相同的一组(H=600 m,2a=240 m)为例，对建模过程进行详细说明。

建模时采用8节点plane42单元，并在划分网格时对临近采空区侧煤柱进行局部加密处理。建立如图5所示共计13 000个节点的有限元模型。进一步通过表面效应单元surf154对煤柱施加支承压力。

图5 煤柱有限元分析模型

模拟求解过程中，考虑到几何非线性及煤体材料非线性的影响，启用大变形选项。为了保证模拟计算结果的收敛性，将每个荷载步中的荷载子步设置为500步，采用力与位移协同收敛准则进行模拟计算。

3.3 模拟结果分析

与玉华煤矿地质生产等条件相同的一组(H=600 m,2a=240 m)模拟结果见图6，以此为例，对煤柱塑性区分布规律进行说明。

(a)切应力分布云图 (b)等效塑性应变分布云图

由图6可知，在煤柱顶部承受有较大的切应力，且在距离采空区侧煤帮d/2至d处，切应力值达到最大，为36.7 MPa。煤柱塑性区宽度在煤柱不同高度处并不相等，在煤柱中间处煤柱的塑性区宽度最大，向煤柱顶、底处塑性区宽度逐渐递减，且最大塑性区宽度为2.07 m。数值模拟所揭示的煤柱塑性区分布规律与在玉华煤矿现场所得规律一致。

其余26组条件下模拟计算的煤柱最大塑性区宽度见表3。

表3 煤柱最大塑性区宽度模拟计算结果

由表3可见，当工作面埋深H一定时，随着采空区宽度2a的增加，临近采空区侧煤柱最大塑性区范围不断扩大；采空区宽度2a一定时，随着工作面埋深H的增加，临近采空区侧煤柱最大塑性区范围也在不断扩大。最大塑性区宽度随采空区宽度变化曲线如图7所示。

图7 最大塑性区宽度随采空区宽度的变化曲线

4 现场监测

依据煤柱支承压力计算方法，结合玉华煤矿生产条件(H=600 m，2a=240 m)，模拟计算出的煤柱最大塑性区宽度为2.07 m。对比现场监测与模拟计算结果，对所提出的煤柱支承压力计算方法的合理性进行验证。

4.1 测点布置与数据采集

监测站布置在玉华煤矿2410工作面回风巷道。在煤柱侧壁共安装3个钻孔应力计，安装位置分别距离煤壁深1、2、3 m。2410工作面回风巷道煤柱应力计安装后，在超前工作面90 m至工作面推进到监测站的实测煤柱应力曲线如图8所示。

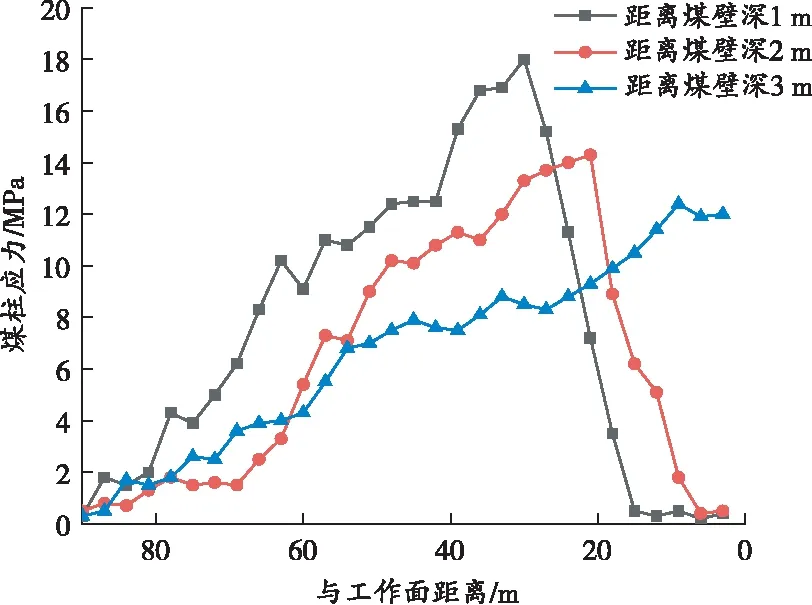
图8 实测煤柱应力变化曲线

在监测站内煤壁中部位置钻进深5 m的窥视孔，通过窥视仪对煤柱内部情况进行观测，评估煤柱内部破坏情况。窥视结果如图9所示。

(a)距离煤壁深3.0 m (b)距离煤壁深2.5 m

(c)距离煤壁深2.0 m (d)距离煤壁深1.5 m

4.2 监测数据分析

在回采过程中，随着采空区的形成，距离煤壁1.0 m和2.0 m深处的应力值呈现先增大后减小的趋势，在回采工作面靠近监测站30.0 m时，距离煤壁1.0 m处的煤柱应力开始下降，说明此时1.0 m处的煤柱发生了破坏；在回采工作面靠近监测站21.0 m时,距离煤壁2.0 m处的煤柱应力开始下降，说明此时2.0 m处的煤柱发生了破坏；距离煤壁3.0 m处的应力计读数随着工作面的推进在不断增大，随后保持平稳，表明距离煤壁3.0 m深处的煤体具有足够的承载能力，未发生破坏。据此可判定在采空区形成后，煤柱最大塑性区宽度在2.0～3.0 m。

进一步结合窥视结果，发现在距离煤壁深1.5 m和2.0 m处，窥视孔孔壁破碎严重，表明距离煤壁此深度范围内的煤体发生了塑性破坏；在距离煤壁深2.5 m和3.0 m处，窥视孔孔壁较为光滑，没有发生塑性破坏，由此可进一步确定煤柱最大塑性区宽度在2.0～2.5 m内。

实测结果表明，煤柱最大塑性区宽度稳定在2.0～2.5 m内。与依据本文煤柱支承压力计算方法模拟计算的2.07 m一致，验证了该计算方法的合理性。

5 结论

1) 依据岩土工程成拱效应，建立了煤矿开采过程中采空区上覆煤岩体传力拱模型，并推导出采空区上方形成的传力拱的拱轴方程。

2) 依据传力拱模型求解结果，建立了煤柱受力模型，对煤柱进行极限平衡分析，给出了在考虑采空区上覆煤岩体的成拱效应下的煤柱支承压力计算方法。

3) 依据本文煤柱支承压力计算方法，结合ANSYS15.0进行模拟计算，结果表明：塑性区宽度在煤柱中间最宽，并向煤柱顶、底递减；煤柱顶面受到较大的切向应力；煤柱的最大塑性区宽度随着工作面埋深及采空区宽度的增加而增大。

4) 将玉华煤矿2410工作面回风巷道的煤柱受力，以及煤柱内部破碎程度监测结果，与模拟计算结果对比，发现煤柱最大塑性区宽度监测值与依据本文计算方法模拟计算出的数值相吻合，验证了采用本文煤柱支承压力计算方法的合理性。