钻井液滤失对煤岩井壁稳定性的影响

张 毅，陈 东，张 慧，刘蒙蒙，刘 富，魏 凯

（1.中联煤层气国家工程研究中心有限责任公司，北京100095；2.中石油煤层气有限责任公司，北京100095；3.新疆煤田地质局一五六煤田地质勘探队，新疆 乌鲁木齐830009；4.长江大学 石油工程学院，湖北 武汉430100）

在钻井施工过程中，由于井壁失去支撑使围岩应力重新分布，产生的应力集中很容易导致井壁失稳，为了维持井壁稳定，通常利用钻井液的静液柱压力支撑井壁[1-2]，但对于煤岩地层来说，由于割理、裂隙等缺陷发育[3-4]，当提高钻井液密度时，若钻井液封堵性能不佳，钻井液很容易侵入井眼周围的煤岩，从而改变井眼围岩的地层孔隙压力，继而改变围岩应力场，影响井壁稳定性[5-7]。

国内外学者Thomas Gentzis 等，通过实验测试了含有FLC 2000TM 和Q-stop 添加剂的聚合物钻井液，该体系能够快速形成泥饼，防止钻井液滤失，使用该钻井液的阿尔伯特两口煤层气水平井施工时未发生井壁失稳，表明钻井液滤失对煤岩井壁稳定有影响[8]；屈平和申瑞臣指出，裂纹的失稳扩展是导致节理煤岩失稳的主因，孔隙压力会改变裂纹的受力状态，影响裂纹的扩展[9]；Milad A kbarpour 通过数值模拟表明，地应力、孔隙压力、岩石强度、井内压力和井眼轨迹等参数是影响井壁稳定的关键因素[10]。可以看出，孔隙压力对于井壁稳定具有显著影响，但通常将孔隙压力作为定值，未考虑钻井液滤失时导致的孔隙压力随与井眼距离的变化，也未考虑钻井液渗流场和煤岩应力场间的耦合关系，对于指导井壁稳定性评价和钻井方案设计具有一定局限性。

综合考虑钻井液滤失对煤岩的物理作用[11]，建立了考虑钻井液与煤岩相互合作用的井壁稳定性评价的流固耦合模型，通过数值方法对模型进行了求解，对比分析了钻井液滤失对井壁围岩应力场和渗流场的影响，并通过工程实例验证了钻井液滤失对煤岩稳定性的影响，为煤岩井壁稳定性评价提供了方法。

1 钻井液在煤岩中滤失时的流固耦合模型

煤岩具有割理、孔隙等多孔特性[12]，通常将煤岩骨架与割理、孔隙中流体间的相互作用称为“流固耦合”作用[13]。因此，建立应力-渗流的耦合模型，是分析钻井液滤失对煤岩井壁稳定性的基础。煤岩的多孔介质模型示意图如图1，流固耦合模型满足以下假设[14]：①煤岩为各向同性均质模型；②井眼横截面是圆形的；③地层无限大，拟分析二维平面应变问题。

根据多孔介质的有效应力原理[15]，煤岩有效应力可表示为：

式中：σ′为煤岩有效应力张量，Pa；σ 为煤岩应力张量，Pa；p 为煤岩孔隙压力，Pa；Bi为Biot 系数，无量纲；I 为单位张量。

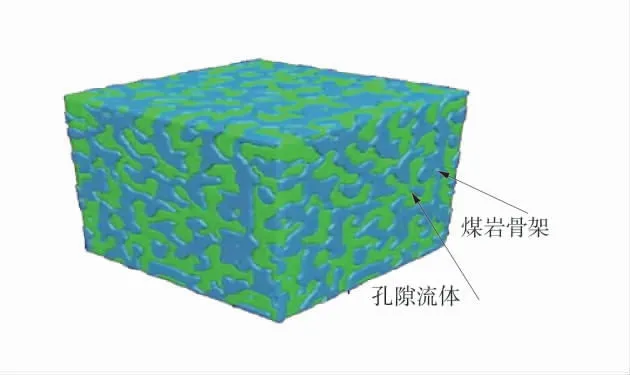
图1 多孔介质模型示意图Fig.1 Schematic diagram of porous media model

另外，煤岩满足静力平衡关系：

式中：F 为体积力，N；▽为哈密顿算子。

当钻井液侵入煤岩孔隙时，孔隙压力p 与井眼的距离有关，因此，若只考虑重力场，当钻井液滤失时煤岩骨架应力与孔隙压力间满足以下关系：

式中：ρ 为煤岩体的密度，kg/m3；g 为重力加速度，m/s2。

对于具有多孔介质特性的煤岩，当不考虑煤岩骨架形变时，钻井液滤失控制方程[16]为：

式中：ρl为钻井液密度，kg/m3；μ 为钻井液黏度，Pa·s；κ 为煤岩渗透率，m2；t 为时间，s；Qm为源汇项，此处为0，kg/（m3·s）；S 为煤岩储水系数，Pa-1。

S 可以表示为：

式中：φ 为煤岩孔隙度；Ks为煤岩骨架体积模量，Pa；Kl为钻井液体积模量，Pa。

实际上，煤岩骨架的形变，将改变孔隙压力，根据有效应力原理，煤岩挤压变形时，孔隙压力将增大，煤岩体积扩大时，孔隙压力将减小，若以体积应变表征煤岩形变，则式（4）可以修正为：

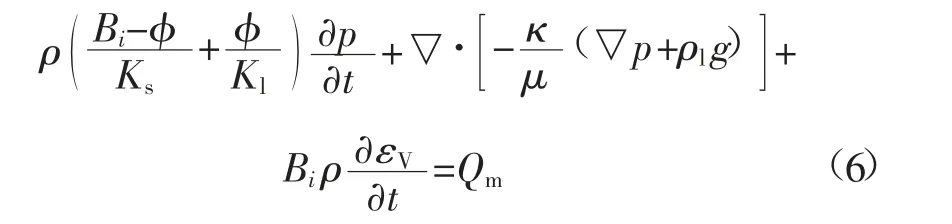
式中：εV为体积应变，无量纲。

根据岩石力学理论[17]，应变和位移关系满足：

式中：εij为应变分量，无量纲；μi，j、μj，i为位移偏导数，无量纲；i、j 为坐标轴分量。

体积应变εV可以表示为：

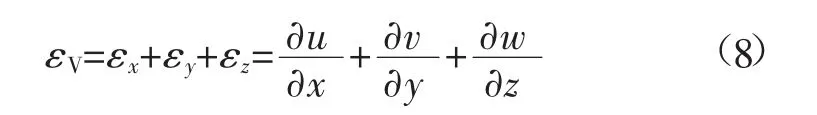
式中：εx、εy、εz分别为x、y、z 轴方向的应变分量，无量纲；u、v、w 分别为x、y、z 轴方向的位移分量，m。

煤岩体积改变，不仅会导致孔隙压力变化，还将影响煤岩渗透率[18]，C Louis 通过大量实验确定了渗透率与有效应力间的经验关系[19]：

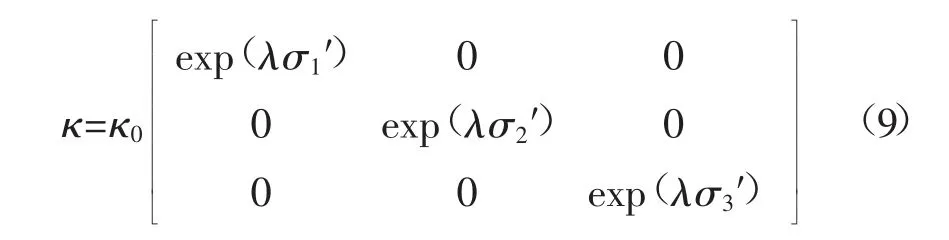
式中：κ0为煤岩初始渗透率，m2；σ1′、σ2′、σ3′为煤岩有效应力分量，Pa；λ 为渗透率各向异性系数，一般通过实验确定，取λ=0.35 MPa-1。

由式（6）、式（8）、式（9）可得，考虑煤岩变形对孔隙压力和渗透率影响的钻井液滤失控制方程为：

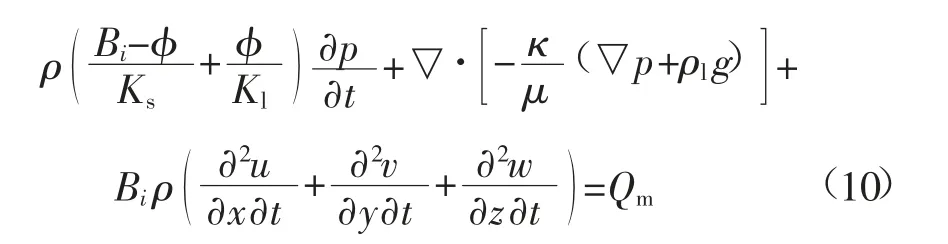
联立式（3）和式（10），即为考虑钻井液滤失和煤岩骨架相互作用的煤岩流固耦合模型，根据煤岩钻进时的原始地应力、井眼轨迹、钻井液等工况条件，即可确定钻井液滤失对煤岩应力场和渗流场的影响[20]，再结合岩石破坏准则，即可对煤岩井壁的稳定性进行评价。

2 煤岩井壁稳定性评价模型的建立

2.1 定向井井壁应力模型

为了提高井壁稳定评价模型的通用性，建模时考虑井斜角、方位角等井眼轨迹参数的变化[21]。若煤岩上覆岩层压力为σV、最大水平地应力为σH、最小水平地应力为σh，根据σV、σH、σh的关系，可以建立大地坐标系（1，2，3）。为求解方便，建立井眼坐标系（x，y，z），其中，oz 轴与井眼轴线重合，ox 轴和oy 轴所在平面垂直于井眼轴线，且ox 轴沿着σH的方位。模型坐标系如图2。

图2 中，σx、σy、σz分别为井眼坐标系中x，y，z方向的应力，Pa；τxy、τyz、τxz为井眼坐标系中的切应力，Pa；σV为上覆岩层压力，Pa；σH为最大水平地应力，Pa；σh为最小水平地应力，Pa；α 为井斜角，（°）；β为井斜方位与σH方位间的夹角，（°）。

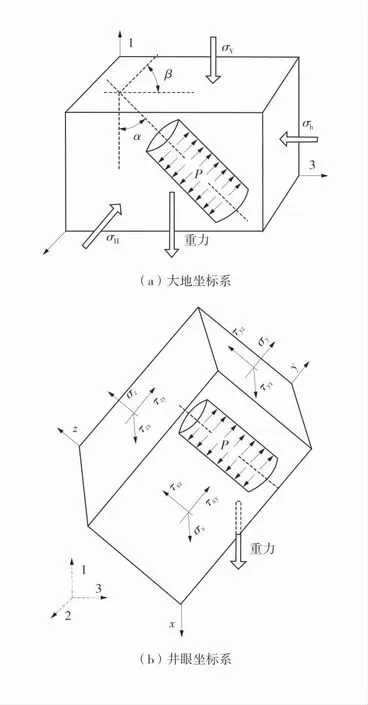
图2 模型坐标系Fig.2 Coordinate systems of model

根据井眼坐标与大地坐标间的对应关系，可以确定井眼坐标系下井壁煤岩有效应力张量为σ′：

其中，各应力分量分别为[22]：

式中：σx、σy、σz分别为井眼坐标系中x、y、z 方向的应力，Pa；τxy、τyz、τxz为井眼坐标系中的切应力，Pa；σV为上覆岩层压力，Pa；σH为最大水平地应力，Pa；σh为最小水平地应力，Pa；为井斜角，（°）；β 为井斜方位与σH方位间的夹角，（°）。

2.2 煤岩破坏准则及定解条件

由于煤岩存在割理缺陷，当割理面上的剪应力超过煤岩本身抗剪强度和作用于该面上由法向应力引起的摩擦力之和时，煤岩将发生破坏，因此采用Mohr-Coulomb 塑性模型判断井壁煤岩破坏[23]：

式中：φ 为煤岩内摩擦角，（°）；C 为煤岩黏聚力，MPa；σ1′为最大主应力；σ3′为最小主应力。

若已知初始地应力、地层初始孔隙压力、井筒液柱压力等流固耦合模型定解条件，流固耦合模型的定解条件见表1，便可通过流固耦合模型确定井壁煤岩应力场和渗流场，当煤岩有效应力达到Mohr-Coulomb 破坏准则时，井壁煤岩将发生破坏。

表1 流固耦合模型的定解条件Table 1 The solution conditions of fluid-solid coupling model

3 煤岩井壁稳定性数值模拟

为了分析钻井液滤失对煤岩应力场和渗流场的影响，选取新疆乌鲁木齐市乌东矿区X 井进行实例分析，该井钻至900 m 时的钻井液密度虽然接近1.2 g/cm3，但仍然发生了遇阻情况，后期井径测井表明，该处发生井壁失稳。为了揭示该现象的原因，建立模型并进行了分析。

考虑到井眼轴向与径向之比较大，为了降低计算量，将三维井壁煤岩物理模型简化为二维，建立的二维平面应变模型如图3；为了提高计算精度，采用结构化映射方法对模型进行网格划分，为了提高模拟精度，对近井壁区域进行局部网格细化，模型参数见表2。

根据钻井液与煤岩相互作用的流固耦合数学模型和二维井壁稳定性评价模型，通过数值方法对模型进行了计算，获得了相应的应力场和渗流场。钻井液滤失对煤岩应力场、渗流场的影响如图4～图7。

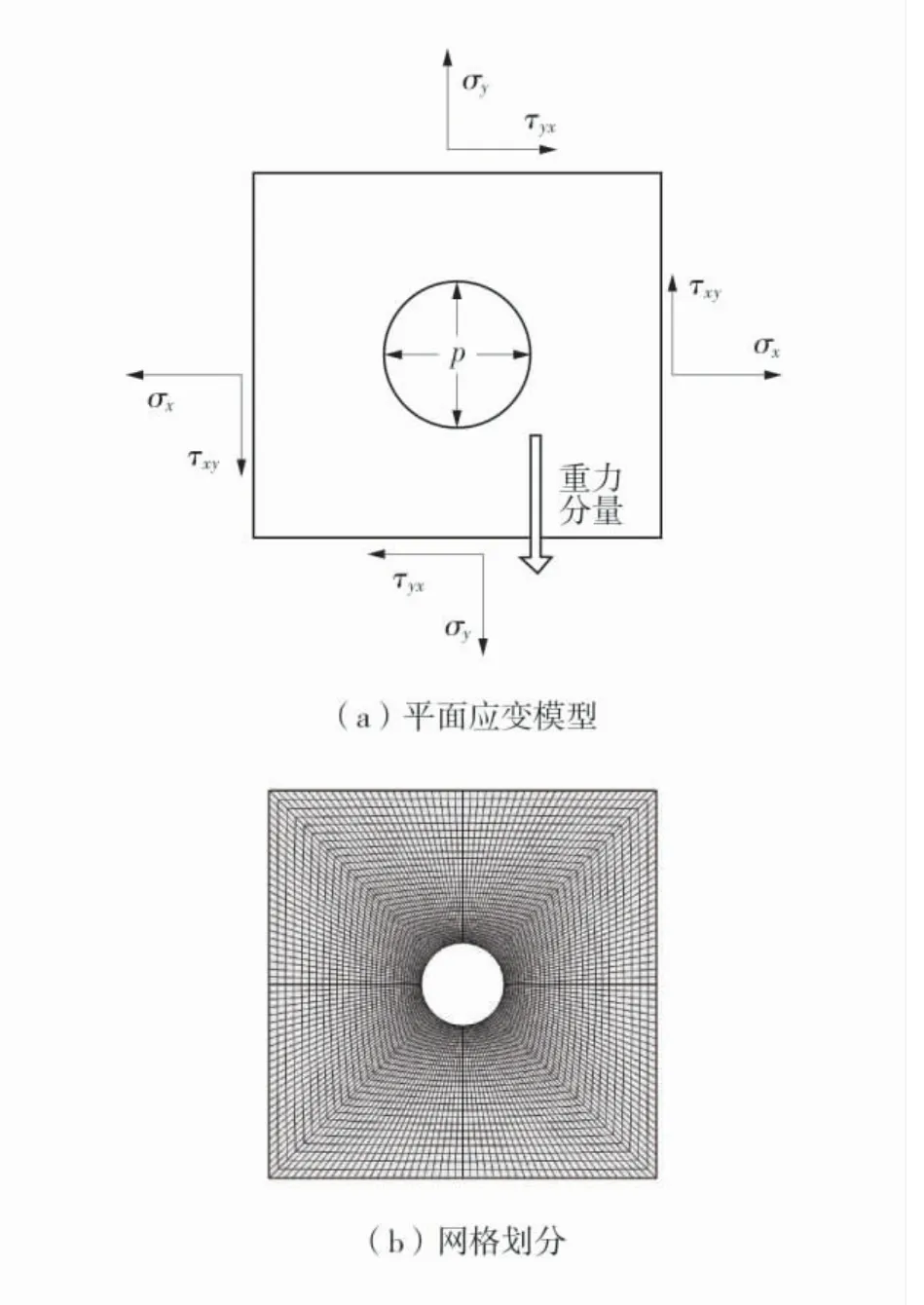
图3 二维井壁煤岩数值模型Fig.3 2D numerical model of coal wellbore

表2 主要模型参数Table 2 Main parameters of model

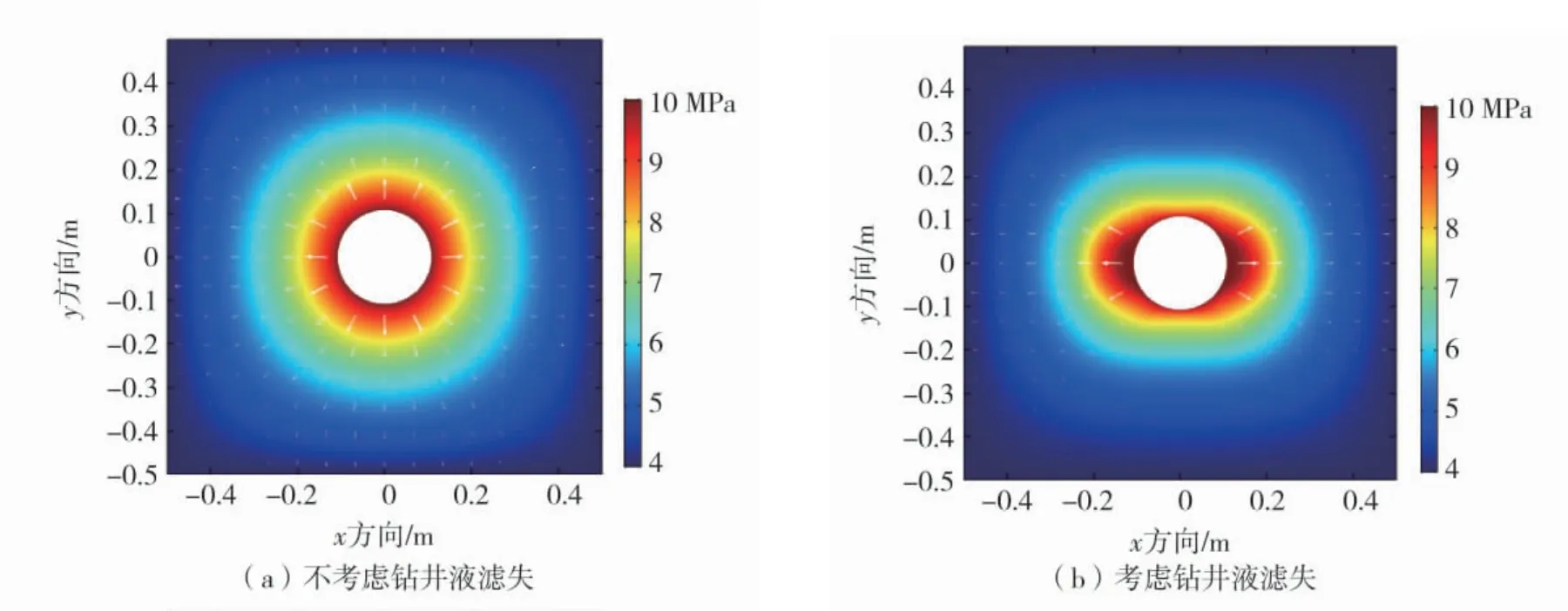
图4 钻井液滤失对孔隙压力的影响Fig.4 Effect of drilling fluid loss on pore pressure

图5 煤岩变形对渗流场的影响Fig.5 Effect of coal rock deformation on seepage field

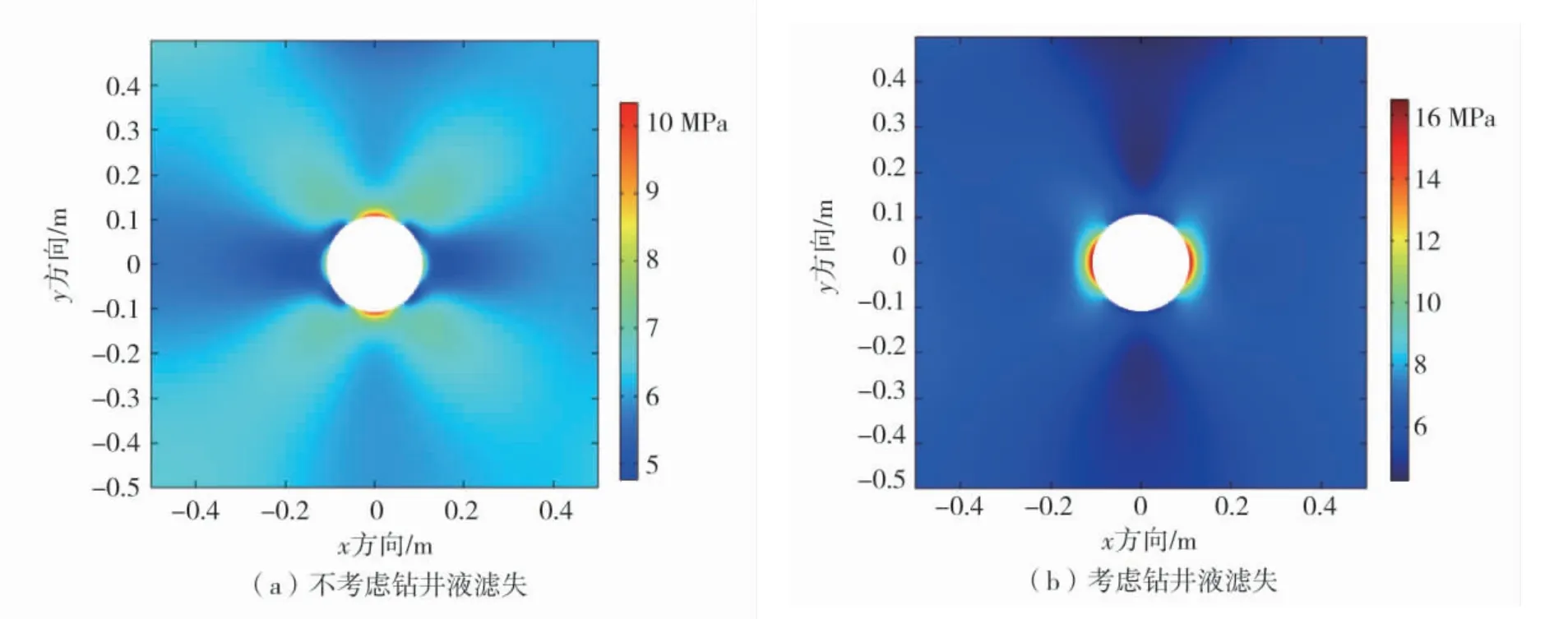
图6 钻井液滤失对煤岩应力场的影响Fig.6 Effect of drilling fluid loss on stress field of coal and rock

对比分析图4～图6 可以看出，钻井液滤失对应力场、渗流场影响较大，不均匀地应力的挤压作用使钻井液容易沿着最大水平地应力方向滤失；而钻井液滤失会导致孔隙压力增大，继而使井壁煤岩的应力发生改变，应力场最大值由最大水平地应力方向转移到了最小水平地应力方向，且应力极值由15 MPa 增至17 MPa。因此，钻井液滤失对井壁煤岩的稳定性影响较大。

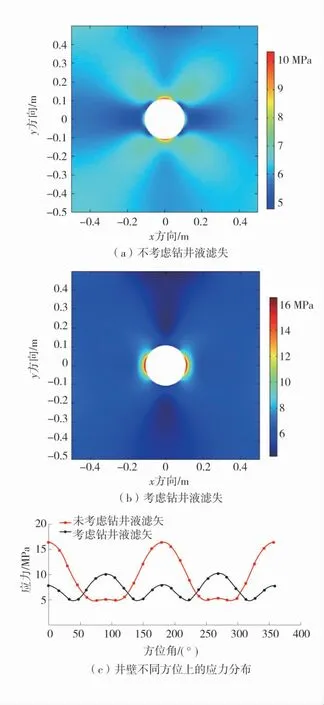
图7 钻井液滤失对井壁不同方位处应力的影响Fig.7 Influence of drilling fluid loss on borehole stress in different azimuth

通常认为，提高钻井液密度能够起到支撑井壁的作用，对于X 井来说，钻井液密度已达1.2 g/cm3，若不考虑钻井液对煤岩的化学作用，按常规认识不应发生井壁失稳现象。为此，对钻井液密度对煤岩井壁应力的影响进行了分析，钻井液密度对井壁不同方位处应力的影响如图8，可以看出，在一定范围内提高钻井液密度时，煤岩井壁上应力反而增大，这是由于密度增大会使钻进液向煤岩滤失，从而引起孔隙压力增大，最终导致煤岩应力增大，这是不利于井壁稳定的。

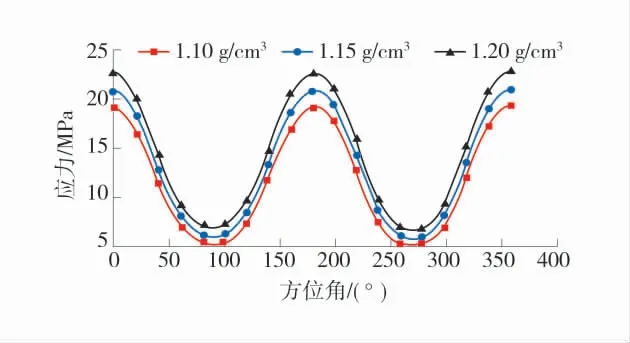
图8 钻井液密度对井壁不同方位处应力的影响Fig.8 Influence of drilling fluid density on borehole stress in different azimuth

4 结 论

1）考虑钻井液滤失对煤岩应力场、渗流场的影响，建立了评价煤岩井壁稳定性评价的流固耦合模型，并通过数值方法对模型进行了求解，为煤岩井壁稳定性评价提供了理论指导。

2）钻井液滤失对煤岩应力场、渗流场影响较大，不均匀地应力的挤压作用，使钻井液容易沿着最大水平地应力方向滤失；在一定范围内提高钻井液密度，钻井液容易侵入煤岩孔隙，导致孔隙压力增大，使煤岩应力极值增大，不利于井壁稳定。

3）钻井液滤失引起的流固耦合属于物理作用，对于具有水化分散特性的煤岩，还需考虑钻井液与煤岩矿物间的化学反应，进一步完善煤岩井壁失稳理论。