基于质量竞争的安全生鲜农产品供应链网络设计*

周二鹏

(安徽电子信息职业技术学院 经济管理系，安徽 蚌埠 233030)

0 引 言

生鲜农产品对人类健康至关重要，农产品的质量关系到食品的安全。全球供应链都在不断发展以满足消费者对新鲜农产品的需求，随着新鲜农产品的生产商和消费者均遍及全球，农产品供应链对确保产品质量至关重要。本研究考虑具有竞争性的生鲜农产品供应链，以最大化农产品公司利润为目标，设计合适的供应链网络。

1 质量衰减函数

首先介绍质量衰减函数的相关内容，然后推导出带有质量衰减的供应链路径模型。新鲜食品容易变质，随着时间的流逝其质量会下降[1]。食品质量恶化的速度是一个关于微环境、气体成分、相对湿度和温度的函数。随着时间t的变化，食物的质量Q通过如下的微分方程来表示：

(1)

其中，k是反应速率，由Arrhenius公式定义，即k=Ae(-E/RT)。A是指数常数，T是温度，E是活化能，R是通用气体常数[2]。参数n是反应阶数。如果反应阶数为零，即∂Q/∂t=-k。初始质量用Q0表示，剩余质量Qt可以表示为：

Qt=Q0-kt

(2)

另一方面，如果反应阶数为1(称为一阶反应)，则质量衰减函数由以下表达式给出：

Qt=Q0e-kt

(3)

服从质量衰减的生鲜农产品有桃子、苹果、豌豆、豆类、胡萝卜等等[3-4]。

图1 供应链网络拓扑

将路径p定义为有向链接的序列，这些有向链接将公司节点i(源节点)与零售店节点k(目的地节点)相连接。令βb表示对于链路b的质量衰减，βb取决于链接b上的反应阶数n、反应速率kb和时间tb，即

(4)

kb是与链路b关联的反应常数。假设在生产和收割环节没有质量衰减。由于路径上的每个链路可能具有不同的温度条件，因此必须区分链路温度。通过Arrhenius公式重新描述每个链路的反应速率，如下所示：

kb=Ae(-E/RTb)

(5)

(6)

2 供应链的竞争博弈模型

xp≥0

(7)

(8)

与每个食品公司i在每个链路上的流必须遵循流守恒原则，即

(9)

其中，fl表示链路l上的流。δlp=1说明链路l包含在路径p中。另外，链路上的流不能超过链路的容量ul，即

fl≤ul

(10)

结合约束条件(9)和(10)，有

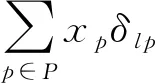
(11)

(12)

食品公司i在零售商店k上的新鲜食品的需求用dik表示，有

∑xp=dik

(13)

食品公司i在特定零售商店的产品价格不仅取决于其产品的需求和平均质量，还取决于所有零售中其他可替代食品的需求和平均质量。假定这些需求价格函数是连续的、可微的和单调递减的。用ρik表示食品公司i在零售商店k产品的需求价格，并假设有

(14)

(15)

此外，将与供应链网络中其余链路的运营成本函数定义为

(16)

食品公司i的效用是其利润，定义为收入与总成本之差。其中总成本由生产和收割环节的总成本和供应后收割环节的总运营成本组成。公司i的效用Ui可以表示为

(17)

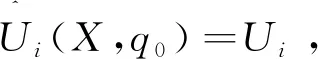
(18)

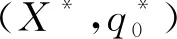
(22)

3 算法设计

设计了一个计算变分不等式的算法以得到上述竞争博弈模型的解。用于计算变分不等等式(22)的解的算法为：确定Y*∈K，Y是RN中的一个向量，F(Y)是一个连续的函数，使得F(Y):XK⊂RN以及

≥0

(23)

其中，<·,·>表示N维欧几里得空间的内积。在第τ+1次迭代中，有

Yτ+1=PK(Yτ-ατF(Yτ))

(24)

其中，PK是可行集合K的投影。

在第τ+1次迭代中，新鲜产品路径流的解析式如下所示：

(25)

采用梯度下降算法(如算法1所示)，以迭代的方式求得xp的值。同理，下面的q0a、λa和γa均可以使用算法1进行求解。

算法1 梯度下降算法输入:误差阈值ε、下降步长ατ、最大迭代次数τMAX输出:xp//初始化x0p←0;τ←0;Ω←ρ^ik(x0p,qτ0)+∑∂ρ^ij(x0p,qτ0)∂x0p×∑xτr-∂Z^i(x0p,qiτ0)∂x0p-∂C^i(x0p)∂x0p-∑γτlδlp;while τ<τMAX or ατ×Ω>ε doτ←τ + 1; 使用式(25)更新xτp的值;end whilexp←xτpreturn xp;

(26)

与每一条链路a初始质量相关联的拉格朗日乘子λ的计算方式如下所示：

(27)

与每一条链路l链路容量相关联的拉格朗日乘子γ的计算方式如下所示：

(28)

4 案例分析

(1)案例一

在案例一中，假设零售商的消费者会辨别来自不同公司的桃子质量。零售商R1对公司1和公司2的相应需求价格函数如下：

零售商R2对公司1和公司2的相应需求价格函数如下：

在表1和2中，展示了由本模型求解得到的纳什均衡解。

表1 纳什均衡解(链路流、初始质量以及拉格朗日乘子)

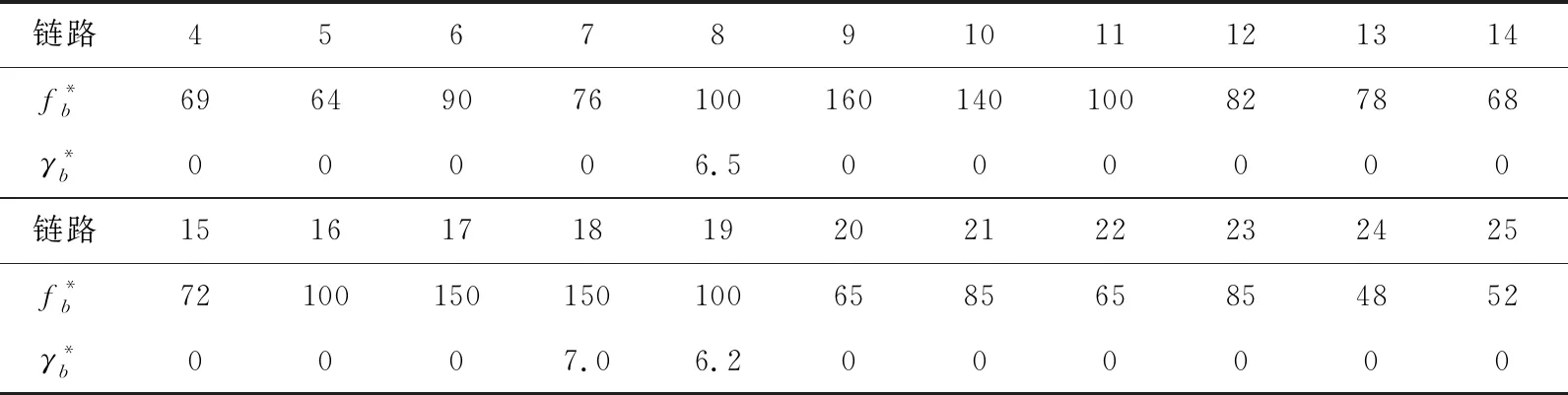
表2 纳什均衡解(链路流以及拉格朗日乘子)

公司1和公司2的利润分别为：

U1=3302,U2=788

(2)案例二

在案例二中，考虑了自然灾害对供应链的影响。自然灾害会影响两个公司的生产能力，极端的寒冷天气会使桃子作物减产。在表3和表4展示了案例二的纳什均衡解。

表3 纳什均衡解(链路流、初始质量以及拉格朗日乘子)

表4 纳什均衡解(链路流以及拉格朗日乘子)

在案例二中公司1和公司2的利润分别为：

U1=2984.1,U2=675.7

5 结 论

本研究建立了竞争性新鲜农产品供应链网络解决方案的模型和通用框架。在该框架中，食品公司会最大程度地提高自身利润，同时确定新鲜农产品的初始质量和相关成本。然后，展示了纳什均衡存在的条件，并设计了相应的算法。最后，将本框架应用于案例分析研究。未来的研究工作在于将本框架应用于真实的供应链设计，并与其他框架进行对比，以进一步调整和优化本框架。