聚芳砜酰胺溶液干喷湿纺的动力学模拟计算

王建宁， 张玉梅，王华平

(东华大学 a.材料科学与工程学院；b.纤维材料改性国家重点实验室，上海 201620)

湿法纺丝获得的聚芳砜酰胺(PSA)纤维虽然具有耐高温、阻燃(极限氧指数>33% )、高温尺寸稳定性等特性[1-4]，但力学性能的不足限制了该纤维的发展。文献[5-7]研究表明：PSA分子结构中砜基的非平面结构和空间位阻效应，致使其无论是在溶液中还是在固态下都无法呈现刚直的“直线”结构，且结晶温度高、结晶速度低；PSA分子结构中酰胺键的存在增加了分子间的氢键作用，使得PSA一旦固化就很难通过拉伸获得较高的取向和结晶结构。湿法纺丝在凝固浴中的喷头拉伸为“负拉伸”或“零拉伸”，使得PSA溶液在喷丝微孔中因剪切产生的取向在挤出胀大过程中又发生解取向。凝固产生的凝胶网络基本呈无规则状态，而依靠后续拉伸来提高PSA纤维分子链段有序排列的效果是有限的[8-10]。笔者等[11]探索了利用干喷湿纺的方法提高PSA纤维力学性能的可行性，研究发现，凝固丝条的取向程度相比湿法纺丝有较大提高，且强度也有所增大，但该工作目前仅限于实验室阶段。PSA溶液是否具有干喷湿纺规模放大的工程可行性尚需探讨。

文献[12-14]研究表明，聚合物溶液干喷湿纺的关键在于喷丝孔的挤出情况，影响因素包括溶液的流变特性、纺丝温度、泵供量(挤出速度)、空气段条件、喷头拉伸比及喷丝孔结构等。贺福[14]研究发现，在干喷湿纺过程中，漫流是影响连续生产的一大技术难题。喷丝板的表面张力大于细流的表面张力、喷丝孔的长径比与拉伸速度较小以及断丝等都会导致漫流的形成。曾小梅等[15]研究发现：喷丝孔较小、喷丝孔中溶液剪切速度较大导致溶液的弹性形变较大以及出口胀大比增大；此外，较大的溶液黏度、较低的纺丝温度及较少的滤布层数都会导致较大的出口胀大比。综上所述，各因素交错影响纺丝过程，单纯的试验方法难以全面认识非平衡态过程的复杂变化，而模拟计算可提供纤维所有参数的变化路径，对理解和预测纺丝过程中纤维非平衡态结构的形成是至关重要的。笔者等[16]结合纺丝试验与动力学模拟法研究了聚丙烯腈(PAN)溶液干喷湿纺的可纺性，模拟计算发现，可以将喷丝板前压力作为可纺性的判据，无论改变喷丝孔直径和长度等结构参数，还是改变纺丝温度和泵供量等纺丝条件，都会导致漫流现象。类比可知，PSA和PAN所用溶剂相近，因而溶液与喷丝板的表面张力相近，初步判断此模拟计算方法可以用于PSA溶液干喷湿纺的挤出拉伸研究。文献[17]研究发现，用于PAN干喷湿纺的溶液，可以在较宽的范围内通过改变PAN相对分子质量及其质量分数来调整溶液的黏弹性，且PAN凝固成形后的纤维具有较高的后拉伸形变能力，因而可以在较大范围内调控喷丝板结构参数、挤出速度、喷头拉伸比，从而达到提高纤维可纺性的目的[18-19]。然而，PSA溶液流变特性、分子间作用力及形变能力与PAN存在较大差异[9, 20]，由此可见，满足PSA溶液干喷湿纺可纺性的临界条件尚不能简单推测。

本文通过挤出拉伸动力学模拟计算来获取满足PSA溶液干喷湿纺的工程条件和工艺条件，主要模拟计算不同纺丝参数(喷丝板孔径和孔长、纺丝温度、挤出速度、喷头拉伸比和空气段长度等)下的板前压力，以及空气段丝条直径、胀大比、温度、速度和应力，求取喷丝板结构参数、挤出速度、空气段长度、喷头拉伸比等达到顺利干喷湿纺的临界条件，为PSA溶液干喷湿纺的喷丝板设计和挤出拉伸条件优化提供参考依据。

1 试 验

1.1 原料和方法

PSA纺丝溶液(上海特安纶纤维有限公司提供)，以4，4′- 二氨基二苯基砜(4,4′-DDS)、3，3′- 二氨基二苯基砜(3,3′-DDS)及对苯二甲酰氯(terephthaloyl chloride，TPC)为单体，摩尔比为3∶1∶4，在溶剂N,N′ - 二甲基乙酰胺(DMAc)中低温(5 ℃)缩聚合成，反应过程中加入Ca(OH)2中和反应的副产物氯化氢。溶液中PSA的质量分数为23%，在25 ℃时用乌氏黏度计在DMSO中测得PSA溶液的特性黏度为1.80 dL/g。

1.2 流变测试

利用MCR301型高级旋转流变仪(奥地利安东帕公司)进行稳态扫描。试验时选用直径为25 mm的平行板转子，间距设为1 mm。为防止试验中因样品吸水及溶剂挥发而影响试验结果的准确性，需在样品接触空气的自由表面均匀涂抹一层硅油。稳态扫描剪切速度范围为0.1～100.0 s-1，测试温度为30～60 ℃。

1.3 纺丝试验

采用实验室干喷湿纺试验线进行纺丝，喷丝板规格为40孔，喷丝孔直径为0.15 mm，长径比为3∶1，凝固浴为DMAc水溶液。纺丝条件为空气段长度30.00 mm、凝固浴体积分数40%、温度40 ℃。保持纺丝条件不变，改变纺丝溶液的温度，并调节计量泵泵供量和第一辊拉伸速度(保持喷头拉伸比不变)，观察溶液的挤出情况。

2 干喷湿纺动力学模型描述

2.1 几何模型与网格划分

干喷湿纺成形过程包括纺丝溶液输送、喷丝孔入口收缩流动、喷丝孔内挤出流动、喷丝孔出口胀大、空气段拉伸、凝固成形和拉伸阶段[21]，研究溶液的可纺性，主要涉及纺丝溶液在喷丝孔内的收缩流动和挤出胀大以及干喷段的拉伸流动，此过程的二维几何模型示意图如图1所示。

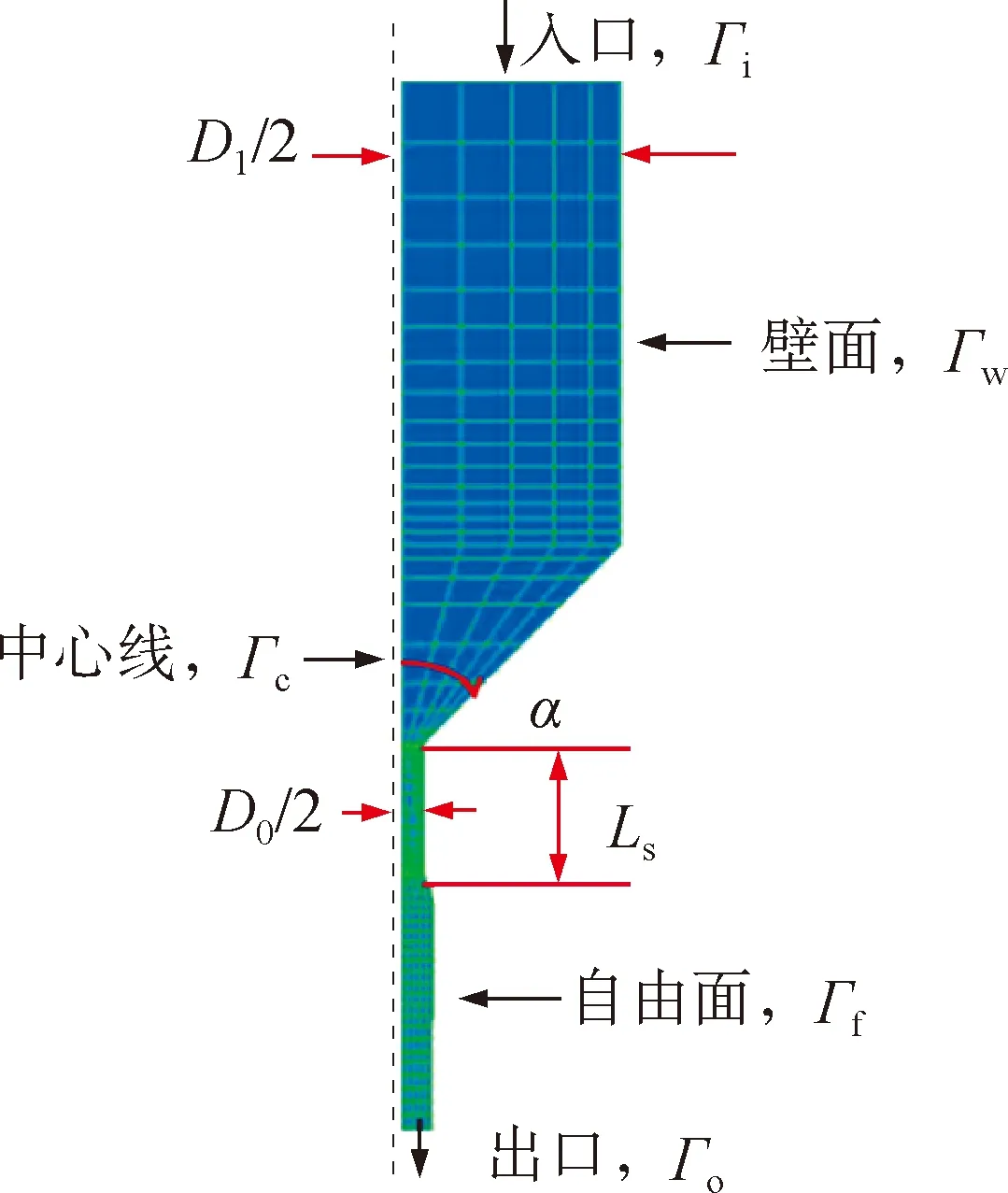
图1 Polyflow模拟计算的二维模型与网格划分Fig.1 2D spinning model and finite-element mesh of simulation by Polyflow

2.2 动力学模型方程描述

文献[16, 21]所描述的溶液干喷湿纺动力学模型如下所述：

(1) 连续性方程。PSA/DMAc浓溶液在整个干喷湿纺纺丝过程中，由于空气段距离较短(30 mm)且温度较低，忽略丝条与冷却介质之间的传质，挤出拉伸流动过程中的二维稳态连续性方程如式(1)所示。

∇·v=0

(1)

式中：v为丝条的速度。

(2) 动量方程。由于PSA/DMAc溶液的黏度较大，在挤出喷丝孔后的拉丝过程中，空气摩擦力和表面张力数值比重力和惯性力小几个数量级，在计算过程中可忽略这两个力。因此，黏弹性流体在流动过程中动量的变化主要由重力、静态液压力和黏弹力等3种外力贡献。动量方程如式(2)所示。

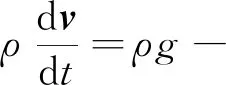
(2)

式中：ρ为溶液密度(对于溶剂和聚合物体系，密度是质量分数和温度的函数)；g为重力加速度(取9.8 m/s2)；p为静态液压力(液体处于静止或者相对静止时，液体单位面积上所受的法向作用压力)；τ为应力张量。

(3) 能量方程。在PSA/DMAc溶液干喷湿纺纺丝过程中，未发生相转变，忽略丝条的轴向传热，只考虑丝条与冷却介质的热传递过程和黏弹性流体流动中的功交换过程。能量方程如式(3)所示。

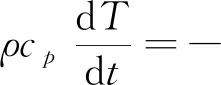
(3)

式中：cp为溶液的比定压热容；q为热通量。

(4) 本构方程。以40 ℃时的流变数据为例，剪切黏度(η)与第一法向应力差(N1)符合PTT(Phan-Thien-Tanner)模型(见式(4))，得到的主曲线如图2所示。

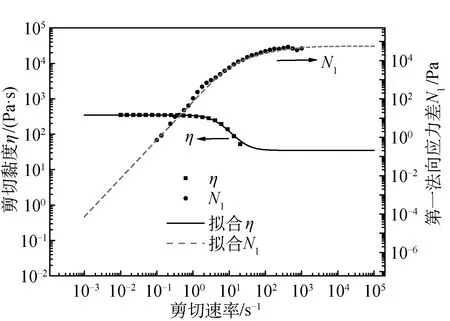
图2 40 ℃下PSA/DMAc溶液的剪切黏度和第一法向应力差以及PTT模型拟合的曲线Fig.2 Measured shear viscosity and first normal stress difference of PSA/DMAc solution at 40 ℃ and fit with the PTT model

(4)

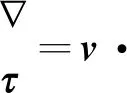
(5)

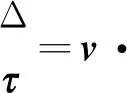
(6)

(7)

假设溶液的黏弹性对温度的依赖关系满足时温等效原理，则松弛时间λ、聚合物黏度η与温度T的关系[21]可表示为

λ(T)=αTλ(T0)

(8)

η(T)=αTη(T0)

(9)

式中：T和T0分别为聚合物溶液的绝对温度和参考绝对温度；αT为转换因子，可通过式(10)求得。

(10)

式中：ΔH为黏流活化能；R为气体常数，R=8.314 J/(K·mol)。

PTT模型中的参数可由图2所示拟合曲线得到，不同温度下PSA/DMAc溶液的PTT模型参数如表1所示。

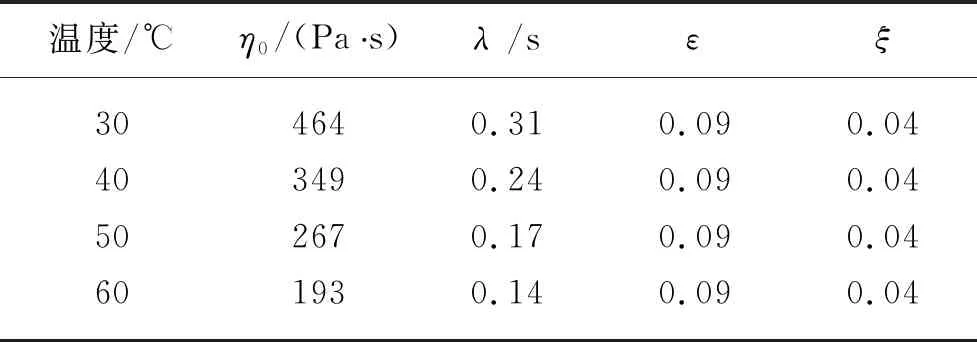
表1 PSA/DMAc溶液不同温度下PTT模型的溶液参数Table 1 Parameters of PTT model for PSA/DMAc solution at various temperature

动力学方程中所涉及的其他材料参数如表2所示。

表2 动力学模拟方程所用的PSA/DMAc溶液材料参数Table 2 Parameters of PSA/DMAc solution for dynamic simulation equations

2.3 边界条件

Polyflow模拟计算需要规定流体沿计算区域流动的边界条件，如图1所示，其中Γi、Γw、Γf、Γc、Γo分别为入口、壁面、自由面、中心线和出口的边界。边界条件又分为流动边界条件和热量边界条件。根据干喷湿纺模拟计算的要求，分别设置边界条件如下：

(1) 入口边界。喷丝孔入口处的边界，根据计量泵挤出速度得到入口速度，根据纺丝温度得到入口温度。Γi：v=v(r)，τP=τP(r)，T=Ti。

(2) 喷丝孔壁面。壁面无滑移，滑移速度为零。纺丝溶液釜的水浴温度与溶液温度相同，不存在热传导，故设温度绝缘。Γw：v= 0，T=Tw。

(3) 对称中心轴。Γc：vr= 0，τ·nt= 0，q·n= 0。

(4) 自由表面。自由面上法向速度为零，由于对流传热的存在，要设置热通量。Γf：τ·n= 0，v·n= 0，q·n=h(T-Tamb)

(5) 流动出口。在此界面施加凝固浴拉伸速度，温度设为边界绝缘。Γo：vz=vi，Fr= 0，q·n= 0。

其中：Ti为进口温度；Tw为壁面温度；Tamb为环境温度；n和t为法向和切向的单位矢量；q为热通量；vi为丝条进入凝固浴时的拉伸速度；Fr为径向的拉伸力；h为对流传热系数。

3 结果与讨论

3.1 PSA溶液的干喷湿纺可纺性试验

根据聚合物溶液挤出成形的影响因素[14-16]，在溶液表面张力基本不变的情况下，增大溶液黏度η、喷丝孔半径R0、挤出速度v0，挤出细流由液滴型转变为漫流型，直到挤出正常的胀大型，对于特定的溶液，是否能够正常挤出，总是存在临界喷丝孔径RC和临界挤出速度vC。为试验PSA/DMAc溶液干喷湿纺的临界挤出条件，分别改变纺丝温度、喷丝孔径(Ls∶D0=3∶1)和挤出速度(泵供量)，初步确定满足PSA/DMAc溶液干喷湿纺的临界喷丝孔径RC和临界挤出速度vC。不同温度下PSA溶液黏度与剪切速率的关系如图3所示，其中，PSA质量分数为23%，特性黏度为1.8 dL/g。

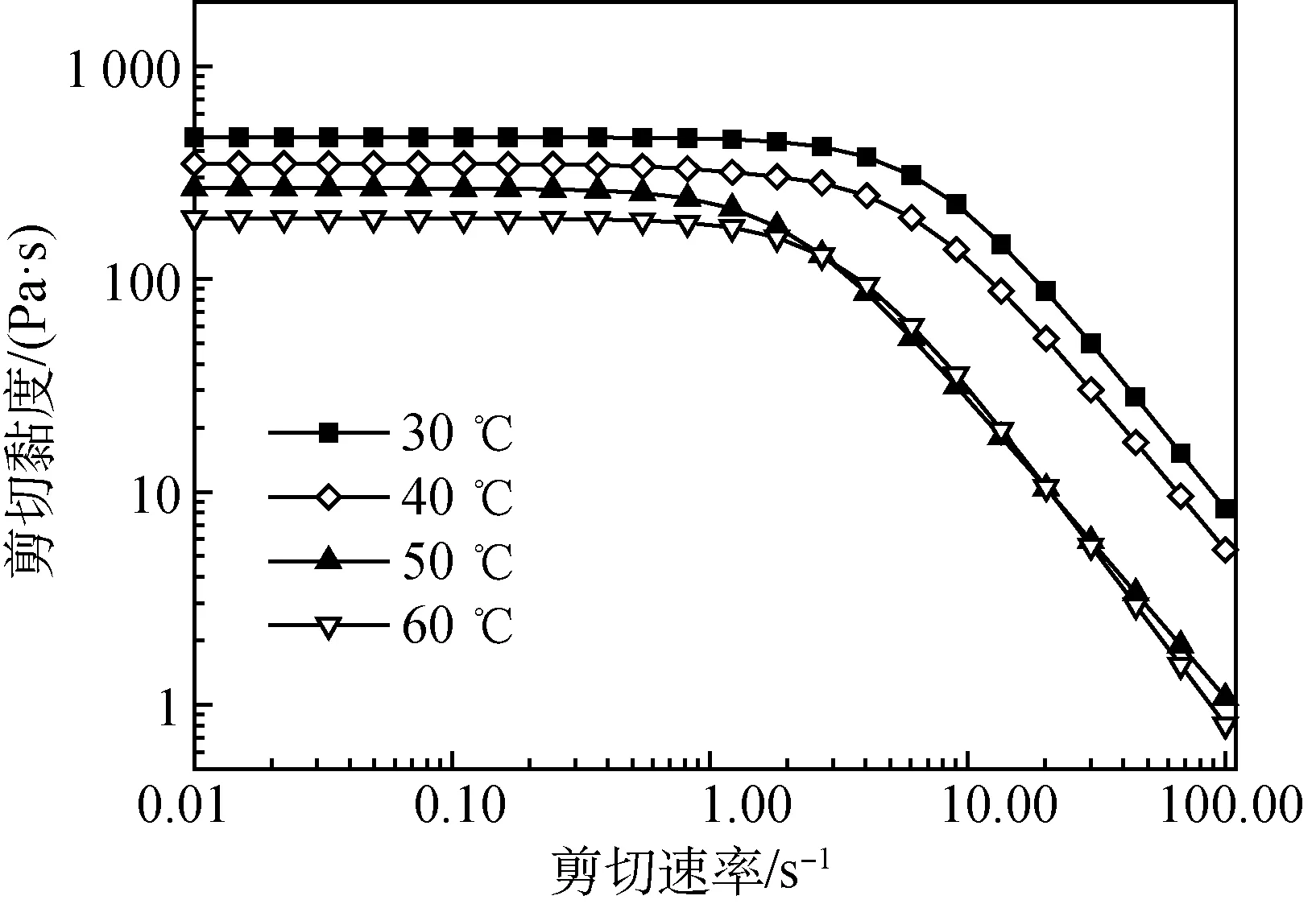
图3 不同温度下PSA溶液黏度与剪切速率的关系Fig.3 The relationship between viscosity and shear rate of PSA solution at different temperatures

需要说明的是，采用直接聚合法制备的PSA/DMAc溶液，受PSA相对分子质量和溶解度的限制，温度降到室温附近(如30 ℃)，所获得溶液零剪切黏度最高只能达到464 Pa⋅s(见图3)，以此溶液进行干喷湿纺挤出试验。当喷丝孔直径为0.10 mm、挤出速度增大到6.9 m/min时，直到出现纺丝组件漏料现象，也未实现正常挤出；当喷丝孔直径为0.12 mm、挤出速度增大到4.8 m/min时，溶液才能够正常挤出。初步判断用于此溶液的临界喷丝孔径RC约为0.06 mm。根据该挤出条件推算后续的拉伸倍率和速度，按0.12 mm丝条直径来推算，若要制备直径约为20 μm的PSA纤维，那么总拉伸倍数高达36倍，而PSA成形后的拉伸倍数一般不超过4倍，这意味着需要高达9倍的喷头拉伸比以及高达40 m/min的一辊速度，这对于PSA溶液显然是不可行的。因此，若要实现PSA/DMAc溶液干喷湿纺的正常挤出，只有选用更大的喷丝孔径。当喷丝孔径为0.15 mm时，溶液可以在较宽的纺丝温度和挤出速度范围内实现干喷湿纺的正常挤出。采用0.15 mm(Ls∶D0=3∶1)的喷丝孔径，在不同的纺丝条件下，PSA/DMAc溶液的干喷湿纺临界可纺条件，即正常挤出成形的临界条件，包括纺丝温度、溶液黏度和泵供量(挤出速度)，列于表3。

表3 满足PSA/DMAc溶液正常挤出成形的临界纺丝条件Table 3 The critical spinning conditions for normal extrusion of PSA/DMAc solution

3.2 满足PSA/DMAc溶液干喷湿纺可纺性的临界板前压力

文献[16]通过溶液挤出模拟计算法，获得满足PSA/DMAc溶液干喷湿纺的板前压力，作为预测其可纺性的依据。设定以下纺丝参数不变：喷丝板入口直径D1=1 mm，出口直径D0=0.15 mm，喷丝孔长径比Ls∶D0=3∶1，入口角α=45°，喷丝头拉伸比λ=1.5，空气段长度L=30 mm，空气段环境温度Tamb=20 ℃。改变纺丝温度T0和泵供量W进行模拟计算，探究PSA/DMAc溶液干喷湿纺过程中的喷丝孔压力降和挤出胀大情况，判断其满足正常挤出的临界条件。可纺条件下沿纺程丝条物性参数的分布如图4所示。

从图4(a)可以看出，丝条沿纺程速度梯度的变化主要集中在喷丝孔内流动和出口胀大处。PSA/DMAc溶液在顺利挤出可纺的条件下，喷丝孔内压力分布接近，入口压力约为6.0 MPa，如图4(b)所示，类似于PAN溶液干喷湿纺的可纺性模拟，满足可纺性的共同特点是喷丝孔内压力分布接近，仍然可以将板前压力作为干喷湿纺挤出可纺性的判据。但相比PAN溶液[16]，PSA溶液需要达到更高的零剪切黏度值，才能保证在同样的喷丝孔参数和挤出条件下顺利挤出。这是由于PSA的分子结构不同于PAN，前者溶液更容易剪切变稀，在同样剪切速度下表面黏度值更小，能够更好地提供模拟试验条件下的动态数据。

因喷丝孔结构参数和喷头拉伸比相同，沿纺程的丝条直径变化相近，升高温度，出口胀大比只是略微下降，但变化不大，如图4(c)所示。因此，出口胀大比可以作为挤出可纺性的参考指标，PSA溶液在出口胀大比<1.5时可纺性较好，其胀大比的值比PAN模拟的结果略大，这说明PSA溶液切力变稀更加明显，更易发生出口胀大，喷丝孔中取向的分子链解取向程度更高，经后续拉伸后更难得到取向较高的丝条。

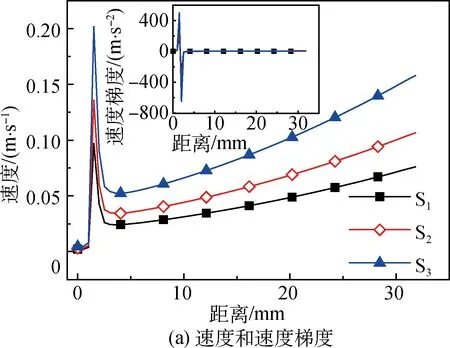
图4 可纺条件下沿纺程丝条物性参数的分布Fig.4 Physical parameters distribution along spinning-line critical extrusion spinnable conditions

3.3 喷丝孔参数变化对PSA/DMAc溶液干喷湿纺动力学的影响

上述试验和模拟结果提供了可纺性的判据，根据该判据可进一步进行喷丝板结构参数的模拟计算，研究喷丝孔直径和长度对PSA/DMAc溶液干喷湿纺挤出可纺性的影响。

3.3.1 喷丝孔直径(长径比)对溶液挤出的影响

设定PSA/DMAc溶液的参数：溶液温度T0=40 ℃，喷丝板入口直径D1=1 mm，入口角α=45°，喷丝孔长度Ls=0.45 mm，泵供量W=2.28 g/min，空气段长度L=30 mm，喷丝头拉伸比λ=1.5。改变喷丝孔出口直径D0进行模拟计算。当泵供量不变时，意味着喷丝孔挤出速度v0将发生变化，为保证获得相同直径的初生纤维，本文设定一辊拉伸速度v1不变，从而改变喷头拉伸比。不同喷丝孔直径下的模拟结果如图5所示。

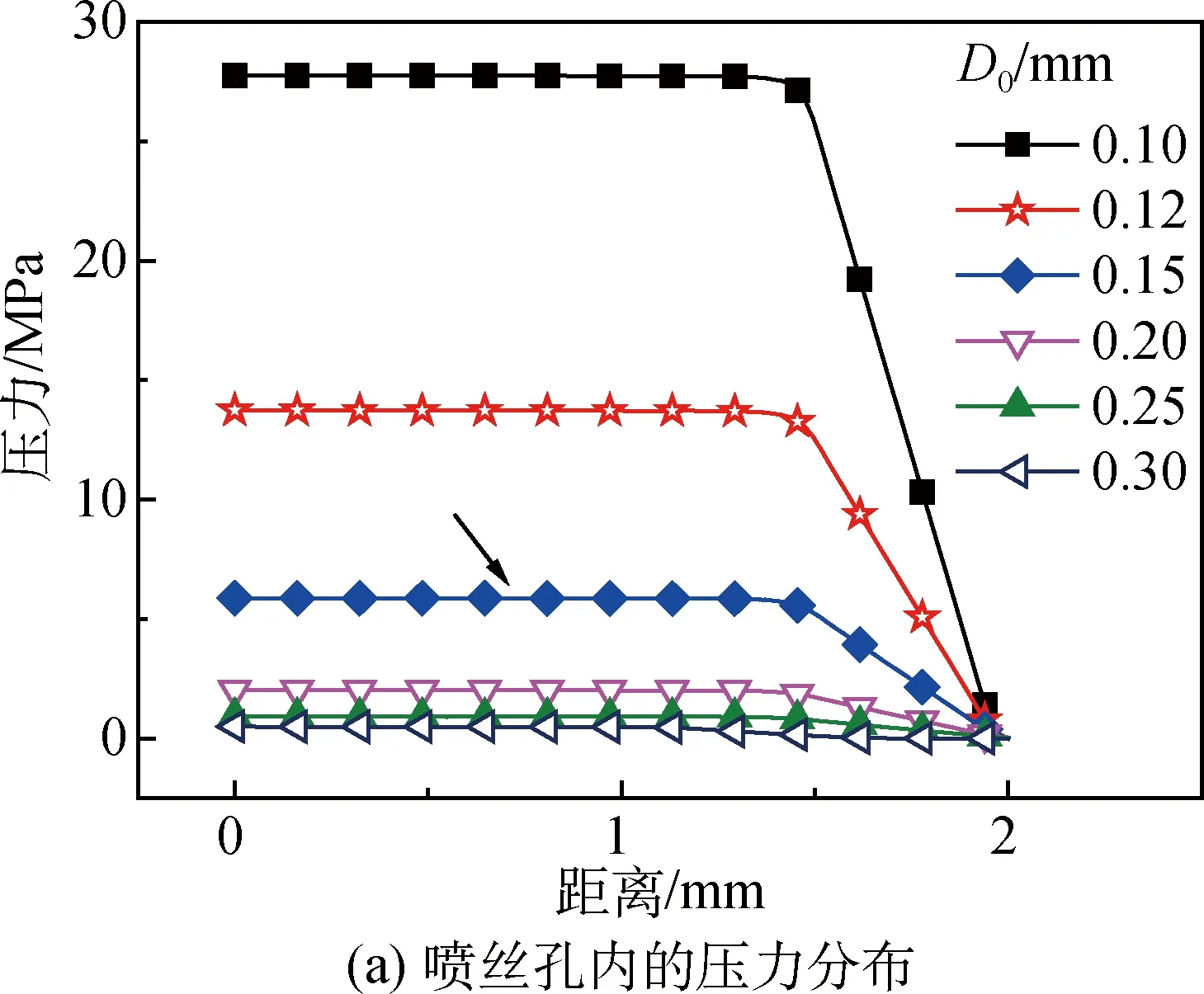
图5 不同喷丝孔直径下的模拟结果Fig. 5 Results under different spinneret outlet channel diameters

由图5(a)可知，箭头标记处为满足临界挤出可纺条件的板前压力，喷丝孔直径为0.15 mm。在相同的泵供量条件下，喷丝孔直径的变化会引起挤出速度的变化。当喷丝孔直径为0.10 mm时，板前压力过大(28 MPa左右)，挤出速度增大到6.9 m/min，纺丝过程中出现漏料现象，不能实现正常挤出；当喷丝孔直径为0.12 mm时，板前压力也较大(14 MPa左右)，挤出速度增大到4.8 m/min，溶液虽能正常挤出，但不能制备较细的PSA纤维，因为较大的挤出速度导致所需的后拉伸倍数过高。即要实现PSA/DMAc溶液干喷湿纺的正常挤出，只有选用更大的喷丝孔径。当喷丝孔径为0.15 mm时，溶液可以在较宽的纺丝温度和挤出速度范围内实现干喷湿纺的正常挤出。当喷丝孔直径在0.20 mm或以上时，板前压力不到3 MPa，可纺性较差，不适合进行纺丝试验。由图5(b)可知，增大喷丝孔直径，对丝条直径的影响较为显著，但是由于一辊拉伸速度不变，挤出速度的减小致使喷头拉伸比增大，而出口胀大比随孔径增大略微减小，但总体上变化不大。

3.3.2 喷丝孔长度(长径比)对溶液挤出的影响

设定PSA/DMAc溶液的参数：溶液温度T0=40 ℃，喷丝板入口直径D1=1 mm，出口直径D0=0.15 mm，入口角α=45°，泵供量W=2.28 g/min，空气段长度L=30 mm，喷丝头拉伸比λ=1.5。改变喷丝孔长度Ls进行模拟计算。不同喷丝孔长度下的模拟结果如图6所示。

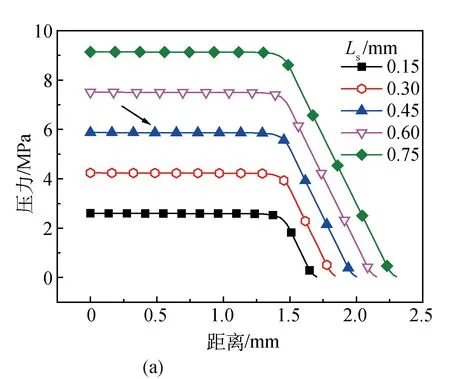
图6 不同喷丝孔长度下的模拟结果Fig. 6 Results under different spinneret outlet channel lengths

由图6(a)可知，板前压力受喷丝孔长度影响较为显著。喷丝孔长度为0.45 mm、入口压力约为6 MPa时，符合纺丝标准，溶液刚好能够挤出；当孔长度继续增大到0.60和0.75 mm时，入口压力分别为7.5和9.1 MPa，具有良好的可纺性，而喷丝孔长度小于0.45 mm时，入口压力太小，可纺性差。

由图6(b)可知，丝条的直径分布变化较小，其出口胀大比与喷丝孔长度成反比。出口胀大比公式[14]如式(11)所示，长径比越大，溶液在孔道中停留时间越长，更有利于分子链段弹性形变的松弛，丝条最大膨胀直径Dc减小，使得出口胀大比Qmax减小，从而减小了漫流发生的机率。因此，喷丝孔长度≥0.45 mm时，有利于溶液的顺利挤出。

(11)

3.4 纺丝工艺变化对PSA/DMAc溶液可纺性的影响

在喷丝板参数优化的基础上，模拟计算采用喷丝板入口直径D1=1 mm，出口直径D0=0.15 mm，喷丝孔长径比Ls∶D0=3∶1，入口角α=45°，纺丝溶液为PSA/DMAc。

3.4.1 纺丝温度对挤出动力学的影响

设计泵供量W=2.28 g/min，空气段环境温度Tamb=20 ℃，空气段长度L=30 mm，喷丝头拉伸比λ=1.5，改变纺丝温度进行模拟计算。不同纺丝温度下的模拟结果如图7所示。

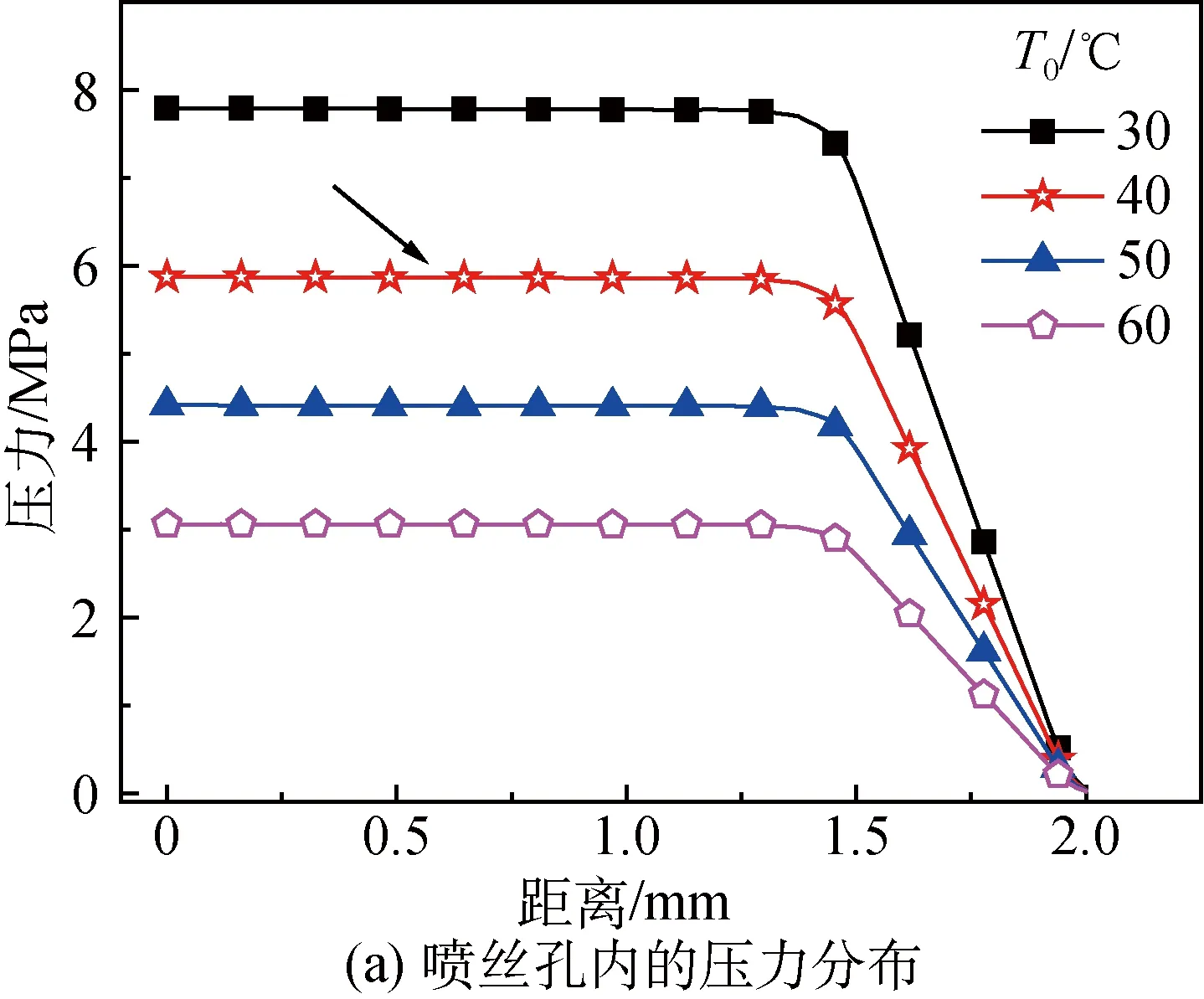
图7 不同纺丝温度下的模拟结果Fig.7 Results under different spinning temperatures

由图7(a)可知，纺丝温度的改变引起了明显的压力变化。可纺性纺丝结果表明，改变纺丝温度对溶液的黏弹性会产生较大的影响。因此，在其他条件不变的情况下，提高纺丝温度将使得溶液黏度下降，板前压力减小，可纺性较差，与试验过程中观察到的“漫板”现象相吻合，再次证明可纺性判据的合理性。纺丝温度为40 ℃时溶液能顺利挤出(标记处)，当温度为50和60 ℃时，板前压力不足，发生“漫板”现象。同时，温度为30 ℃时，压力提高到约8 MPa，理论上有利于可纺性，但试验过程中，由于溶液流动性较差，不易通过喷丝孔挤出，可纺性较差。这说明具有一定流动性的溶液才能适用于模拟计算。此外，纺丝温度对PSA丝条的直径分布有一定影响，而对出口胀大比的影响可以忽略。

由图7(c)和(d)可知，纺丝温度不同，沿纺程的丝条温度明显不同，而丝条速度、应力变化很小，说明纺丝温度对后续的拉伸影响并不显著。从图7(f)拉伸黏度的变化来看，纺丝温度降低，拉伸黏度有所增大，这将在一定程度上提高空气段丝条的可拉伸性。

3.4.2 挤出速度对动力学的影响

纺丝温度T0=40 ℃，空气段环境温度Tamb=20 ℃，空气段长度L=30 mm。在此条件下研究挤出速度(泵供量)变化对动力学的影响，为保持相同的喷头拉伸比(如λ=1.5)，同时改变一辊速度进行模拟计算，如图8所示。

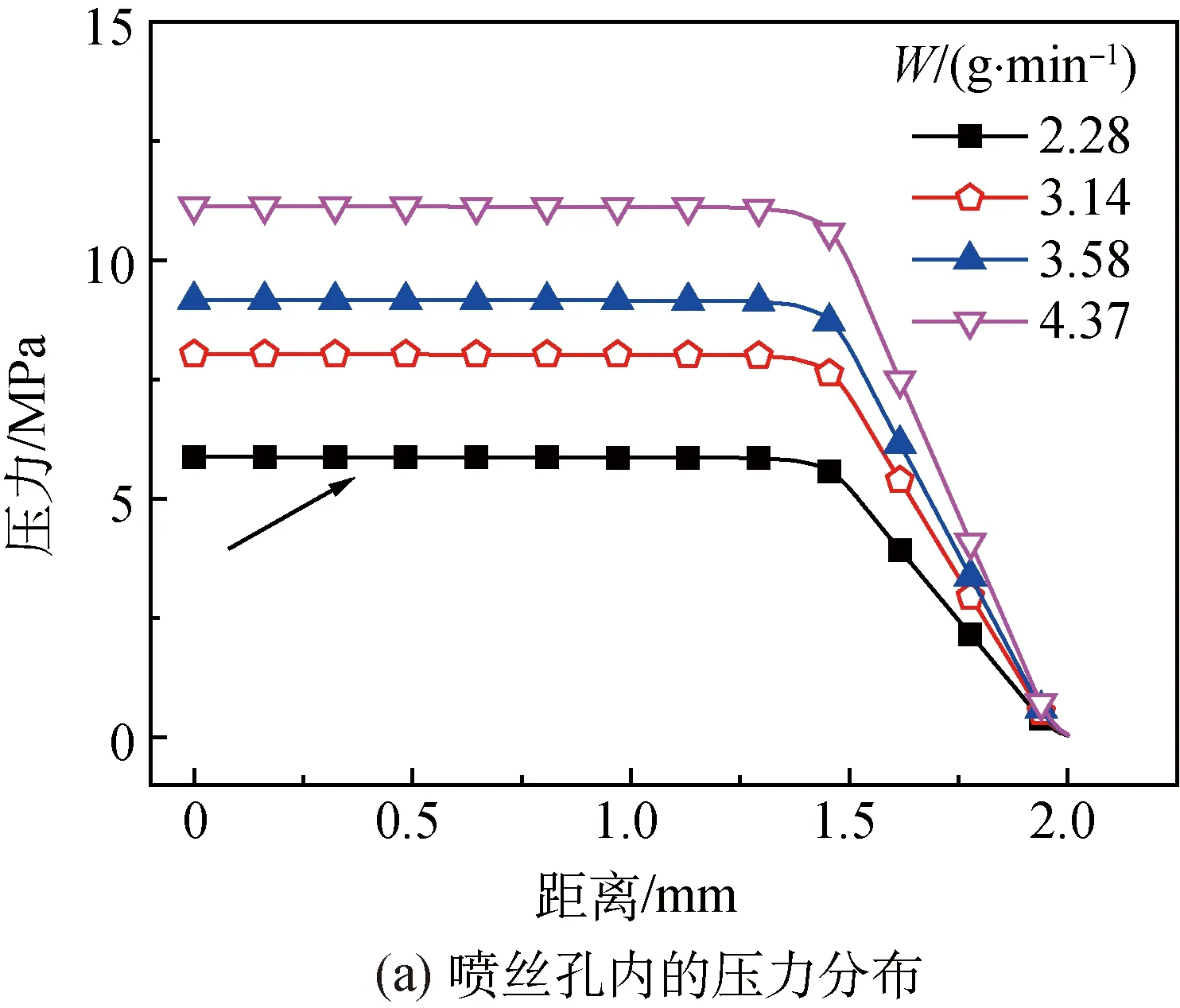
图8 不同挤出速度下的模拟结果Fig.8 Results under different spinning velocities

由图8(a)可知，增大丝条的挤出速度(同比改变相应倍数的一牵速度)，喷丝孔内压力显著增大，这是常用的通过提高挤出速度来提升可纺性的工艺调节方法。由于保持了喷头拉伸比不变，丝条直径的变化主要集中在喷丝孔出口挤出胀大区域，挤出速度增加，挤出胀大比明显减小(见图8(b))。这主要是因为挤出速度不同，导致丝条沿纺程的速度和应力变化不同(见图8(d)和(e))。增大纺丝速度，丝条运动速度更快，达到相同形变所需要的时间更短，喷丝孔中的剪切导致的分子链取向在挤出胀大阶段未来得及发生松弛，出口胀大比减小，有利于可纺性。同时由于丝条的冷却时间短，温度比较高，因速度增加产生的拉伸应力增大，综合结果导致拉伸黏度几乎不变(见图8(f))。

3.4.3 喷头拉伸比对挤出动力学的影响

模拟计算设定纺丝温度T0=40 ℃，泵供量W=2.28 g/min，空气段环境温度Tamb=20 ℃，空气段长度L=30 mm，改变喷头拉伸比λ进行模拟计算，结果如图9所示。

从图9可以看出，喷丝头拉伸比对喷丝孔内压力分布几乎没有影响，但丝条直径随拉伸比的变化而变化，且喷头拉伸比越大，越有利于得到更细的纤维，可效降低出口胀大比，减小漫流发生的几率。增大喷头拉伸比，由于丝条直径形变加快，形变速度大于其热交换速度，因此温度下降较慢，丝条温度较高。当喷头拉伸比为1.5倍时，丝条在挤出胀大后应力急剧下降，在10 mm左右的空气段后丝条的应力趋于稳定，根据干喷湿纺纺丝试验结果，此时得到的PSA凝胶丝条的取向和强度较低。当拉伸比继续增大时，应力在丝条挤出胀大后随拉伸比增大，PSA凝胶丝条的取向和强度明显提高。因此，在PSA纺丝过程中，喷头拉伸比应高于1.5倍，既有利于获得较高取向的PSA凝胶丝条，也有利于保证后续的拉伸以制备性能更好的纤维。

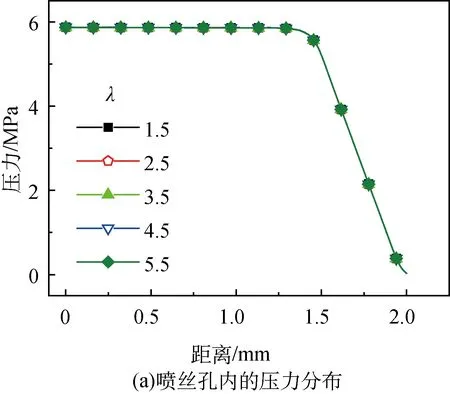
图9 不同喷头拉伸比的模拟结果Fig. 9 Results under different draw ratios

3.4.4 空气段长度对挤出动力学的影响

模拟计算设定纺丝温度T0=40 ℃，泵供量W=2.28 g/min，空气段环境温度Tamb=20 ℃，喷头拉伸比λ=1.5，改变空气段长度L进行模拟计算，结果如图10所示。

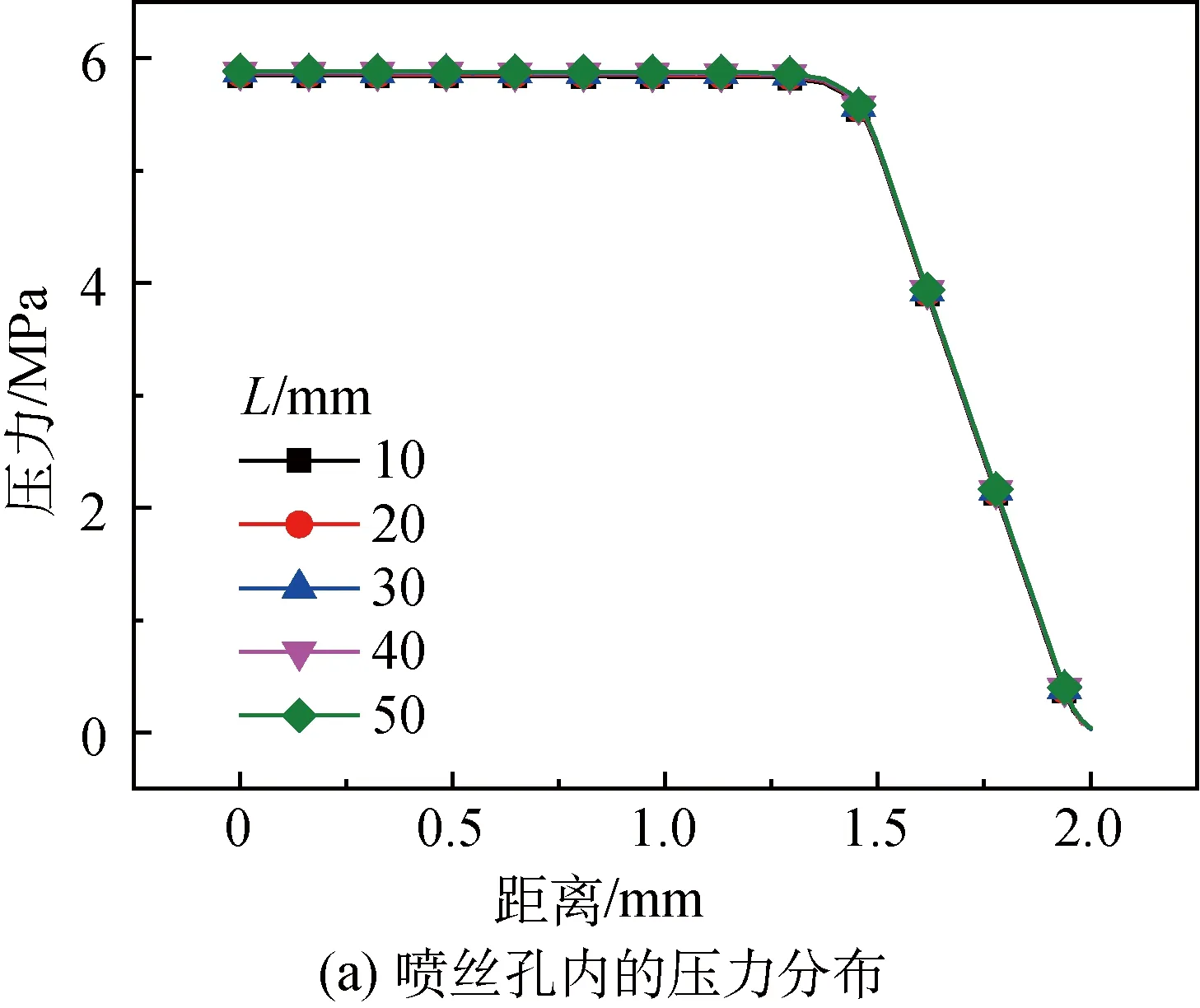
图10 不同空气段长度的模拟结果Fig.10 Results under different air gap lengths

由图10可知，空气段长度对喷丝孔内的压力分布几乎没有影响，但对丝条直径的形变和出口胀大比影响显著。丝条从喷丝孔挤出，发生挤出胀大，空气段长度为10 mm时，沿纺程的应力较高(见图10(e))，同时丝条速度迅速增大到拉伸速度(见图10(d))，速度梯度较大，直径迅速降低，出口胀大比较小，有利于可纺性。但考虑到分子链间的缠结，实际纺丝过程中丝条内链缠结部分不易拉伸，丝条快速形变能力与模拟结果可能会存在差异。空气段长度增大，丝条的速度增长较慢，沿纺程的应力逐渐减小，直径缓慢减小，出口胀大比较大，说明过大的空气段会增大漫流发生的概率。当空气段长度为40和50 mm时，纺程应力在挤出胀大后基本不发生变化，不利于丝条的取向增加，也不利于干喷湿纺的可纺性。

4 结 论

(1) PSA溶液在合适的喷丝孔径、纺丝温度和挤出速度条件下，具备干喷湿纺的可行性。通过干喷湿纺试验确定了PSA溶液具有良好可纺性的喷丝板微孔孔径和临界纺丝条件。结合测试得到的溶液参数，进行干喷湿纺动力学模拟计算，并通过结果分析，提出将板前压力和挤出胀大比作为评价干喷

湿纺可纺性的指标，满足PSA溶液可纺性的临界板前压力约为6 MPa，挤出胀大比小于1.5。

(2) 根据试验和模拟结果，结合可纺性判据发现，喷丝孔长度或直径变化会引起长径比的变化，适当增大喷丝孔长度或减小其直径有利于提高干喷湿纺的可纺性。因此，可以通过优化喷丝板设计来调节PSA溶液干喷湿纺可纺性。

(3) 在保证顺利纺丝的前提下，适当降低纺丝温度、增大泵供量可以避免发生漫流，而喷头拉伸比和空气段长度对PSA溶液干喷湿纺可纺性的影响较小，但对丝条空气段拉伸过程中的成形有显著影响。

此外，动力学模拟可以避免反复的试验，节约试错成本，提高生产效率。