植物叶片表面捕集气溶胶粒子特性数值分析

贾孟霞，付海明

(东华大学 环境科学与工程学院，上海 201620)

随着工业化、城市化进程加快，工业废气、汽车尾气、建筑粉尘的排放量显著增加，大气气溶胶粒子污染日益加剧，给人类的生产、生活带来巨大影响。在城市中合理种植绿色植物是降低粒子浓度较为经济有效的方式。宏观上，植物表现出一定的“滞尘”效应，即叶片可滞留并转移粒子；微观上，粒子通过布朗扩散、拦截、惯性碰撞及重力沉降等机理沉积在叶片表面，进而脱离大气环境[1-2]。因此，合理地预测植物叶片的滞尘效果及其影响因素对城市规划设计具有重要理论意义及实用价值。

针对植物“滞尘”现象的研究已有较多报道。一些学者主要通过现场测量的方式定量分析叶片捕集粒子的效果，例如：俞莉莉等[3]对扬州市绿色植物滞尘效益进行研究后发现，悬铃木等叶面越粗糙的植物捕集粒子的能力越强；赵松婷等[4]对北京市29种园林植物进行叶片采样，通过电镜分析评估粒子的滞留能力。另外一些学者重点关注了风洞试验及植物捕集粒子效率的参数化表达，例如：Chamberlain[5]对人工黏草沉积粒子进行风洞试验，提出将捕集效率作为衡量植物滞尘能力强弱的依据；Slinn[6]基于文献[5]的风洞试验数据对植物冠层的捕集效率进行拟合，得到了布朗扩散、拦截、惯性碰撞作用下粒子捕集效率的参数化表达式；Zhang等[7]指出空气湿度会影响粒子的沉积，并对不同品种植物的冠层捕集效率参数化表达式进行优化；Petroff等[8]对比了从森林、草地上测得的粒子沉积数据与现有的参数化模型模拟数据，结果表明参数化模型具有一定优越性；Zhang等[9]基于颗粒动力学分析方法进行风洞试验，测量了植物表面粒子的沉积速度，结果表明沉积效率受粒子粒径和风速的影响。

综上所述，现有研究主要集中在宏观层面下植物捕集粒子的效率预测及影响因素探究方面，而鲜有关于微观尺度下单个植物叶片对粒子捕集行为影响的研究报道。本文在相似理论基础上采用拉格朗日法追踪粒子的运动轨迹，并在微观尺度下研究植物单叶片表面对微细粒子的捕集效率，探究粒子粒径、风速和迎风角对叶片捕集效率的影响，并尝试给出叶片捕集粒子的效率表达式，以期为植物改善城市空气质量环境提供理论参考。

1 物理问题及研究方法

1.1 流场模型

植物叶片的形状多种多样，本文选择较为常见的扁平形叶片，将其置于长方体流场中，假设风向垂直于叶片。鉴于三维流场的运算较为复杂，截取植物叶片所在的xy平面将流场简化为二维。植物叶片捕集粒子的流场及计算域如图1所示，其中，叶片厚度为0.5 cm，长度l为20 cm。基于l对叶片中心与计算域边界间的距离进行无量纲处理，得到叶片中心与速度入口的距离为4l，与压力出口的距离为8.5l，与上、下边界的距离均为3.75l。迎风角θ为叶片中线与水平轴x轴的夹角。

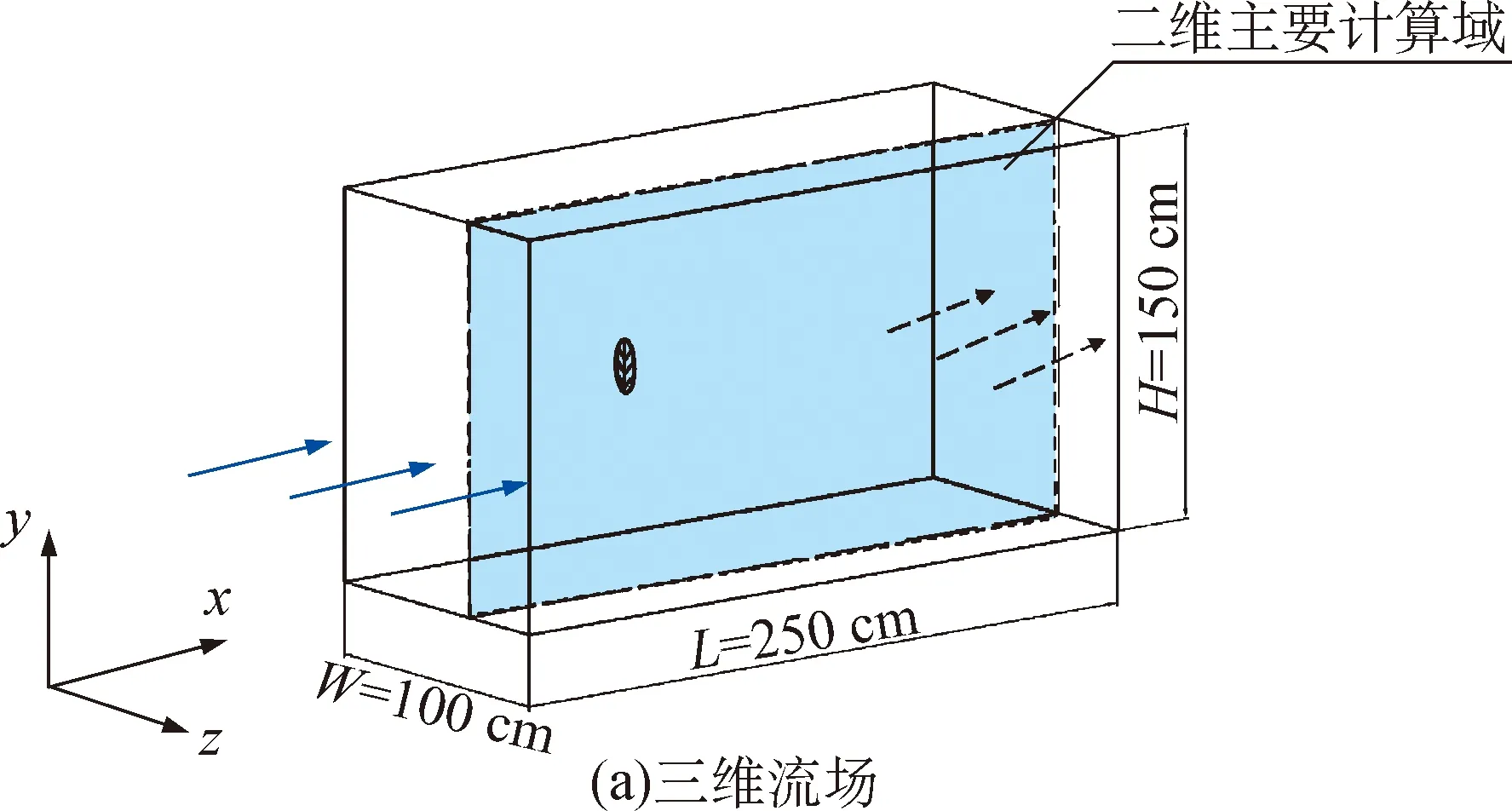
图1 植物叶片捕集粒子的流场及计算域Fig.1 Flow field and computational field of plant leaf capture particles

根据植物叶片的长度l、风速v以及运动黏度μ计算雷诺数Re可知，流场中空气的运动处于紊流状态。为简化计算，假设其为二维定常不可压缩流动，满足的连续性方程和Navier-Stokes方程如式(1)～(3)[10]所示。

(1)

(2)

(3)

式中：vx、vy分别为x、y轴方向的流体速度分量，m/s；μ为空气动力学黏度，Pa·s；ρ为空气密度，kg/m3；p为空气压强，Pa。

由于叶片、流场的尺寸与粒子粒径的数量级相差较大，在Fluent软件中求解流场时，若网格划分尺寸过小则计算机无法求解，故将叶片及计算流域原型尺寸缩小到1/1 000，即ln/lm=1 000，下标n、m分别代表原型和模型，此时称原型和模型具有相似性，即在对应的时空点，标量的特征尺寸大小成比例，矢量速度大小成比例、方向相同[11-12]，并且满足Stkn=Stkm，斯托克斯数计算式如(4)所示。

(4)

式中：Stk为斯托克斯数，其描述粒子惯性作用与扩散作用相对大小；ρp为粒子密度，kg/m3；dp为粒子直径，m；μ为空气动力学黏度，Pa·s；v为风速，m/s；l为叶片长度，m。由式(4)可以得到如式(5)所示的规律。

(5)

为得到更为精确的流场和粒子轨迹，在ICEM CFD软件中对模型流域进行网格划分，同时在树叶周围进行局部加密处理，并进行网格无关化验证。在Fluent软件中应用式(1)～(3)求解流体运动方程，边界条件设置如下：入口采用速度入口，上、下边界设置为对称边界条件，出口设置为压力出口，壁面采用无滑移边界条件[13]，压力速度耦合计算采用Simple算法。

1.2 粒子运动轨迹方程及求解

描述流体运动的方法有两种：欧拉法和拉格朗日法。拉格朗日法是指以某一个流体质点的运动为研究对象，观察这一质点的运动参数(位置、速度、加速度等)随时间的变化规律。本文描述粒子的运动采用拉格朗日法，将粒子视为离散相，观察其运动轨迹。当粒径dp<0.1 μm时，粒子悬浮在空气中易受到空气分子的无规律撞击，从而产生随机不定向运动即布朗运动，此时主要受布朗随机力的影响。随着粒径的增大，布朗扩散作用逐渐减弱，而惯性作用加强，此时颗粒物受到流体的斯托克斯阻力。空气

中粒子浓度较低时，可忽略粒子间的相互作用力，则单个粒子的无规则Langevin运动轨迹方程可描述为式(6)[14-16]。

(6)

粒子所受斯托克斯阻力[17]可表示为

(7)

式中：ex、ey分别为x和y轴方向的单位矢量；C为Cunningham修正系数，C=1+Kn[1.257+0.4exp(-1.1/Kn)]，Kn为粒子的克努森数。

粒子所受布朗随机力[18]可表示为

(8)

式中：ζx、ζy为单位变量独立高斯随机数；Δt为时间步长，取粒子的弛豫时间，s；T为热力学温度，K；κB为玻尔兹曼常数，κB=1.38×10-23J/K；D为粒子扩散系数。

1.3 粒子的捕集效率

采用统计学方法计算叶片捕集粒子的效率[19]，如式(9)所示。

(9)

式中：E为模拟捕集效率均值；NG为粒子发射数；NC为粒子捕集数；HG为粒子释放面高度，m；rl为树叶的垂直方向投影长度，rl=lsinθ，m。

2 结果与讨论

利用Fluent 16.0软件对植物捕集粒子模型进行求解。为讨论不同机理下粒子的捕集效率，模拟中气溶胶粒子需包含布朗扩散起主导作用的超细微粒(dp<0.1 μm)、拦截能力较强的亚微米级粒子(0.1～1.0 μm)、惯性碰撞起主导作用的微米级粒子(1～50 μm)、重力沉降起主导作用的超大粒子(>50 μm)[20]。为讨论风速v和迎风角θ对捕集效率及粒子分布的影响，设计参数如表1所示。

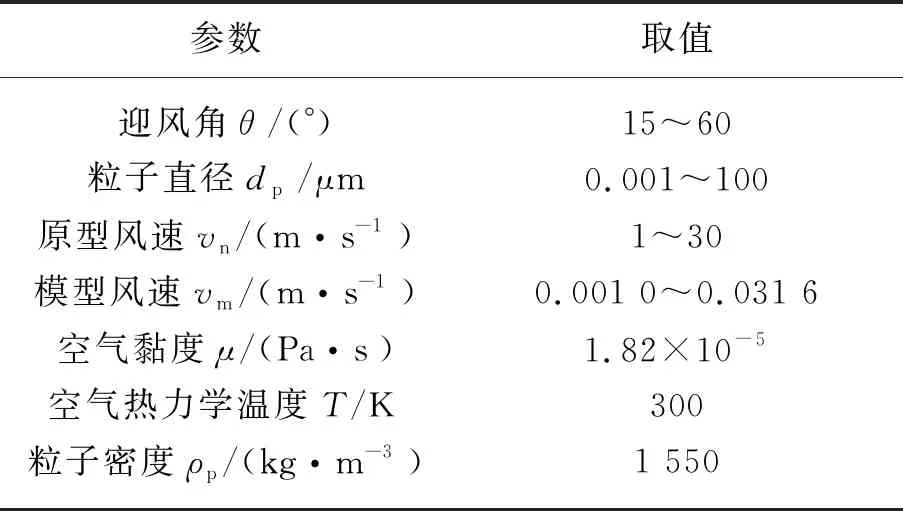
表1 模型主要设计参数Table 1 The main design parameters of the model

2.1 粒子绕叶片表面运动的轨迹特征

为便于观察，令叶片位于尺寸为0.010 m×0.006 m平面的中心，如图2中4条虚线汇聚所成的虚线框所示。考虑到我国北方地区近50年来平均风速为2.71 m/s[21]，选取vn=3 m/s；同时为观察布朗扩散、惯性碰撞机理下粒子的运动，分别选择超细微粒(dp=0.005 μm)、微米级粒子(dp=5.000 μm)，绘制此时不同迎风角(θ=15°、30°、45°、60°)下的粒子运动轨迹图如图3所示，其中灰色线条为叶片表面绕流流线。

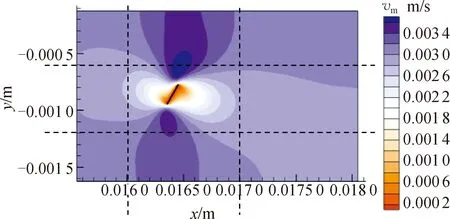
图2 粒子在叶片表面绕流的研究区域Fig.2 The main region of particles around the blade surface

由图3可知，空气在不同迎风角的叶片表面发生绕流，导致流线发生偏转，粒子的运动轨迹也相应发生变化。当粒径为0.005 μm时，粒子受到的各方向空气分子撞击作用不平衡，表现出无规则的运动轨迹，即布朗运动，此时扩散机理占据主导地位；随着粒径的增大(dp=5.000 μm)，粒子运动变得较为规律，当气流经过叶片表面发生偏转时，粒子由于惯性作用的增强，不能完全跟随空气分子及时避开叶片，导致发生碰撞的粒子被叶片表面所捕集[22]，遵循惯性碰撞捕集机理。

图3 植物叶片绕流流场分布及粒子轨迹(vn=3 m/s)Fig.3 Orbital flow field distribution and particle trajectory of plant leaves (vn=3 m/s)

2.2 风速对叶片捕集粒子的影响

不同迎风角下，捕集效率随风速表现出一致的规律性，选择迎风角θ=60°，绘制不同风速下叶片的捕集效率，如图4所示。由图4可知，捕集效率随粒径的增大呈先减小再增大的趋势。对于粒径较小(dp<0.1 μm)的粒子，捕集效率随风速的增大而减小，下降趋势由急速变为平缓；对于粒径为0.1～1.0 μm的粒子，捕集效率无明显变化趋势；对于粒径dp>1.0 μm的粒子，捕集效率随风速的增大而增大。由图4(b)可知，随着风速的增大，捕集效率由下降转变为上升所对应的粒径逐渐减小。

图4 捕集效率与粒径和风速的关系Fig.4 Relationship between capture efficiency and particle sizes/wind speeds

2.3 迎风角对捕集效率的影响

现实生活中植物叶片通常呈多种不规律角度，迎风角对捕集效率的影响尚待讨论，通过微观尺度定性分析其对捕集效率的影响，可为日后研究整株植物不同迎风角下的捕集效率奠定基础。选取风速vn=5 m/s，将不同迎风角下叶片的捕集效率绘制成图5。由图5可知，不同迎风角时的捕集效率之间无显著差异。在迎风角低于90°条件下，当粒径dp<1.0 μm时，布朗扩散捕集效率随迎风角的增大而减小，随粒径的进一步增大，捕集效率也随之增大。

图5 捕集效率与粒径和迎风角的关系Fig.5 Relationship between capture efficiency and particle sizes/windward angles

2.4 捕集效率公式拟合

根据粒子沉积机理，分段阐述捕集效率，即布朗扩散效率EB和惯性碰撞效率Eimp。布朗运动中采用扩散系数刻画粒子的运动快慢[23]，引入施密特数Sc描述粒子的动量扩散与质量扩散，如式(10)[23]所示。随着粒径的增大，惯性作用加强，采用斯托克斯数Stk描述粒子的运动，如式(4)所示。Stk越大，颗粒与气体流线的重合率越小，即颗粒抵抗跟随气体流线流动的能力增强[24]。

(10)

式中：a为20 ℃时的空气运动黏度，m2/s；D为布朗扩散系数，m2/s。

2.4.1 布朗扩散效率的拟合

采用Origin 9.0软件将不同风速、粒径、迎风角下布朗扩散效率EB的数据拟合成施密特数Sc、迎风角θ及风速v的公式，如式(11)所示。

EB=1.219sinθ-0.139Sc-0.547v-0.467

(11)

式中：θ为弧度制迎风角。

将CFD模拟得到的捕集效率数据与拟合得到的布朗扩散效率EB绘制成图6，图中散点为模拟所得数据，曲线为拟合结果。由图6可知：6条彼此不重合的曲线代表不同风速下的捕集效率，曲线斜率随风速的增大而减小；在相同风速下，不同迎风角的捕集效率曲线出现一定程度的重合，进一步表明迎风角对布朗扩散捕集效率的影响甚微。此外，当Sc<105即粒径dp<0.3 μm时，拟合结果与模拟结果吻合度较高，相关系数r=0.99，对于小粒径的粒子，捕集效率随Sc的增大呈规律性递减，随风速的增大而减小。

图6 布朗扩散捕集效率拟合与模拟数据验证Fig.6 Brownian diffusion capture efficiency fitting and simulation data verification

2.4.2 惯性碰撞效率的拟合

微米级粒子在被叶片捕集时，惯性碰撞起主导作用，故选择粒径尺寸dp>1 μm时模拟得到的捕集效率，与斯托克斯数、风速、迎风角进行拟合，得到惯性捕集效率Eimp的表达式，如式(12)所示。

(12)

将模拟所得数据与拟合公式所得计算结果绘制成图7。由图7可知，当Stk>10-5时，即对应粒径(dp>1 μm)拟合所得结果与模拟数据的相关性较好，r=0.97。由图7可知：在锐角范围内，迎风角的增大促使捕集效率Eimp增大，这可能是因为增大迎风角度将使得叶片作为障碍物的捕集面积增大；对于微米级粒子，Eimp随着Stk的增加而增大。

图7 惯性碰撞捕集效率拟合与模拟数据验证Fig.7 Inertia collision capture efficiency fitting and simulation data verification

2.4.3 总效率的拟合结果

依据经典过滤理论[25]，定义植物叶片捕集粒子的总效率E=EB+Eimp，如式(13)所示。

E=1.219sinθ-0.139Sc-0.547v-0.467+

(13)

将拟合结果与模拟所得结果绘制成图8。由图8可知，粒径为0.1～1.0 μm时拟合结果与模拟结果差异较大，这可能是因为拟合时忽略了拦截作用所造成的粒子捕集。总体而言，拟合结果与模拟结果的吻合度较高。

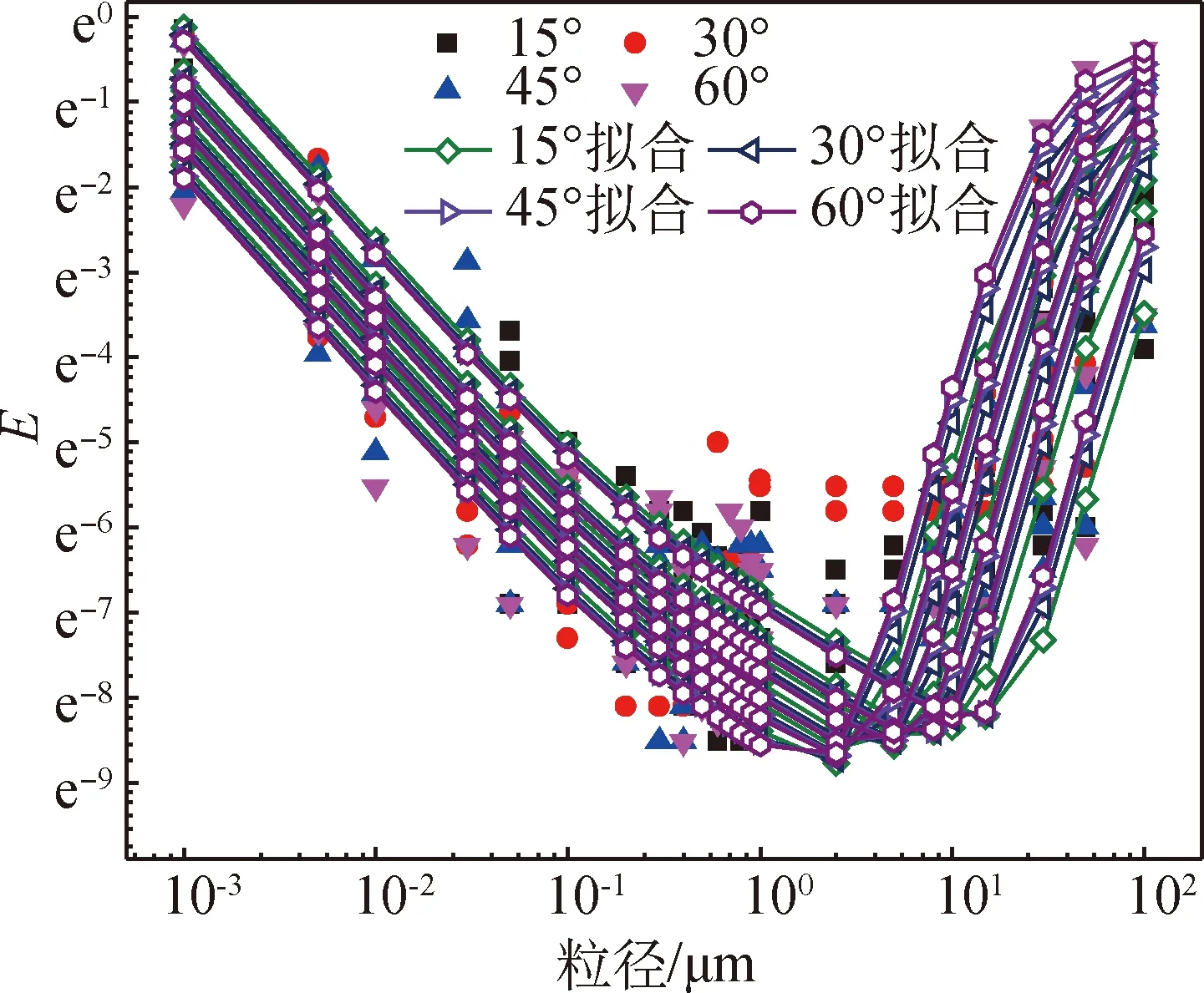
图8 总效率拟合与模拟数据验证Fig.8 Verification between the total efficiency of the fit and the simulated data

2.5 植物单叶片捕集总效率预测公式的验证

文献中布朗扩散、惯性碰撞及总效率的参数化表达式如式(14)～(16)所示。

(14)

(15)

(16)

式中：Ea为文献总效率；EBa为文献[6]的布朗扩散效率；Eimpa为文献[7]的惯性碰撞效率；cv/cd为黏性阻力比，取0.3；γ为经验常数，植物表面取值为0.67；α为经验常数，与植被冠层种类有关，取混合阔叶树和针叶树所对应的参数值0.8。

文献[6-7]中研究条件均是风向垂直于叶片，故式(11)～(13)中迎风角度取90°，其余参数取值如表1所示，将计算得到的布朗扩散、惯性碰撞以及总捕集效率分别与文献结果进行对比，如图9～11所示。由图9可知，对于小粒径(dp<1.0 μm对应Sc<105)粒子而言，拟合结果与文献结果的变化趋势基本一致，本文EB的拟合结果为多条斜率的曲线，而文献[6]仅有1条曲线。这是由于本文将风速这一影响因素考虑进去，由拟合公式可知，斜率越大风速越小。由图10可知，对于大粒径(dp>1.0 μm对应Stk>10-5)粒子而言，Eimp拟合结果与文献值的整体变化趋势一致且吻合度较高，说明本文提出的方法具有可行性。由图11可知，总效率E的拟合与文献结果变化趋势一致，但在粒径处于0.1～1.0 μm时，拟合结果的值存在过高估计的现象，这可能时由于本文没有考虑粒子的拦截作用。

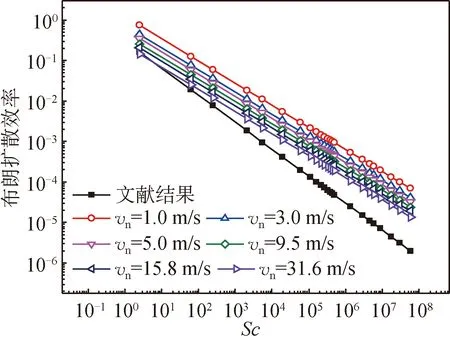
图9 布朗扩散效率的拟合结果与文献结果Fig.9 Fitting results and literature results of Brownian diffusion efficiency

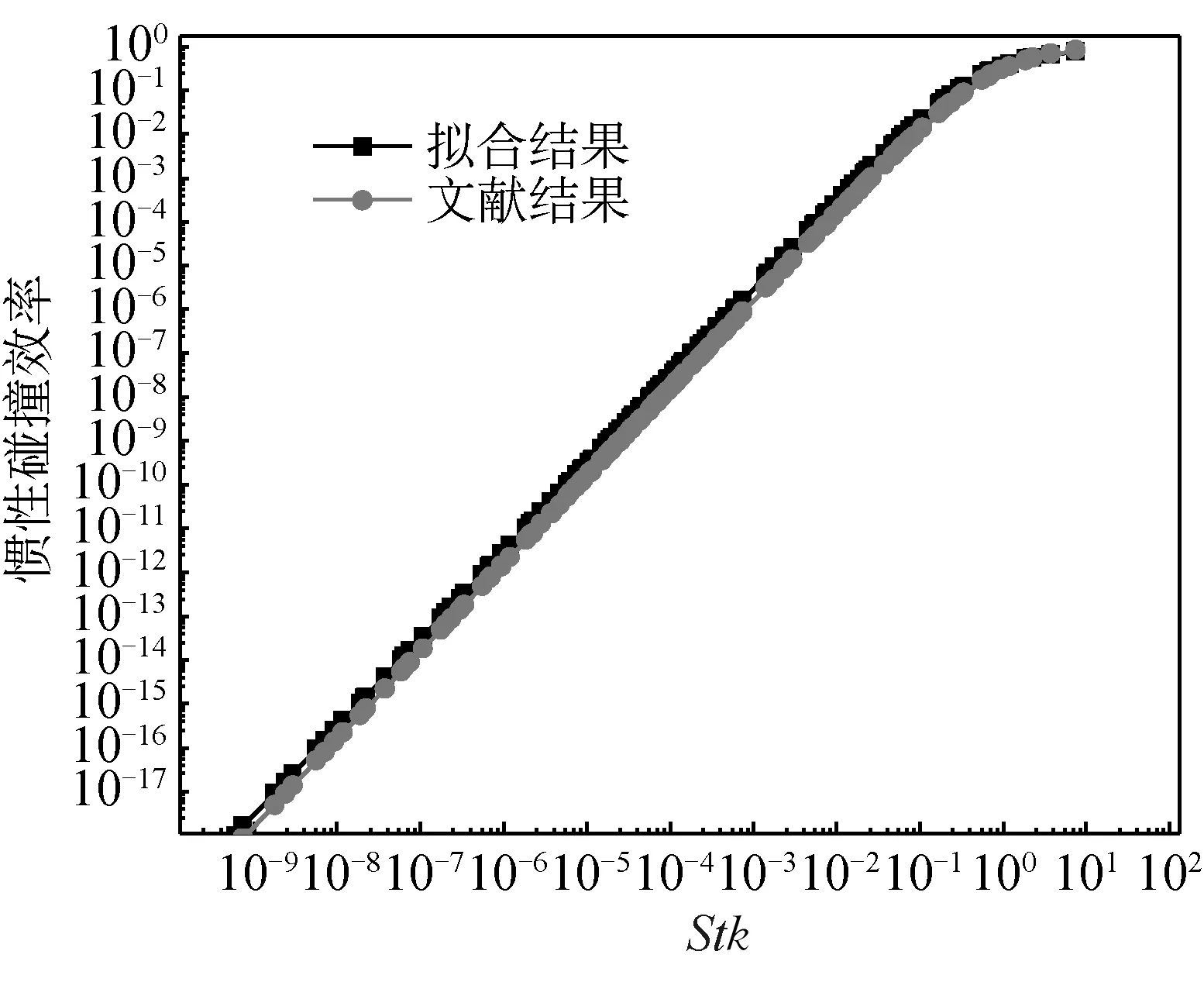
图10 惯性碰撞效率的拟合结果与文献结果Fig.10 Fitting results and literature results of inertia collision efficiency

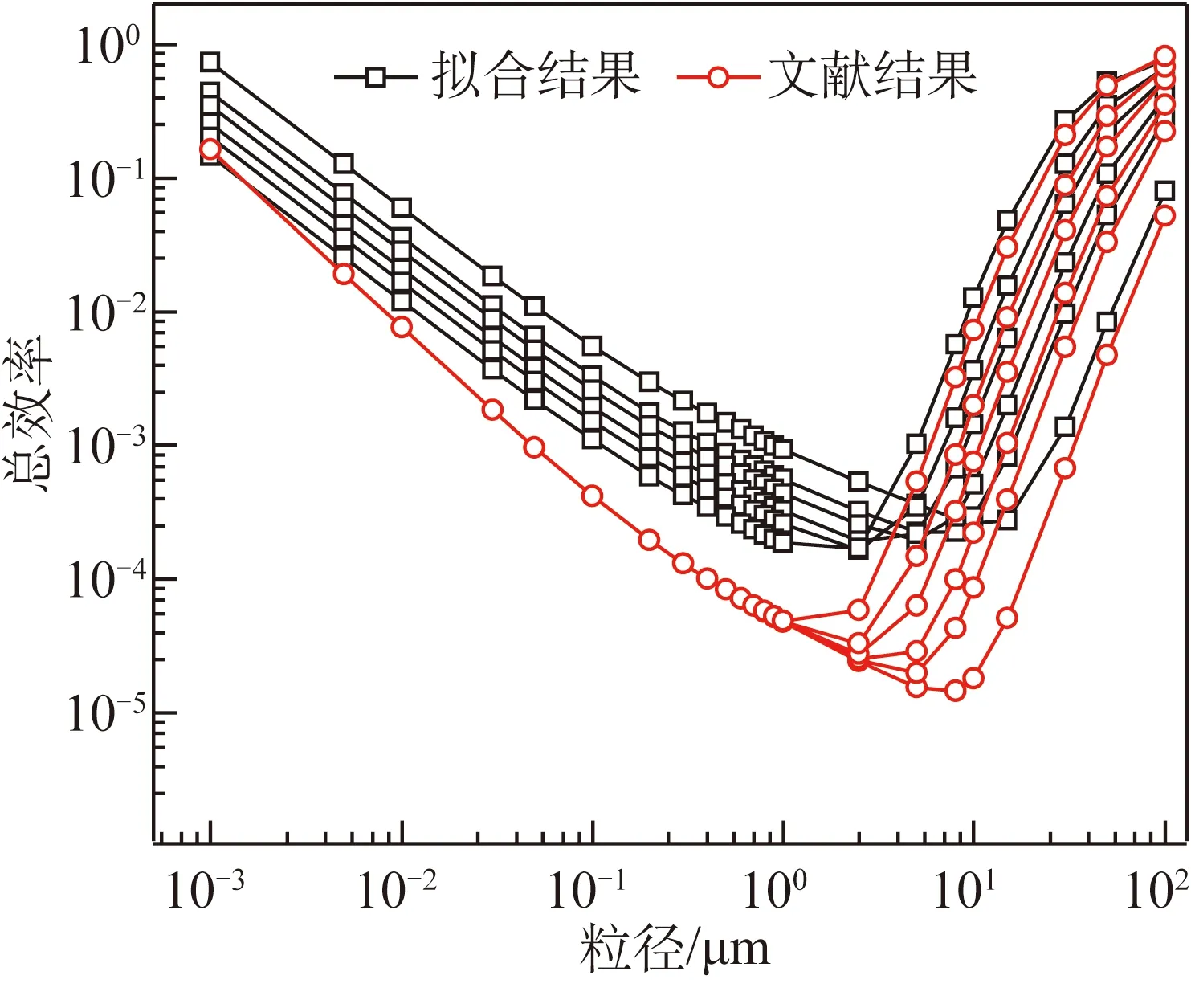
图11 总效率的拟合结果与文献结果Fig.11 Fitting results and literature results of total efficiency

3 结 语

本文针对植物叶片捕集粒子的物理现象，应用物理模型相似理论及数值分析法求解植物叶片表面附近的流场，同时考虑粒子布朗扩散和惯性碰撞的联合作用，应用拉格朗日法追踪粒子运动轨迹并求解植物叶片表面粒子捕集行为。分析计算得到捕集效率，讨论了粒径dp、迎风角度θ、风速v对捕集效率的影响，同时对效率与施密特数Sc、斯托克斯数Stk进行拟合得到效率的预测式，通过与文献进行对比，得到以下结论：

(1) 随着粒径的增大，捕集效率呈先减小后增大的趋势，这与叶片捕集粒子的机理相关。粒径较小时粒子的布朗扩散起主导作用，随着粒径的增大，惯性作用增强，惯性碰撞起主导作用。

(2) 对于dp<1.0 μm的粒子，迎风角度对捕集效率的影响很小，随迎风角的增大，捕集效率呈下降趋势；对于dp>1.0 μm的粒子，迎风角度θ的影响显而易见，随着迎风角的增大，叶片捕集的粒子数也呈现增加趋势。

(3) 当粒径dp<0.1 μm时，捕集效率随风速的增大而降低；当粒径在0.1～1.0 μm时，捕集效率随风速变化不明显；当dp>1.0 μm时，捕集效率与风速呈正相关。

(4) 根据不同的捕集机理分别拟合出布朗扩散、惯性碰撞作用下捕集效率公式，应用叠加原理得到总效率预测公式。本文中捕集效率随粒径的整体变化趋势与文献研究结果较吻合，但在粒径为0.1～1.0 μm时，本文应用预测公式计算所得的总效率偏大。