基于CatBoost算法的硕士研究生就业能力预测模型

巩 红，陈 阳，周晨晖，李昊楠，喻小康

(1.西安邮电大学 研究生院，陕西 西安 710121；2.西安邮电大学 经济与管理学院，陕西 西安 710121； 3.西安邮电大学 马克思主义学院，陕西 西安 710121)

随着硕士研究生招生规模的扩大，中国已经成为研究生教育大国[1]。毕业研究生人数不断攀升，就业问题也日渐受到重视。在硕士研究生就业预测的研究中，国内研究者大多使用传统的回归方法构建就业能力预测模型，但此方法在构建非线性的模型时难以精确预测。因此，构建一个能够准确预测硕士研究生就业能力的模型显得十分重要。

近年来，学界关于硕士研究生个体就业能力影响因素的研究主要分为探究高校对就业的影响和探究硕士研究生个体特征对就业能力的影响两类。高校对硕士研究生就业能力的影响是多方面的，文献[2]发现双一流建设高校的本科学历对所有层次的硕士研究生的就业满意度均有积极影响。但是，在起薪方面，硕士研究生的本科学历仅对双一流高校硕士研究生有正向作用。另有研究表明，硕士研究生的培养目标与就业需求的不匹配是导致研究生就业难的重要因素之一[3]。硕士研究生的个体特征对就业能力的影响因素主要包括先赋性因素[4-6]和研究生在硕士阶段学习获得的能力、成果和学习经历等后致性因素[7-8]。

目前,主要使用逻辑回归算法构建硕士研究生的就业模型。孙怡帆等[9]使用Lasso-Logisitic算法构建毕业生去向预测模型。王立非等[10]运用线性回归分析探究家庭背景、本科背景、生源地等与就业单位类型的关系。

随着机器学习的日益完善，国内外均有研究者使用机器学习算法研究研究生就业问题。Bowers在利用相对操作特征(Relative Operating Characteristic，ROC)分析学生各项辍学指标对其辍学行为进行预测[11]。Oztekin构建了一个集成毕业生毕业预测模型，选择30项教育数据预测学生是否顺利毕业[12]。Qu[13]等通过多层感知器构建学生就业预测模型。国内也有许多研究者对此进行研究[14-16],分别提出了基于遗传神经网络的学生成绩预测方法、集成学习方法并用其构建学生成绩预测模型及构建了基于最邻近规则分类(K-Nearest Neighbors,KNN)算法的分类预测模型。

现有的研究多从不同的角度探究硕士研究生就业能力影响因素问题，但多从单个视角出发进行研究，针对硕士研究生培养过程以及客观数据的研究相对较少，并且模型指标数目较少。在研究方法方面，构建模型时，未预先对数据分布问题进行处理，导致最终结果可信度不足。因此，为了更加深入地分析硕士研究生就业能力的影响因素，预测硕士毕业生的就业能力，拟构建一种基于CatBoost算法的研究生就业能力模型。采用SMOTE过采样方法处理数据集的不平衡问题以防止后续模型产生偏差。将该算法与其他算法进行对比分析，验证基于该算法的硕士研究生就业能力模型的预测效果，并对影响硕士研究生就业能力的影响因素进行分析。

1 指标选取与数据预处理

1.1 指标选取

考虑影响硕士研究生就业能力的主要因素，设定了科研训练、实践训练及学位论文训练等4个一级指标和科研项目、期刊论文及创新基金等10个二级指标，具体的指标及指标内容如表1所示。

表1 硕士研究生培养过程中的指标设置

1.2 数据预处理

1.2.1 指标测量

将收集到的原始数据集分为分类型和赋值型变量两类，具体分类型变量分类标准和连续型变量赋值标准分别如表2和表3所示。

表2 分类型变量分类标准

表3 连续型变量赋值标准

通过计算峰度、偏度指标进行检验，所采集的数据近似服从正态分布，对于少量输入项缺失的样本采用平均值填补样本的缺失值。

1.2.2 数据标准化

考虑变量具有种类多、量纲多和量纲差异大的特点，将对收集到的数据进行Z-score标准化处理。经过标准化处理的数据可以使不同类型特征变量的量纲相同，能处理防止由于单个变量量纲过大从而造成结果精度损失的情况发生。变量的具体转化公式[9]为

(1)

1.2.3 SMOTE过采样

在所收集的数据集中，未就业硕士研究生样本远少于就业硕士研究生样本，导致样本数据分布不均匀。若直接使用该类数据集对预测模型进行训练，会使输出结果偏向于占比较大的类别样本，影响到模型的计算准确性。因此，采用SMOTE过采样方法，在不改变该类样本总体特征的前提下，直接对占比较少的类别样本按照特定规律增加其数量，便于模型构建。

对于少数类中每一个样本δ，以欧氏距离为标准计算其到少数类样本集中所有样本的距离，得到其k近邻。首先，根据样本不平衡比例设置一个采样比例以确定采样倍率N。其次，对于每一个少数类样本δ，从其近邻中随机选择若干个样本，假设选择的近邻为o。最后，对于每一个随机选出的近邻分别与原样本构建新的样本[17]，新样本的表达式为

T=o+rand(0,1)(x-0)

式中，rand(0,1)表示0到1的随机数。

由此可以产生多个新的样本，且新的样本仍然具有原样本的基本特征。采用SMOTE过采样方法，将未就业研究生样本的数量扩充，与就业研究生样本数量持平。

2 模型构建

2.1 就业预测模型构建

将机器学习方法运用到高校就业的工作中，用于挖掘学生个人培养数据与就业之间的关系，进一步建立就业能力预测模型。首先，将原始数据集进行数值化、缺失值填充和标准化等数据预处理。其次，对数据集进行SMOTE过采样，从而消除数据集样本的不平衡问题。进而将数据集划分为训练集和测试集，再利用10倍交叉验证将所得训练集不断划分，充分训练CatBoost模型。最后，使用测试集验证CatBoost训练模型的有效性。硕士研究生就业能力预测建模具体过程如图1所示。

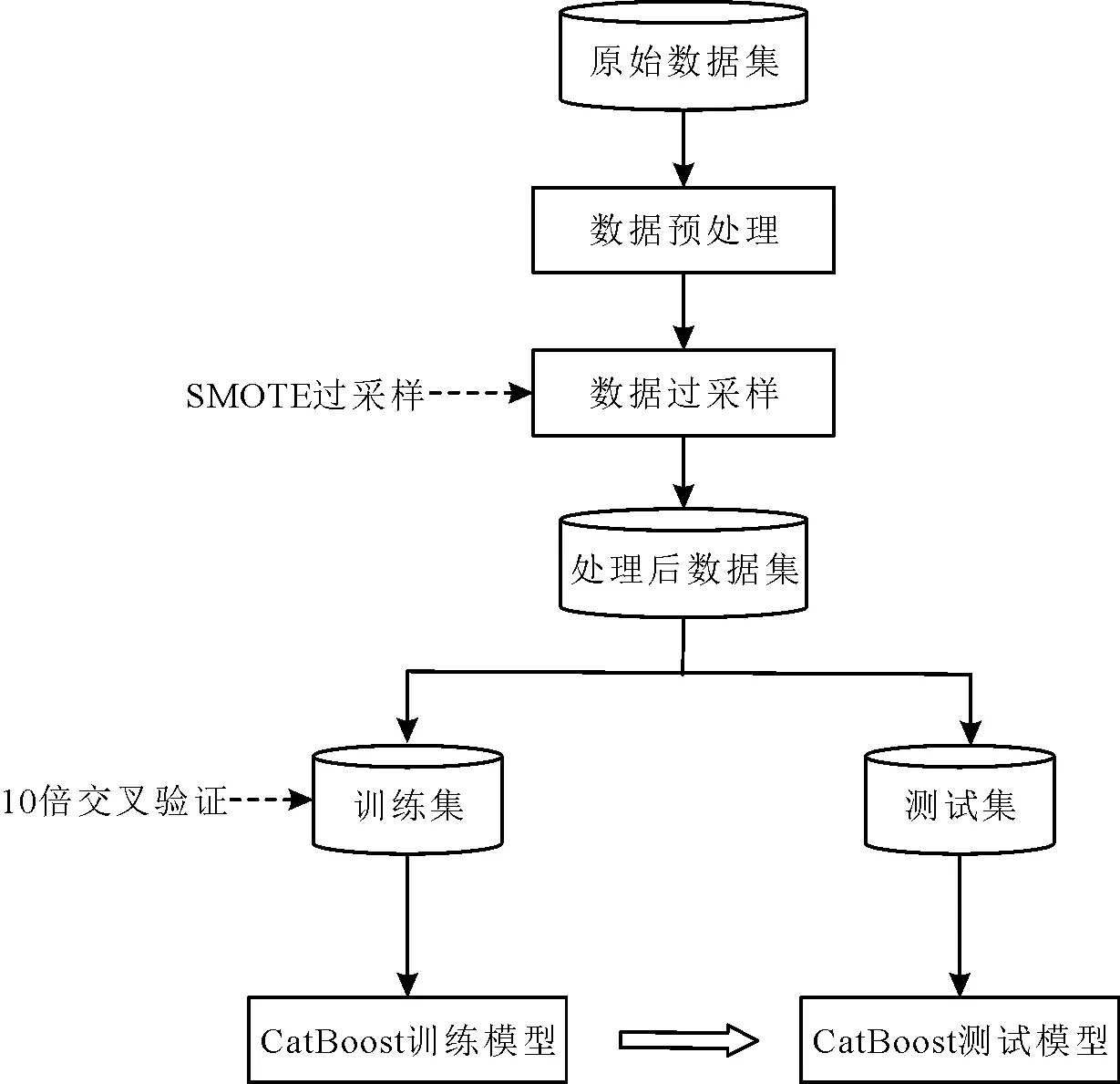
图1 就业能力预测建模过程

2.2 CatBoost算法

考虑CatBoost算法[17]在高效合理地处理类别特征、进行特征组合、丰富特征维度及克服梯度偏差方面具有一定优越性，在处理特征较多且分布不均匀的硕士研究生就业数据方面具有相对优势。因此，通过CatBoost算法对硕士研究生培养及就业数据进行预测模型的构建。

2.2.1 类别特征处理

由于研究中存在一些取值较多的特征变量，如果使用目前使用广泛的one-hot方法进行处理，会产生大量新的特征，最终导致计算量过大。因此，Catboost算法采用目标变量统计方法处理类别特征，该算法能够减少计算量以及降低信息损失程度。具体步骤如下。

步骤1设S为样本总数据集，Xi为样本类别特征向量，表达式分别为

式中：Y为样本的标签值；x为样本的类别特征；m表示样本类别特征总数；n为样本总数。

(3) 试验初期，排水管壁面积的大小会影响土体梯度比Gr值下降速度。与小直径排水管壁试样相比，在大直径试样条件下，砾质黏性土下降速度变缓的时间比小直径试样早3 h，砂质黏性土早3 h，粉质黏性土早1 h。梯度比下降速度大小为：大直径排水管壁试样>小直径排水管壁试样。

步骤2将所有样本随机排列，生成多个随机序列。

步骤3针对某个序列，用训练数据集的平均标签值替换类别，第i个样本中的第k个特征标签值计算公式为

(1)

式中：若xjk=xik，则[xjk=xik]=1；若xjk≠xik，则[xjk=xik]=0。

步骤4设σ=(σ1,σ2,…,σn)为一个重新排序的随机样本序列，σj表示序列σ中第j个样本，可以将xik替换为

(2)

式中：P表示先验值；a(a>0)表示参数，即先验权重有助于减少低频类别的噪声。

2.2.2 克服梯度偏差

包括CatBoost算法在内的很多Boosting算法都易导致过度拟合问题，可通过建立新树模拟现有模型的梯度，主要包括两个步骤。

步骤1构建树结构。

步骤2确定叶子节点的值。先通过列举各种不同的分割方式构建树，再确定叶子节点的值，随后通过对每种不同分割方式得到的树进行打分，选择最佳的树结构。CatBoost算法通过对经典梯度提升算法的改进尝试解决过度拟合的问题，即先通过无偏估计的方法实现构建树结构，再采取原来GBDT的实施方案确定叶子节点值，叶子节点的值即梯度。

假设Fi是第一次建立i树后构建的模型，由于在模型计算过程中，作为重要因素的梯度值会产生偏移，导致结果可信度及解释力降低。因此，采用Ordered boosting方法解决此问题。对于每个Xk，算法训练训练集中不包含Xk的模型Mk。该模型对于Xk不会使用梯度估计进行更新，但会对其余样本的梯度进行估计。最后，使用这些梯度训练基学习器并得到最终模型。此外，CatBoost训练时会生成s个随机排列的训练数据集，以此加强模型的鲁棒性，并对随机置换进行采样并获得梯度，避免过拟合现象的发生。

2.3 10倍交叉验证

考虑单次划分训练集和测试集易导致计算结果的偶然性。因此，采用10倍交叉验证的方法降低偶然性，提高泛化能力[17]。10倍交叉验证原理如图2所示。

图2 10倍交叉验证原理

2.4 模型评价

对不同算法的预测模型运用混淆矩阵(Confusion Matrix，CM)进行性能评价，其是一个用来总结分类器评价指标的矩阵[15]，常见的二分类问题的混淆矩阵如表4所示。

表4 混淆矩阵

其中：PT表示真正例，真实值为正，预测值也为正；PF表示假正例，真实值为负，但预测值为正；NF表示假反例，真实值为正，但预测值为负；NT表示真反例，真实值为负，预测值也为负。

根据上述4个数值可以得到评价预测模型性能的常用指标，包括准确率、召回率和F1值，具体计算表达式分别为

准确率和召回率是一对矛盾的度量。一般来说，准确率高时，召回率往往偏低；召回率高时，准确率往往偏低。考虑F1值是精确率和召回率的调和值，选用准确率，召回率和F1值3个评价标准。

3 学生就业能力预测实验及分析

3.1 数据采集及预处理

选取某高校2019—2020届电子信息类硕士研究生作为研究对象。依据每个数据库中的共同信息，即“学号”和“姓名”，将多个数据库进行集成，组成一个数据仓库。再从数据仓库中提取相关信息组成数据集，包含有学号、姓名、获得技能证书、学位课成绩、期刊论文发表情况、专利申请获批情况、参与学科竞赛情况、参与科研项目情况、获得创新基金情况、学业奖学金、图书阅读量、毕业论文情况及就业情况等信息，共收集到了961个电子信息类硕士研究生样本数据。其中，就业硕士研究生样本占95.32%，未就业硕士研究生样本占4.68%。

对原始数据集进行数据类型转化、缺失值处理、数据的标准化及数据的过采样。整个数据集进行标准化处理后的部分样本数据如表5所示。

表5 数据集标准化处理后部分样本数据

3.2 模型参数设定

为了训练得到电子信息类硕士研究生的就业能力预测模型，设定了CatBoost算法的参数学习率、树最大深度、过拟合检测阈值以及最大叶子树等10项相关模型参数。具体模型参数如表6所示。

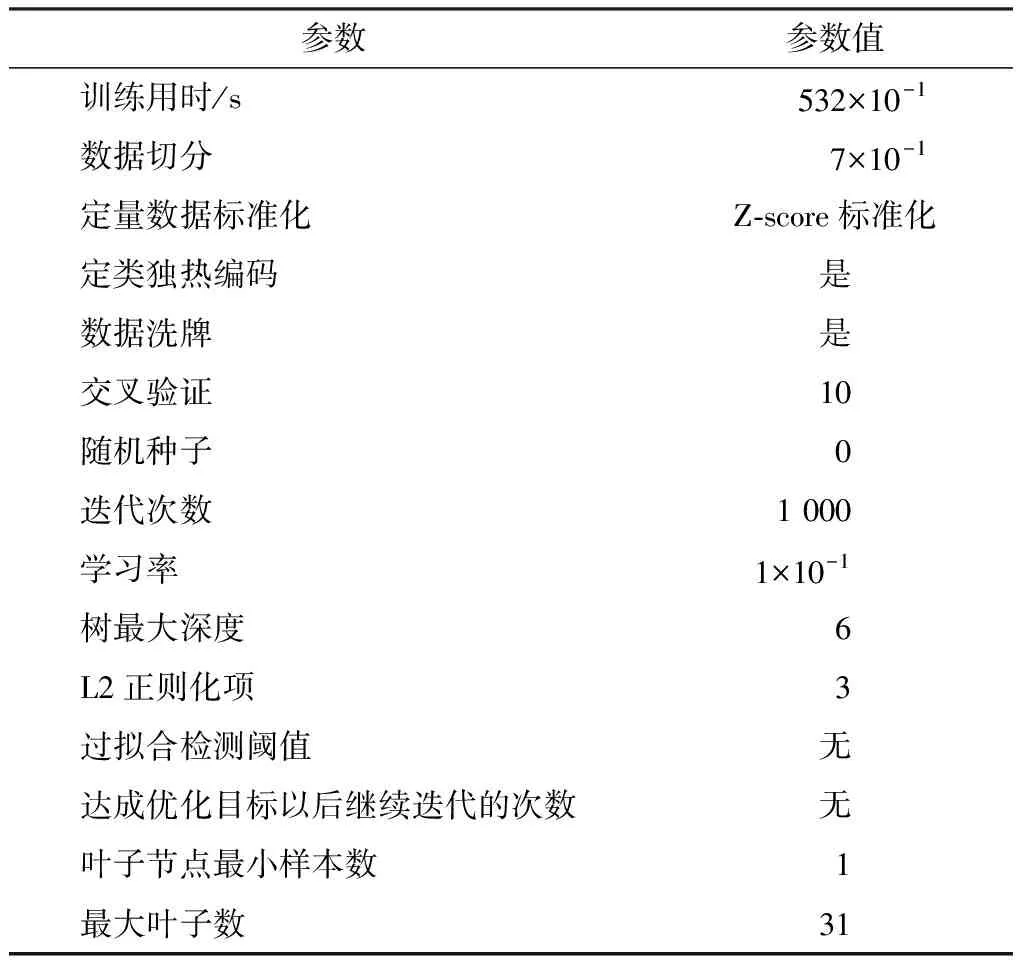
表6 模型参数

3.3 不同算法的就业预测性能对比

在预测硕士研究生就业能力时，采用10倍交叉验证方法提升模型的泛化能力，将原始数据集划分为10个子数据集，轮流将每个子数据集作为验证集，其余作为训练集，共训练10次。

为了验证该模型的预测性能，将CatBoost算法与其他机器学习算法进行对比，按召回率、精确率、F1值及误判率分别进行排名。将所有排名相加得到综合排名作为最终的评价指标。不同算法就业能力预测模型性能综合排名如表7所示。在召回率、精确率、F1值以及误判率4项指标中，CatBoost算法均排名第一。此外，AdaBoost、GBDT、随机森林以及决策树等算法各项指标与CatBoost算法均有一定差距，朴素贝叶斯、支持向量机和逻辑回归则相差较大。CatBoost、AdaBoost、决策树以及GBDT算法均是非线性模型。而朴素贝叶斯、支持向量机和逻辑回归均是线性模型，这表明硕士研究生就业能力相关数据往往呈现复杂的非线性关系。

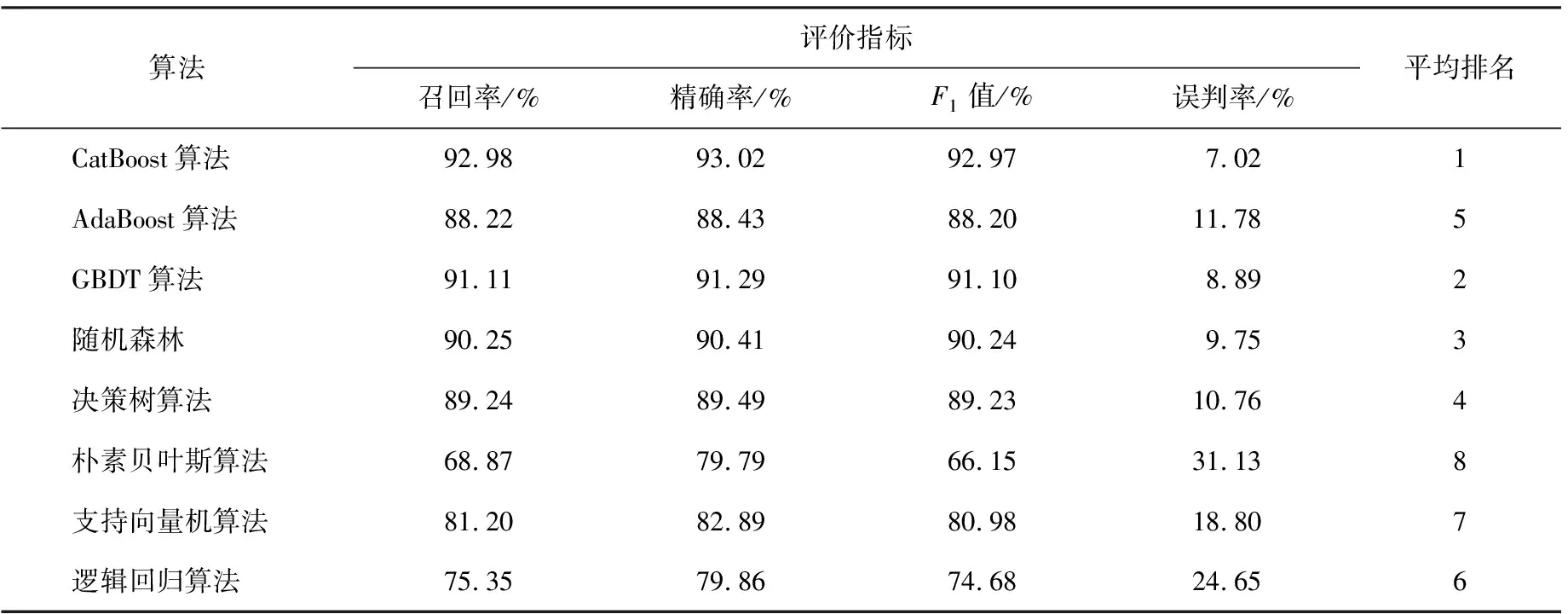
表7 不同算法就业能力预测模型性能对比

3.4 结果分析

经过指标选取与10倍交叉验证与不同算法对比可得，该算法与朴素贝叶斯、支持向量机、逻辑回归等算法在召回率、精确率、F1值和误判率等方面比较而言，预测效果更优。

同时，经过最终的观测指标，在最终环节得到的观测值表中，科研项目、图书阅读量、期刊论文及学位课成绩对就业能力的影响力度比较大，具体如图3所示。

图3 10个观测指标对就业能力影响程度排名

4 结语

为了预测硕士研究生的就业能力，通过Z-core对原始数据进行标准化和SMOTE过采样处理，采用CatBoost算法构建硕士毕业生就业能力预测模型，并与其他算法进行综合对比。研究结果显示，该算法在召回率、精确率、F1值、误判率4项指标方面均优于随机森林、贝叶斯、支持向量机等主流算法。因此，基于该算法的硕士研究生就业能力预测模型的预测能力更强。

基于该研究，将对硕士研究生就业能力的培养从以下两个方面提出建议。

第一，宏观层面。从硕士研究生管理部门角度出发，管理部门在政策支持的同时，可以更加重视在研究生培养过程中对硕士研究生就业能力的培养，设定更多有利于增长硕士研究生能力的项目。如重视奖学金体系，鼓励硕士研究生在校期间发表更多高质量的期刊论文，提高研究能力；着重提升硕士研究生课程质量，在课程设定中加入更多的开放环节，增强硕士研究生的钻研能力；带动硕士研究生有更多机会参与到科研项目中或自己申请科研项目。

第二，微观层面。从硕士研究生个人角度出发，在入学之前，需要对自己所选专业发展前景有清晰的了解，并对未来发展方向有明确的目标设定。在硕士研究生的整个学习期间，在注重学科知识体系的系统化学习的同时，加强科研、外延知识学习、学术论文等能力的培养。