基于改进型协同过滤的网络学习资源推荐算法

王根生，袁红林，黄学坚，闵 潞

1(江西财经大学 国际经贸学院，南昌 330013)

2(江西财经大学 计算机实践教学中心，南昌 330013)

3(江西财经大学 人文学院，南昌 330013)

1 引 言

随着互联网的普及，各种在线网络学习平台迅速发为用展，户提供了丰富的学习资源.面对海量的学习资源如何根据用户的学习兴趣、习惯、能力实现个性化资源推荐是网络学习平台的发展趋势.个性化推荐在电子商业领域运用非常广泛，针对个性化网络学习资源推荐研究方面，国内外学者进行了相关研究探索.陈洁敏[1]对目前学习资源个性化推荐算法进行归纳，总结出主要有基于内容过滤、基于关联规则、基于协同过滤和基于混合模式，梁婷婷[2]通过内容向量空间滤波建立学习资源过滤模型；丁继红[3]在大数据的环境下对学习者、资源、情景等进行多维关联分析，实现资源和学习者之间的个性匹配；沈苗[4]设计一种以学生属性分类为基础的协同过滤算法，实现学生选课系统的智能化、个性化资源推荐；Lei W[5]先通过数据挖掘得到关联规则建立偏好矩阵，再和协同过滤算法混合进行个性化推荐.

基于内容过滤推荐算法需要建立资源特征表示[6]，而网络学习资源形式多样化，很难建立统一的特征表示；关联规则推荐算法需要海量的样本数据支撑，并且个性化程度偏低[7]；资源和用户进行特征表示在协同过滤推荐算法可以省略[8]，通过对资源建立用户兴趣相似度模型，根据兴趣相似用户的偏好对资源进行偏好预测，是目前运用于网络学习资源个性化推荐中最流行的算法.但传统的协同过滤算法面临冷启动和矩阵稀疏问题[9]，针对这两个问题不少学者也提出相关改进方法，管水城[10]提出一种在矩阵分解技术的基础上同时考虑社交网络推荐的新方法，帮助用户在海量的线上异构数据中快速发现其感兴趣的内容；顾寰[11]提出一种融合社区结构和个人兴趣的协同过滤推荐算法，有效缓解了推荐系统数据稀疏性的问题；高玉凯[12]提出一种基于协同矩阵分解的用户冷启动推荐算法，在多个维度上得到用户的潜在特征，缓解冷启动问题；Shulong C[13]在利用用户-项目评价显式信息的基础上，加入其他的隐式信息填充用户-项目评价矩阵，从而缓解评价矩阵稀疏问题；付芬[14]提出一种基于隐式评分和相似度传递的学习资源推荐算法，改进协同过滤推荐算法的相似度计算；丁永刚[15]提出一种改进协同过滤推荐算法，该算发融合学习者社交网络信息，根据社交网络中学习者之间的信任度预测缺失评分，缓解了协同过滤方法的矩阵稀疏问题；Wang X[16]提出一种改进协同过滤推荐算法，该算法的核心是学生在线学习行为序列数据，算法性能相对传统算发得到了改善.通过研究发现，挖掘用户其他潜在特征、添加用户-项目间的隐式信息是目前解决协同过滤冷启动和矩阵稀疏问题的主要思路.

针对网络学习资源推荐这个特定领域，本文引入用户对资源的学习行为日志(分享、收藏、浏览、下载等)缓解评分矩阵稀疏问题，添加用户的学习能力、学习专业、学历、兴趣等潜在特征缓解用户冷启动问题，通过该改进的协同过滤算法来实现更加精准的个性化网络学习资源推荐.

2 传统协同过滤推荐算法

协同过滤推荐算法通常分为两类：一类是基于用户的协同过滤(User-based CF)，另一类基于项目的协同过滤(Item-based CF)[17].User-based CF根据用户对资源的历史兴趣建立用户相似度模型[18]，通过兴趣相似的用户预测评分，把预测评分高的资源推荐给用户[19]；Item-based CF根据用户对资源的历史评价建立资源相似度模型，计算资源间的相似度，然后把和用户历史偏好相近的资源推荐给用户[20].相似度计算是推荐算法的核心部分[21]，主要有余弦相似度、皮尔逊相似度、Jaccard相似度、对数似然相似度[22].余弦相似度是一种比较常用的相似度计算方法，将用户对资源的历史评价表示为向量，用户兴趣的相似度通过评价向量的余弦值来衡量，计算如公式(1)所示.

(1)

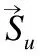
(2)

3 改进型用户协同过滤推荐算法

本文使用基于用户的协同过滤推荐算法建立网络学习资源的个性化推荐系统，针对协同过滤推荐算法的矩阵稀疏和冷启动问题，引入学习行为日志和用户初始化标签进行算法改进，具体算法如下：

算法1.改进型用户协同过滤推荐算法

Step 1.根据用户历史资源评价，生成用户资源评价矩阵；

Step 2.根据用户资源学习行为，生成用户资源行为矩阵；

Step 3.基于用户资源行为矩阵，调整用户资源评价矩阵，生成用户-资源矩阵；

Step 4.根据用户能力、专业、兴趣和学历标签，生成用户初始化标签；

Step 5.根据用户-资源矩阵和用户初始化标签，计算用户相似度；

Step 6.产生推荐结果.

算法1的具体算法模型架构如图1所示.

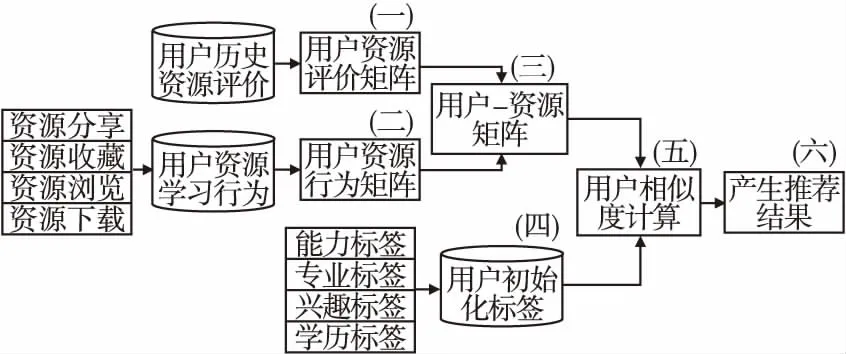
图1 算法1改进型用户协同过滤推荐算法模型架构

3.1 用户资源评价矩阵

将用户对资源的历史评价转换成分值矩阵，形成M×N的矩阵，如图2所示.

图2 用户资源评价矩阵

Uk为第k个用户，ij为第j个资源，rkj为用户k对资源j的评分，取值范围为0-10，没有评价过的资源默认为0，当资源数比较多时，用户评价的资源可能只有很少的一部分，所以整个矩阵中大部分的值为0，导致整个矩阵稀疏.

3.2 用户资源行为矩阵

用户对网络资源的操作不仅仅只是直接的获取与评价，中间也会进行分享、收藏、浏览、下载等学习行为.这些操作行为也侧面反映了用户对资源的学习兴趣，所以通过收集用户学习行为日志，分析其学习行为轨迹，建立行为轨迹与资源评价的关系，从而挖掘用户的相似度，一定程度上可以改善协同过滤算法的矩阵稀疏问题.把用户对资源的相关学习行为转换成对应的兴趣评分，分值通过调查问卷方式获取，问卷给定15种学习行为，被调查者根据自己以往的经验给与不同的评分，例如对某个学习资源只是点击浏览了一下，说明用户对该资源评价可能不高，而用户对资源进行了浏览+收藏+下载+分享，说明用户对该资源评价应该挺高.问卷一共发放了500份给在校学生，有效回收了421份，统计每种行为的平均分，再规约为0.5的倍数，最终得出的分值如表1所示.

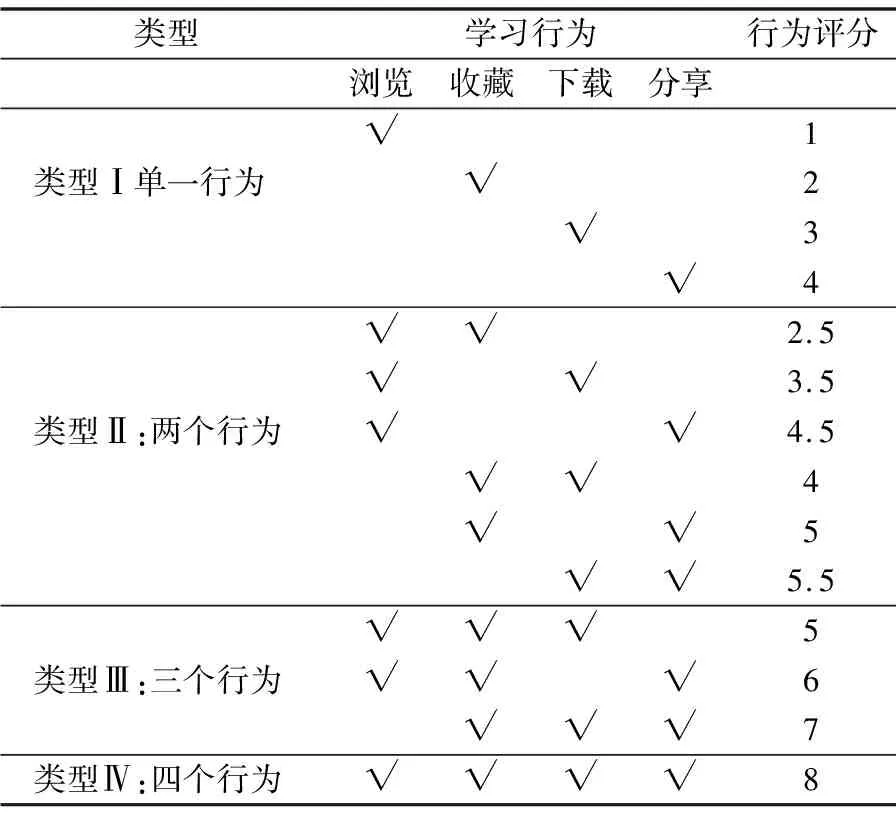
表1 学习行为资源评分

分析用户学习行为日志，构建用户资源行为矩阵，如图3所示.

图3 用户资源行为矩阵

Uk为第k个用户，ij为第j个资源，skj为用户k对资源j的学习行为，取值范围如表1所示.

3.3 用户-资源矩阵

依据用户资源行为矩阵对图2中的用户资源评价矩阵进行调整.如果用户没有对某个资源进行评价过，则分析是否对该资源进行过相关学习行为操作，并根据表1计算相应的分值.经过这一处理，得出用户-资源矩阵，该矩阵的稠密度明显高于用户资源评价矩阵的稠密性.

3.4 用户初始化标签

用户的学习能力、学习专业、学历、兴趣等特征是对用户的直接描述，当一个新用户加入系统时，我们无法根据用户资源评价向量的相似度来查找其兴趣相似的用户，但如果有了这些用户的初始化标签，我们就可以根据这些标记进行用户的相似度计算，从而解决新用户的冷启动问题.用户的标签表示如公式(3)所示.

Tu=[tua,tum,tur,tui]

(3)

tua、tum、tur、tui分别代表用户u的学习能力、专业、学历、兴趣.

1)学习能力：分为4个层次，分别为差、中、良、优，用1-4表示.用户u和v学习能力相似度计算如公式(4)所示.

(4)

2)学习专业：依据教育部的专业分类，共13个学科，92个专业类，630个专业.用户u和v学习专业的相似度计算如公式(5)所示.

(5)

3)学历：分中等和高等教育，中等教育分普通中专、高中，分别用1、2表示；高等教育分专科、本科、硕士研究生、博士研究生，分别用3-6表示.用户u和v学历的相似度计算如公式(6)所示.

(6)

4)兴趣：主要是对那些专业感兴趣，可以多选，但限定不超过5个.用户兴趣的相似度计算如公式(7)所示.

(7)

其中Iu和Iv分别代表用户u和v感兴趣的专业集合，m和n分别代表Iu和Iv两个集合的大小.sim(tua,tvb)的计算见公式(5).

把这四者的相似度进行融合，得到用户初始化标签的整体相似度，计算如公式(8)所示.

simt(u,v)=αsim(tua,tva)+βsim(tum,tvm)+

γsim(tur,tvr)+δsim(tui,tvi)

(8)

在公式(8)中，α+β+γ+δ=1，分别代表对应相似度所占权重，sim(tua,tva)、sim(tum,tvm)、sim(tur,tvr)和sim(tui,tvi)的计算分别为公式(4)-公式(7).

3.5 用户相似度计算

用户相似度采用线性加权方式融合用户资源评分相似度和用户初始化标签相似度，其计算如公式(9)所示.

sim(u,v)=φsimi(u,v)+(1-φ)sim_t(u,v)

(9)

在公式(9)中，φ为融合权重因子，取值范围为[0,1]；sim_i(u,v)为用户资源评分相似度，计算见公式(2)，其用户评价数据来源用户-资源矩阵；sim_t(u,v)为用户初始化标签相似度，计算见公式(8).

3.6 产出推荐结果

得出用户的相似度后，按大小进行排序，选择前k个邻近用户作为目标用户u的相似用户集Su={su1,su2,su3,…,suk}.在相似用户集Su中找出所有目标用户u没有评价过的资源，并预测目标用户u对该资源的评分，具体计算如公式(10)所示.

(10)

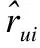
通过公式(10)的计算，给用户u推荐预测评分最高的Top-N个资源.

4 实验分析

4.1 实验数据

实验数据使用JXUFE大学网络教学平台的后台管理数据，平台中包括1215门课程，42452名学生用户，从中随机抽取出3000用户、500门课程作为实验数据.实验数据中包含学生对课程的评分和浏览、收藏、下载、分享等行为记录，以及学生之间的评论和转发记录.由于平台设计之初没有考虑用户的初始化标签，所以后台数据没有关于用户学习能力、学习专业、学历、兴趣的标签记录，但可以通过教务管理系统中的数据，分析出相关的标签值，具体如下：

·学习能力值：根据教务系统中记录的学生考试成绩，得到其学习能力；

·学习专业：根据教务系统数据可以得出其专业；

·学历：根据教务系统数据得到，目前平台只用本科、硕士、博士3种学历；

·兴趣：选择用户评分最高的10门课程所属专业作为其兴趣专业.

4.2 评价指标

实验使用预测评分与实际用户评分的均方根误差(RMSE)进行衡量，RMSE计算如公式(11)所示.

(11)

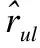
4.3 实验结果与分析

实验步骤如下：

Step 1.根据用户对资源的历史评分得到用户资源评分向量；

Step 2.分析用户对资源的学习行为并转化成资源评分向量；

Step 3.融合Step 1和Step 2的向量，得到最终用户资源评分向量;

Step 4.联合教务管理系统得出用户的学习能力、专业、学历、兴趣标签值；

Step 5.根据公式(2)计算用户资源评分相似度；

Step 6.根据公式(8)计算用户初始化标签相似度，其中α、β、γ、δ，4个权重取值设为1/4；

Step 7.根据公式(9)计算最终用户的相似度；

Step 8.根据Step 7的结果，寻找与目标用户u相似最高的前k个用户；

Step 9.计算目标用户u对资源的预测评分，计算见公式(10)；

Step 10.计算预测评分和实际评分的均方根误差(RMSE).

试验步骤Step 1得到的原始用户资源评分向量的稀疏程度为84%，稀疏程度具体计算如公式(12)所示.

(12)

在公式(12)中，EvalNum表示为用户对课程资源的评价数量，UserNum、ResUum分别为用户总数和课程资源总数.通过Step3融合学习行为资源评分，得到最终的用户资源评分向量的稀疏程度为61%，缓解了矩阵稀疏程度.

4.3.1 不同邻近用户个数k值的实验对比

实验过程中，设定公式(9)中的融合权重因子φ为0.7.邻近用户个数k的取值从10逐步增加到50，每次增加步长为5，共9组实验，分别统计每组实验的RMSE值，实验结果如图4所示.

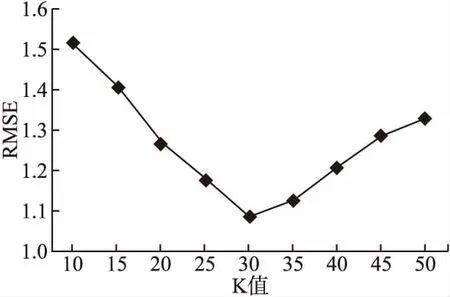
图4 不同k值下RMSE结果

从实验结果可以看出，在该实验设定的参数下，邻近用户个数k为30时RMSE值最小.

4.3.2 不同融合权重因子φ值的实验对比

融合权重因子φ是公式(9)的一个关键因子，它决定了公式(9)中用户资源评分相似度simi(u,v)和用户初始化标签相似度sim_t(u,v)的权重.为了选取合适的φ值，进行了11组试验对比，φ的取值范围是{0,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1}.邻近用户个数k设定为30，实验结果如图5所示.

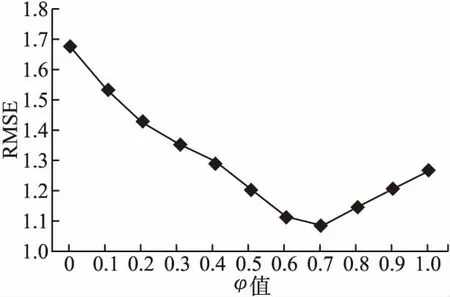
图5 不同φ值下RMSE结果

通过实验发现，在设定参数下，融合权重因子φ为0.7时RMSE值最小.

4.3.3 新用户推荐效果实验

为了验证改进算法对用户冷启动问题的缓解效果，进行新用户的推荐效果验证实验，随机抽取出150个用户作为测试数据.为了模仿新用户，在查找其相似用户时，去除其资源评分相似度，只保留用户初始化标签相似度，实验参数φ取0.7.推荐效果使用平均精准率(precision)和平均召回率(recall)进行衡量，计算如公式(13)和公式(14)所示.

(13)

(14)

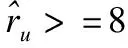
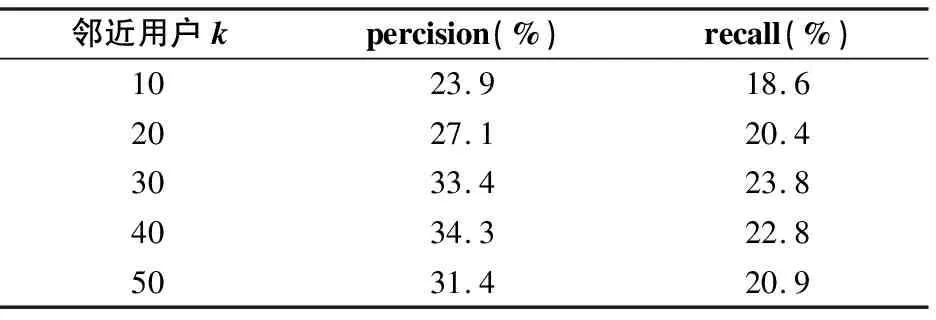
表2 新用户推荐实验结果

通过实验可以看出，本文算法对新用户的推荐也有较好的效果，避免了协同过滤算法因新用户冷启动而无法推荐的问题.

4.3.4 与传统协同过滤算法对比实验

为了验证本文改进算法的性能，将本文提出的算法与另外4类算法进行对比实验，5类算法如表3所示.

表3 5类协同过滤推荐算法

5类算法的最邻近个数都设定为30，IT_UCF的融合权重因子φ设定为0.7，使用RMSE进行衡量，实验结果如图6所示.

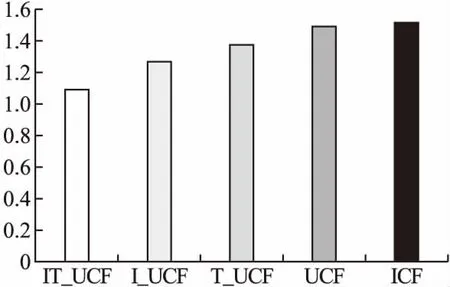
图6 与传统协同过滤算法对比实验结果

通过对比实验发现，I_UCF和T_UCF都比UCF和ICF两种传统协同过滤推荐算法的RMSE值要小，说明引入用户学习行为日志或用户初始化标签相似度确实能改进传统协同过滤推荐算法；IT_UCF算法比I_UCF和T_UCF两种算法的RMSE值要小，说明同时引入用户学习行为日志和用户初始化标签比单独只引入其中一种的效果要好.

4.3.5 与其他改进算法对比实验

为了进一步验证文本改进算法的性能，将本文算法(T_UCF)和基于隐式评分和相似度传递的学习资源推荐算法(CF-IRST)[14]、融合学习者社交网络的协同过滤学习资源推荐算法(Social-CF)[15]和基于在线学习行为序列的学习资源推荐算法(OLSB-UCF)[16]做实验对比.T_UCF融合权重因子φ设定为0.7，CF-IRST的传递路径阈值设定2，Social-CF信任度计算权重参数α设定为0.4，OLSB-UCF聚类k设定为5，邻近用户个数k的取值从10逐步增加到50，每次增加步长为5，共9组实验，把RMSE值作为实验对比结果，结果如图7所示.

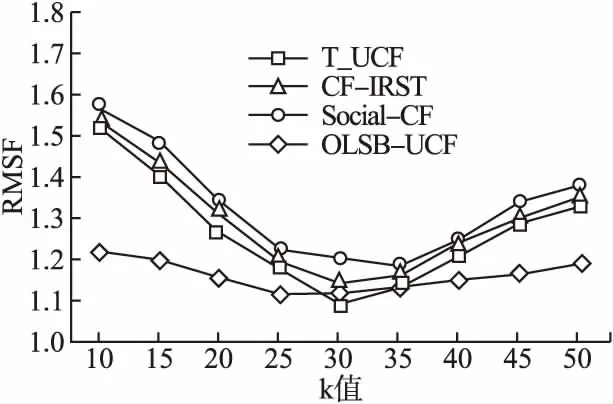
图7 与其他改进算法对比实验结果

通过对比发现，T_UCF，CF-IRST和Social-CF这3种算法随着邻近用户个数k的变化RMSE值具有较大的波动，而OLSB-UCF算法波动较小，这可能是因为OLSB-UCF算法是在聚类的基础上进行的协同过滤，在各自所属的聚类中挑选邻近用户，从而减少了邻近用户个数k的影响.T_UCF相比其他两种改进的算法CF-IRST和Social-CF在不同的邻近用户个数下始终能保持较小的RMSE值，在邻近用户个数k为30左右时RMSE值小于OLSB-UCF算法的最小RMSE值，进一步证明了本文算法的有效性.

5 总 结

智慧网络教育面对海量的在线学习资源使用个性化学习资源推荐是其发展的趋势.针对基于传统协同过滤推荐算法中典型问题—冷启动和矩阵稀疏，提出了引入用户学习行为日志和用户初始化标签的改进型用户协同过滤网络学习资源个性化推荐算法.该算法将用户对资源的操作行为和用户初始化标签添加到用户的相似度计算中.并且通过实验对比证明了该算法的有效性.但本文算法也存在一定不足，一方面是算法存在一定的局限性，在很多其他应用领域用户对资源的操作日志与用户初始化标签不好获取；另一方面，随着时间的推移，用户的学习兴趣、习惯、能力等可能会发生变化，历史数据存在时效性，这种用户兴趣漂移现象本文提出的算法没有考虑.针对这些问题还需进一步研究.