移栽机送苗伺服控制系统动力学建模

崔财豪，曹卫彬

（1.北京吉利学院汽车工程学院，北京102202；2.石河子大学机械电气工程学院）

1 送苗机构方案

取送苗机构是整排式全自动移栽机取送苗的执行机构，其功能是实现钵苗的整排取送。其中送苗机构采用二维双轨同步结构，由同步带模组、联轴器和伺服电机组成，两个同步带直线滑台模组搭建成二维双轨同步结构，由连接轴和联轴器连接在一起，使两个滑台同时移动实现水平方向的精准定位，送苗机构如图1[1]。

实现钵苗水平定位的送苗机构，其执行元件为送苗伺服电机，单个伺服电机通过连接杆将动力传送至“Π”型送苗机构的滑块，使两个滑块同时移动，欲实现整排钵苗的精确取送，必须首先建立送苗机构的数学模型。送苗机构数学模型的建立须考虑交流送苗伺服电机的数学模型、同步带导轨滑块的摩擦之外，还需要考虑送苗伺服电机、连接轴、联轴器、同步带模组的连接方式，本文建立送苗交流伺服电机的数学模型，选择合适的干摩擦摩擦模型解释同步带导轨滑块的摩擦非线性特性，并以此为基础构建移栽机送苗伺服控制系统的动力学模型，为搭建控制系统并对其做进一步深入分析提供理论基础。

图1 送苗机构三维图

2 交流伺服电机数学模型建立

送苗机构工作时由于直线模组和滑台之间的非线性摩擦、结构间隙以及同步带变形等因素的干扰会极大地影响位置精度以及系统动静态性能，因此以研究送苗伺服电机数学解析模型为基础，分析同步带导轨滑块的摩擦特性，建立其伺服运动系统的状态方程[2]。

PMSM（永磁同步交流伺服电机）以三相同步电机作本体，通过三相电枢电流控制输出转矩，具有电流控制简单、转矩波动幅度大等特点[2]。PMSM 伺服系统由控制器、伺服电机、功率变换器、检测元件等几部分组成，如图2。控制器包括位置控制器、电流控制器和速度控制器，分别与由传感器构成的电流环、速度环和位置环相对应；检测元件为电流传感器和速度、位置、磁极位置共用传感器。

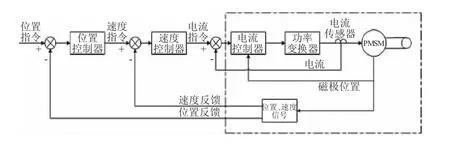
图2 永磁同步交流伺服系统

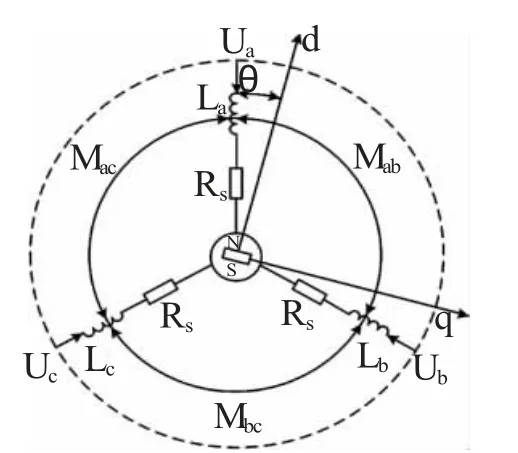
图3 电机解析模型

永磁同步电机精确模型较为复杂，对于一般的控制系统可忽略对控制性能影响不大的次要因素，为便于研究，假设定子三相绕组完全对称、忽略铁心饱和、忽略涡流和磁场损耗、转子上无阻尼绕组、定转子表面光滑[3]。PMSM 中转子磁场的分布和定子绕组的形式决定了电机的特性，以PMSM 闭环伺服控制系统作为研究对象建立数学模型，其解析模型如图3[4]。

三相定子电压方程为：

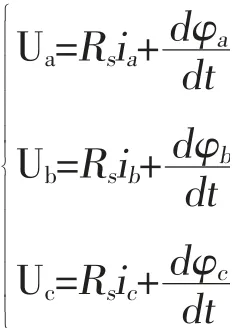
以矩阵形式为：

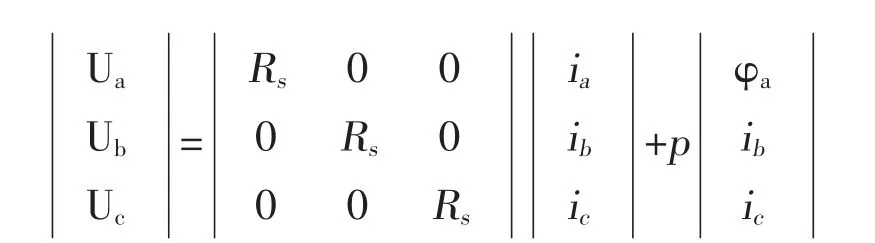
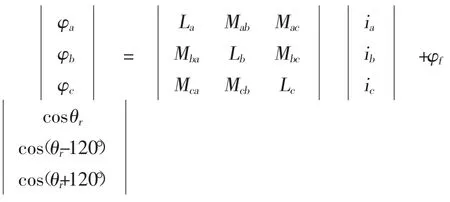
磁链矩阵为：

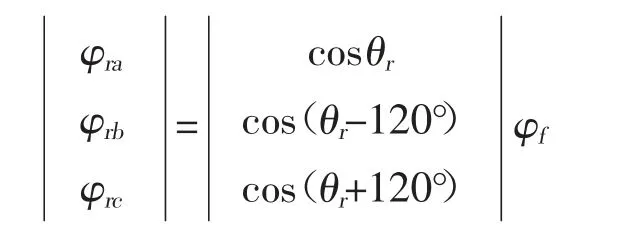
定子磁链方程为：

电磁转矩方程可表示为：

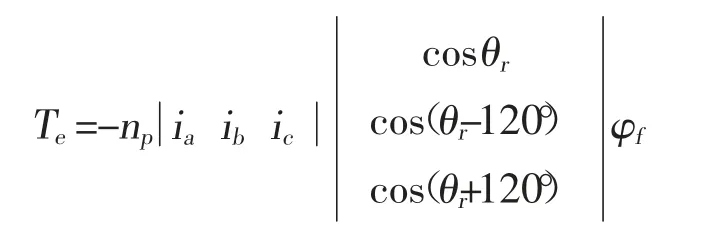
使用Park 变换将三相静止坐标系的电机方程变换到两相旋转坐标系（d-q 坐标系）：

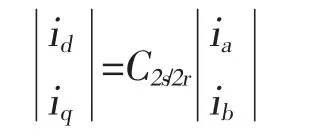
Park 变换矩阵C2s/2r为：

Park 逆变换矩阵C2r/2s为：

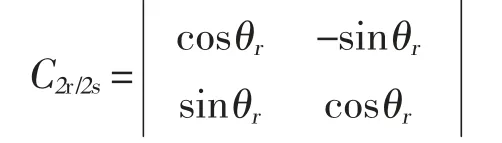
相应电压方程为：

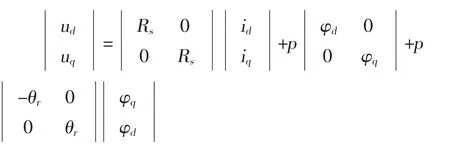
磁链方程为：

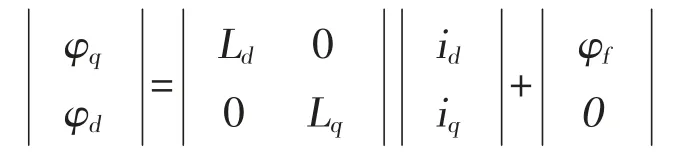
电磁转矩方程为：

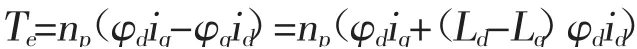
速度指令与输出差值经速度环得到转矩指令值，经电磁转矩公式得到q 轴指令值，设d 轴电流为0，将测到的电机绕组电流经坐标变化得到q 轴实际值，差值经电流环输出电流指令值，并通过坐标变换，经PWM输入至逆变器中，产生定子绕组三相电流，实现PMSM转矩控制[2]。

3 同步带导轨滑块摩擦模型建立

送苗机构工作时，直线模组中同步带与滑块间的摩擦会影响控制系统的精度，为此对同步带滑块之间的摩擦特性进行研究，建立反映同步带导轨滑块摩擦特性的摩擦模型，以克服摩擦对控制系统的影响[2]。Stribeck 模型为机械动力学常用摩擦模型，该模型可以精确地解释导轨滑块间的摩擦特性，不同阶段导轨滑块间的摩擦力与滑块直线速度转化的转子速度之间的关系如下[2,5]：

由于xt=rθm，当时，静摩擦为：

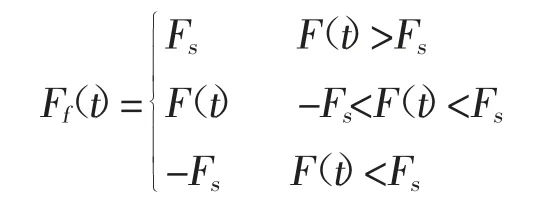
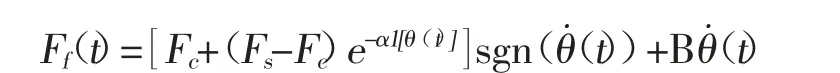
式中F（t）为驱动力矩，Fs为最大静摩擦，Fc为库伦摩擦力，θ˙（t）为转动角速度，α1为经验系数。

4 水平定位伺服运动系统动力学建模

依据送苗机构的组成部分和连接方式，忽略滑块位置变化对刚度的影响，将其简化为如图4 的力学模型。该模型中，联轴器与传动轴被视为刚性联接，并将联轴器与传动轴的弹性变形、联轴器与电机输出轴、传动轴、轴承之间的间隙以及同步带的弹性变形忽略掉，将作用在伺服电机、联轴器、传动轴及轴承间的摩擦等效于作用在电机输出轴上的摩擦。

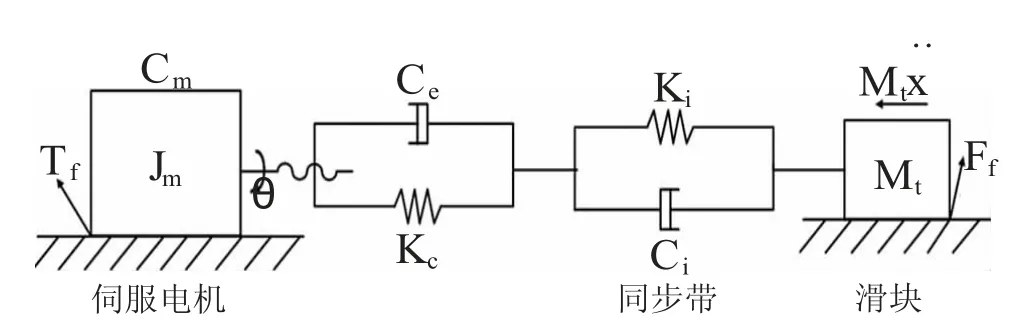
图4 简化力学模型

其中，Kc为等效扭转刚度，Ce为等效阻尼系数，Ki为同步带等效刚度系数，Ci为同步带等效阻尼系数。忽略电动机和联轴器、传动轴的偏差角，将伺服电机和同步带模组的运动等效为一个运动方程：

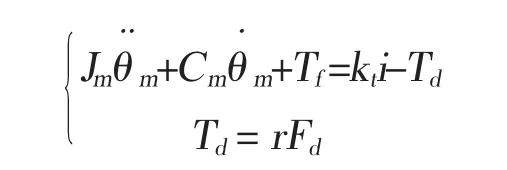
式中i为伺服电机电流指令；Jm为电机旋转部件总转动惯量；Cm为伺服电机总粘性阻尼；Tf为等效库伦摩擦力矩；Td为同步带上的负载转矩；r为直线和旋转运动的转换比，r=L/2π。

将电机转动转化为同步带导轨直线移动：

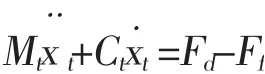
式中Ff为导轨滑块的摩擦力；Mt为导轨滑块的负载质量；Ct为导轨滑块粘性阻尼。

忽略轴间隙以及同步带变形得：

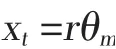
电机处的等效库伦摩擦Tf为：Tf=Tcsgnθm

因此：

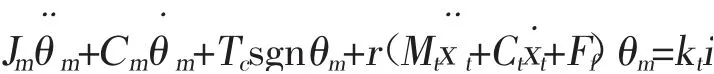
根据上式将其转化为伺服控制系统状态方程：

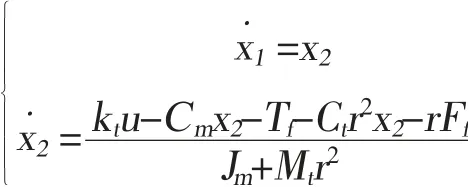
该状态方程可作为送苗伺服控制系统的控制对象模型，输入电流引起被控对象系统状态变化，进而影响输出电机实际转动角度θm的变化。

5 结论

通过对送苗机构的执行元件—交流伺服电机的工作原理和数学模型进行分析，得出经过位置、速度及转矩环输出的q 轴控制电流指令与电机输出转矩的关系，作为送苗伺服控制系统仿真的理论依据。

以整排取苗式移栽机送苗机构的结构及其连接方式为基础构建了送苗机构的简化力学模型，为提高精度，使用Stribeck 模型解释导轨滑块间的非线性摩擦特性，基于简化力学模型建立了送苗机构伺服控制系统的动力学方程，且将其转换为控制系统状态方程，为搭建控制系统并对其做进一步深入分析提供理论基础。