借助数学问题培养小学生数学思维的路径分析

商钦平

摘 要：思起源于疑。有了疑问，才能促使学生积极思考，自觉主动探究。而小学数学作为基础学科，数学学习的本质就是不断思考的过程。所以在教学中要注意课堂提问的艺术性，通过不同问题的设置，激发学生的积极性，拓展学生的思维，提高教学效率。

关键词：小学数学;问题导学;数学思维

亚里士多德说过：“思维自问题、惊讶开始。”问题是激发学生思维的原动力。在数学课堂中，课堂提问是把学生、教师、教材紧密联系起来，它是培养学生学习兴趣、引导学生深入思考、检验学生学习情况的有效途径。有趣的数学问题会锻炼学生的思维能力，培养学生多方位思考能力，课堂气氛活跃，主动参与学习。因此教师应懂得以问导学，以问启智，把问题贯穿于数学教学始终，这是提高数学思维能力的有效途径。

一、 趣味性的问题，营造思考的欲望

托尔斯泰说过：“成功的教学所需要的不是强制，而是激发学生的兴趣。”学习兴趣是产生学习动机的源泉，是促进学生深入主动学习的动力。学生年龄还小，结合教材特点和学生实际情况，一个情境，一个问题，就把学生带进了探索知识的海洋，想去揭开知识神秘的面纱，想去分析、思考、解决，变“要我学”为“我要学”。

比如：在教学“约分”时，笔者出示圆片问：“谁能在1分钟之内涂出这个圆片的75100？”学生个个跃跃欲试，有的学生奋笔疾书，马不停蹄地想完成教师的任务;有的学生冥思苦想，定要找出教师葫芦里卖的啥药;有的学生满脸喜悦，信心十足……通过这样的比赛，学生表示惊奇和困难，呈现出浓厚的兴趣，让学生进一步理解分数的基本性质，感受应用价值和约分的好处，激发学生学习的兴趣。在课堂中，都要学会利用素材和资源，挖掘学生感兴趣的切入点，让学生在轻松快乐的状态下激发思维潜能。

二、 操作性的问题，激发提问的内驱力

小学生以形象思维为主，教师应多提供学生“做”的机会，因为只有自己真正动手操作、实践、观察、思考，才能对知识深层次地理解，以便更好地掌握知识，做到触类旁通。教学中，教师应当尽可能提供增强感性认识的机会，在不断地演示操作中，引发矛盾，提出问题，促进思维。

比如，在教学《植树问题》时，学生猜测：当两端都栽时，棵树比间隔数多1。教师追问：“你怎么知道？”学生建议：“画图解释更直观，一图解千愁呀！”学生发愁了：“100米数据太大了，怎么画？”学生炸开锅了：“可以化繁为简”“选多少米呢”“20米、35米、30米、15米……”学生激烈地讨论，组长有序地安排不同的数据各自验证，得出了共同结论：当两端都栽时，棵树比间隔数多1。是啊，通过动手实践中存在的问题，不断激发他们的提问意识，主动探索问题，自己寻求解决的方案，从而结论水到渠成。

三、 探究性的问题，实现深度思维

直来直去的问题，单调无趣，缺乏启发性，无法拓宽学生的思路，很难调动学生的积极性。而新时代要求学生要有创新性，能够从多种角度思考问题，不单局限于单一模式，这就要求教师在课堂上多设置探究问题，让学生的思维向更深层次拓展，充分培养创新思维的能力。

比如，在初步学习分数比较大小后，出现了这样的一道题（如下）。

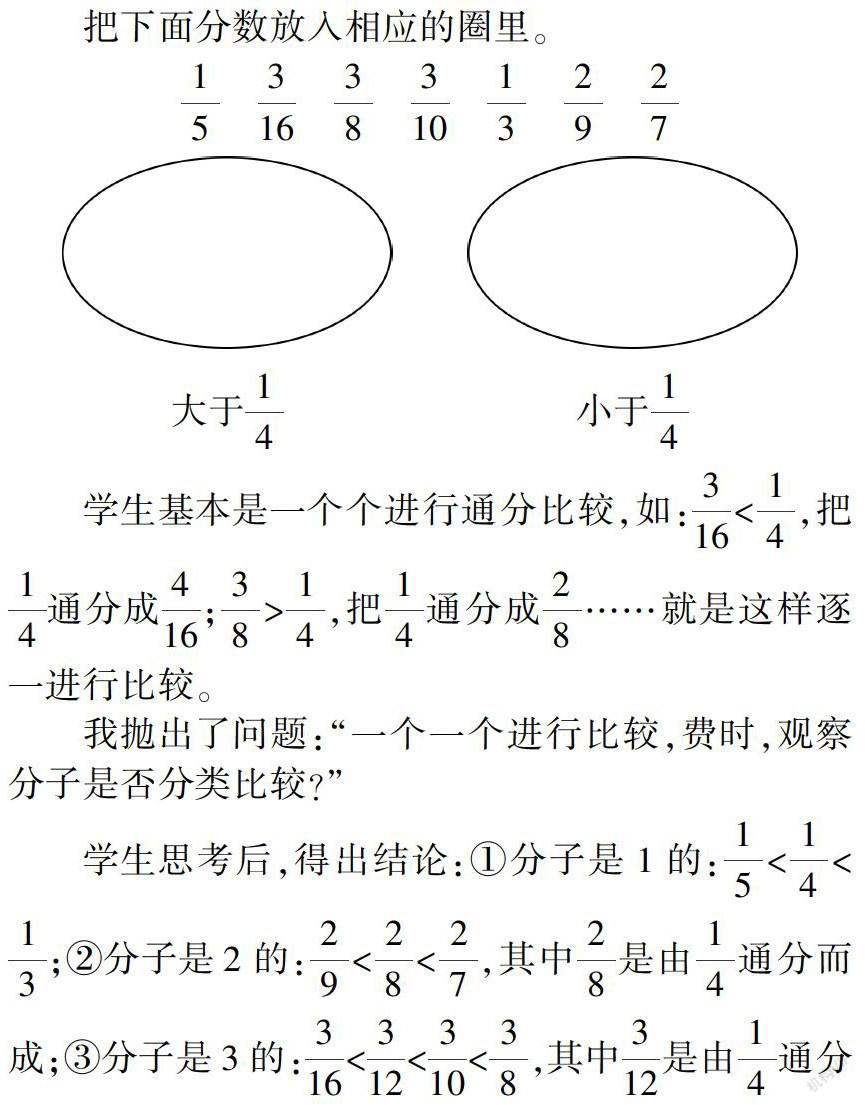
把下面分数放入相应的圈里。

学生基本是一个个进行通分比较，如：316<14，

把14通分成416;

38>14，把14通分成28……就是这样逐一进行比较。

我抛出了问题：“一个一个进行比较，费时，观察分子是否分类比较？”

学生思考后，得出结论：①分子是1的：15<14<13;

②分子是2的：29<28<27，其中28是由14通分而成;

③分子是3的：316<312<310<38，其中312是由14通分而成。一个问题引发思考，分类整理，不仅省时，而且思维清晰、条理性强。

四、 开放性的问题，强化发散的思维

学数学要想办法激活学生的思维，引导他们学会创造性地思考，而开放性的问题不仅可以巩固基础知识，还可以引导学生多角度探究、交流与合作，以便深化和扩展知识。所以在教学中应该有意识地设置开放性问题，关注条件的多种呈现，解决问题步骤方法的多样性和结果开放的程度。让学生从各自身有的认知基础出发，积极参与其中，亲身去体验、建构自己的认知。

比如，在教学《分数大小的比较》综合练习中，按分数的大小从小到大排列：

45，1112，

43，710，12，

56。学生建议：“可以把这些分数全部进行通分，这样就能比较大小了”。问题出来了：“这么多的分母如何找出它们的最小公倍数。”学生开始沉默了，过了十几秒，有学生开始发言：“6和3是12的因数，2和5是10的因数，我们只要找出10和12的最小公倍数就一定是这些分母的最小公倍数。”“有道理，用它们的最小公倍数60通分能解决啦！”正在學生沉浸在成功的喜悦时，笔者又抛出了一个问题：“如果不通分能否解决这题呢？”有学生就开始思考了，接着：“其中43最大，因为它是假分数，其他都是真分数。”“12是最小的，因为其他的数都比一半多。”“剩下的数看看谁跟1最接近，如，45差1个15，1112差1个

112……”就这样用学生的话来说：“不用计算，我竟然看都能看出它们的大小，我们太厉害了！”有的学生开始疑问：能不能把这些分数都化成小数来比较呢？“是啊，小数和分数的互化将是下节课要学习的内容，到时就能用你提议的方法解决了！”问题的开放，且给学生有足够的思考空间，不但牢固地掌握基础知识，还拓宽了思维的深度和广度，得到了许多意想不到的精彩。

五、 生活性的问题，提升应用的能力

现实情境是数学学习进行发展的基础。数学的教学也需要从现实角度来实行。学生在掌握知识的同时，也要学会以变通的思维方式来解决现实问题，感受学有所用。因此，教师在教学中，努力渗透生活思想，创设生活性问题，体验数学知识的价值，激发学生应用能力的发展。