混合驱动无人水下滑翔机耦合运动响应数值预报

凌宏杰，王志东，孙玉山，刘 彦

(1.江苏科技大学 海洋装备研究院，江苏 镇江 212003；2.哈尔滨工程大学 水下机器人技术重点实验室，黑龙江 哈尔滨 150001)

0 引 言

海洋已经成为世界各国战略发展的重要基地，在资源、环境空间和战略方面拥有得天独厚的优势，合理开发、利用、保护海洋是我国21世纪发展的战略需要[1-2]。先进的海洋观测技术、智能化的探测设备是海洋环境探测及资源开发利用的前提，无人水下航行器(Unmanned Underwater Vehicle，UUV)[3]将人工智能、探测识别、信息融合、智能控制、系统集成等多方面技术集中应用于同一水下载体，能够高效率地开展各种探测任务，具有观测范围大、效率高、成本低、机动性能好、续航能力强等优点，在海洋资源开发和观测中发挥越来越重要的作用。

近年来，随着对深远海中长时序、大范围、三维连续海洋环境探测及监测需求的增加，常规UUV受携带能源的限制，在航程与续航能力方面已无法满足需求。为适应长时序、大尺度的海洋探测需求，混合驱动无人水下滑翔机(Hybrid Driven Unmanned Underwater Glider，HUG)应运而生。HUG[4-5]作为一种融合了常规UUV与水下滑翔机(Autonomous Underwater Glider,AUG)优点的新型UUV，可像AUG一样在水中完成具有锯齿形轨迹的滑翔运动且定位精度高，可实现远距离、长时序的要求，也可像水下自航行器(Autonomous Underwater Vehicle，AUV)一样在水中进行推进航行，具有动作反应迅速、跟踪精确的优点及在特定区域内的目标搜索功能。

2001年，由美国Webb公司研发的HUG[6]问世，与美国特利丹仪器公司韦伯海事研究所和伍兹霍尔海洋研究所的斯洛库姆无人水下滑翔机(简称Slocum)相比，该款HUG仅在Slocum的原有尾部构型上增加1个螺旋桨推进器。此后，日本国立海洋研究开发机构和九州大学发明一款新型UUV，该UUV可实现混合驱动[7]，该样机以纺锤形水下滑翔机为基础，在尾部装有螺旋桨推进装置。国内的起步相对较晚：2007年，天津大学开始HUG的研发工作，经过2年多的努力，海燕1号问世[8]；2014年，为使海燕1号满足更多的工程需要，天津大学研究团队[9]进行升级改造，推出海燕2号；2016年，一款HUG科研样机在浙江大学研发成功，该样机创新性地将浮力调节装置设计在首部位置，为实现滑翔与推进混合驱动，在其尾部配备推进器和电动舵。

上述HUG均由回转体和水翼组成，升阻比较小，导致滑翔角较大，在一定程度上影响了水下滑翔机的经济性。此外，上述HUG大多数都在航行器尾部增加推进装置，在遭遇海底洋流和海底旋涡时，运动形式单一，不易快速调整姿态，抗洋流干扰能力较弱。大翼展HUG具有扁平翼型剖面形状的机身，且水翼平滑地与机身融合在一起，具有更高的升阻比[10-11]。此外，大翼展HUG还可在水翼两侧下方各搭载1个推进器，通过对2个推进器进行差速控制，实现更多的姿态和运动控制。

大翼展HUG的大翼展外形使其具有复杂的水动力性能，且与水翼两侧搭载的推进器流场相互耦合，流场特性分析困难；尤其是在水动力性能基础上，添加运动与动力方程，进行耦合运动性能分析，更为困难。国内外对大翼展HUG的耦合运动性能分析研究较少。

本文基于黏性流体理论，采用多计算域、动网格与动力学理论相结合的方法，对大翼展HUG的耦合运动响应进行数值预报与分析，探明其在推进与滑翔模式下的运动响应特性。

1 计算模型

1.1 坐标系定义

HUG刚体可看作由滑翔机本体与左右两个螺旋桨两部分耦合而来，HUG产生的耦合运动是在合力及力矩的共同作用下产生的运动，其中重浮力差、水动力和螺旋桨推力是合力及力矩的主要贡献者。因此，大翼展HUG各个模块间的耦合运动分析显得尤为重要。建立航行器的固定坐标系、运动坐标系和速度坐标系，如图1所示。

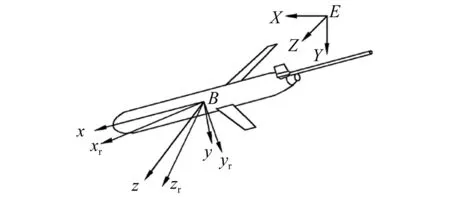
图1 坐标系定义

固定坐标系E-XYZ是以大地为参考建立的。将海平面上HUG的启动点作为固定坐标系原点。根据右手定则定义各坐标轴：取由尾部指向首部的EX方向为X轴的正向；EZ向右侧为正；EY垂直向下为正。

运动坐标系B-xyz的原点B为HUG的浮心。随着HUG的运动，运动坐标系也随之一起运动。运动坐标轴同样符合右手定则：Bx轴沿着HUG的纵向中心线，Bx正向设定为由原点指向艏部；By轴沿着机身的横向，且设定正向为向右舷方向；Bz轴正向设定为垂直机身向下。

速度坐标系B-xryrzr的原点与运动坐标系的原点重合。坐标轴与运动坐标系相似，只是Bxr指向HUG的速度方向。

1.2 计算模型网格划分

基于建模软件完成HUG三维建模，航行器大翼展翼梢下方对称分布导管桨，如图2所示。航行器基础参数如表1所示。导管桨参数如表2所示。

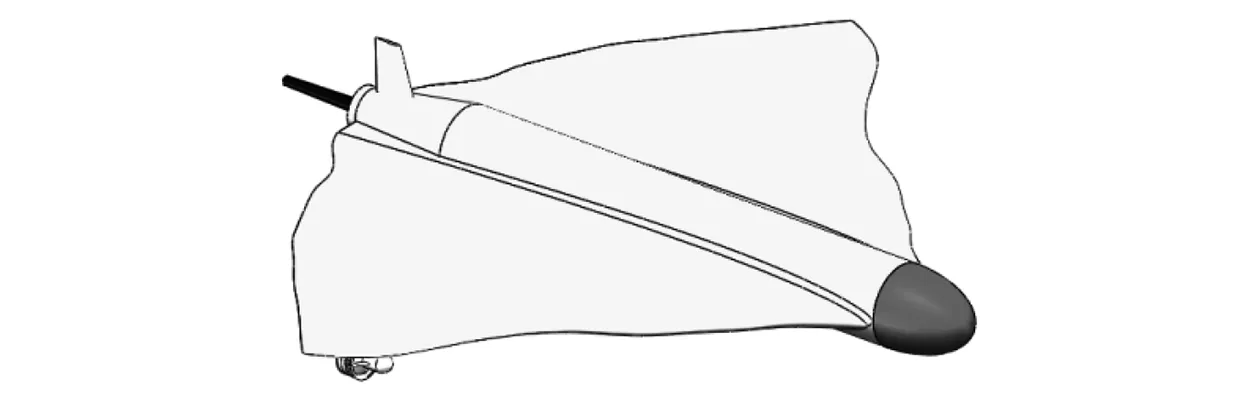
图2 航行器几何模型

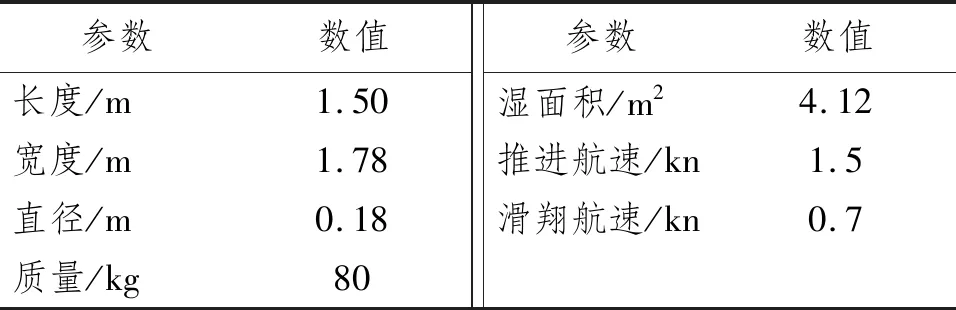
表1 航行器基础参数

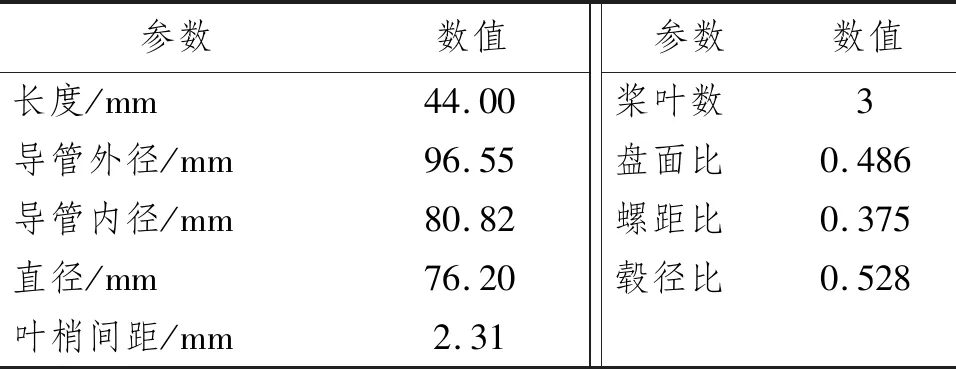
表2 导管桨主要参数

在该计算模型中采用滑移动网格技术将螺旋桨计算域划分为定域与动域，采用八叉树算法生成计算域网格系统。

图3为长方体计算域和航行器表面的网格划分，航行器在长方体域中。航行器特征长度为L，长方体体积为6.0L×4.0L×3.0L，且航行器首部和尾部距入口分别为1.5L和4.5L，距上边界为1.5L、距下边界为2.5L，距左右边界各为2.0L。

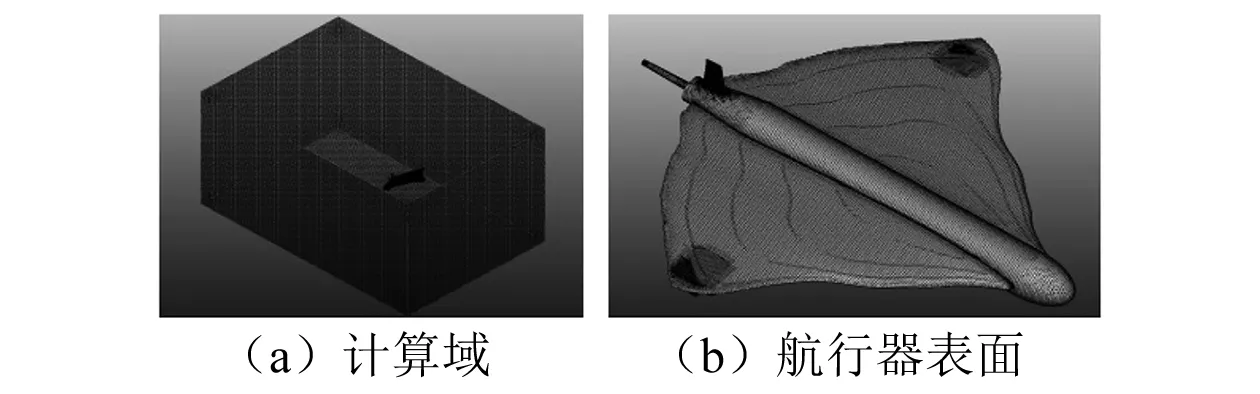
图3 计算域网格划分

图4为旋转域和螺旋桨表面的网格划分，将螺旋桨所处位置划分出螺旋桨旋转域，用于螺旋桨水动力计算。

图4 导管桨旋转域网格划分

在航行器的尾翼和螺旋桨的桨叶顶部局部区域加密处理。计算域网格总数约300万个，其中每个螺旋桨旋转域约50万个。

1.3 计算工况及数值计算方法

1.3.1 计算工况

HUG具有水下滑翔和水下推进两种运动模式，HUG全耦合运动响应数值计算包括4种状态：(1)水平面内的直航运动；(2)水平面内的绕圆运动；(3)水中的下潜运动；(4)水中的上浮运动。

给定螺旋桨转速n为初始条件，完成水平面内的直航运动数值预报，控制螺旋桨转速在600～3 200 r/min均匀取样，转速间隔为600 r/min。给定螺旋桨转速加速时间，时间步长为0.001 s，计算步数为5×104步，所需计算时间为50 s。计算工况如表3所示。

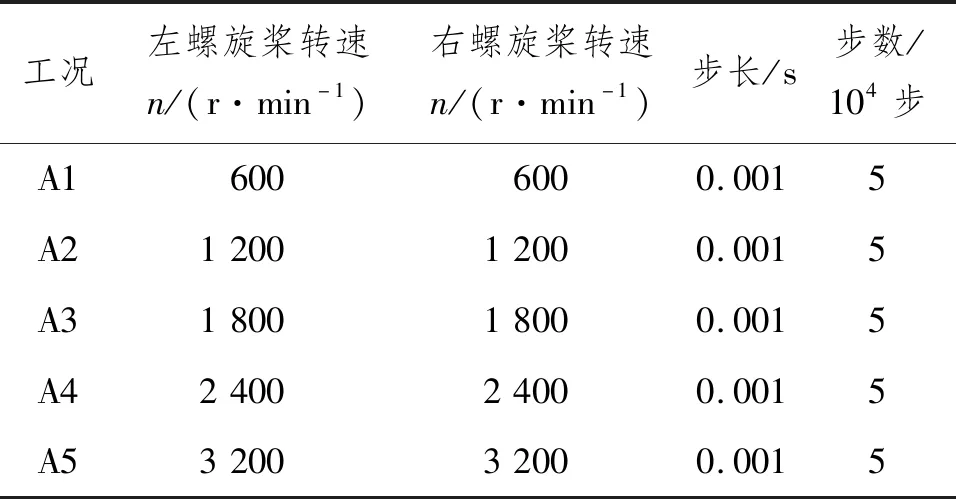
表3 HUG直航运动计算工况

给定左右螺旋桨不同转速(差速推进)，完成HUG在水平面内的绕圆运动数值预报。左螺旋桨恒定转速为1 200 r/min，右螺旋桨转速为1 400～2 400 r/min，时间步长设置为0.001 s，计算步数为4×105步。计算工况如表4所示。

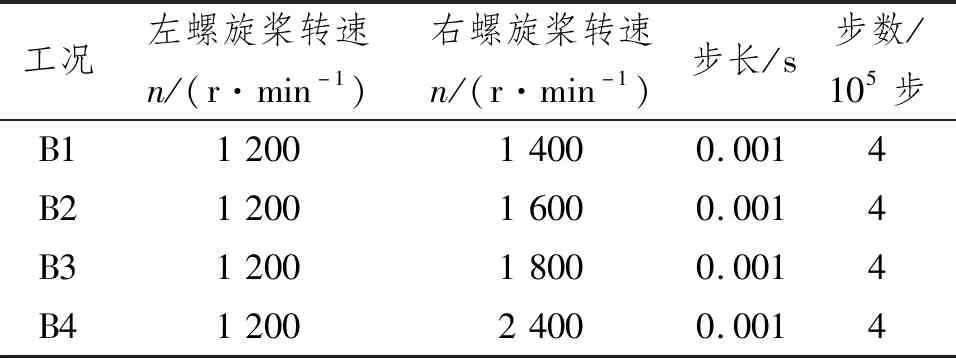
表4 HUG绕圆运动计算工况

对于HUG在水中的上浮与下潜运动数值预报，设重心坐标为(0,0,0)，调整HUG重心与浮心的水平距离，计算稳定时的滑翔姿态角。HUG初始纵倾角β=0°，上浮与下潜浮重力差为分别7 N和-7 N，时间步长为0.002，计算步数为105步。计算工况如表5所示。

表5 HUG上浮、下潜运动计算工况

1.3.2 数值计算方法

计算物理模型选择非稳态模型；选择单相流，流体密度设定为1 026 kg/m3，动力黏性系数取0.001 22 Pa·s；流体模型选择k-omega(SST-Menter)；固壁选择标准壁面函数；选择指定压强条件作为计算域的上下外边界面的边界条件，入口边界、出口边界和两侧边界为远场。在不同运动模式下，HUG在空间六自由度运动方程求解过程中释放的相应自由度如下：

(1) 在推进模式下，采用滑移网格处理螺旋桨旋转域与固定域，整个计算域采用随体动网格，采用铰接方式连接螺旋桨与航行器本体。

① 对于HUG在水平面内的直航运动，释放直航运动方向的单自由度。

② 对于HUG在水平面内的绕圆运动，释放纵荡、横荡和艏摇等3个自由度。

(2) 在滑翔模式下，将螺旋桨与航行器本体固结，对于HUG的下潜和上浮运动数值预报，释放纵荡、垂荡和纵摇等3个自由度。

2 计算结果与分析

2.1 直航运动响应分析

图5和图6为在螺旋桨不同转速下HUG航速时历曲线和HUG阻力时历曲线。由图5和图6可知：在不同螺旋桨转速下，当螺旋桨发出的推力与航行器本体阻力达到平衡时，HUG航速达到稳定值；当螺旋桨与航行器本体在全耦合状态下，HUG航速达0.94 m/s时，阻力为14.1 N，螺旋桨转速约1 800 r/min；当螺旋桨转速为3 200 r/min时，HUG航速可达1.85 m/s。

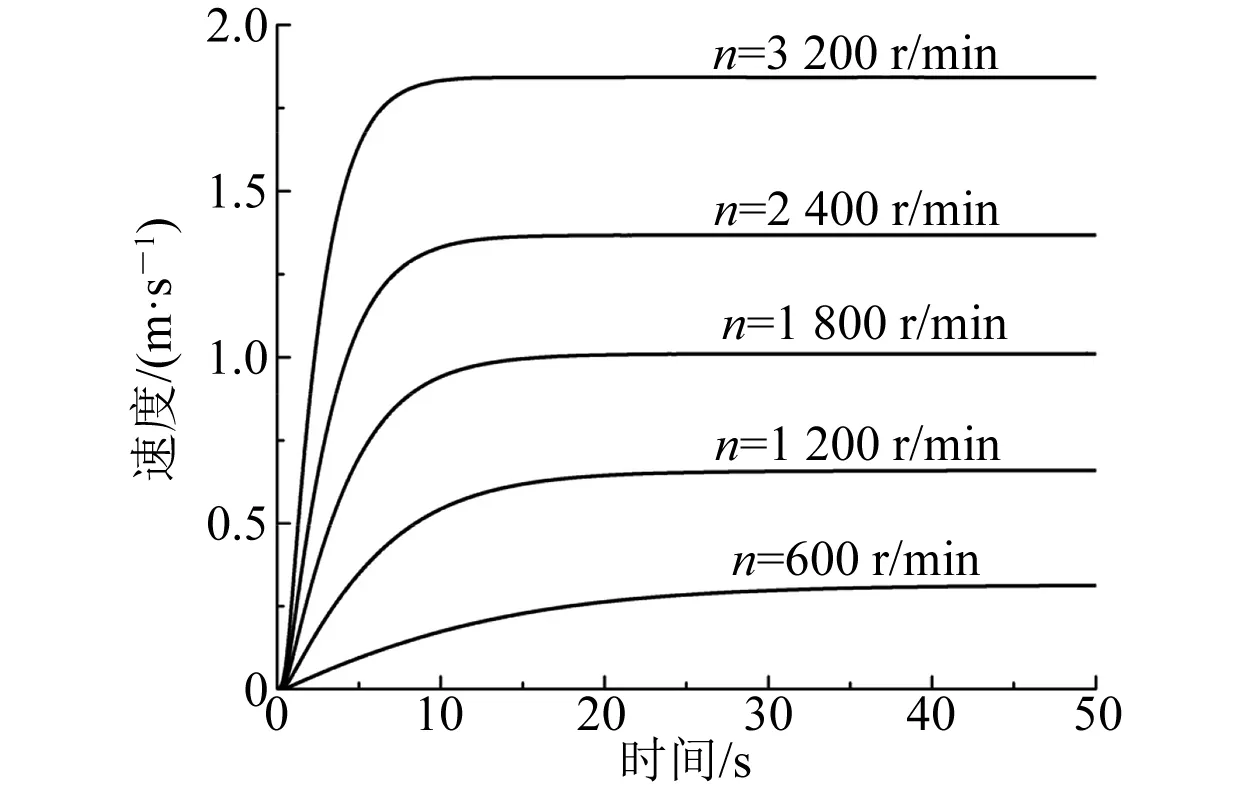
图5 螺旋桨不同转速下HUG速度时历曲线

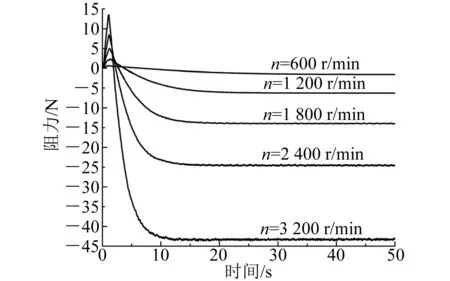
图6 螺旋桨不同转速下HUG阻力时历曲线

2.2 绕圆运动响应分析

图7为HUG绕圆运动轨迹图。由图7可知：在左右螺旋桨不同差速下，HUG进入稳定圆周运动，绕圆运动的直径随着差速增大而减小；在研究工况下最大圆周运动直径为20.50L，最小圆周运动直径为2.04L，表明该款航行器推进器布置方式使其具备较高的机动性能，可通过调整差速达到预期的圆周运动轨迹。

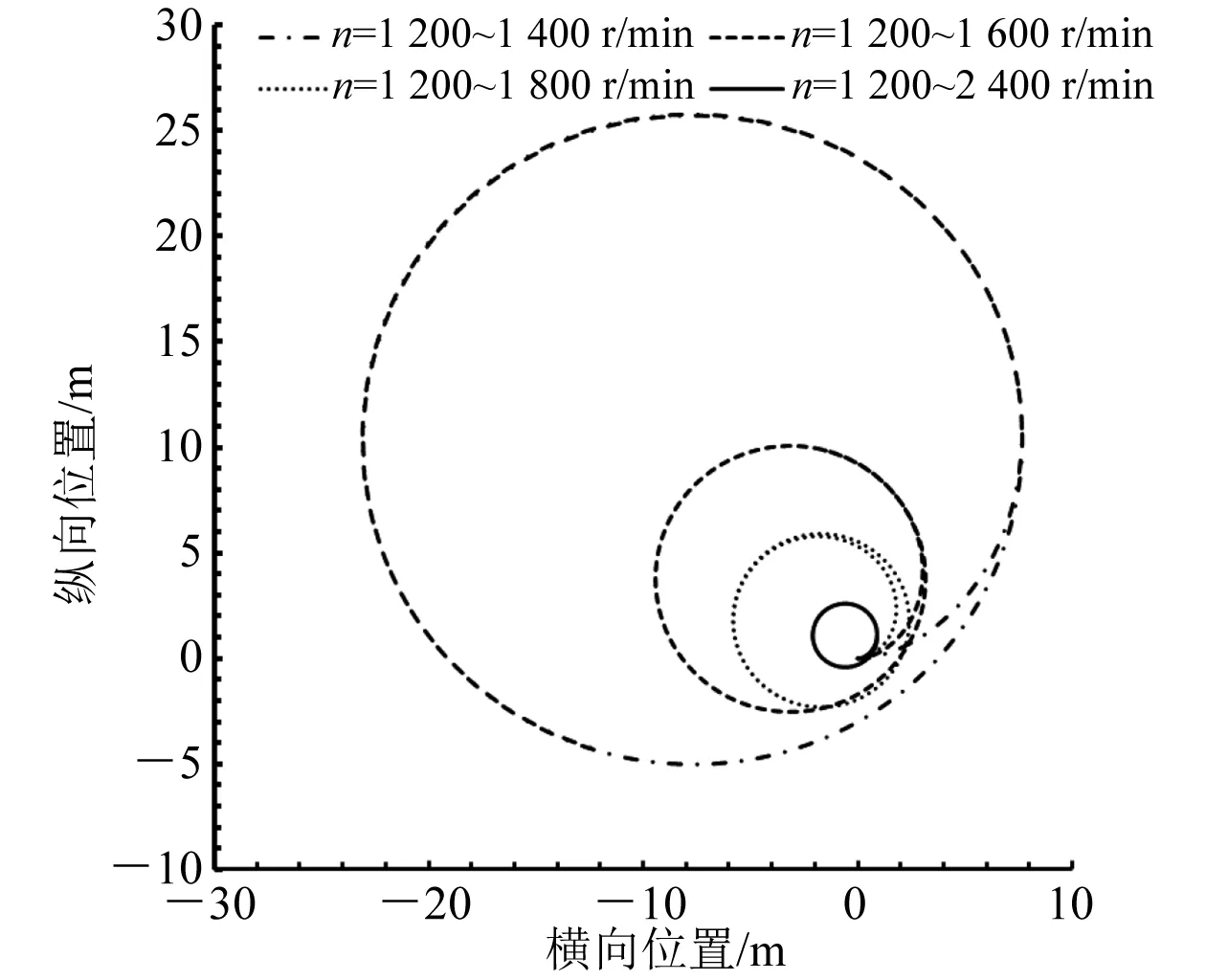
图7 HUG绕圆运动轨迹

图8为航行器回转速度矢量图，不同圆形半径表示HUG运动速度，绕圆运动速度随着差速增大而减小。由图8可知，在左右螺旋桨不同差速下，HUG在x和y方向均可达到稳定航行速度。

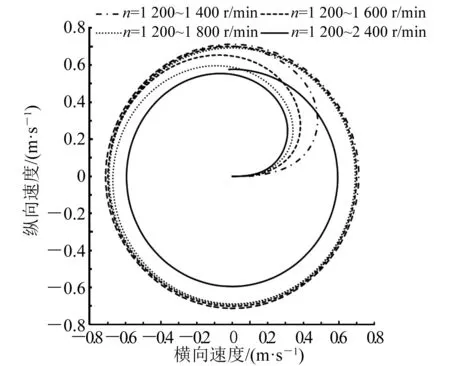
图8 HUG回转速度矢量图

在不同差速下HUG回转直径与回转末速度如表6所示。

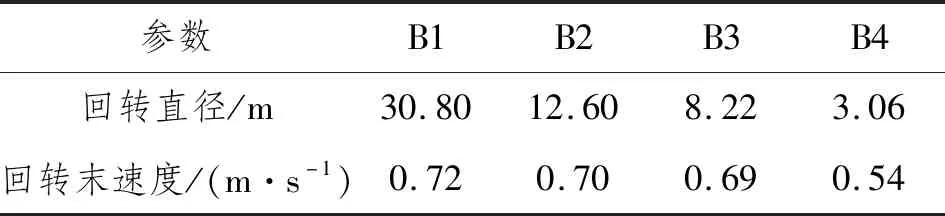
表6 回转半径与回转末速度

2.3 HUG上浮与下潜运动响应分析

图9～图12分别为HUG上浮、下潜运动时x方向和z方向速度时历曲线图与HUG上浮、下潜运动时纵倾角时历曲线图。由图9～图12可知：

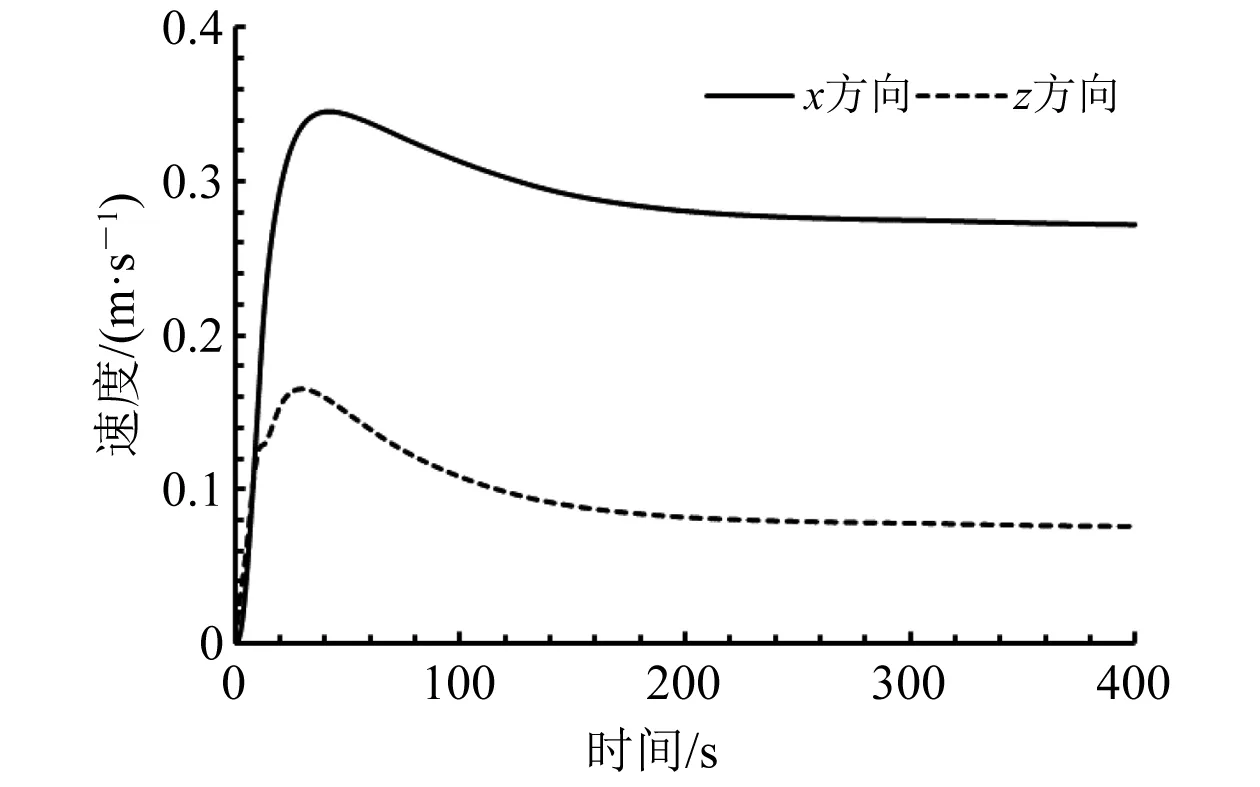
图9 HUG上浮时x和z方向速度时历曲线

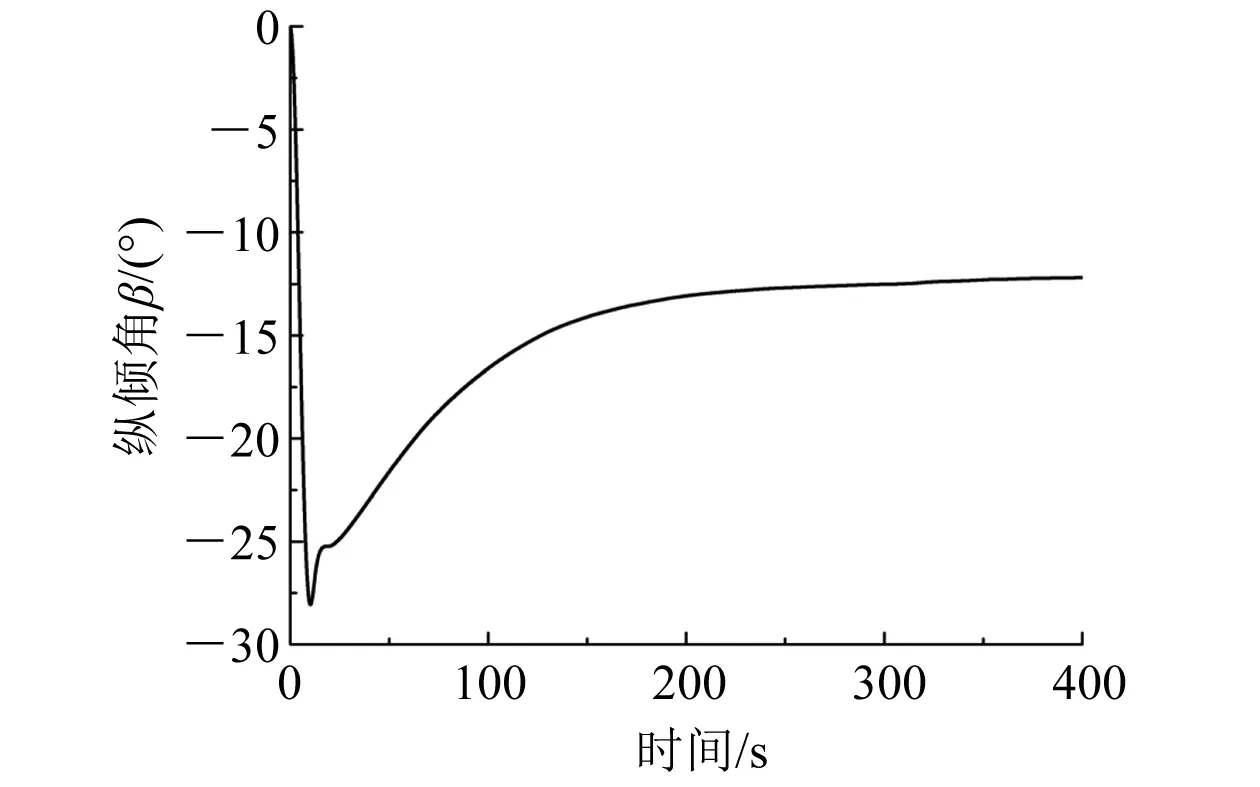
图10 HUG上浮时纵倾角时历曲线

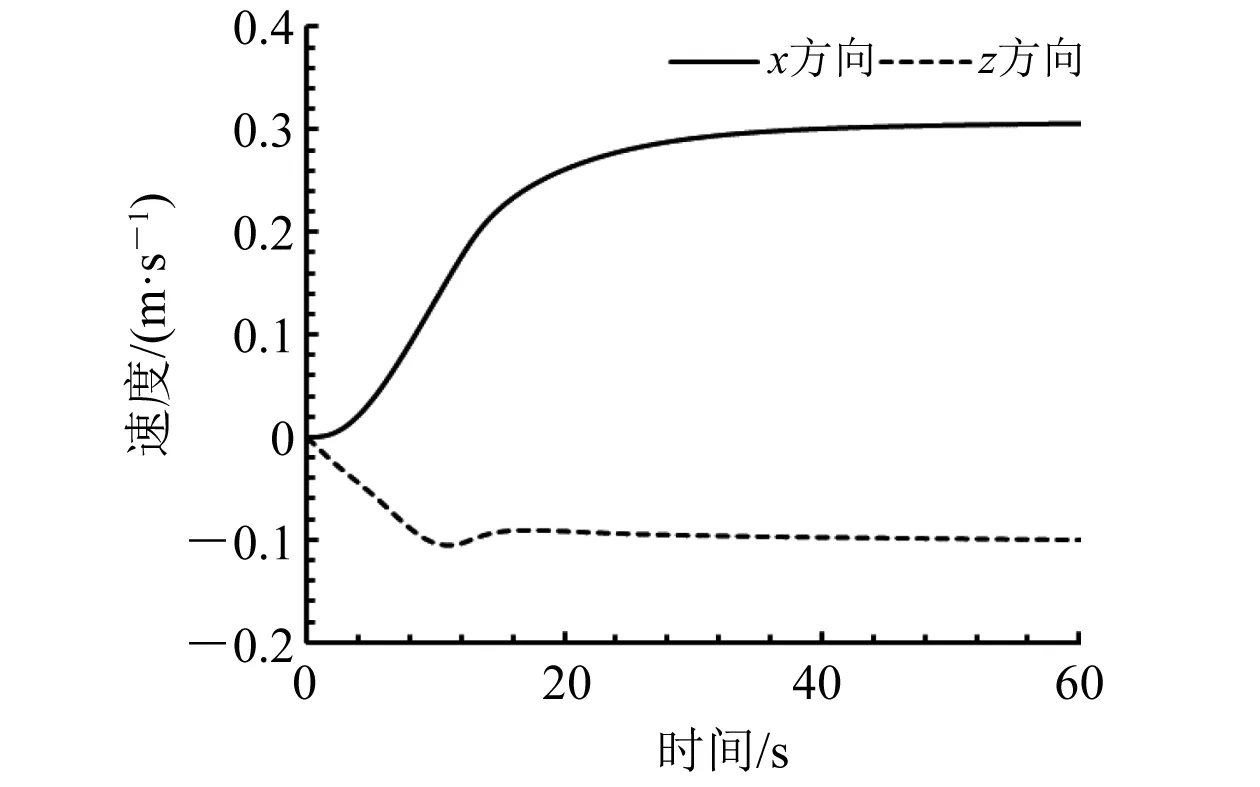
图11 HUG下潜时x和z方向速度时历曲线

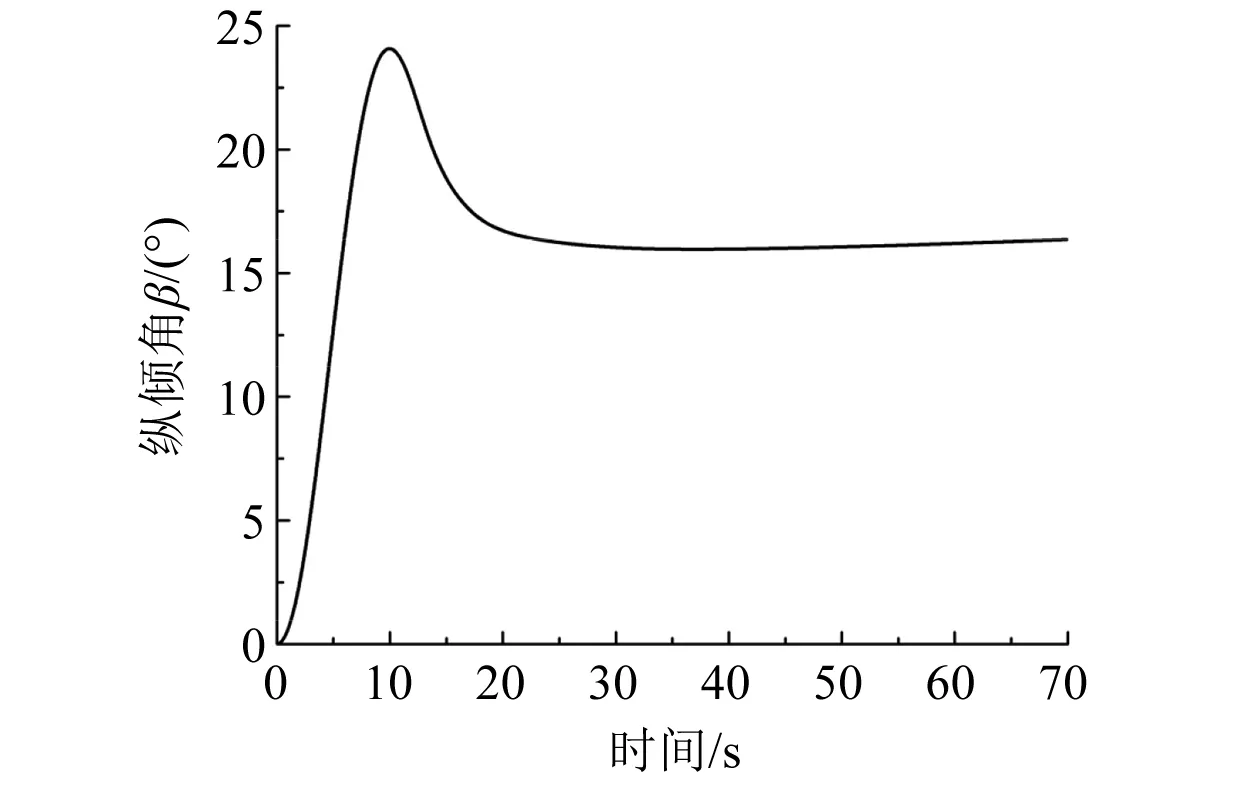
图12 HUG下潜时纵倾角时历曲线

(1) 当HUG上浮时，x方向和z方向达到稳定速度，x方向速度为0.32 m/s，z方向速度为0.10 m/s。

(2) 当HUG下潜时，x方向和z方向达到稳定速度，x方向速度为0.28 m/s，z方向速度为0.07 m/s。

(3) 由于翼展下缘布置的2个推进器引起航行器上下表面不对称，在航行过程中不同迎流攻角产生的水动力阻力不同，在下潜时推进器处于迎流面，产生阻力明显大于上浮时处于背流面状态，因此HUG上浮的稳定航速大于下潜状态。

(4) 当HUG上浮时，纵倾角β=14.3°，下潜滑翔角为17.4°。与海燕2号的下潜滑翔角(27°)相比，该HUG滑翔角更小，在下潜深度相同时，水平方向位移更大，使该HUG工作效率更高，表明大翼展航行器的高升阻比特性在实现水下航行器的长航程方面具有一定的优势。

3 结 论

与由回转体和水翼组成的混合驱动UUV相比，大翼展HUG具有更高的升阻比，且在翼梢下方布置推进器，对两个推进器转速进行控制可实现HUG航行姿态和运动控制。

基于黏性流体理论，采用滑移和随体动网格技术，耦合求解运动方程，开展HUG在推进和滑翔模式下运动响应的数值预报，对航行器的结构和控制系统设计具有重要的指导意义。主要结论如下：

(1) 当左右推进器转速为1 800 r/min，HUG达到设计航速1.5 kn时，HUG总体阻力约15 N。

(2) 在左右螺旋桨不同差速下HUG均进入稳定圆周运动，绕圆运动直径随着差速增大而减小，在计算工况中最大回转直径为20.5L，最大回转速度为0.72 m/s。

(3) 翼展下缘布置2个推进器，引起航行器上下表面不对称，因此在下潜时推进器处于迎流面，产生阻力明显大于上浮时处于背流面状态，HUG上浮时的稳定航速大于下潜状态。

(4) 采用大翼展构型，HUG上浮和下潜滑翔时的纵倾角分别为14.3°和17.4°，优于同类航行器的纵倾角(27°)，表明大翼展航行器的高升阻比特性在实现水下航行器的长航程具有一定优势。