降雨对花岗岩风化层路堑边坡滑动模式影响——以福建云平高速云霄段为例

蔡荣坤，戴自航，徐根连，胡长江

（1.福州大学土木工程学院，福建 福州 350116；2.福建省建研工程检测有限公司，福建 福州350007；3.福建第一公路工程集团有限公司，福建 泉州 362000）

0 引言

设计的道路（包括公路和铁路）途经山地或丘陵时常常存在不少放坡开挖地段，由此形成路堑边坡。从经济角度考虑，许多路堑边坡设计上常是根据工程勘察报告提供的沿线岩土层分布及其物理力学参数再参照相关国家规范或经稳定性分析后按一定坡率进行无支护放坡（有的仅做护面处理，如拱形骨架植草或灌木+表面截排水处理等）。虽然这样的边坡理论上应该是稳定的，然而现实情况是各地仍有大量这类边坡出现浅层滑坡、滑塌或溜滑，且这样的情况大多发生在短时强降雨或长时间连续降雨之后。土质路堑边坡在一般工况下，常具有较好的稳定性，但在降雨入渗作用下，由于随土体含水量增加其自重增加且土中基质吸力降低，致使边坡的稳定性将出现不同程度的下降，并且可能使潜在最危险滑动面位置发生变化，从而出现上述灾害。

自1975年ZIENKIEWICZ 提出强度折减法[1]以来，随着计算机和数值计算技术的发展，国内外学者运用强度折减法在临界失稳的判据、安全系数的影响因素、降雨入渗对安全系数的影响等方面进行了较为广泛和深入的研究[2-4]。如张昊等[5]通过在快速拉格朗日有限差分程序FLAC3D中采用强度折减法分析了边坡滑动面与内摩擦角和黏聚力的对应关系，结果表明，滑动面位置受内摩擦角和黏聚力的共同影响，且随着黏聚力的增大，滑动面趋于平缓，滑体体积逐渐增加；刘明维等[6]采用有限元强度折减法，通过人为依次约束复杂滑坡算例的潜在剪出口，设定不同的治理方案计算得出所有潜在的次级滑动面，可为工程治理提供借鉴；毕港等[7]利用FLAC3D自带的强度折减法计算边坡最小安全系数及滑动面，通过手动折减强度参数，并适度放大分析步数，如此反复求得潜在的次级滑动面，且与Bishop 法进行对比，结果表明该法准确性较高，在方案设计中有必要考虑不同情况下的滑动面形式；李小春等[8]提出用局部折减法进行边坡多滑动面计算，即首先计算初始状态下各单元的安全系数，后建立不同范围的各单元集合，并对不同单元集合进行强度折减求解出相应的安全系数和与之对应的滑动面。LIN 等[9]认为滑动面以下土体不会发生坍塌，后将滑动面以下土体设为弹性材料，并通过调整弹性材料的高度，以此来获得不同安全系数对应的不同滑动面。但目前，对于路堑边坡在不同工况下潜在最危险滑动面或者说滑动模式可能发生变化的研究相对较少，尤其是在降雨工况下的研究。为此，本文将从实际工程案例出发，着重研究降雨强度、降雨历时及边坡坡率对路堑边坡潜在滑动模式的影响。

1 降雨入渗工况边坡稳定性分析方法

1.1 土的渗透系数和土-水特征曲线

天然状态下，绝大多数边坡内位于地下水位或毛细饱和区以上的土体常处于非饱和状态，但在降雨入渗等影响下，边坡非饱和区土体可能逐渐过渡至饱和状态。一般认为，饱和土的渗透系数为常数，而非饱和土的渗透系数与基质吸力或体积含水量有关，人们曾提出了一系列经验或半经验关系式[10]，本文分析将借鉴ALONSO等提出如下形式[11-12]：

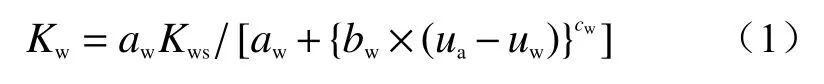
式中：Kw——渗透系数；

aw、bw和cw——参数；

Kws——土体饱和时的渗透系数；

ua和uw——非饱和土中孔隙气压力和孔隙水压力，且ua-uw为基质吸力。

非饱和土的土-水特征曲线亦采用他们定义的饱和度与基质吸力的关系[11-12]：

式中：Sr——饱和度；

Si——残余饱和度；

Sn——最大饱和度；

as、bs和cs——参数。

1.2 土体抗剪强度及强度折减法

土坡失稳主要是滑动面上土体发生整体剪切破坏的结果。目前，广为接受的非饱和土抗剪强度公式是由FREDLUND 等[10]提出的如下形式

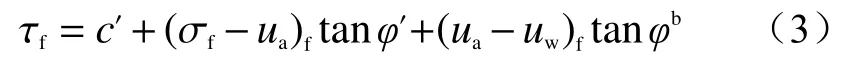
式中：c′——有效黏聚力；

φ′——有效内摩擦角；

(σf-ua)f——破坏时在破坏面上的净法向应力；

(ua-uw)f——破坏时在破坏面上的基质吸力；

φb——抗剪强度随基质吸力增加的速率。

当受降雨入渗等条件影响，非饱和土趋向饱和时，孔隙水压力接近孔隙气压力，即ua=uw，因而式(3)中基质吸力(ua－uw)f=0，净法向应力成为法向有效应力(σf－ua)f=(σf－uw)f=σ′f。即由非饱和土的抗剪强度公式式(3)可平顺的过渡至适用于饱和土的经典的Mohr-Coulomb（简称M-C）抗剪强度公式

由此可见，非饱土向饱和土过渡时，其抗剪强度将降低，这也是自然界中滑坡大多发生在雨季的主要原因之一。

原则上，无论是饱和土边坡还是非饱和土边坡的稳定性分析均可采用强度折减法[13-14]。下文将采用ABAQUS有限元软件，先对路堑边坡自然状态下进行强度折减计算，分析其稳定安全系数和对应的滑动面，后在降雨的工况下设定不同降雨强度和降雨历时计算滑动面的变化情况，并调整边坡坡率探究其对于边坡滑动面的影响。

2 实例分析

2.1 工程背景

福建省在建云平（云霄至平和）高速云霄县境内的浯田互通穿越低山丘陵段。按照我国《JTG D30——2015公路路基设计规范》中对于路堑边坡的规定，高速公路路堑边坡在天然状态工况下安全系数大于1.20～1.30[15]时，可认为其达到稳定状态，当路堑边坡在暴雨或连续降雨的工况下安全系数需大于1.10～1.20 才可认为其处于稳定状态。根据该处线路工程勘察资料和上述规范要求，某段路路堑边坡设计如图1所示，采用两级放坡开挖，无支护，仅做表面植草护坡及拱形骨架截排水处理。该处边坡土层共分为两层，层面不水平，上层土体为全风化花岗岩，呈灰黄色，矿物已完全风化，原岩结构残余可辩，岩芯呈粉土状，无砂感，遇水软化，易崩解；下层土体为砂土状强风化花岗岩，呈灰白色，大部分矿物已风化完全，原岩结构可辩，含未分解的石英颗粒，砂感强，遇水软化，易崩解。

图1 边坡设计断面Fig.1 Design profile of slope

该边坡按原设计要求施工完成后不久，在2018年8月份连续几天中等强度降雨后在AK1+590～AK1+620 段边坡坡脚至一级边坡坡顶（二级边坡放坡平台或称马道）出现了浅层滑坡，如图2所示。事故发生后，笔者采用具有应力和渗流耦合且非线性分析功能优越的ABAQUS 有限元软件，土体材料采用Mohr-Coulomb 理想弹塑性模型模拟，按强度折减法对该路堑边坡开展了各种不同工况下的稳定性分析研究，揭示了其在降雨条件下发生局部浅层滑坡的必然性。

图2 浅层滑坡情形Fig.2 View of a shallow landslide

2.2 一般工况滑动模式分析

根据该处线路工程勘察报告，土层物理力学参数如下表1所示，由于E、υ 无试验数据，且已有研究表明[2-3]，它们的取值在求解边坡安全系数时影响不大，故二者表中取值均为经验值。

表1 土工参数Table 1 Geotechnical properties of soils

为便于有限元模型的网格划分，将图1所示土层分界面按多段折线简化。模型左边界以公路另一侧为界（距坡脚38 m），坡高如设计断面图1标注所示，底部沿路面向下取32 m，整个模型底边长为108 m，有限元几何模型如图3所示。为提高计算机的运算效率并满足计算精度需求（图4），自边坡表面附近往远处采用疏密网格划分方式，即设置斜坡表面及靠近斜坡处单元边长约为0.5 m，模型左、右及下边界处约为3 m，中间部分由1 m 过渡到2 m，采用CPE6 单元。

图3 有限元几何模型Fig.3 Geometric model of finite element

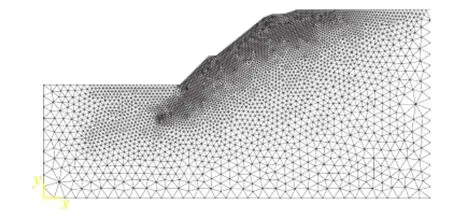
图4 有限元网格划分Fig.4 Finite element meshes

强度折减法的实现是通过ABAQUS 中自带的温度功能对土的抗剪强度指标自动折减进行有限元分析。具体做法是，在材料属性中激活温度变量，并将土的强度指标输入材料属性中，程序便会根据温度变量数值对强度指标进行自动折减分析，此时，即将温度变量数值视为强度折减系数，而非以往常用的场变量数值。值得注意的是，为实现该功能，还需在预定义场中对模型根据分析步指定相应温度数值。为便于在后处理中能直观地观察安全系数的变化情况，可在分析步中的场输出中选择节点温度输出。此方法相较于通过场变量实现强度折减而言，省去关键字编辑语言的繁琐，且根据实际计算分析发现，在后续降雨工况分析中也具有很好的适应性。

一般工况稳定分析不考虑应力与渗流耦合，采用总应力有限元分析方法，即土体抗剪强度指标取表1中的c、φ值。以塑性区从下至上刚好贯通作为边坡失稳判据，分析得到该边坡稳定安全系数为1.200，满足规范要求，滑动面为塑性应变云图的脊线（图5），呈近似圆弧形滑动面。

图5 一般工况塑性应变等值云图Fig.5 Plastic strain contours under general working condition

由水平位移云图6和程序边坡变形动态显示结果可见，边坡变形较大区域主要集中于坡脚偏上位置，即下层土体在坡脚处最先屈服，从坡脚附近滑出，使坡内中部土体失去支承而跟着向下滑移，进而牵引上部土体产生蠕滑，最终导致边坡出现整体失稳。但沿图5所示滑动面产生整体滑动模式与图2的实际情况不符，需作进一步分析。

图6 一般工况水平位移等值云图Fig.6 Horizontal displacement contours under general working condition

2.3 地下水渗流工况滑动模式分析

由前文图1可见，该边坡坡体下部存在地下水，实际开挖时，靠近坡脚边坡表面有地下水出露，客观上可认为当前地下水位以下为饱和土，以上为非饱和土，严格说其稳定分析宜考虑边坡土体的饱和状态，分别采用式(3)和(4)确定非饱和和饱和土的抗剪强度。然而，按式(3)进行非饱和土边坡的稳定分析，需进行非饱和土三轴实验和现场边坡非饱和区基质吸力量测，无论是室内实验还是现场吸力量测都需要价格昂贵的专用仪器和设备及较高的量测技术，且基质吸力大小常随边坡土体中不同位置无规律变化[10]，在数值计算中较难准确考虑，故下文强度折减数值分析将考虑土中渗流和孔隙水压力的影响，但土的剪切破坏仍采用式(4)经典的M-C 准则，即不考虑式(3)右边第三顶即基质吸力对土的抗剪强度的贡献，且从该式可见，因在非饱和区uw为负，因而破坏面上的法向有效应力大于其总应力，即σ′f＝(σf－uw)f＞σf，因而在一定程序上考虑了土的非饱状态对边坡稳定性的有利作用。

本分析网格划分方法同上节，网格单元类型采用的是孔压/位移耦合的CPE6MP 单元。模型底部边界为不排水边界且施加竖直向和水平向约束，其它各面均为透水边界，左右边界按线性孔压设置，即施加水头荷载，根据现场勘察资料可将左边界零水头设为与路面标高一致，并施加水平向约束，且在路面施加孔隙压力为0 的边界条件，右边界水头高度设为距离模型底部38 m（即路面标高以上6 m）。采用有效应力有限元分析法，土的抗剪强度指标采用如表1中的c′、φ′值。研究表明[16]，不同各向同性渗透系数土体对边坡稳定性影响可忽略不计，因而，此处按经验取上、下两层土体饱和渗透系数分别为Kws＝3×10-4m/s 和5×10-5m/s，且在无试验资料基础上参照文献[12]中花岗岩残积土，取式(1)中参数aw＝1 000、bw＝0.01、cw＝1.7 分别取为1 000、0.01，取 式(2)中 参 数Si＝0.08、Sn＝1、as＝1、bs＝5×10-5、cs＝3.5。从而可得到图7所示边坡孔隙水压力分布等值云，可见，稳定渗流状态下孔压为零的地下水位线与图1现场勘察所得基本一致，该线以下孔压为正，以上孔压为负。

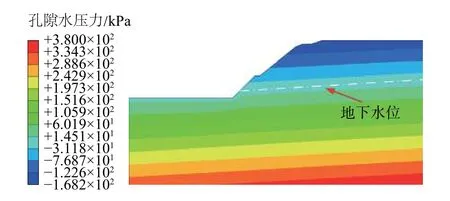
图7 地下水渗流工况孔隙水压力等值云图Fig.7 Pore water pressure contours under groundwater seepage

此工况下当边坡出现塑性区贯通时呈现两道滑动面（图8）。主滑面仍为坡脚贯通至坡顶，但在沿土层分界面出现另一道滑动面，为便于区分，以下根据滑动面与坡面平均距离由深至浅依次称为第一、二、三级滑动面。笔者认为，出现与一般工况单一滑动面不同的二道滑动面的原因一是由于地下水位上下土中有效应力或土的抗剪强度变化规律发生较大变化，二是土中渗透力的影响。与前文图5对比可见，二道滑动面均不呈单一圆弧形，第二滑动面在坡脚以上，但第一滑动面（为已贯通的主滑面）通过坡脚路面以下，然而，即使是较深的第一滑动面，其与坡面的平均深度也浅于一般工况单一圆弧滑动面，表明地下水渗流作用可使边坡由深层滑动模式向浅层滑动模式转化。然而，分析所得地下水渗流作用下该边坡稳定安全系数为1.251，反而较不考虑地下水渗流工况时1.200 有所偏高，笔者认为主要有两方面的原因，一是表1中工勘报告提供的有效应力抗剪强度指标较实际偏高，二是负孔压使地下水位以上非饱和土抗剪强度增大。

图8 地下水渗流工况塑性应变等值云图Fig.8 Plastic strain contours under groundwater seepage

2.4 降雨入渗工况滑动模式分析

在2.3 节基础之上，进一步分析该边坡在降雨入渗影响下的滑动面模式。ABAQUS 中，可通过在入渗边界设置表面孔隙流强度参数来实现降雨工况的模拟[17]。分析过程中考虑降雨强度和降雨历时两个因素，可分别按照长时小雨、长时中雨及短时暴雨等工况进行分析。分析过程中需先消除边坡初始地应力的影响，再在进行降雨模拟分析的同时采用有效应力有限元强度折减法进行分析。

长时小雨工况，即降雨强度为0.25 mm/h，降雨历时72 h（即3 d），分析结果显示（图9），该工况滑动面变化形式较仅考虑地下水渗流工况不同的是除原来的两道滑动面外，新增了一道由坡脚贯通至一级平台的第三滑动面。这是由于在降雨水入渗作用下，原地下水位以上非饱和区土体不仅因含水量的增高自重增加，而且孔隙水压力增大（由负孔压向零或正孔压转变），越接近地表受降雨影响越显著，致使浅表土体抗剪强度降低明显的缘故。与第三滑动面形成相对应的边坡稳定安全系数为1.164，相较于地下水渗流工况下降7.5%。当模型分析接近于不收敛时，第一滑动面亦贯通至坡顶，此时安全系数为1.20。但由于第三滑动面先于第一滑动面贯通，因此，如果该边坡失稳最先必将沿第三滑动面滑出，也表明在长时小雨工况下，路堑边坡具有局部浅层滑动趋势，这与图2该边坡出现浅层滑坡的事故是吻合的。

图9 长时小雨工况塑性应变等值云图Fig.9 Plastic strain contours under long-term light rainfall

相较于一般工况而言，长时小雨工况下，水平位移变化与塑性区变化相对应，在三道滑动面的影响下，水平位移亦呈现出明显的分区形式，即边坡土体位移在一级边坡、土层分界及第一滑动面具有明显的区分，如图10 所示，表明此时除一级边坡坡体具有较大位移外，同时会因下部土体的较大位移引起上部土体产生相应位移。

图10 长时小雨工况水平位移等值云图Fig.10 Horizontal displacement contours under long-term light rainfall

长时中雨工况，即降雨强度为1 mm/h，降雨历时72 h，该工况第三滑动面贯通时边坡稳定安全系数为1.143，较长时小雨工况略有下降，说明降雨历时相同降雨强度越大，边坡稳定安全系数越低，与人们直观判断规律相符。因该工况下滑动模式与长时小雨工况基本一致，不再赘述。

该路堑边坡地处我国东南沿海地区，在雨季或遭遇台风天气时常有短时暴雨。因此，为进一步比较，笔者另假设5 种不同降雨强度与降雨历时工况进行了模拟分析，并将分析所得边坡稳定安全系数一并列于表2。这5 种工况在降雨划分中属于暴雨、大暴雨至特大暴雨级别。由工况1 和工况3 对比中可发现，降雨历时相同时，降雨强度由20 mm/h 提高至40 mm/h，安全系数下降5.3%，而工况3 与工况5 的对比中可知，降雨强度相同时，降雨历时由2 h 提高至4 h，安全系数下降4.3%。因此，可以说降雨强度相较于降雨历时而言具有更大的危害，短时强降雨更不利于边坡稳定[18]。在相同降雨量的条件下，如工况1 与工况5 亦或是工况2 与工况4，不难发现短时强降雨工况安全系数相对较小。上文所分析的长时中雨工况，降雨总量为72 mm，与工况1 及工况5 降雨总量80 mm 接近，但长时中雨工况安全系数1.143 与工况5 的1.140 较一致，表明长时降雨的危害可堪比同等降雨量的短时强降雨，在边坡工程中应引起重视。

表2 不同降雨工况边坡稳定安全系数Table 2 Safety factors of slope under different rainfall conditions

由图11 孔压云图可见，边坡上部负孔压值相较于前文图7地下水渗流工况出现明显下降，最大负孔压位置由坡顶位置向下收缩，即边坡浅表土体达到饱和时，其孔压增大至零，以致浅表土体因有效应力显著下降而抗剪强度降低，致使边坡更易发生局部浅层滑动。且从该图可见，一级边坡坡面处孔压值较相邻处大，这是由于该处雨水入渗、坡体上部排水富集且未能及时排出等原因使得该处孔压值高于同一水平线。5 种工况下塑性区贯通情况均为图12 所示，均在计算不收敛时仅有第一滑动面和不完整的第二滑动面，且与长时降雨工况不同的是，边坡位移并未延伸至上部土体（图13），表明由于上述原因，使得塑性贯通区不仅仅如前文所述由深层转化为浅层，更为重要的是，由原先的整体滑坡转化为集中于一级边坡处的局部浅层滑坡，与工程实际情况更为一致。

图11 工况3 孔隙水压力等值云图Fig.11 Pore water pressure contours under Working Condition 3

图12 工况3 塑性应变等值云图Fig.12 Plastic strain contours under Working Condition 3

图13 工况3 水平位移等值云图Fig.13 Horizontal displacement contours under Working Condition 3

由表2可见，边坡处于工况3 时，即降雨强度为40 mm/h，降雨历时4 h，安全系数并不能满足规范中所规定大于最低值1.10 的要求，因此，有必要对该边坡进行放坡方案优化分析，使其能满足规范要求，确保边坡在最不利工况下仍能保持稳定。

3 放坡方案对滑动模式的影响

下文拟采用两种放坡方案探究在强降雨工况边坡的滑动模式和稳定性，方案1 是保持平台位置不变，根据一级边坡坡率的改变而变动坡脚位置；方案2 是固定坡脚位置，通过削坡改变一级边坡的坡率。两种方案中，二级边坡坡率维持原来设计方案，仅将一级边坡坡率由原来的1∶1.0 分别放缓至1∶1.20 和1∶1.25，降雨工况按上文分析的最不利工况，即工况3 考虑。

当按照方案1 中一级边坡坡率取为1∶1.20 时，边坡滑动面的情况如图14 所示，可见与上节工况3 类似，位于一级边坡内贯通的滑动面仍为最危险滑动面，但此时安全系数为1.152，相较于工况3 的1.091 提高了5.59%，已能满足规范要求，表明放缓坡度可有效提高安全系数。当一级边坡放缓至1∶1.25 时，边坡滑动面的情况如图15 所示，表明边坡不再发生一级边坡内的局部浅层滑动，而是滑面较深的整体滑动，对应安全系数进一步上升至1.161。表明，放缓边坡不仅能提高边坡的稳定性，而且可有效避免降雨工况下发生局部浅层滑塌的风险。

图14 方案1 塑性应变等值云图（1∶1.20）Fig.14 Plastic strain contours of Scheme 1（1∶1.20）

当按照方案2 中一级边坡坡率取为1∶1.20 时，边坡滑动面的情况如图16 所示，可见滑动面形式异于前文，此时存在两道同时贯通的滑动面，一道仍在一级边坡内，另一道主要沿上下两层的分界面。此时安全系数进一步提高至1.178。由上面分析可知1∶1.20 的放坡坡率易致使一级边坡贯通，而此方案中又因削坡作用缩短土层分界面与坡面距离，因此造成两道滑动面同时贯通的现象。当一级边坡放缓至1∶1.25 时，滑动面的情况如图17 所示，与相同放坡坡率的方案1 大体一致（对比图15），仅有较深的整体滑动面，且安全系数为1.203，大于规范中最高规定1.20，相较于上节工况3 提高10.27%。显然，提高效果是明显的。由此可见，设计适宜的放坡坡率不仅是保障工程边坡的整体稳定性的需要，而且是避免降雨等水害条件发生局部浅层滑坡的需要。

图15 方案1 塑性应变等值云图（1∶1.25）Fig.15 Plastic strain contours of Scheme 1（1∶1.25）

图16 方案2 塑性应变等值云图（1∶1.20）Fig.16 Plastic strain contours of Scheme 2 (1∶1.20)

图17 方案2 塑性应变等值云图（1∶1.25）Fig.17 Plastic strain contours of Scheme 2 (1∶1.25)

4 结论

(1) 按国家规范或经常规极限平衡法、总应力有限元强度折减法进行无支护放坡开挖的路堑边坡设计时，其失稳滑动模式常是深层整体滑动。

(2) 当边坡受地下水渗流影响时，有效应力有限元强度折减法表明，边坡内可能出现多于1 个以上的滑动面，但即使是最深的第一滑动面，其位置将浅于总应力法所得的深层滑动面。

(3) 降雨入渗对花岗岩风化层路堑边坡滑动模式和稳定安全系数均有影响。如实例边坡在长时小或中等降雨作用下坡体内出现三道滑动面，且一级边坡内滑动面最先贯通，滑坡模式由深层整体滑动向浅层局部滑动演化，其安全系数也明显减小；在短时强降雨作用下仅在一级边坡内出现贯通的滑动面，即由整体滑动模式完全转变为浅层局部滑动模式，降雨工况越不利表现越为明显，与实际滑坡现象相吻合，且安全系数不满足规范要求，从而从理论上验证了该路堑边坡发生浅层局部滑动的必然性。因此，仅在一般工况下满足规范对于安全系数的要求，并不能完全确保边坡不出现问题，考虑降雨入渗对边坡滑动模式的影响具有现实意义。

(4) 适当放缓坡率可避免在降雨入渗时发生浅层局部滑动，使滑坡模式仍为较深位置的整体滑动，且安全系数可得到有效提高，以满足规范要求。因此，实践中，采用文中方法对设计的类似地层中的路堑边坡事先进行降雨入渗影响下的模拟分析极为必要，将使放坡坡率更为科学合理，可在确保边坡整体稳定性的同时，最大限度降低其发生浅层局部滑动的可能性。

(5) 应该说明的是，文中对于边坡非饱和区土体并未严格采用相应的抗剪强度理论，非饱和区初始负孔压也只是参考相关文献确定的，与实际情况必存在一定差异，如果有非饱和土室内外测试的数据，并严格采用相应的抗剪强度理论进行分析，其定量计算结果必将更为符合实际。但在缺乏非饱和土室内外测试数据的情况下，实例验证表明，文中简化分析方法不失为一种简单实用的方法。