基于卡尔曼滤波的电力虚假数据注入攻击检测方法
王 勇, 武津园, 陈雪鸿, 程彦喆, 刘丽丽
(1.上海电力大学, 上海 200090; 2.国家工业信息安全发展研究中心, 北京 100040;3.东南大学, 江苏 南京 210000;4.华电电力科学研究院有限公司国家能源分布式能源技术研发(实验)中心, 浙江 杭州 310030)
电网具有系统规模大、结构层次复杂、对实时性要求严格的特点。随着电网智能化的发展,电网对信息技术的依赖度逐步提高[1]。传感设备和集成的通信网络使系统具有实时感知、信息服务和动态控制的功能[2]。对现场设备的数据采集与监视控制系统中数据质量的监视和控制,直接影响控制中心的决策[3]。
计算机在促进电力调度、优化决策的同时,其自身的安全漏洞问题也会带来安全威胁[4-5]。文献[6]于2009年首次提出虚假数据注入攻击(False Data Injection Attack,FDIA)。它是一种典型的网络攻击方式[7],通过破坏数据的完整性以干扰决策,成功躲避坏数据检测机制,达到危及电力系统安全的目的。作为针对基础工业控制系统的一种新型攻击方式,其攻击原理、检测算法、防御措施及安全评估方法亟待研究[8-9]。文献[10]提出了卷积神经网络,从网络数据报文中学习入侵攻击特征,进而实时检测虚假数据的注入。文献[11-12]使用支持向量机的方法,将历史数据投影至低维空间,消除了数据之间的相关性,将注入的虚假数据与正常数据分离。上述两种基于机器学习的检测方法可以实现FDIA的检测,但需要一定量的历史数据作为训练样本,且实验的准确性在一定程度上与文献所提出的检测器的训练结果相关。文献[13]提出了基于量测数据相关性和新息图法来检测恶意数据,并对新息图法的应用提出了优化措施。文献[14]提出了基于数据关系图的检测方法,当存在虚假数据注入攻击时,根据状态关系图出现的新的状态节点和分支,判断并识别虚假数据注入攻击的攻击点。上述两种基于图论的检测方法中,文献[13]针对的是传统的不良数据,文献[14]则将图论的方法引入到虚假数据注入攻击中,在生成数据关系图时,仍需要一定量的数据进行预先训练。文献[15]证明了常用的卡方检测器无法检测出隐蔽虚假数据注入攻击,由此进一步提出基于RQ自适应动态估计的卡尔曼滤波器,并对注入攻击提出了检测判断的方法。文献[16]基于扩展卡尔曼滤波的方法,提出了一种针对虚假数据注入攻击的检测方法。上述两种基于卡尔曼滤波的方式可以较好地实现对系统的实时跟踪。本文借鉴了此类思想,搭建了卡尔曼滤波的状态估计器,并改进了检测算法。
本文在电力系统状态估计模型的基础上,分析了虚假数据注入攻击的原理,在IEEE-14节点系统中完成虚假数据注入攻击实验,以验证传统针对不良数据的检测方法的局限性,并设计了一种基于卡尔曼滤波理论的检测方案。
1 虚假数据注入攻击
FIDA是一种针对电力系统状态估计的有蓄谋的一种攻击。
1.1 状态估计模型
以直流模型线性化为基础的状态估计模型可表示为
z=Hx+e
(1)
式中:z——量测量;
H——系统参数矩阵,是常数矩阵,由电力系统的拓扑和线路阻抗决定;
x——有待估计的状态量;
e——测量时的误差。
通过加权最小二乘法(Weighted Least Squares,WLS)或其他算法求解函数得到估计表达式。估计表达式与阈值的关系是衡量系统是否存在不良数据的标准。即
J(x)min=(z-Hx)T·W(z-Hx)
(2)
式中:W——加权矩阵。
测量值中可能带有坏数据。为了避免可能源自故障传感器或拓扑误差等原因的不良测量,需要将J(x)与阈值τ进行比较。如果J(x)小于阈值τ,则认为没有不良数据,反之要剔除相应的坏数据对系统重新进行状态估计。
1.2 攻击原理
上述机制被文献[6]引入FDIA后遭到破坏。该攻击可以躲避残差检测,使状态估计器误认为这些测量数据仍然是好数据,达到操纵状态估计准确性的目的,破坏电网稳定运行甚至从中谋取非法的经济利益[17-19]。
在原始量测量中加入非零攻击矢量a
a=(a1,a2,a3,…,am)T
(3)
导致新的量测量za=z+a产生偏差。za发送到状态估计器将导致状态估计结果带有偏差,即
(4)
式中:c——非零的向量;
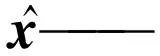
将攻击矢量构造为a=Hc,则
(5)

2 卡尔曼滤波算法
2.1 算法分析
卡尔曼滤波算法是通过系统的输入输出,利用系统状态方程,实现对系统状态最优估计的一种算法[20]。在连续变化且带噪声的系统中运用卡尔曼滤波算法,具有占用存储内存较小、处理速度快等特点,适用于处理实时问题[21]。在已知模型的条件下,由于初始的误差、噪声变化、外界干扰等一些原因,使得输出变量和状态变量存在误差。该算法通过比较对象和模拟系统的输出,将其差值反馈到估计量中,实时修正模拟系统中的状态变量。卡尔曼滤波原理如图1所示。

图1 卡尔曼滤波原理
2.2 状态空间模型
文献[22]的研究表明,电力系统中的攻击或故障总是反映在电压、电流或相位的变化上。文献[23]从三相电压公式推导得到了单测量节点的状态空间模型。本文假设单点攻击,使用单测点模型,动态方程为
x(t+1)=Ax(t)+w(t)
(6)
式中:t——时刻;
x(t)——系统状态,x(t)=[AcosφAsinφ]T;

w(t)——系统误差,满足均值为零、标准差为σ的高斯白噪声。
2.3 算法流程
基于卡尔曼滤波的状态估计器流程如图2所示。

图2 状态估计器结构流程
主要步骤的公式如下。
(1)时间更新
(7)
P(t|t-1)=AP(t-1)AT+Q
(8)
式中:Q——过程噪声;
P——滤波方差值。
(2)量测值更新
(9)
式中:K(t)——卡尔曼增益;
y(t)——电压输出;
C(t)——协方差矩阵。
3 虚假数据的注入检测
3.1 FDIA下的卡尔曼滤波器
FDIA模型为
y=C(t)x(t)+v(t)+λya(t)
(10)
其中λ与攻击位置有关。线路拓扑中存在较为脆弱的节点,在不同位置上的攻击,理论上引发的后果会不同。故在式(10)中引入位置变量,便于对不同脆弱级的节点加以区别。ya(t)表示攻击者构造的攻击向量。当有攻击发生时,测量输出产生变化,量测的变化量再作用到状态估计量中,导致状态估计量也产生偏差。
3.2 检测方法
当无攻击发生时,尽管观测器存在估计误差,但观测值和系统状态在小范围内基本一致;当有FDIA时,检测目标函数f(t)将逐渐增大,并超过一定的检测阈值r。
考虑用如下的目标函数进行检测
(11)

根据检测目标函数与阈值r相比较可知:f(t)≥r,系统存在攻击;f(t) 在IEEE-14系统下进行实验。在没有发生FDIA的情况下,实验结果如图3所示。 图3 没有FDIA时的目标函数 由图3可知,在没有FDIA的情况下,系统不会发生误报,经过4次迭代,目标函数收敛;标准化残差法和目标函数极值法的检测结果中均未显示虚假数据。 利用matpower 4.0仿真数据包中IEEE-14拓扑结构下的潮流数据,修改量测点数值的大小。 此时在1#数据编号位置,注入虚假数据,修改其值为1,检测结果如图4所示。 由图4可知,尽管存在虚假数据,在测量数据编号关于标准化残差和目标函数极值的图中均未显示检测出虚假数据。 图4 有FDIA时的检测结果1 此外,在上述情况下,注入虚假数据的位置不变,修改其值为2,虚假数据注入下的检测结果如图5所示。 由图5可知,在测量数据编号关于标准化残差和目标函数极值的图中均有虚假数据的标注,表示检测出了虚假数据。但是由于攻击设置在1#数据编号位置,测量数据编号关于标准化残差的图中标记在27#位置,测量数据编号关于目标函数极值的图中标记在26#位置,所以仍无法有效且正确地检测出虚假数据注入攻击。 图5 有FDIA时的检测结果2 为验证本文所提算法的可行性,利用MATLAB软件,在三相电压模型上进行仿真实验。仿真实验采用的仿真参数如表1所示。 表1 仿真参数 在没有FDIA时,卡尔曼滤波状态估计器对系统的状态观测结果如图6所示。 由图6可知,尽管输入信号中混有随机高斯白噪声,卡尔曼滤波器仍可以较好地实现对系统的实时状态跟踪。 图6 没有FDIA时估计器对系统的状态观测结果 在0.2 s时触发FDIA,卡尔曼滤波状态估计器对系统的状态观测结果如图7所示。 图7 有FDIA时估计器对系统的状态观测结果 由图7可知,在有FDIA的作用下,卡尔曼滤波器的输出信号出现较大的波动。 在系统没有虚假数据与有虚假数据攻击两种状态下进行检测效果对比,如图8所示。由图8可知:没有FDIA时,尽管存在噪声信号,检测目标函数可以稳定在零附近,不存在幅值上的较大变动;有FDIA时,检测曲线发生明显的变化,并很快超过检测阈值,检测有效。 图8 两种状态下的检测效果对比 本文对FDIA的原理、状态估计的模型进行了分析,对以残差方程为基础的标准残差检测法和目标函数极值法进行了攻击验证;提出了一种针对FDIA问题的检测方法,能够在无需历史数据训练的情况下,短时间内检测到FDIA的发生,并进行了验证。后续考虑进一步提高状态估计器的抗噪能力,并对攻击点进行辨识。此外,对FDIA的研究一直是智能电网领域的重要课题,还有待学者们进一步的探究。4 实验验证
4.1 没有FDIA检测
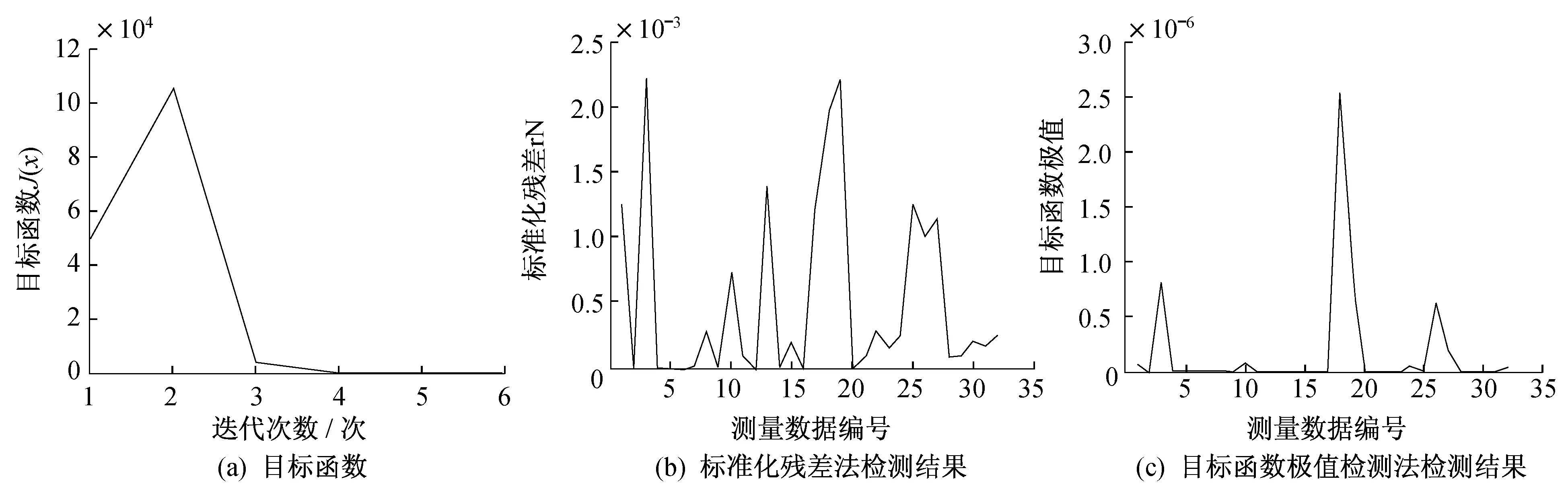
4.2 有FDIA检测
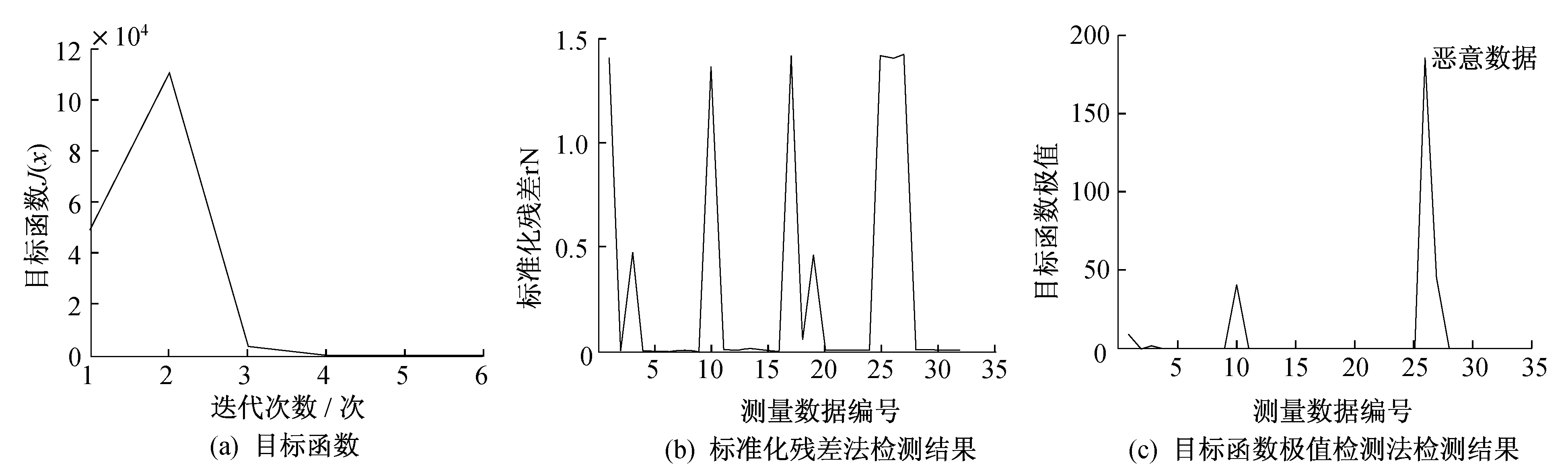

5 仿真分析


5.1 没有FDIA时的状态观测
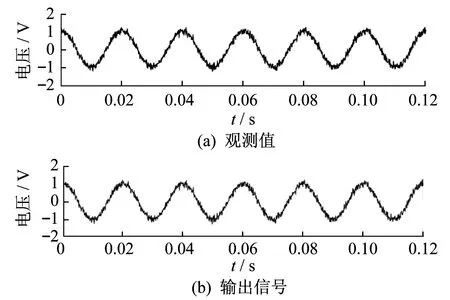
5.2 有FDIA时的状态观测

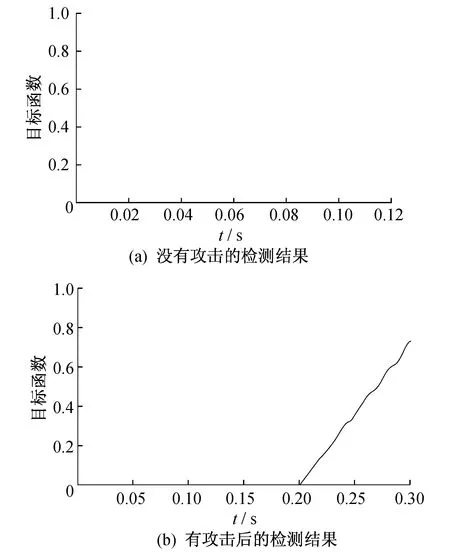
5.3 两种状态下的检测效果对比
6 结 语

