静叶部分间隙对压气机低工况稳定性影响
赵文峰,姜斌,段昱,郑群
(哈尔滨工程大学 动力与能源工程学院,黑龙江 哈尔滨 150001)
对于多级压气机,变工况设计是一项难度很大的工作,角区失速是旋转失速的触发[1-4]。一般将压气机扩稳方法分为主动控制和被动控制2类。主动控制需要外接能源与装置,可以随流场的变化而改变控制状态。常见的主动控制方法有抽吸[5]、尾缘、喷气[6]等,但是由于装备复杂并且需要外接能量,很少在真实压气机上得到应用。被动控制常见手段有弯掠叶片[7]、可调导叶[8]、旋涡发生器[9]等。由于被动控制不需要外接能源与装置,因此作为二次参数扩稳方法广泛的应用在工程上。部分间隙作为一种被动控制手段能够对角区失速有明显改善,在平面叶栅中部分间隙能够消除角区分离,对流场设计点的损失也比整体间隙小[10]。因此本文提出在真实压气机上应用静叶部分间隙,并通过不同间隙的位置对流场的影响来研究间隙对角区失速的控制机理。通过对某自主设计1.5级压气机的不同部分间隙定常数值计算探究间隙位置对压气机低工况的特性与流场影响。
1 压气机数值计算模型
本文研究对象为某8级低压压气机前1.5级,并针对低工况(60%折合转速N)进行拓稳研究。进口总温288 K;井口总压0.1 MPa;转速4 440 r/min;叶片数为进口导叶20;动叶15;静叶18,该转速下最大效率为93.3%,压比1.114。
采用商用软件ANSYS CFX对研究对象进行定常数值计算。湍流模型为SST,进口条件给定总温280 K、总压101 325 Pa。综合考虑计算精度与计算速度,三排叶片网格总数约为241万。图1与图2为所计算模型的整体示意图与网格分布。图3为部分间隙设计方案示意图,所有部分间隙都尺寸参考经验参数[11]。长度为0.06 m(0.5倍叶根弦长),高度为0.9 mm(0.4% 倍叶高)。图4为本文所用计算方法与实验的校核。本文针对根部叶高的压力系数,叶片吸力面表面极限流线以及沿叶高方向的总压损失系数分布进行试验校核。按照实验测得的边界条件进行多次试算,并调整了软件的部分设定,使得计算结果能够很好的和实验结果相对照。图5给出了rotor37[12]的CFX实验校核对比。结果表明,按照以上描述的设定进行数值模拟是可信的。

图1 1.5级压气机计算模型Fig.1 Computational details of 1.5 stages compressor
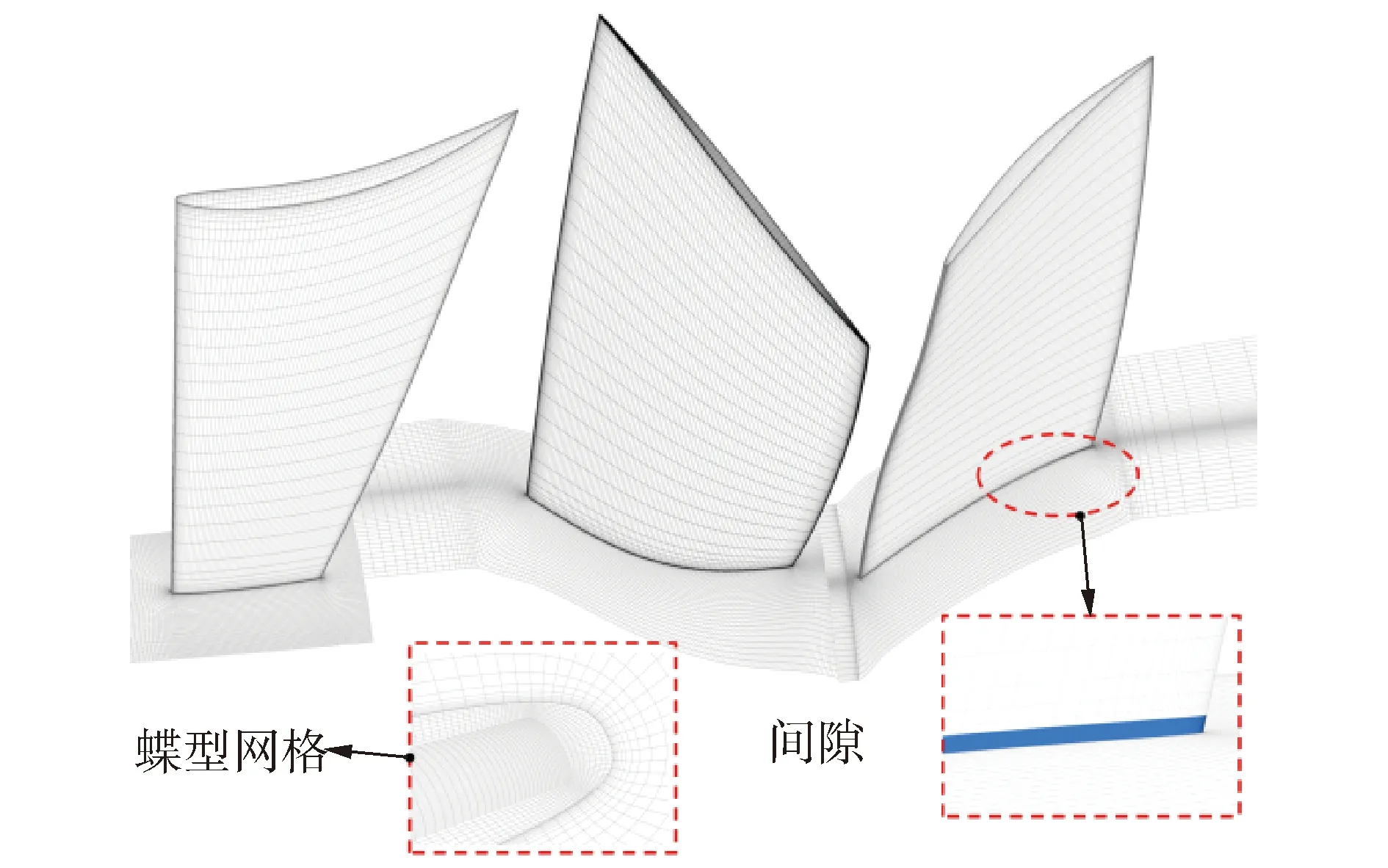
图2 1.5级压气机流道计算网格Fig.2 Computational mesh of 1.5 stages compressor
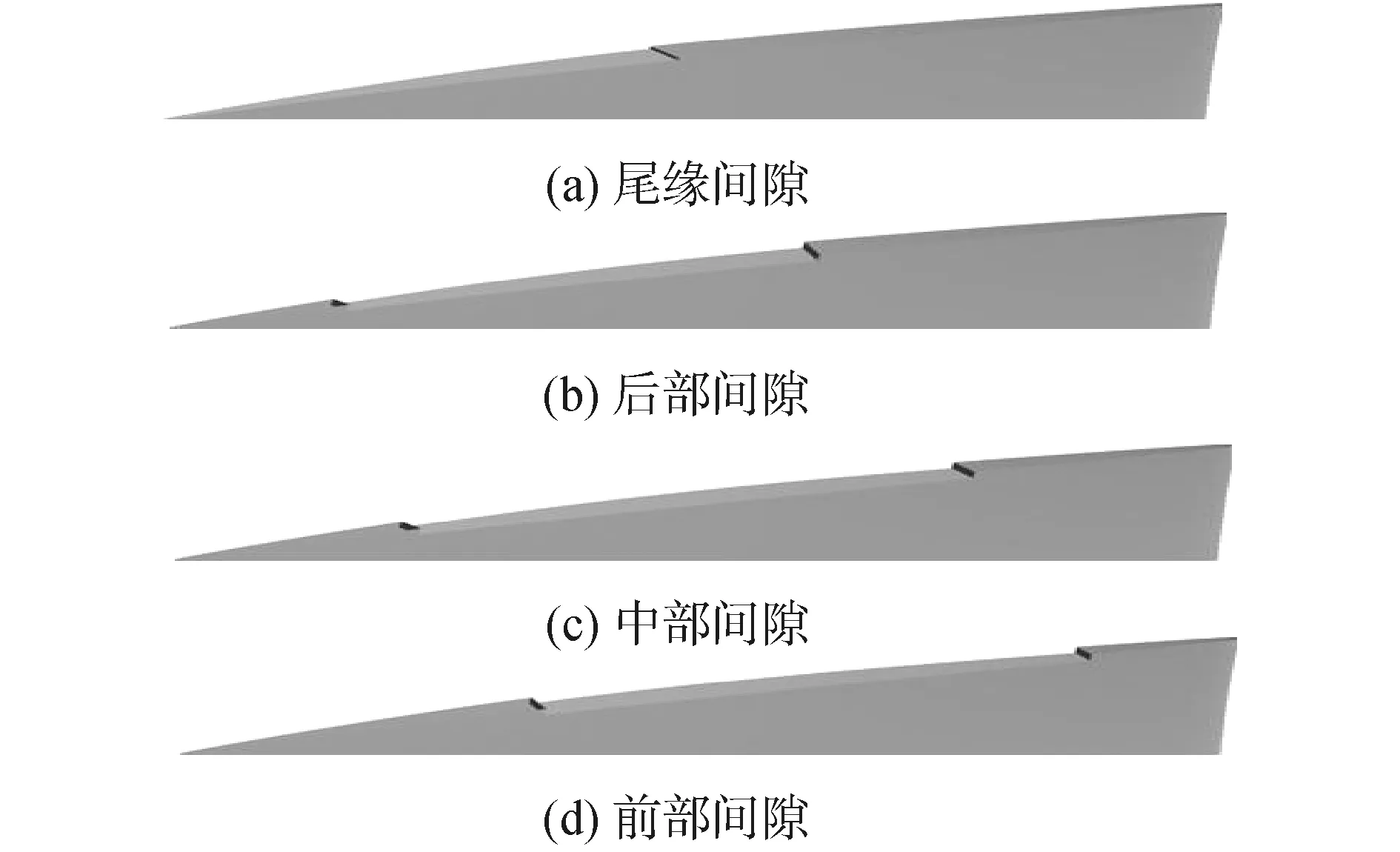
图3 部分间隙方案Fig.3 The scheme of partial clearances
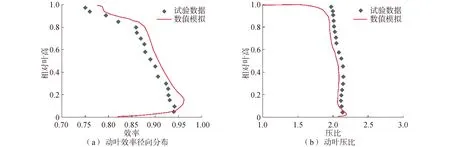
图4 计算方法与rotor 37 试验校核Fig.4 The verification between experimental of rotor 37 and computational methods
2 1.5级压气机部分间隙计算结果与分析
2.1 不同位置间隙对压气机性能影响
原型压气机在0.6N折合转速下,以每一步完整收敛解为初场,逐步提升背压;以发散前最后一个收敛解作为近失速点,以此来获得压气机原型以及不同尾缘间隙下的效率压比特性线如图5。
图5的效率-压比特性可以看出,对于不同间隙,压气机的堵塞流量几乎不变,随着静叶部分间隙位置的向前移。喘振边界的流量点随着不断向左移动,并且裕度不断增大,裕度SM为:

图5 不同间隙下特性Fig.5 Characteristic lines with different clearances
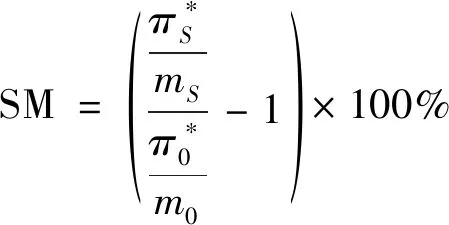
(1)
式中:SM为压气机裕度;m为压气机质量流量;π为压气机总压比;下标0表示工作点,s表示近失速点。
原型压气机裕度计算得到25.4%。通过设置静叶间隙后,从尾缘间隙开始,裕度分别为26.6%、28.3%、30%和34.4%。可以看出部分间隙可以提升压气机低工况裕度,但是间隙向迁移的同时工作点的效率也下降的十分迅速。前缘间隙是牺牲设计点效率换取裕度,因此综合对比之下,中间间隙对流场的改善性能最好。
2.2 压气机近失速点流场分析
在近失速点压气机静叶角区流场如图6所示。从图上可以看出原型压气机在近失速点处发生了角区失速。对于轴流压气机,一般来说气动不稳定主要产生原因有2个方面,叶尖泄漏导致的旋转失速与静叶角区分离导致的角区失速。本文所研究的压气机在60%N转速下动叶叶顶泄漏并没有形成突尖失速。因此本文所用模型在低工况时的失速完全是由静叶角区失稳导致。图中可以看出静叶上部流动相对良好。小的螺旋点是由动叶叶顶尾迹导致,并没有导致叶顶角区失速。

图6 角区极限流线与静压系数Fig.6 The limiting streamlines with static pressure distribution in hub corner
静叶角区下半叶高存在3个明显的闭式分离区域,对应着图中的3个闭式螺旋点N1、N2、N3。轮毂附面层在叶根大攻角流动作用下形成轮毂螺旋点N1,涡核位置在0.5倍弦长。在静熵云图中对应着高静熵集中区。压力面流体流到尾缘受N1的卷吸作用沿着吸力面回流并抬起形成螺旋点N2,但是尺度比较小。同时小尺度螺旋点N2诱导出螺旋点N3,整个流场的流动堵塞以N1为主。N1的径向发展堵塞了静叶角区造成了气动不稳定。因此对于流场的控制应该基于为轮毂附面层低能流体充能。静叶根部设置间隙后,近失速点流场状态发生了改变。
在图6 (b)中,轮毂径向涡与间隙所产生的泄漏流相互作用:一方面,泄漏流所产生的动量流体使得径向涡向尾缘方向迁移和变形。径向涡核从0.5倍弦长迁移到大约0.7倍弦长。同时在泄漏流的冲击下径向涡变的不稳定。一部分流体被冲到尾缘后随着泄漏流的能量减弱在尾缘重新形成了2个由鞍点S1相连的螺旋点N3、N4。这是典型的鞍点螺旋点所形成的闭式分离,具有禁闭性。从熵云图中与原型流场相比,也可以看出静熵集中区(涡核)向后移动,但是新生成的闭式分离导致叶根区域的高熵区域范围扩大,叶根损失增加。同时间隙泄漏在径向涡的作用下分成2部分,一部分被不稳定的径向涡系(N1、N3、N4)卷吸;另一部分在旋涡的旋转作用下被甩进叶片吸力面附面层。从吸力面极限流线中可以看出,与原型相比,吸力面的集中脱落涡因为部分泄漏流的汇入尺度更大。集中脱落涡的径向尺度从0.3H发展到0.5H。虽然尺度增加,但是旋涡强度明显减弱,变现为角区的静压系数明显上升,原型角区的低压区减少,说明间隙泄漏的冲击作用使得旋涡进入不稳定状态。
图6(c)为后部间隙,从极限流线可以看出,尾部间隙所产生的泄漏流具有更强的动量,径向涡在泄漏流的冲击下破碎。在破碎后的小旋涡之间能看到明显的泄漏流冲击轨迹。整个轮毂区由多个破碎后的小旋涡组成。泄漏流在静叶的前缘诱导出新的螺旋点。在熵云图中轮毂的高熵集中区消失,且相对尾缘间隙破碎后的轮毂高损失区域减小。对于吸力面,随着泄漏流的动量增强。集中脱落涡缺乏了来自轮毂附面层的低能流体输运,因此后部间隙的集中脱落涡也不再稳定,尾缘间隙中的整体螺旋结构被破坏。在拓扑上变现为出现螺旋点与鞍点紧密相连的不稳定结构。
间隙位置继续前移为中间间隙图6 (d)。此时泄漏动量达到最大,角区的闭式分离被吹除,从拓扑上看除了间隙前段被泄漏流诱导出现的螺旋点N1。整个轮毂流场中没有其他的闭式分离存在,只有一条间隙泄漏形成的开式分离线L1,同时泄漏的作用抑制了集中脱落涡的形成。吸力面上的螺旋点消失,流动状态得到改善。在熵云图中,前面图6(a)~(c)所存在的大范围熵增区被泄漏涡取代。从整体上看开式分离所形成的泄漏熵增要远小于闭式分离失速涡的熵增,因此可以说这种控制方法是有效的。
在前部间隙图6 (e)中,轮毂流场上径向涡破碎成小旋涡,与后部间隙有些相似,不同的是前部间隙的泄漏动量更强,所形成的小旋涡尺度相比于后部间隙更小。同时泄漏涡的前移使得集中脱落涡重新形成,在熵云图中能明显看出吸力面前缘处出现了高熵区,这是泄漏流与破碎的径向涡所共同形成的。
从0.1倍弦长(0.1C)流面开始综合对比了静叶流道内S3流面的流线分布与相应的旋涡演化规律。选取6个S3流面进行研究,流场结构如图7所示。在S3流面中可以清晰的看出失速涡的径向尺度以及沿弦长的发展情况。原型静叶流场中图8 (a),起始于0.1倍弦长的结点标志着吸力面流动分离的开始(径向尺度为0.1H)。受到下游的角区失速低能流体团的影响,进行展向发展及向压力面迁移,同时在逆压力梯度的作用下结点向螺旋点转变。在0.5倍弦长处转化为完全闭式分离的螺旋点,对应着失速涡的涡核区域。虽然图中并未显示完全,但是在0.9倍弦长流面上出现了明显的鞍点。根据拓扑法则,螺旋点与鞍点总是成对出现可以确定流场中的结点转化为螺旋点。同时可以看出静叶的失速区域在角区径向尺寸约为0.4H。

图7 静叶10%相对叶高静熵云图Fig.7 The static entropy contour at 0.1H of the stator

图8 静叶流通中旋涡发展Fig.8 The process of vortices in the stator passage
图8 (b)为尾缘间隙的S3流面,可以看到叶根0.05H处,一部分流体通过尾缘间隙被卷吸进吸力面,在S3流面上留下了明显的回流涡。起始于0.9C逐渐发散终止与0.5C(涡核处)。由于径向涡没有被泄漏改变,因此图8 (a)中出现的结点迁移与转化在尾缘间隙中依旧出现。由于卷吸作用使集中脱落涡变强因此高熵区的径向尺度略大于原型,这与前文是一致的。图8 (c)为后部间隙,与图8 (b)相比,分离区的高熵区域径向尺度减弱。0.9倍弦长处的鞍点被向后推移至1.1倍弦长处。同时间隙流在0.3倍弦长处诱导出吸力面的输运涡将前缘流体输运到泄漏流中。当间隙位置达到静叶中部时,图8(d)所示能看到整个流场中高熵区明显减少。在0.5倍弦长处间隙泄漏涡开始形成整个径向尺度都没有超过0.05H。可以说中间间隙可以有效的控制角区分离,并在前部间隙图8 (e)中可以看到。其控制效果与后部间隙相似,都能在一定程度上降低高熵区的径向尺度。不同的是,前部间隙所产生的泄漏诱导涡更加靠近吸力面,这是由于更强动量的泄漏涡将诱导涡吹向压力面。值得一提的是对比前部间隙在0.7倍弦长与0.9倍弦长后形成了静熵的突增。前部间隙对尾缘的流场的恶化作用是由叶型弯角引起的。在相同的静叶叶型,间隙位置越向前,所产生的射流相对于尾缘的攻角越大,更加容易引起后方的流动分离,这也进一步解释了前文中前部间隙能更好的拓宽裕度却在设计点造成更大损失的原因。
图9 给出了不同间隙的泄漏流动量,该泄漏流动量的差异是不同位置间隙对角区流场影响效果不同的原因,角区分离/失速产生的主要原因为附面层低能流体不能抵抗流道中横向压力梯度而产生过度折转向吸力面堆积。随着流量的减少,低能流体的轴向动量减弱,当流体不能抵抗流向逆压力梯度时就会产生回流。回流的径向发展形成了角区失速的径向涡,而间隙控制技术的核心思想就是为低能流体充能来抵抗横向和流向压力梯度。因此不同位置间隙控制效果的区别取决于间隙的泄漏动量,此处定义速度与密度的乘积为泄漏动量。分别定义尾缘间隙为1,后部间隙为2,依次向前类推。可以看出间隙前移泄漏动量逐渐增大在中间间隙时泄漏动量达到最大。而前部间隙动量最小。这从机理上解释了间隙位置与控制效果的关联。为了进一步分析间隙对压气机性能的影响,将出口截面数值模拟结果周向平均后得到静叶径向出口参数分布如图10、图11所示。

图9 不同间隙的泄漏流动量Fig.9 The momentum of the leakage flow with different cases
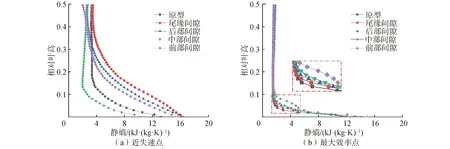
图10 出口截面静叶静熵的径向分布Fig.10 Radial distribution of the static entropy in the outlet of stator
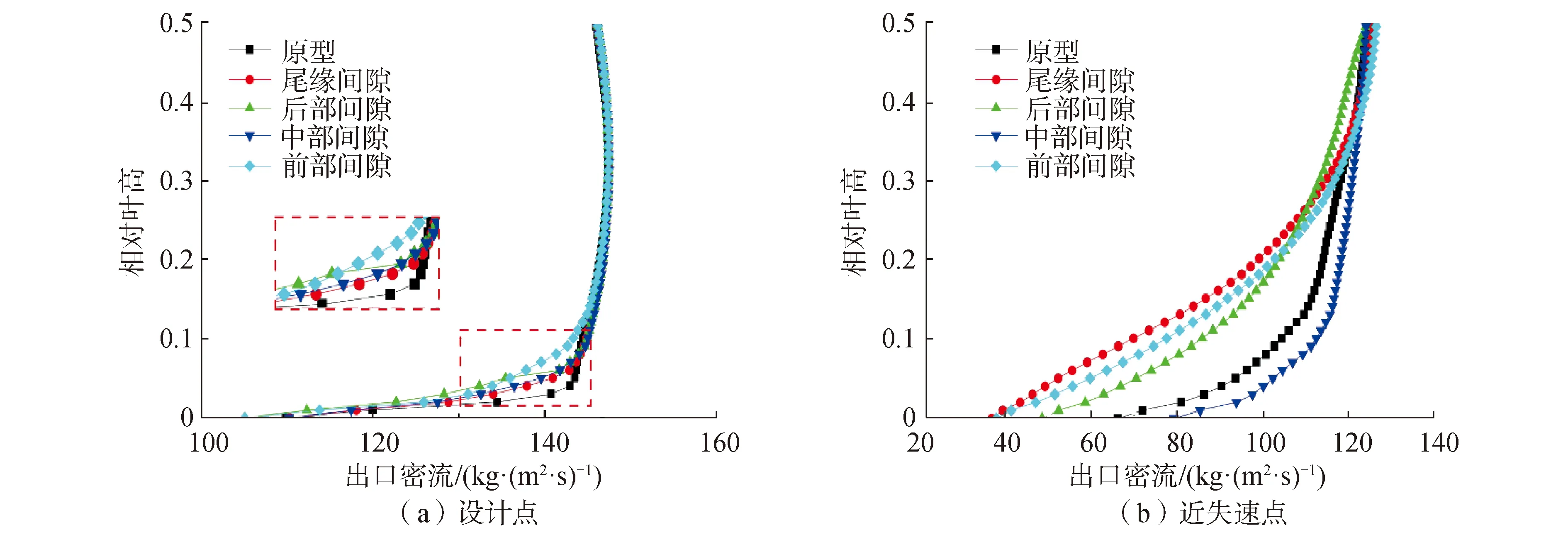
图11 出口密流径向分布Fig.11 Radial distribution of the AVD in the outlet of stator
可以看出在出口截面中间间隙能够有效地降低叶根的静熵;尾缘间隙由于流体被卷吸至吸力面从而使静熵反而更大。对于前部间隙与后部间隙,由于泄漏流将径向失速涡冲击破碎,因此在30%叶高下破碎涡使得静熵高于原型静叶。30%~50%叶高静熵的降低表明间隙可以有效地控制失速涡的径向发展,降低其径向尺度。
一般来说对于被动控制,除了控制效果外,另一个关注点为在设计点的应用,本文用最大效率点来代替设计点。图10 (b)中可以看出所有的间隙都会增大10%叶高之下的流场静熵。但是除了前部间隙外其余位置间隙对叶根的静熵增影响不大。与传统等间隙相比,这种局部间隙控制对设计点损害最小。
角区失速的最大影响后果就是失速流体堵塞流道降低压气机通流能力进而引起发动机失速。因此本文采用轴向密流AVD来衡量出口的通流能力。出口密流表示为轴向速度与密度的乘积。在设计点除了前部间隙,其他间隙对设计点密流影响不大。在近失速点,中间间隙能够有效增大出口密流,增强流道通流能力。这与前面的静熵特征一致。综合静熵与密流的径向分布,可以说中间间隙能在近失速点改善角区失速的同时,对设计点的流场性能影响最小。
3 结论
1) 本文所选用压气机低工况失速原因为静叶角区失速。通过在静叶轮毂角区设置部分间隙可以有效控制角区失速,并且对设计点不会造成大的泄漏损失。
2) 不同位置间隙对流场控制效果不同。尾缘间隙会使泄漏流被卷吸进失速涡从而导致流场恶化,后部间隙与前部间隙所产生的泄漏流与径向失速涡相互作用并导致失速涡破碎。只有中间间隙所产生的泄漏流具有足够动量为附面层低能流体充能从而根源消除角区失速。
3) 静叶间隙是一种有效的角区失速被动控制方法。间隙位置的选取选择在径向分离涡涡核处效果最好,并且此处泄漏流具有最大的泄漏动量。

