多层特征融合及兴趣区域的花卉图像分类

杨旺功，淮永建,2

(1.北京林业大学 信息学院，北京 100083；2.国家林业和草原局林业智能信息处理工程技术研究中心，北京 100083)

基于机器学习的植物图像分类方法克服了人工分类方法的局限性。传统细粒度分类算法，采用尺度不变特征变换(scale invariant featuretrans form，SIFT)[1]或方向梯度直方图(histogram of oriented gradient，HOG)[2]提取局部特征手段，利用局部聚集描述符向量(vector of locally aggregated descriptors，VLAD)[3]或Fisher vector[4]等编码模型进行特征编码。张娟等[5]按照纹理、形状、颜色等手工特征对梅花进行分类，方法不具有通用性。Nilsback等[6]提出了基于花卉几何形状的自动分割算法。周伟等[7]提出了基于显著图的花卉分类算法，为避免分割的依赖关系，将显著图融入特征提取过程，融合颜色和尺度不变特征变换，并采用支持向量机(support vector machines,SVM)进行分类。主流细粒度分类方法基于卷积神经网络[8-12]。本文提出了基于多层特征融合及兴趣区域的花卉图像分类方法。该方法基于VGG16[13]框架，提出基于兴趣区域的特征强化算法，抑制无效信息区域，强化细微特征提取。融合多层网络特征图，采用全局平均池化取代全连接层[14]达到降维目的，从而防止过拟合。采用改进的损失函数pre_softmax完成分类任务，提高了训练网络的识别率。

1 图像预处理

使用深度学习进行图像分类任务时，要求输入的图像尺寸固定，采用图像缩放的方法直接将图像缩放至神经网络可输入的图像尺寸。图像的宽高不等，导致图像不同程度的变形，有效形态特征信息被压缩，从而引起图像细节信息损失，影响图像的分类结果。为了强化图像有效信息，抑制边界信息的干扰，提高神经网络模型的泛化能力，本研究针对花卉的特性，设计的图像预处理流程如图1所示。

图1 图像预处理流程Fig.1 Process of image preprocessing

1.1 图像剪切算法

由于花卉数据集图像的长宽并非全部相等，若采用非等比率缩放图像，会导致图像变形，导致识别目标的细粒度特征变形，从而影响模型的性能。若采用按最短边截取的方法使用图像，相对于模型训练阶段，自动抛弃未被截取的图像信息，影响模型的泛化能力。在模型训练阶段，需要更有效的利用细粒度特征信息；在测试阶段，需要准确截取图像中具有细粒度特征的部分。本研究采用分而治之的策略，训练阶段采用随机截取函数截取图像；测试阶段采用中心截取函数截取图像。这样在模型阶段具有数据扩充的功能，在测试阶段具有识别目标精准定位的作用。截取函数的关键算法如图2所示。

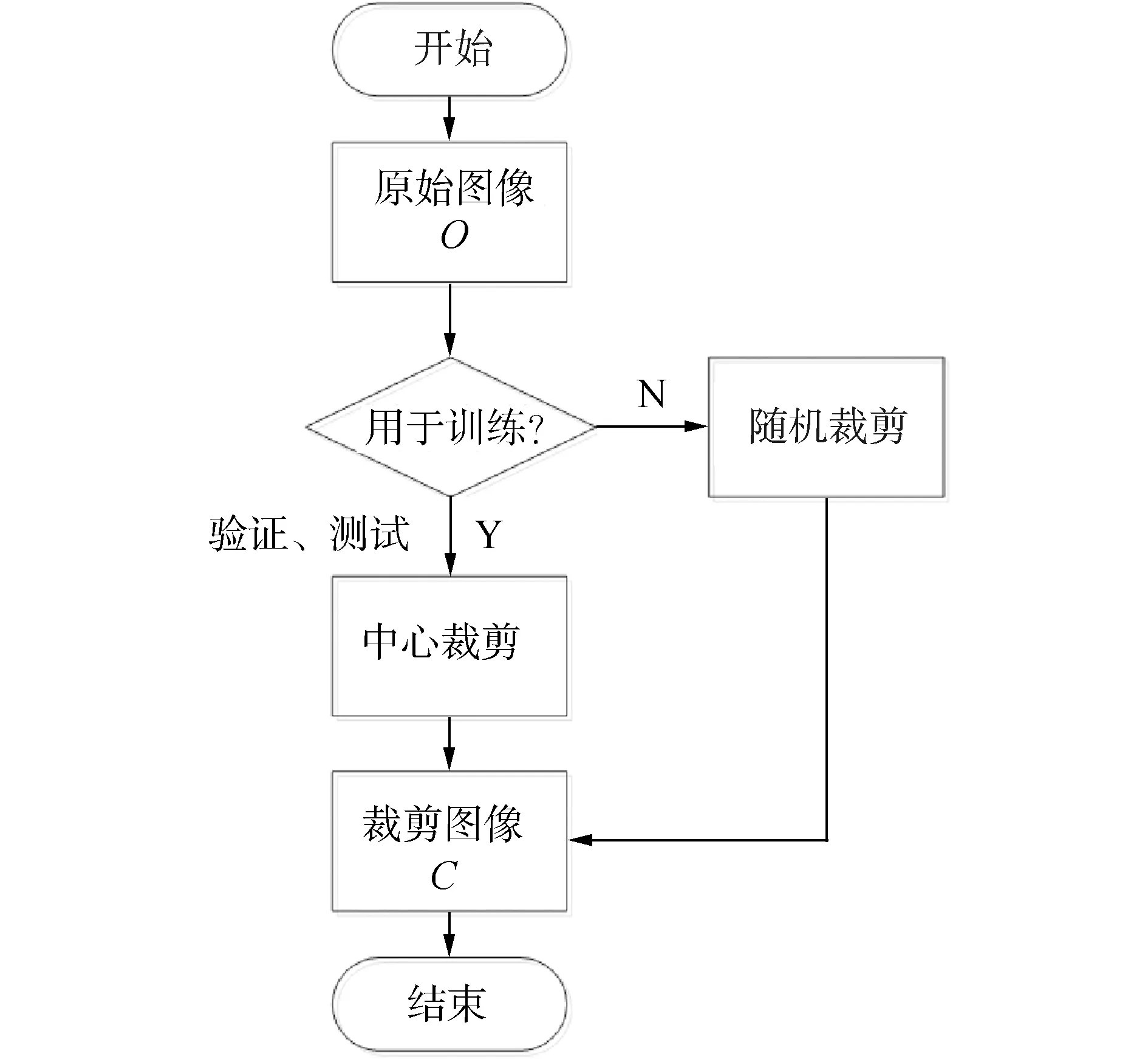
图2 图像截取流程Fig.2 Flow chart of image clipping

中心剪切是在图像的中心位置以原图像宽、高的最短边，截取正方形图像。中心剪切可以获取花卉图像的主要信息，用于模型验证和测试阶段。

(1)

式中：函数box是对原图O截取子图，其4个参数分别表示子图左边界距原图左边界的距离、子图上边界距原图上边界的距离、子图右边界距原图左边界的距离、子图下边界距原图上边界的距离。

随机剪切是在图像区域范围内，按正态随机概率分布的形式，截取以原图像短边长度为边长的正方形图像。随机剪切可以有效丰富图像信息，提升训练模型的泛化能力，其数学表示为：

(2)

式中：frandom(x)表示可产生[0,x]随机数的随机函数。具有识别度的有用信息通常位于图像中间，背景及无用信息位于图像边沿。为了强化图像中间的有用信息，抑制原始图像中的边缘背景信息和噪声信息，frandom(x)采用符合正态分布概率的随机生成函数。

1.2 插值及图像归一化

深度学习的图像预处理常采用图像缩放的方法。图像缩放过程中需要使用使用插值算法来确定坐标像素值。常用的插值算法有最近邻插值、双线性插值、双立方插值、Lanczos插值算法等。相比较而言，最近邻插值算法效率最高，效果最差；双立方插值和Lanczos插值算法的效果较好，但比较耗时。双线性插值算法是性能和效果介于中间的算法。本研究从性能和效果上综合考虑，采用双线性插值缩小图像。图像归一化处理可使得神经网络最优解的寻优过程更加平稳，更容易收敛于最优解。图像归一化处理最常用的是最大最小值归一化[15]方法。计算过程是将原像素值[0,255]进行线性变换，使结果落到[0,1]：

(3)

式中xi表示图像像素值。

2 基于多特征融合的分类方法

基于多层特征融合的花卉细粒度图像分类是基于VGG16的结构，增加了block5_rio和GAP层。block5_rio层是对block5_conv2特征图的判别性区域的提取和强化。block5_rio与block5_conv2维度保持一致。通过全局平均池化的方法对block5_pool和block5_rio降维，并将二者融合拼接成新的张量，再使用1 024个节点的全连接层，通过opt_softmax损失函数分类。基于多层特征融合及兴趣区域的花卉细粒度图像分类系统结构如图3所示。

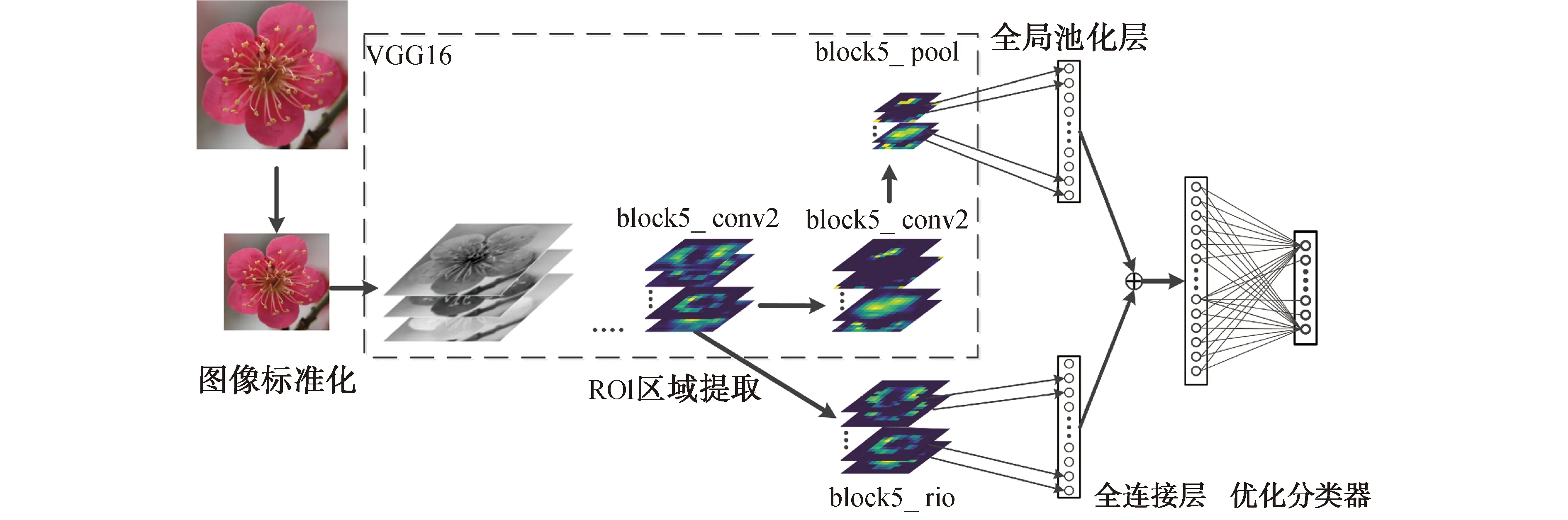
图3 多层特征融合网络总结构Fig.3 General structure of multi-layer feature fusion network

2.1 特征图分析

卷积神经网络由多个卷积层和池化层构成。每个卷积层包含若干个卷积核，经由这些卷积核进行从左到右，上从往下进行卷积运算，得到的数据称为特征图。卷积神经网络的特征提取过程保持着图像的空间结构，即特征图与原始图像在空间上保持对应关系。

池化层是对卷积层的特征图以某种方式进行压缩，缩小特征图的维度、降低网络复杂度，使得神经网络具有更高的鲁棒性，防止过拟合现象。池化层是仿照人的视觉系统处理信息的抽象过程，降低特征维度，并够保留显著信息，从而增加了卷积核的感受野。池化层的特征图与上一层的卷积层特征图的抽象信息保持一致，如图4所示，block5_pool与block5_conv3特征图的信息保持一致。

为了更好理解卷积神经网络的特征提取的特点，本文通过可视化的方法对不同的卷积层和池化层的特征图进行可视化。图4是VGG16的部分卷积层和池化层的特征图叠加可视化效果。

图4分析可知，随着网络层数的增加，特征图的分辨率越小，对图像的抽象能力越高。浅层特征提取的是纹理、细节特征；而深层特征提取的是轮廓，形状，更显著的特征。相比较而言，浅层特征包含的细节信息更多，也具有一定类别区分的能力；深层特征具有判别性，具有明确的分类的能力。以深层特征的分类能力为基础，辅以浅层网络的细节特征，有利于提高分类任务的准确率。

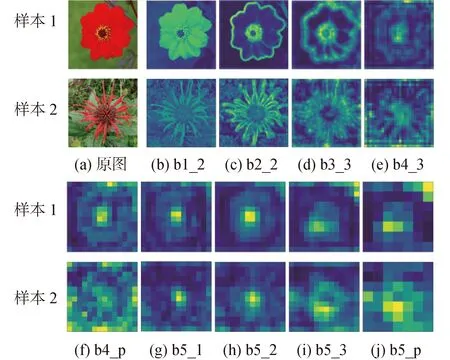
注：b2_2表示block2_conv2卷积层，b5_p表示block5_pool池化层。图4 VGG16网络层特征图可视化Fig.4 Visualization of feature maps in VGG16 network layers

2.2 兴趣区域提取

训练神经网络的过程就是训练卷积核参数的过程，是图像特征不断提取的过程。神经网络越优秀，卷积核的特征提取能力越强。通过神经网络提取出的特征越重要，其连接权重越大，表现为强激活区域。图5是本文所设计的多层特征融合网络特征图的部分强激活区域可视化。

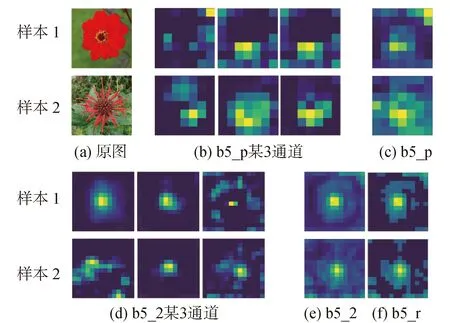
注：b5_2表示block2_conv2卷积层，b5_p表示block5_pool池化层，b5_r表示block5_roi自定义层，其他简称类似。图5 block5_conv2和block5_pool部分通道、及高响应区域特征图可视化Fig.5 Visualization of partial channel and feature maps of block5_conv2,block5_pool and high response area

相较于池化层block5_pool，其他层特征图的抽象性较低，为了提升其他层信息表达能力，本文设计了兴趣区域层，用于强化关键特征。block5_roi层是对block5_conv2特征的提取，并对特征图的强化，抑制背景及噪声干扰，具有提取关键特征的能力。此法可充分融合多层的不同特征，提升网络性能。block5_roi的特征图大小是14×14×512，与block5_conv2保持一致。

为了尽最大可能提取关键区域特征，强化block5_conv2和block5_pool层特征融合效果，将在block5_conv2的特征图中提取兴趣区域。block5_conv2的输入为Iinput：

Iinput=Finput(x,y,z)，1≤x,y≤W，1≤z≤c

(4)

式中：Finput为c表示特征图的通道数。输出定义为Ioutput：

Ioutput=Iinput·Imask

(5)

式中：·表示逐位相乘；特征图的长、宽及通道数保持不变；Imask表示矩阵蒙版，用于截取兴趣区域。

所有通道叠加的平均值称为特征图叠加平均图，记作Istack。与特征图相比，长宽保持不变，通道压缩为1，可表示为：

(6)

Istack特征图叠加平均图的所有像素点的平均数为：

(7)

Imask矩阵蒙版的切片，即单层蒙版可记作Islice为：

Islice=Fslice(x,y) 1≤x,

(8)

Imask矩阵蒙版与蒙版切片Islice的关系为：

Imask=Fmask(x,y,z)，1≤x,y≤W;

1≤z≤C=Islice(x,y,z)，1≤z≤C

(9)

式中Imask是Islice堆叠C次张量，其张量的形状为(W,W,C)。

2.3 全局平均池化及优化损失函数

用传统全连接层连接特征图层，会产生庞大的参数，不可避免导致过拟合现象。GAP层将特征图的每一个通道与GAP层的点相对应，从而赋予通道的意义[14]。因此，在特征图之后，使用GAP代替全连接层，可以将特征图与分类的关系更加清晰，还能大幅降低参数，防止网络过拟合。

softmax函数是logistic函数的扩展。logistic函数只能处理二分问题，softmax可以处理多分类任务，其输出是每一个类的概率值。每一个样本对应的k个概率估计值为式：

(10)

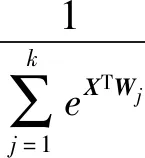
神经网络的训练过程是损失函数寻找最优解的过程，使得损失函数达到最小值。softmax损失函数为：

(11)

在神经网络输出层选用softmax分类函数，其采用交叉熵作为损失函数。由于其计算分类的结果非0即1，必然会引起过拟合，而实践中又无法设置阈值。为了防止过拟合，本文提出了联合样本均匀分布的交叉熵损失方法。样本均匀分布的交叉熵损失Lmean为：

(12)

式中：m表示训练样本的数量;xi∈Rd表示第i个训练样本;yi表示xi的标记。联合样本交叉熵损失与均匀分布交叉熵损失作为总损失：

L=(1-λ)S+λmean

(13)

式中：LS表示softmax 损失；Lmean表示均匀分布的交叉熵损失；λ表示用于平衡2个损失函数的系数，本文中λ取值为0.1。

3 花卉图像分类实验及分析

本研究采用Oxford Flowers 102数据集[6]和Plum Flowers 17。后者是为研究梅花细粒度分类所采集梅花图像数据集，包含17个梅花品种。

本研究的实验电脑配置为PC Intel(R) Core(TM) i7-6700 CPU@3.40 GHz的CPU、8 GB的Nvidia Geforce GTX 1070 GPU和16 GB的运行内存。所有的程序均是由Python语言编写并调用CUDA、Cudnn、OPENCV库并在Windows10系统下运行。

为了保持实验评价标准的统一性，将数据集分为训练集、验证集和测试集按70∶15∶15随机划分。训练时所有模型的优化器采用Adam，批样本数量设置为64，并且都设定了学习率10-3，学习率衰减10-9，每次训练50轮。防止过拟合，实验采用EarlyStopping方法记录到目前为止最好的验证集精度，当连续10次Epoch没达到最佳精度时，则可停止训练。

3.1 数据增强效用评价

为了消除其他因素影响，本实验使用block5_pool层提取的特征，采用VGG的标准降维方法Flatten，连接有1 024个点的全连接层，输出层的激励函数采用softmax。

图像输入给神经网络之前，需要对其进行尺寸归一化操作。传统方法是将图像直接压缩为输入图像尺寸，为了防止训练的过拟合，会采用数据增强技术。实验的数据增强方法采用水平翻转图像、图像归一化处理等操作。为了预防直接压缩而引起的细粒度信息的丢失，本文提出了一种图像预处理方法，防止破坏图像的细粒度特征。为了比较直接压缩、本文图像处理及数据增强的影响，本阶段设计4个子实验，分别是直接压缩、直接压缩+数据增强、本文图像处理、本文图像处理+数据增强。在Oxford flowers 102上的数据增强效果评估实验结果如表1所示。

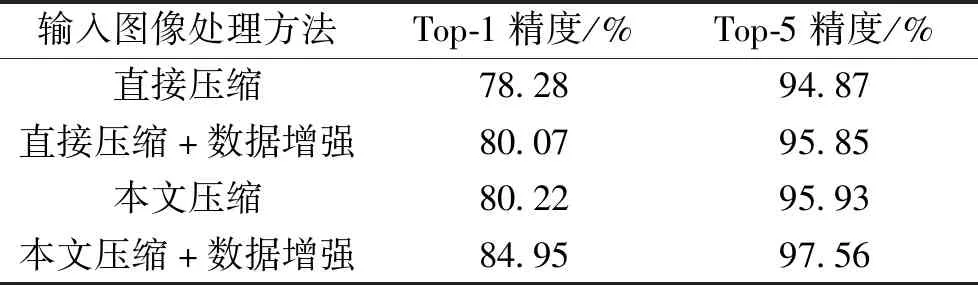
表1 本文压缩方法及数据增强对准确率的影响Table 1 Impact of compression method and data augmentation on accuracy

由表1可以看出，比较Top-1的结果，以直接压缩的方法作为基准，本文图像处理方法对于分类准确率提升明显。本文图像处理+数据增强的分类精度最好，Top-1是84.95%。

3.2 全局池化层效用评估

全连接层致命的弱点是参数量过大，尤其是与最后1个卷积层相连的全连接层。全连接层增加网络训练和测试的计算量，并且由于参数量大，容易引起过拟合。为了比较压平操作和全局池化的差异，本阶段设计2个子实验，在Oxford flowers 102的实验结果如表2所示。

表2 压平操作与全局池化比较实验Table 2 Comparison experiments of GAP and Fllaten

本实验使用block5_pool层提取特征，降维方法分别使用压平操作和全局池化，连接有1 024个点的全连接层，输出层的激励函数采用softmax。

如表2所示，采用压平操作方法的训练参数是25 795 686，全局池化的可以训练参数只有629 862，不可训练参数相同，都是14 714 688。由于压平操作方法的训练参数大，最终的模型文件大小为351 MB，远远超过全局池化方法的模型大小63.4 MB，并且在识别率上，全局池化的识别率明显高于压平操作。实验表明，全局池化取代与最后一个卷积层相连接的全连接层，有效地解决参数过大引起的过拟合问题。

3.3 特征融合评估实验

不计最后3层的全连接层，VGG16包含16层。整体结构上包含5组卷积层，卷积层之后连一个最大池化层，池化层的特征图是对上一池化层的压缩，特征信息保持一致。训练神经网络的过程就是训练卷积核参数的过程，是图像特征不断抽象的过程。为了提升分类准确率，多层特征融合时，对特征图的选择尤为关键。随着网络层数的增加，特征图的分辨率越小，对图像的抽象能力越高，block5_pool必不可少。浅层特征提取的是纹理、细节特征，block5_pool特征的基础上融合其他层的特征提升了效果，需要通过实验验证。本实验分别采取5组卷积层的最后一层卷积层与block5_pool融合训练。由于高层的抽象能力强，识别率高，还开展了block5_conv1、block5_conv2与block5_pool融合的实验。图6是VGG16多层特征融合在Oxford flowers 102上的实验结果。

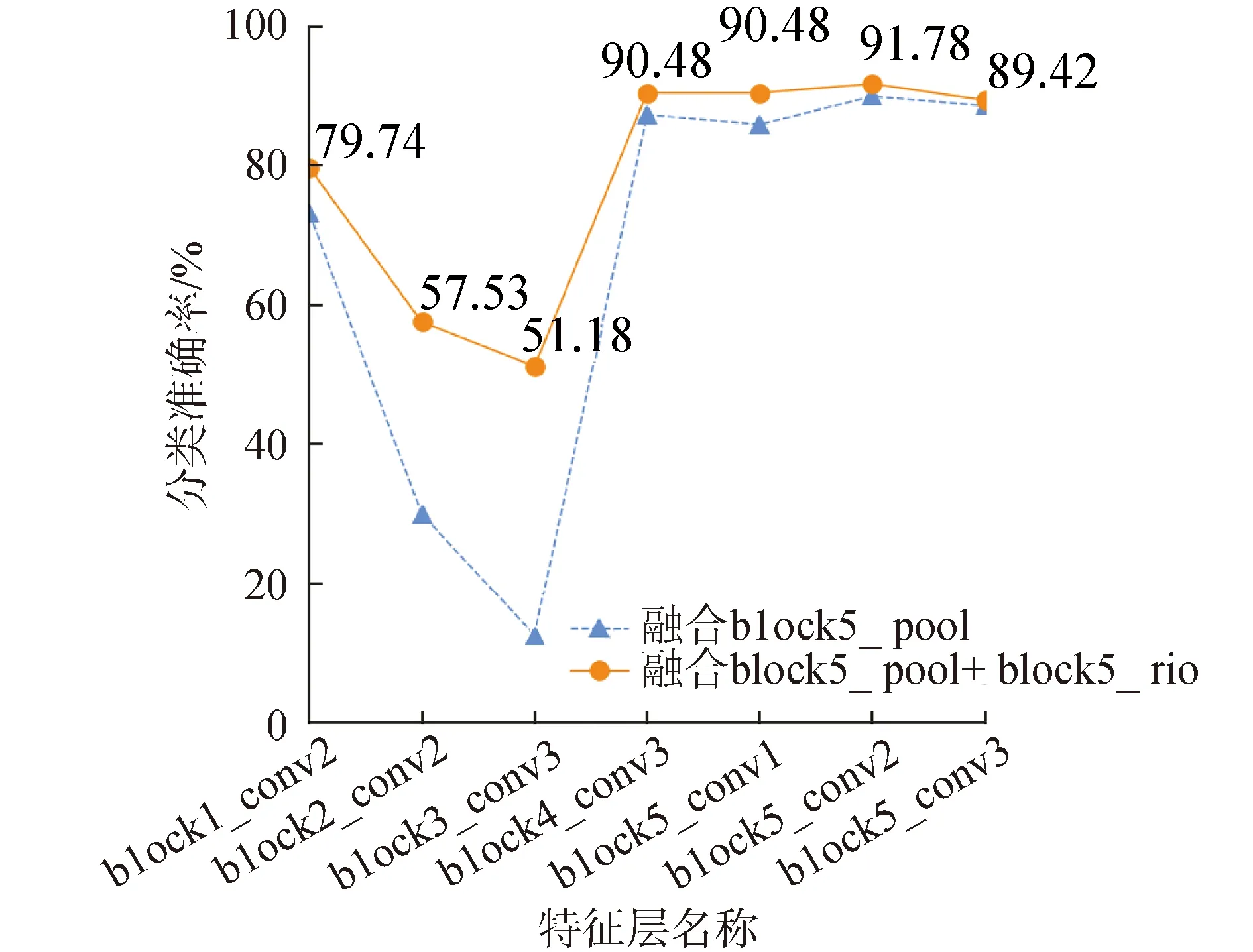
图6 VGG16 block5_pool与其他层特征融合实验Fig.6 Multi-layer feature fusion experiment of VGG16

本实验使用block5_pool层融合其他层的特征图，采用GAP降维，然后连接有1 024个点的全连接层，输出层的激励函数采用softmax。

图6可见，添加了block5_rio层的融合效果较佳，并且block1_conv2、block2_conv2、block3_conv3与block5_pool的融合严重影响基准识别率，不及单独使用block5_pool的识别率88.60%。block4_conv3、block5_conv1、block5_conv3与block5_pool的融合都能够提升图像的分类准确率。在此基础上添加了block5_rio，block5_conv2+block5_pool的融合效果最理想，分类准确率达91.78%。

3.4 优化损失函数评估实验

为了提升分类效果，提出联合均匀分布的交叉熵损失函数。为了对比优化函数的有效性，开展了softmax损失函数与本文优化损失函数的比较实验。

实验使用block5_conv2、block5_pool特征图，并分别使用GAP降维，将降维后的2个张量融合，然后连接有1 024个点的全连接层，输出层的激励函数分别采用softmax和opt_softmax方法。联合交叉熵损失函数在Oxford flowers 102上的实验结果如图7所示。

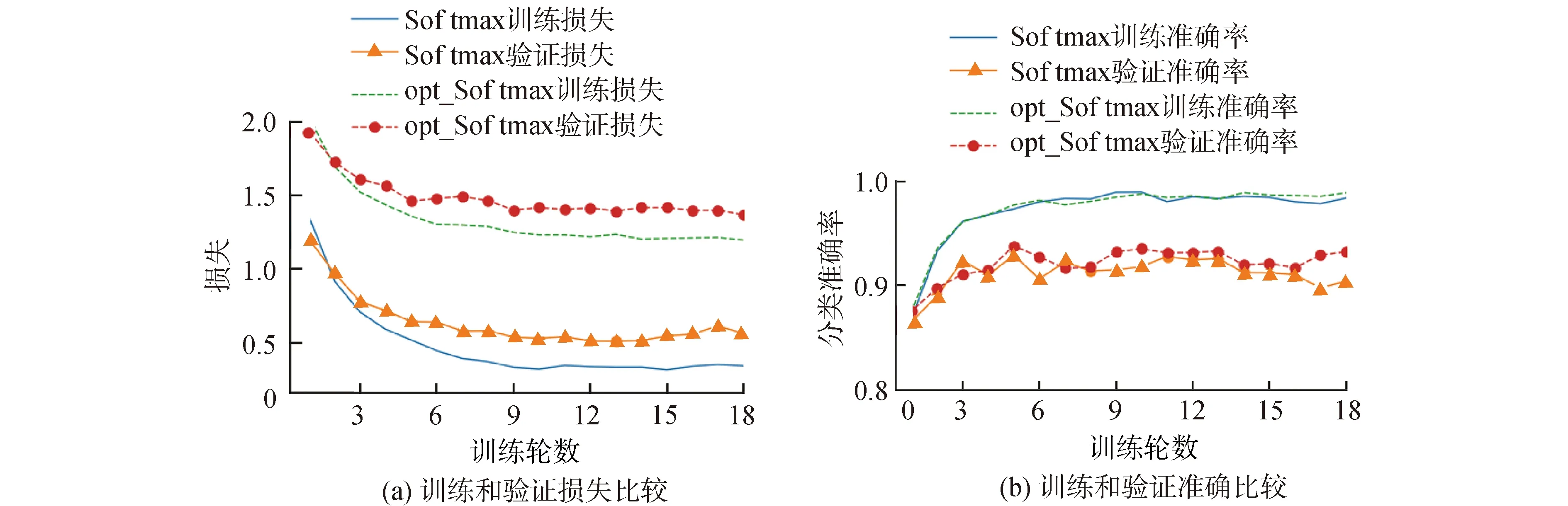
图7 优化损失函数比较实验Fig.7 Comparative experiment of optimized Loss Function

本文提出联合均匀分布的交叉熵损失函数opt_softmax可以缓解传统采用交叉熵损失函数softmax过于自信而导致的过拟合问题，测试准确率从91.78%提升到93.57%，表现良好。

未经过融合的VGG16分类精度只有80.07%。其他研究的分类准确率分别为72.80%[6]、79.10%[15]和84.02%[16]。借助本文提出的图像预处理方法、多层特征融合、及损失函数优化都提升了花卉图像的细粒度分类精度，达到93.57%。

3.5 梅花品种分类实验

上述实验已证明本文提出的多层特征融合细粒度分类方法的有效性。最后将该方法应用于梅花品种数据集Plum Flowers 17进行实验。VGG16的实验采用数据增强，使用Fllaten连接block5_pool，和softmax分类器进行实验。本文采用block5_pool和block5_conv2多层特征融合细粒度分类方法，结构如图3所示。

VGG16和本文方法在梅花数据集上的分类准率分别为71.22%和85.47%。实验结果表明，本文提出的基于多层特征融合的分类方法，不仅适用于标准花卉数据集，还适应于梅花数据集，对分类性能提升明显，因此该方法针对小规模花卉分类具有参考价值。

4 结论

1)本文提出的图像预处理方法，能够防止直接压缩图像引起的破坏图像细粒度特征，有利于神经网络提高分类准确率。

2)多层特征融合方法充分融合浅层特征包含的细节信息，深层特征包含的抽象信息，对分类准确率提升有益。

3)全局池化层替代Flatten层方法降低特征图的维度，使特征图与分类的关系更加清晰，还大幅降低参数，防止网络过拟合。

4)联合均匀分布的交叉熵损失函数可以缓解传统交叉熵损失函数过于自信而导致的过拟合问题。