科技创新对海洋经济发展空间效应的测度——基于多种权重矩阵的实证

狄乾斌，徐礼祥

（1.辽宁师范大学海洋经济与可持续发展研究中心；2.辽宁师范大学地理科学学院，辽宁大连 116029）

21 世纪以来，中国海洋产业快速发展，海洋产业产值连年递增，已成为经济发展的重要引擎［1］，同时党的十九大报告明确提出要加快海洋强国建设，经略海洋、深耕“蓝色国土”，培育经济发展新动能［2］。但近些年来，随着中国经济转入中高速、高质量发展，海洋发展方面很多问题开始暴露出来：海洋产业落后，对海洋资源需求大，导致海洋资源过度消耗；企业配套治理污染设备缺失，环保意识不强，近岸海洋污染严重；海洋技术创新效率不高，创新转化为经济效益动力不足等［3］。在此背景下，重构动力机制，实现高质量创新增长成为中国海洋经济发展的必然选择。经济持续增长的动力来自于技术进步，在加速科技和创新的基础上来发展经济，是刺激经济发展、取得经济增长的主要手段［4］。因此，通过对海洋科技创新效率的测评以及对海洋经济的空间效应分析，掌握区域创新水平对海洋经济的影响状况，进而推动海洋经济在发展新常态背景下朝高效、高质量创新方向发展十分重要。

1 文献综述

关于科技效率对经济发展影响的研究，国外学者的研究开始较早，如Stokey［5］早在20 世纪就对经济增长收敛原因中的科技进步开展研究，提出科技进步收敛性的存在是深度分析经济增长的关键，也是经济增长理论长期研究的热点；Tybout［6］分解了57 个国家的技术进步要素，利用数据包络分析法（DEA）分析全球经济的趋同趋势，认为各国的科技创新和资本积累的差异可能是全球经济两极分化的重要原因。

关于海洋方面科技效力的研究，Brun 等［7］基于1981—1998 年的面板数据对中国沿海和非沿海地区之间的科技创新溢出效应进行了测算；Tingley 等［8］利用随机前沿模型和DEA 方法对英吉利海峡渔业生产的技术创新效率进行了测评，并对其影响因素进行探讨。

国内对海洋科技效率及空间效应测评的研究开始较晚，但发展十分迅速。21 世纪初，庞瑞芝［9］采用DEA 方法对国内主要港口1999—2002 年的经营效率进行测算和评价；戴彬等［10］在采用随机前沿模型对国内沿海11 个省份海洋科技生产率指数测算的基础上，从时间和空间两个维度对海洋科技演变格局及影响因素进行了分析；闫实等［11］基于序列DEA 的超效率SBM 模型对海洋科技创新效率进行了测算，在此基础上，通过空间差异、空间极化和空间聚类刻画海洋科技创新效率空间格局。

从研究现状来看，研究者们多采用传统的DEA方法或改进后的DEA-Tobit 方法、两阶段DEA 方法等对海洋科技的效率值进行测算，没有充分考虑到环境因素和随机因素对海洋科技创新效率值的影响；同时，在研究视角上，越来越多的学者开始关注海洋科学技术在地理空间距离上的相互作用，计量方法也被广泛运用到各种海洋效率测算研究中，在空间层面上推动着海洋研究的发展。基于此，本研究采用三阶段DEA 方法对中国海洋科技创新效率进行测算，并构建多个权重矩阵，通过空间计量模型分析海洋科技创新效率及其他影响因素对海洋经济发展的推动作用，并提出相应的对策和建议，以期为中国海洋经济实现高质量增长提供参考。

2 模型选取和指标选取

2.1 三阶段DEA 模型

数据包络分析方法及其模型由美国著名运筹学家Charnes 等［12］提出，在效率的定量分析上被广泛运用。但此方法将研究对象中的投入和产出视为一个不受外界影响的系统，也没有考虑外部环境因素、随机误差等对研究对象效率值的影响［13］。而社会活动总是产生于一定的地理空间，区域创新系统的绩效不仅受到系统本身的影响，周围环境要素也会对其产生作用［14］。就此，Fried 等［15］提出三阶段DEA，利用随机前沿模型剔除了测算过程中环境因素和随机误差的影响，从而保证了测算结果的准确性。

2.2 空间计量分析

空间计量经济学理论认为，各地理空间单元上的现象并非孤立存在，而是与其邻近地区空间单元上同一现象相关［19］。在使用三阶段DEA 方法测算出海洋科技创新效率值后，为进一步探讨海洋科技创新与海洋经济发展之间的关系，本研究从地理空间的角度对海洋科技创新效率值和海洋经济发展水平进行计量分析。

2.2.1 空间权重矩阵的构造

区域之间的空间联系常采用空间权重矩阵来度量，邻接权重矩阵在既有的空间计量分析研究中最为常见［20］。但区域之间地理联系明显不局限于地域相邻，且除了地理上的联系，沿海各省份之间还存在各种经济社会关系。因此，为更好地刻画研究对象的空间关联效应，本研究从多维度构建空间权重矩阵，如表 1 所示。

表1 空间权重矩阵及计算方法

2.2.2 空间计量模型

通过空间自相关对中国沿海省份的海洋技术创新效率是否存在显著的空间相关性分析后，可以使用空间计量模型对海洋技术创新与海洋经济发展之间的关系进行研究。目前主要有空间滞后模型、空间误差模型和空间杜宾模型3 种模型［21］。

（1）空间滞后模型。模型的形式如下：

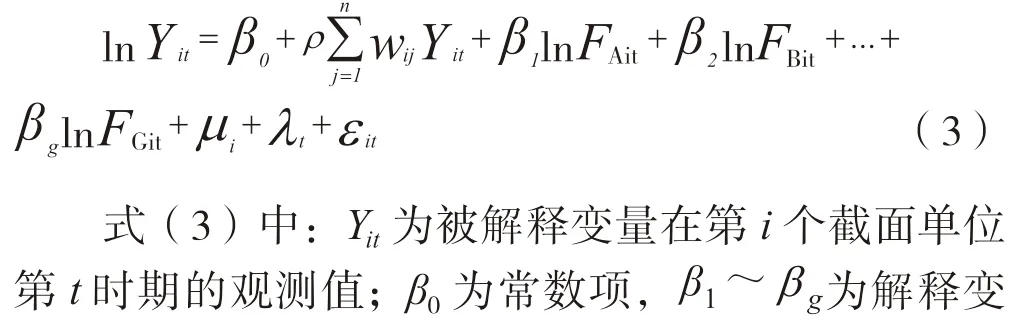
式（5）中，γ为k维列向量，表示空间滞后解释变量的系数［23］。

2.3 指标选取

2.3.1 三阶段DEA 指标选取

使用三阶段DEA 方法进行效率测评时，需要选择合理的投入与产出指标。科技创新效率测评的投入指标选取，大多需要考虑到人力和资本这两个最重要的方面［24］，产出指标则应该充分体现海洋科技成果，因此，结合孙才志等［25］、谢子远等［26］的研究，根据数据可得性和指标非共线的原则，以海洋科研机构活动人员数表示人力、海洋科研机构活动人员中硕士及以上学历比重表示人才、海洋科研机构科研经费表示资金，从这3 个维度构建投入变量；产出方面，选取最能代表科技产出的海洋科研机构科技课题数和海洋科研机构科技专利授权数两项指标。

关于三阶段DEA 中第二阶段需要考虑的环境变量，Furman 等［27］认为制度、政策也会影响到科技产出绩效，因此，在余泳泽等［28］、赵增耀等［29］研究的基础上，选取政府支持力度、海洋高等教育水平、对外开放水平这3 个对本研究中海洋科技创新两产出影响较大的环境变量，分别用海洋科研机构科研经费中政府投资占比、海洋专业硕博士在校人数、进出口总额占GDP 比重来表示。

2.3.2 空间计量指标选取

关于被解释变量海洋经济发展水平的衡量指标，相关研究很多，指标体系也多种多样，结合殷克东等［30］、张继良等［31］的研究，选取海洋从业人员人均GDP 以及海洋经济增长速度这两项既能表示海洋经济发展现状，又能体现海洋经济发展潜力的指标来表示研究对象的海洋经济发展水平。

对于控制变量的选取，结合常玉苗［32］、刘桂春等［33］、王泽宇等［34］的研究，选取资金投入、海洋资源水平、海洋产业结构、地区经济水平、海洋产学研、市场化水平、海洋高等教育水平等7 个环境变量，以及核心解释变量海洋科技创新效率，一同解释海洋经济发展水平，分别以人均固定资产投资增速、渔业总产量、海洋经济的二三产业占比、人均GDP、私营单位就业人员占总人口比重、海洋科技项目中科技服务比重、海洋专业高校在校学生数占海洋从业人口比重表示。

2.4 数据来源

本研究的原始数据主要出自2009—2018 年的《中国海洋统计年鉴》《中国统计年鉴》，以及中国沿海11 个省份（以下简称“样本区域”）的统计年鉴和统计公报。

3 海洋科技创新效率测度

3.1 第一阶段传统效率测评结果

借助软件DEAP2.1 软件，选取BCC 模型对样本区域2008—2017 年的海洋科技创新效率进行分析，结果如表2 所示。海洋科技创新效率一直维持在技术有效前沿面的仅有江苏一个省份；上海、广东两省市的综合效率值基本也都达到最优值；辽宁、山东两省在2015 年前效率都比较高，达到效率有效，但此后效率值便出现不同程度的下降，尤其是辽宁，在2016 年和2017 年下降幅度十分明显；广西、海南两省份的效率值在这10 年间的波动极大，且无明显趋势和规律；其他省份效率值的变化幅度则相对较小。整体而言，第一阶段样本区域的海洋科技创新效率平均值较高，但变化幅度也偏大，走势和规律也不明朗。

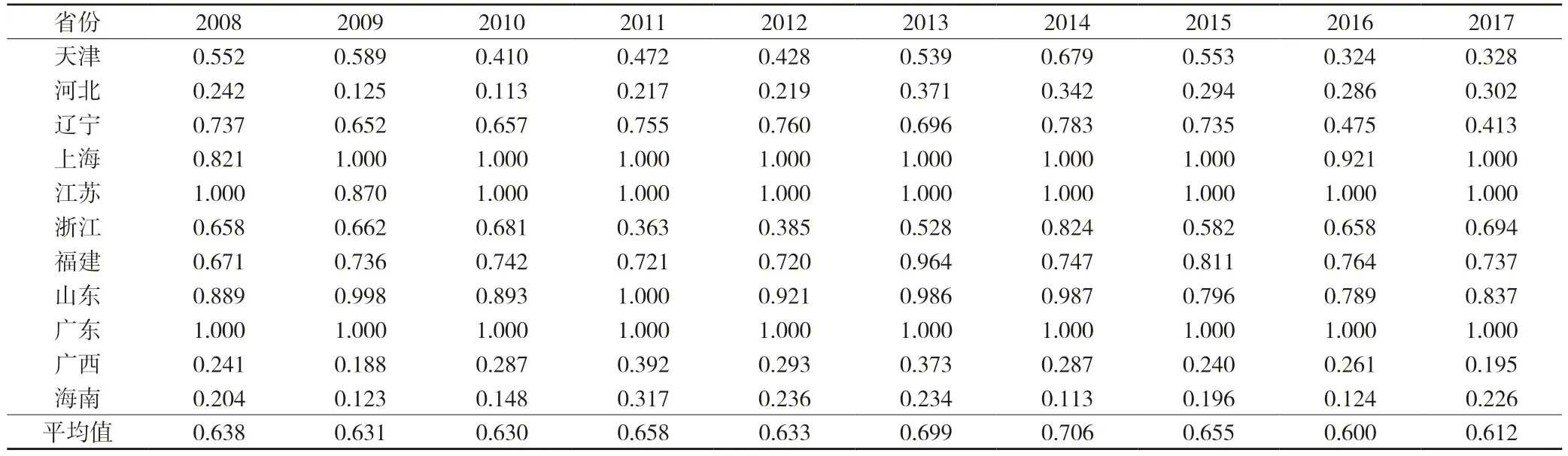
表2 2008—2017 年样本区域第一阶段海洋科技创新DEA 效率值

3.2 第三阶段效率测评结果

在第一阶段DEA 计算结果的基础上，得出投入指标海洋科研机构活动人员数、海洋科研机构活动人员中硕士及以上学历比重和海洋科研机构科研经费的松弛量，将其作为被解释变量，政府支持力度、海洋高等教育水平、对外开放水平等环境因素视为解释变量，利用Frontier4.1 软件进行最大似然估计。在各指标T 值和LR 单边似然比检验都通过的情况下，将变量的值代入公式，即可剔除环境变量和随机干扰的影响，从而使得样本区域的3 个投入指标都能处在相同的外部环境和随机因素之下。调整后，结合原来的两产出指标，再次使用BCC 模型对样本区域海洋科技创新效率值进行测算，结果如表3 所示。2008—2017 年，广东省的海洋科技创新效率一直处在最佳状态，上海、山东省和江苏3 省市也处在较优的状态，接近DEA 有效；与之相对的，河北、广西和海南3 省份的效率值都比较低，一直处在全样本区域末端水平。

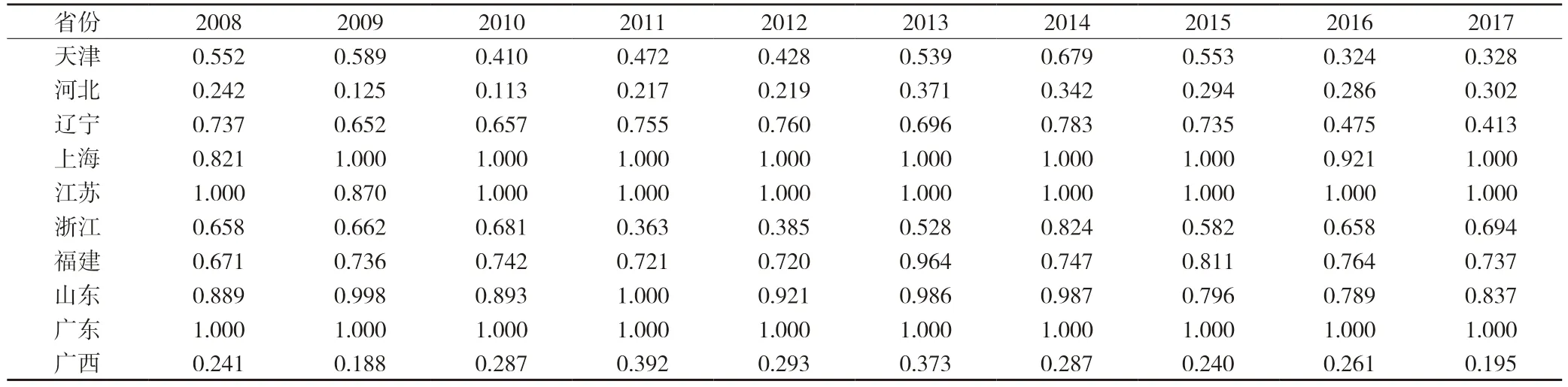
表3 2008—2017 年样本区域第三阶段海洋科技创新DEA 效率值

表3 （续）

从效率构成来看，如图1 所示，我国海洋科技创新纯技术效率很高，都在0.9 以上，达到了最佳值或是接近最佳值，彼此之间差距不大；而规模效率则相对较低，在很大程度上制约了海洋科技创新综合效率的提高。和第一阶段相比，第三阶段的测算结果存在明显差异。总体上，全样本区域的海洋科技创新效率在第三阶段的平均效率值低于第一阶段，但相对于第一阶段在2015 年后出现大幅度下降，波动十分剧烈，第三阶段的平均效率表现较为稳定。在时间序列上，表现为2015 年前趋于逐渐上升，2015、2016 年出现下降，2017 年又开始有所改善；具体到各个省份也是如此，剔除了环境及噪声影响的第三阶段在时间上较为平稳，存在明显的变化规律。空间分布上，第三阶段的海洋科技创新效率差异则更大，地区之间的差距较为明显。

图1 样本区域第三阶段海洋科技创新综合效率平均值变化情况

4 海洋科技创新效率空间计量分析

4.1 数据准备

本研究进行空间计量分析采用的各变量数据描述如表4 所示。对于被解释变量海洋经济发展水平，以2008—2017 年海洋从业人员人均GDP 和海洋经济总值增长速度分别进行极大值标准化处理后相加，从而在保证数据准确性的同时体现样本区域的海洋经济水平及历年来的发展变化趋势和势头。

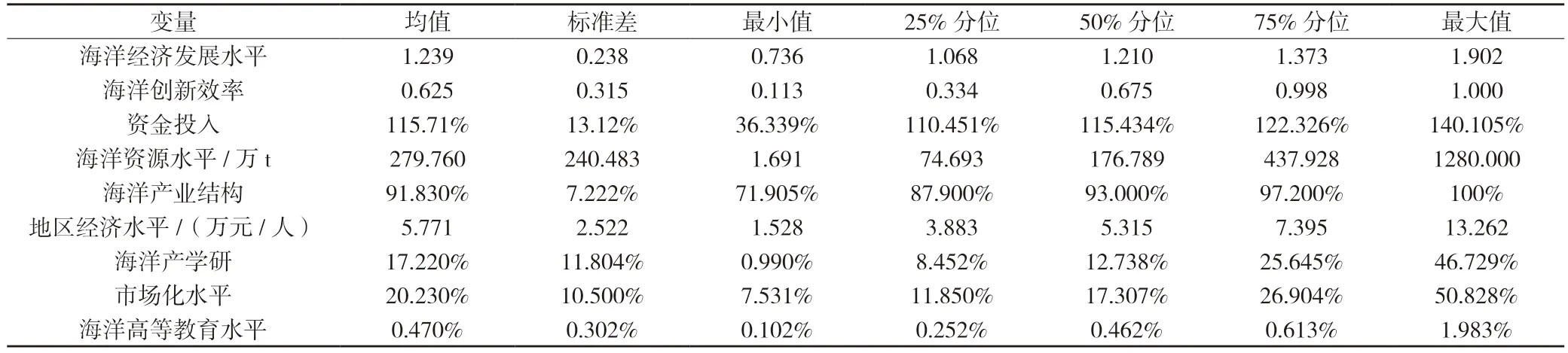
表4 样本区域海洋科技创新影响因素的数据描述

4.2 模型的检验和选择

在进行空间计量分析前，需要对上述4 个不同矩阵上的空间计量模型进行检验和选择。3 个空间计量模型中，空间滞后和空间误差两模型可以通过拉格朗日函数及其稳健形式来比较和筛选；此外，还可以通过LR 检验对空间杜宾模型可否被简化为空间滞后或空间误差模型进行检验。在确定模型后，需要使用Hausman 检验来决定固定效应或随机效应哪个效果更好，以及联合显著性检验比较固定效应、时间固定效应以及双固定效应3 种效应哪个更适合本研究的数据。最终，4 个矩阵上都选取空间杜宾模型，并根据实际检验结果选择了随机效应、个体时间双固定效应，此处不再展开。

4.3 空间溢出效应

基于空间邻接矩阵、交通距离矩阵、经济距离矩阵和嵌套矩阵4 个空间权重矩阵，分别构建被解释变量海洋经济发展水平，核心解释变量海洋科技创新效率及7 个控制变量的回归模型，结果如表5、表6 所示。在除交通距离矩阵外的3 种不同空间权重矩阵背景下，创新效率对样本区域海洋经济发展水平的系数值基本为正且通过了5%显著性概率检验，表明其海洋经济发展和科技创新发展并非呈随机分布状态，而是存在显著的正向空间相关。同时，在空间邻接矩阵、经济距离矩阵和嵌套矩阵模型中，其他大部分解释变量都通过了显著性检验，对海洋经济发展水平的解释能力明显高于交通距离矩阵。考虑到交通距离矩阵的构建仅计算了各省份政府所在地之间的距离，而很多海洋产业、科研机构都分散在各个大小沿海城市，仅依靠政府所在地之间的交通距离来表示区域间的交通联系的确存在很大局限。因此，本研究的这一结果也较为合理。

从回归系数的角度来看，邻接矩阵、经济距离矩阵和嵌套矩阵的核心解释变量海洋科技创新效率均通过了不同程度的显著性检验，效率值分别为0.102、0.051、0.082，显示出科技创新对海洋经济的发展发挥了显著推动作用。此外，资金投入、海洋产业结构和海洋高等教育水平也都显著为正，说明除科技创新外，固定资产投资、海洋经济发展结构和人才储备对海洋经济的发展和推动也有着重要的影响。而海洋资源水平显著为负，由于这个指标是用渔业捕捞总量表示，表明若过于依赖资源开发的第一产业，则对海洋经济的持续健康发展存在一定阻碍作用。经济水平、海洋产学研和市场化水平等几个环境变量大多没有通过显著性检验，对海洋经济发展的影响有限。

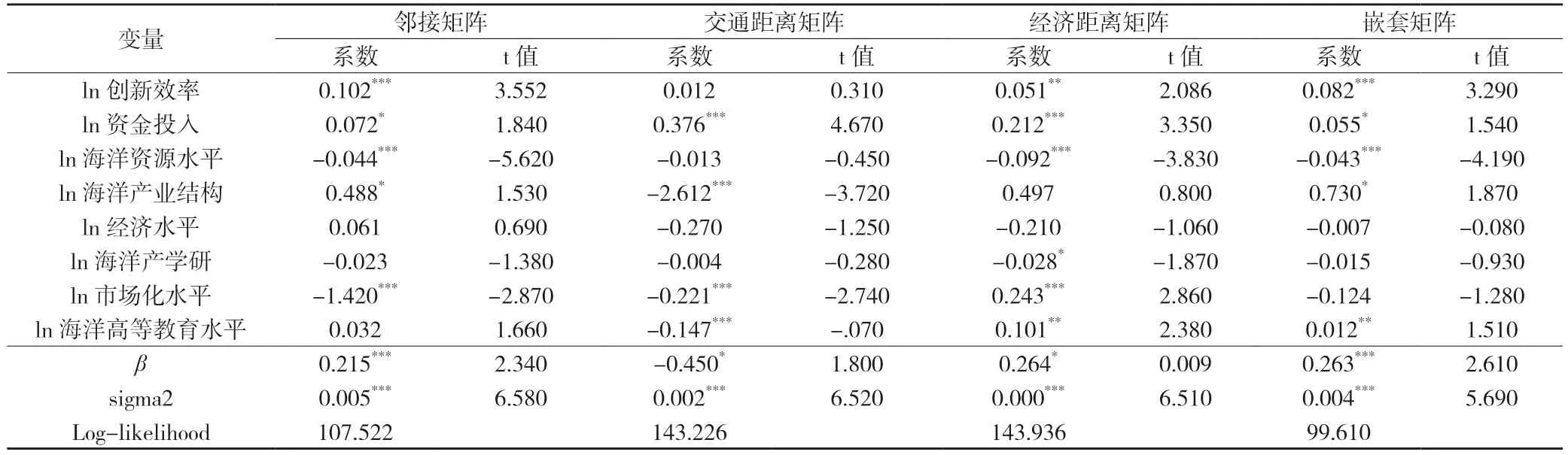
表5 空间杜宾模型中科技创新及其他因素对样本区域海洋经济发展影响的估计结果

直接效应上，创新效率在邻接矩阵、交通距离矩阵和嵌套矩阵上都显著为正，系数值较大且变化幅度小，和其他环境要素相比体现出科技创新对海洋经济稳定的推动作用。间接效应上，创新效率在交通距离矩阵、经济距离矩阵和嵌套矩阵上通过了显著性检验，但系数值仅分别为0.015、0.032和0.011，说明本地区海洋科技创新会影响到与本地区交通、经济有密切联系的其他地区，但影响幅度有限。其他解释变量中，只有海洋高等教育水平在不同的矩阵上的系数都显著为正，即本地区海洋人才的储备能够有效促进邻近地区海洋经济的发展。

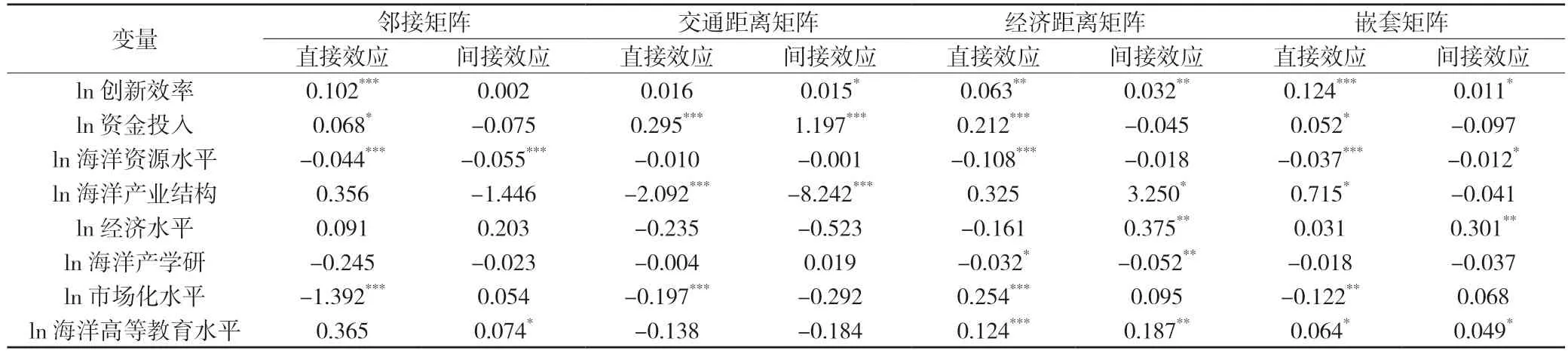
表6 科技创新及其他因素对样本区域海洋经济发展影响的直接效应和间接效应

5 结论和讨论

5.1 结论

（1）基于三投入两产出的效率测度模型，本研究通过三阶段DEA 方法对中国沿海11 个省份2008—2017 年的海洋科技创新效率进行测算，结果表明其中仅有广东省的海洋科技创新效率值在10 年的时间跨度上一直处在最优状态，此外，江苏、上海和山东3 省市也基本达到DEA 有效或接近有效，海洋强省和经济大省在海洋科技创新效率上表现出较为显著的优势；部分经济总量小、发展落后的省份如海南、广西等的效率值则处在11 个省份的末端，最低时仅分别为0.136、0.160，区域间差异较大。时间上，各省份的创新效率值存在波动，2008—2014年呈缓慢上升趋势，2015 和2016 年又出现较大幅度的下降，其中辽宁、天津两省市在2015 年后创新效率的下降是重要的原因，在此期间，辽宁、天津在经济发展上的颓势对其海洋科技创新发展有明显影响，直到2017 年也未出现明显转好的趋势。从规模效率和纯技术效率的角度来看，其中纯技术效率达到DEA 有效的很多，效率值都比较高，海洋科技创新的资源利用效果达到很高的水平；而规模效率明显低于纯技术效率，制约了综合技术效率的提升。在依循各地海洋创新发展的基础上，加大对科技创新规模的投入能够有效改善国内海洋科技创新综合效率值总体不高的现状。

（2）在海洋经济发展的空间效应测度中，核心解释变量创新效率在邻接距离矩阵、经济距离矩阵和嵌套矩阵上都表现为显著推动了本地区海洋经济的增长，虽然未表现出对相邻地区海洋科技创新的显著促进作用，但由于系数值相对较高且稳定，如在空间邻接矩阵上，科技创新效率每提升1%，海洋经济发展水平就提高0.102，因此，可以将科技创新视为海洋经济增长最稳健有效的推动因素。为此，应加强相关方面建设，提升海洋创新效率，从而推动国内海洋经济健康长效发展。与资金、人力、产业结构促进经济增长的传统研究结论相同，本研究中，资金投入、海洋科研机构、海洋高等教育等3个环境解释变量体现出对海洋经济具有显著推动作用，但与以往研究结果不同的是，海洋资源水平对海洋经济的直接效应和间接效应都显著为负，不利于本地区以及相邻省地区海洋经济水平的提升。究其原因，可能是因为过于依赖资源阻碍了产业结构的升级，进而影响到海洋经济水平。

（3）在邻近矩阵、交通距离矩阵、经济距离矩阵和嵌套矩阵4 个矩阵中，除交通距离矩阵因仅考虑政府所在地距离而存在设计缺陷，邻近矩阵、经济距离矩阵和嵌套矩阵上的解释变量都体现出对海洋经济发展水平的较好解释能力，说明国内海洋经济及其发展要素存在着地理空间、经济空间上的相互联系。具体来看，邻接权重矩阵的解释能力优于经济距离矩阵，说明海洋经济在地理距离上的相互影响要大于经济距离，在经济距离上的相互交流还有进一步提升的空间；各省份在海洋经济及其创新发展上，除了应和与其地理距离相邻的地区进行沟通，还应该跟上本地区经济发展的脚步，加强与在经济空间上紧密联系地区之间的海洋生产和技术相互交流，进而相互促进，共同提升中国海洋经济发展质量。

5.2 讨论

海洋科技创新是一个复杂的综合性系统，对海洋科技创新效率值的测评也应该从多指标、多角度去考虑，才能保证效率值的准确性，但限于数据的获取，本研究仅从11 省份的海洋科研机构出发，挑选最有代表性的两产出三投入指标，并将其DEA 分析结果视为当地海洋科技效率值，结果并不能完全代表各地的海洋科技创新发展状况，存在一定的局限性。同时，在本研究的空间计量分析过程中，交通距离矩阵上存在着部分指标显著性不明显、回归系数值偏低等情况，毫无疑问，区域之间的相互联系在很大程度上取决于交通便捷程度，但仅考虑政府所在地之间公路、铁路距离的交通距离矩阵存在很大的局限性，并不完全适合省际层面的空间关系分析。此外，还存在着构建动态化空间权重矩阵从而对不断变化的空间关联进行描述等诸多研究视角，都能成为学者们后续研究海洋科技创新效率中可以注意的方向。