我国城市创新规模的分布及结构特征——齐夫定律视角

蒋明华

（东莞理工学院城市学院，广东东莞 523419）

1 问题的提出

创新推动城市发展在客观上可分为若干个阶段，如以创新驱动力来源划分可分为要素驱动阶段、制度驱动阶段和经济社会全面驱动阶段［1］。研究城市创新发展的阶段特征，把握其规律，是我国新型城镇化建设的本质要求。目前，我国的城市发展已经进入到了以制度安排促进资源流动的城镇化发展新阶段［2］，在新时期思考新的城市发展战略时，适时地总结前一阶段中城市创新发展的成绩和经验，找准下一阶段以何种规模的城市为政策着力点显得尤为必要。

累积的研发经费投入、人力资本投资、促进创新的各项政策和创新基础设施是影响城市创新能力的决定性因素，而这些因素共同作用的结果就体现在城市的创新规模［3-4］。根据《中国科技统计年鉴》，以我国各省份专利授权数量来衡量其创新规模，一个省份的专利授权数占我国专利授权总量的比例，若达到十分之几，则该省份为创新规模发达地区；若为百分之几，则为创新规模发展中地区；若低于百分之一，则为创新规模欠发达地区。那么，在1995 年，我国上述3 类地区的数量分别为1、23和10 个，其专利授权数量分别是4 611、35 421 和1 849 件；而在2018 年，上述3 类地区的数量分别为3、15 和16 个，专利授权数量分别是1 069 699、1 095 169 和170 543 件。对比这两年的数据可以发现，从3 类地区的数量所形成的结构来看，底部规模在扩大，结构形态从1995 年的橄榄形演变为2018年的金字塔形；另外，1995 年和2018 年发达地区的专利授权数量占我国专利授权总量的比例分别为11.0%和45.8%，这说明在创新规模上，顶层城市的影响越来越大。而以科技人员来衡量创新规模，也能得到同样的结论。很明显，省级区域创新规模的结构具有向金字塔结构演化的趋势，并且顶层城市的影响日益增大。我们感兴趣的是，如果用城市替代省份作为考察对象，在研究对象更加细化的情况下，城市创新规模的分布是否仍然呈现类似的结构特征呢？是否也有类似的发展趋势呢？顶层城市的影响又如何呢？

如前所述，本研究感兴趣的话题包括以下几个方面：第一，我国城市创新规模是否具有某些稳定的分布和结构特征；第二，我国城市创新规模的分布和结构是否具有某种演化趋势。对于这两个问题，本研究将采用定量分析的方法比较我国城市不同时期的创新规模分布，从中总结城市创新规模的分布和结构特征，并进一步分析其演化规律。此外，本研究还将讨论创新规模顶层城市是否存在及其影响状况。

2 文献综述与研究假设

2.1 城市创新规模的分布特征

新经济地理学认为城市并不是孤立存在的，它们之间总是以物资流通、人口流动和信息交换的方式发生密切联系，从而形成一个互相依存且分工各异的城市体系。在这一城市体系中，各个城市的大小不一、功能不同，地域分布也不均匀，因此，不同的城市体系一般都具有独特的分布特征［5］。认清城市体系的分布特征，掌握其演化机制和规律，直接关系到城市竞争力建设的政策制定和组织实施。由于西方国家的市场化程度较高，其城镇化已处于较发达阶段，因此西方发达国家的城市规模分布具有较高的稳定性［6］。正是这样，西方学者对城市规模分布的研究较早、成果也较丰富，其中一项重要成果就是对齐夫定律（Zipf`s law）的研究。齐夫定律也称“位序-规模定律（rank-scale law）”，是指在城市数量较多的情况下，位序与规模成反比关系，位序越靠前的城市其规模越大［7］。近年来，中外学者在齐夫定律的研究上所取得的共识是，位序排名在前的城市其规模分布服从齐夫定律［8］，即上尾（upper tail）城市的位序与规模成反比，而对于下尾（lower tail）城市的分布规律仍存在较大的分歧。

随着改革开放的进一步深化，我国城镇化已经进入了新的阶段，有了新的内涵，创新已经成为驱动城市发展的主要动力［9］。随着经费、人员、政策和基础设施等创新资源的持续投入，城市形成了一定的创新规模。由于信息网络构建能力、专业化程度、文化多元性、交易的便利程度等诸多方面存在差异，创新规模较大的城市拥有更强的创新资源集聚能力和创新成果扩散能力，对其他城市的影响更大。因此，从创新规模的角度观察，在新的城市体系中城市的分布不一定均匀，位序越靠前的城市其创新规模越大。基于此，本研究提出以下假设：

H1：我国城市创新规模分布符合齐夫定律。就城市创新规模来说，其位序与其规模呈反比例关系，位序越靠前，其创新规模越大。

2.2 城市创新规模分布的演变

中外研究已经证明，城市自由生长是满足齐夫定律分布的重要前提［10-11］，政府的外力干预会改变齐夫定律的分布特征［12-13］。在我国，政府对城市的生长具有重要影响，进而也影响了城市的规模分布。城市生长理论认为，城市的演化主要有两种模式：自上而下的政府指导模式和自下而上的市场竞争模式［14］。其中，在市场竞争模式中，城市生长近似于自组织过程，在这个过程中镇街和小城市借助于自身的优势，不断集聚资源而成长为具有一定规模的城市。20 世纪90 年代以来，由于市场经济体制改革，我国小城镇和中小城市发展主要以带有强烈自组织特征的市场竞争发展模式为主。政府指导模式则近似于他组织机制，主要表现为中央政府指导和影响城市体系的生长。进入21 世纪后，为了推进国家治理体系现代化，理顺中央和地方的关系，中央政府更多地是通过区域规划、空间战略和制度供给等战略手段，以特大城市和大城市为战略着力点指导区域发展［15］，如京津冀一体化战略对于北京、天津、唐山等城市的影响、粤港澳大湾区规划对珠三角地区城市的影响等等。可见，在新时期我国城市的生长受中央政府的影响越来越明显，政府政策对于城市规模分布的影响逐渐增大。

在城市创新规模的演化过程中，政府的作用也日益明显。在市场化改革之前，严格的计划经济体制和户籍制度不但限制了创新资源在城乡之间的流动，也弱化了创新资源在城市之间的流动，导致城市创新能力不足、创新规模分布固化。在市场化改革初期，市场经济体制改革和户籍制度改革逐渐突破了城乡二元制结构，为科技人员和科技资本等创新要素的流动创造条件。虽然，政府力量已经打破了城市创新发展的桎梏，但是，各个城市集聚创新资源的能力存在差异，从而导致创新发展的速度开始出现分化。新时期，中央政府加大了对重点区域交通基础设施的投入，进一步推动城市创新规模的演化，并通过行政区划手段调整城市创新规模分布，尤其是中央政府对重点区域实行定向制度供给，如京津冀、长江经济带、粤港澳大湾区等发展规划纲要，使得这些地区的创新规模增速加快。由于我国的先进创新城市大部分分布在这些战略重点区域，因此，在中央政府的影响之下，这些地区的城市创新发展的速度整体上要高于其他地区。基于此，本研究提出以下假设：

H2：我国城市创新规模分布越来越不均匀。不同城市的创新规模并非按照相同的比例生长，而是增速逐渐出现分化，创新规模较大的城市和创新规模较小的城市比较，二者之间的差距越来越大。

2.3 城市创新规模的等级结构

城市等级（hierarchy of cities）的观点最早源于克里斯塔勒（Walter Christaller）和廖什（August Losch）分别提出的中心地理论（central place theory），两位学者以新古典经济学的理论假设为基础，在均匀的理想平原上构建了城市等级模型［16］。而以克鲁格曼（Paul Krugman）［17］为代表的新经济地理学者通过构建“中心-外围”模型（core-peripheral model），进一步阐明了城市等级结构的形成机理。“中心-外围”模型认为，城市形成的过程就是促进人口与生产资料集聚的向心力和排斥这种集聚的离心力相互作用的过程：距离中心城市越近，外部经济、市场规模等效应的作用越突出，市场潜力越大；而距离中心城市越远，运输成本等外部不经济效应越强，市场潜力减弱。这样一来，就形成了一个以中心城市或中心区域为核心的城市等级结构，如我国的“沿海重要港口城市-周边制造业城市-腹地城镇”城市等级结构。另外，特别需要指出的是，在我国，除了由于空间上的联系而形成的城市等级结构之外，行政区划的影响也不容忽视［18］。由于我国城市具有不同的行政级别，而这些不同级别的城市之间具有领导和被领导关系，从而形成了如“省会城市（副省级城市）-地级市-县级市-镇街”这样一种基于行政级别的城市等级结构。

在城市创新发展方面，出于规模经济和战略着力点的考虑，国家战略性创新基础设施和创新载体大多布局在大城市，再加上大城市所具有的行政级别优势和政策优势，这种创新资源的集聚能力就成为影响城市创新生长的向心力；而土地资源稀缺、人力成本高企以及环境约束增强等规模不经济因素，就是城市创新生长的离心力。以上二者相结合，形成了城市创新规模的等级结构。基于此，本研究提出以下假设：

H3：我国城市创新规模具有明显的等级结构特征。具体来说，就是我国城市创新规模呈现如纺锤形或金字塔形这样的结构特征。

2.4 城市创新规模等级结构的演变

“借用规模（borrowed size）”理论认为，靠近大城市周边的小城镇会出现大城市的经济特征，享受大城市集聚经济的好处，又可以避免如城市拥挤、地价高企等大城市的负外部性［19］。同时，Mejiers等［20］也指出，借用规模具有不可逆性，即中小城市可以借用大城市的规模，但大城市不能借用中小城市的规模。通过借用规模，中小城市分流了大城市的人口和资源，而由于借用规模具有不可逆性，与大城市相比较，这些中小城市的发展速度更快，从而导致我国城市体系呈现扁平化趋势。而在现代交通网络和通信网络的推动下，我国城市向多中心的网络化结构方向发展，进一步强化了城市体系扁平化的趋势［21］。

毗邻创新发达城市的中小城市，可以享受发达城市的创新外溢，依托这些发达城市的科技能力而形成以高端制造业为主要特征的产业体系；同时，这些城市也避免了因为有限的土地资源而导致的高成本，进一步吸引了高端制造业资源，也分流了大城市的部分创新资源，导致其创新规模迅速增长。而对于远离大城市的其他中小城镇来说，以高速公路和高速铁路为代表的现代交通网络将这些城镇高效地纳入到了大城市所形成的城市创新体系中，这些中小城镇虽然远离大城市，但同样也可以利用大城市的创新优势。因此，近年来，由于借用规模效应，我国中小城市的创新发展速度较快。同时，以《国家新型城镇化（2014—2020）》为主的国家规划提出了严格控制特大城市人口规模、合理确定大城市人口规模等政策，控制了大城市的发展节奏，同时也减缓了大城市创新发展速度，因此，近年来我国大城市创新发展速度相对放缓。小城镇和中小城市创新发展速度加快，意味着“塔基”部分城市数量增加，而大城市创新发展速度放缓，可能导致“塔尖”部分城市数量不足，从而使我国城市创新规模的等级结构出现扁平化。基于此，本研究提出以下假设：

H4：我国城市创新规模的等级结构呈现扁平化趋势。小城镇和中小城市创新规模生长速度加快，与此同时大城市创新规模生长速度放缓，从而导致我国城市创新规模等级结构呈现扁平化。

3 研究设计

3.1 模型构建

3.1.1 齐夫模型

本研究目的是探讨我国城市创新规模分布的基本特征，即我国城市创新规模是否和人口规模、建成区面积等城市属性一样符合齐夫定律。基于此目的，本研究首先简要介绍三参数齐夫模型，并将两参数和单参数齐夫模型作为其特例。

三参数齐夫模型的原型可追溯到1982 年，是由Mandelbrot［22］提出来的。经过Chen 等［8］的改进，三参数齐夫模型表达式如式（1）所示：

式（1）中：r（r=1，2，3......）为城市大小的位序；P(r)表示数据集中排在第r位的城市规模，比如当r=1 时，表示数据集中最大城市的规模为P(1)；K是平移指数，表示数据集中最大城市和理论最大城市之间的位序差距，P1-k表示位序为（1-k）的城市的理论规模；q为规模指数，q＜1 表示该模型描述的分布比较均匀，q＞1 表示模型描述的分布不均匀。

另外，当k=0 时，得到两参数齐夫模型，如式（2）所示。其中，P1表示理论最大城市的规模。

而如果当k＞0 且q=1 时，得到一种特殊的两参数齐夫模型，如式（2）*所示：

再进一步假设k=0 且q=1，那么就得到单参数齐夫模型，如式（3）所示：

3.1.2 等级结构模型

本研究另一个重要目的是探索城市创新规模的结构特征，具体来说，就是我国城市创新规模是否呈现明显的纺锤形或金字塔形。为此目的，本研究引入了等级结构模型。

假设某个城市体系里的所有城市可以分为m（m=1，2 ）个等级，fm表示第m级城市的数量，其中，f1是指理论上顶层城市数量，δ为数量等级参数。给定数量等级参数，如δ=2，则会得到一个关于城市数量的等比序列，如1、2、4、...、2m-1；然后，对照数据集，可以计算出每一层级城市规模的上下限和平均值，从而得到一个基于数量的等级结构模型，如式（4）所示：

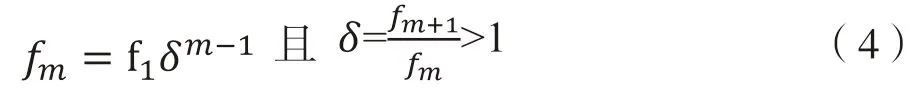
必须注意到，这个模型的底层通常都是错误的。这是因为，在理论上，如果我们设定共有m个层级，那么就不会存在第m+1 级，从而也就不存在fm+1，从而导致对δ的计算出现错误；在实践上，无论采用什么样的方法来建模，都会有不完整的数据集或成长不足的小城镇，从而导致模型出现错误。因此，本研究不考虑这个模型的底层。另外，有研究将不完整的底层称为“跛鸭层”（lame-duck class）［8］，在图形上“跛鸭层”表现为异常值。

3.2 模型验证

3.2.1 数据筛选

本研究基于Chen［23］的经验方法对城市数据进行筛选。首先将城市创新规模及其相应的位序数据都取对数，然后进行线性回归，应用普通最小二乘法（OLS）估计得到残差，如果在0.05 显著水平上标准化残差的绝对值大于2，则将相关数据点视为离群值。

3.2.3 齐夫模型的估计

用筛选之后的数据估计齐夫模型。将OLS 估计应用于三参数齐夫模型的对数版本，如式（5）所示，并逐步增加平移指数k，直到拟合优度R2最大。根据k 值，得到一个描述规模分布的齐夫模型。当R2最优时，如果k=0 且q=1，则估计出单参数齐夫模型，即式（3）；如果k=0 且q≠1，或者k＞0 且q=1，则估计出两参数齐夫模型，即式（2）和式（2）*；如果k＞0 且q≠1，则估计出三参数齐夫模型，即式（1）。

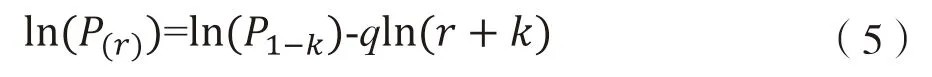
3.2.4 等级结构模型估计

本研究拟构建城市创新规模的数量等级结构模型并对其进行估计。假设数量等级参数那么不同等级的城市数量将是一个几何序列，如1，2，4，...，2m-1，对照样本数据就可以计算出每个级别城市的平均规模，从而导出城市体系的数量等级结构，再采用OLS 检验数据集的拟合程度。

3.3 数据来源

本研究选用《中国城市统计年鉴》中城市（市辖区）的科学支出来衡量城市创新规模。该指标的优势在于：第一，城市的科学支出其实包含了城市所拥有的科研机构、科技人员和重大项目等内容，而这些指标正是城市创新规模的主要体现，因此，相比较研发人员、专利数量等指标，用科学支出衡量城市的创新规模更加合理；第二，城市的科学支出是政府财政支出的一部分，比较起企业研发费用来说，数据统计更全面、更准确；第三，城市的专利数量和研发人员并不一定与城市创新规模成正比，因此，用城市科学支出来衡量其创新规模使得研究结果更加具有说服力。

唐为［21］、Chen［23］和Hackmann 等［24］的研究证明，如果城市样本数据较多，就会由于存在大量发育不足的小城镇而导致“跛鸭层”里城市数量较多，而在建模时“跛鸭层”是作为异常值来处理的，因此，过多的样本数量并无太大意义。为避免以上问题，本研究选择1995—2018 年《中国城市统计年鉴》中城市（市辖区）科学支出的前100 位城市作为研究样本。

4 实证研究

4.1 数据处理

首先用图形展示数据集的大致情况。考虑到相对于位序来说，用科学支出表示的城市创新规模的数据一般较大，不利于直接构建“位序-规模”散点图，本研究采用“位序-科学支出”双对数的散点图来展示1995—2018 年中每一年的数据情况。其中，x轴表示位序的对数，y轴表示科学支出的对数。我国城市创新规模的分布大致呈现以下几个特征：

第一，从1995 年到2018 年，理论创新规模首位城市的创新规模逐年增大。图1 中，“位序-科学支出”双对数回归线在纵轴上的截距表示的是理论上首位城市的创新规模，该截距从1995 年到2018年明显逐年增大，表明在理论上我国创新规模首位城市的规模逐年增大。

第二，从1995 年到2018 年，城市创新规模的分布趋于不均匀。从图1 显示的4 个年份情况可以看出，“位序-科学支出”双对数回归线越来越平，这说明随着规模的下降，城市位序下降幅度更大，从而可以推断随着时间的推移，我国城市创新规模的分布趋于不均匀，即创新规模指数q值有可能逐年变大。

第三，我国城市创新规模有可能呈现等级结构。从图1 可以看出，历年来我国城市创新规模的分布呈现上尾稀疏、下尾密集且越往下越密集的状态，这正是等级结构的分布特征，说明我国城市创新规模有可能具有等级结构的特征。

第四，在创新规模上，顶层城市的差异比较大。图1 显示，我国城市创新规模的分布呈现上尾数据差异较明显且下尾数据拟合较好状态，这说明在创新规模方面顶层城市的变异较大，因此顶层城市的变化可能是影响我城市创新规模分布特征的主要因素。

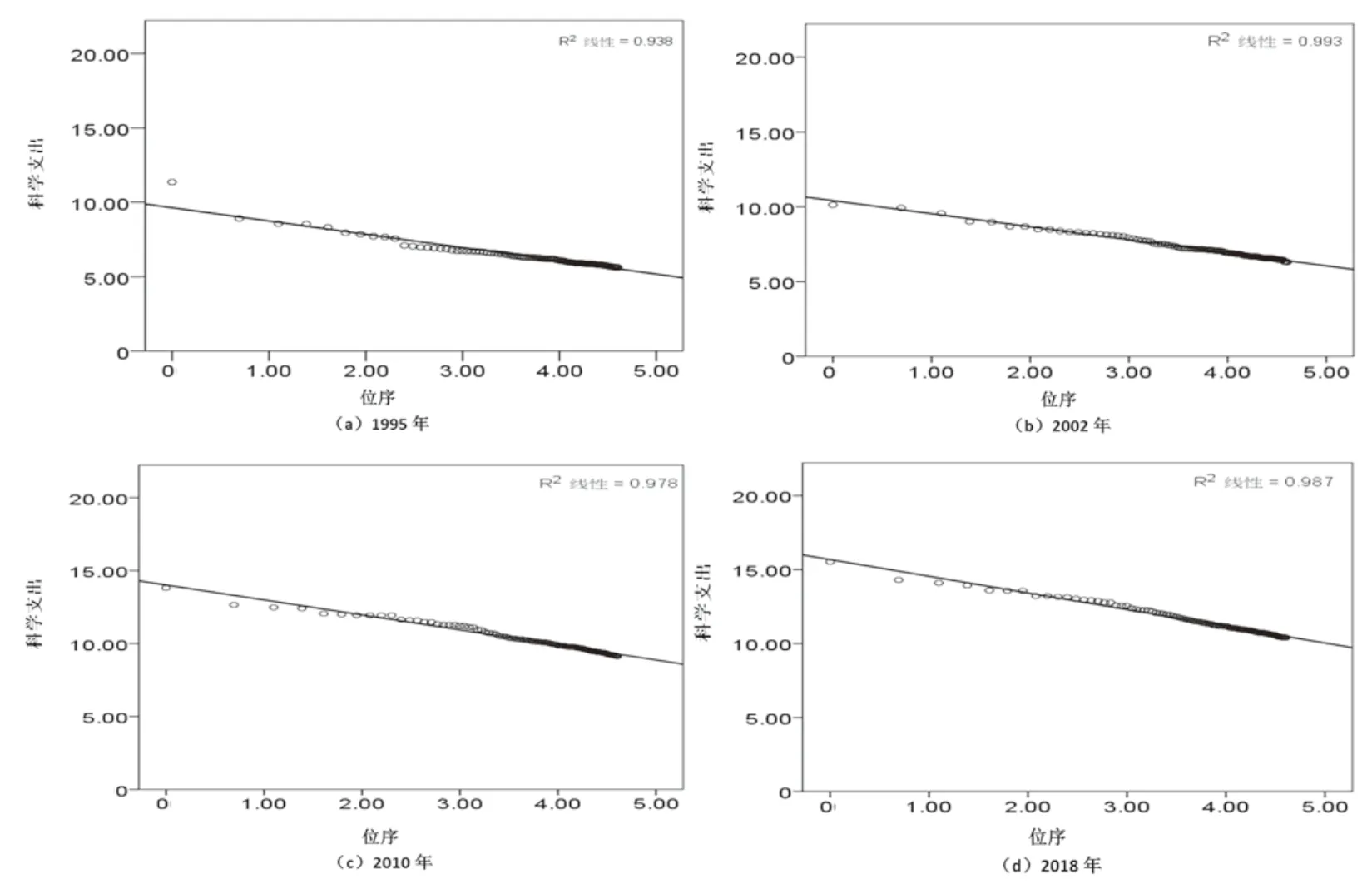
图1 样本城市创新规模的“位序-科学支出”双对数散点图

另外，从图1（a）中可以看出，样本中明显存在离群值，因此有必要应用统计方法筛选数据。本研究对“位序-科学支出”双对数进行回归分析，得到标准化残差值，在0.05 显著水平上将残差绝对值大于2 的样本视为离群值［8］，在齐夫模型估计中不再考虑。样本筛选之后的有效样本容量n如表1所示。

4.2 城市创新规模的分布及其演化

按照模型式（5）对1995—2018 年的有效样本进行回归，结果如表1 所示，样本城市创新规模的分布情况总体上可以分为两阶段。1995—2005 年是第一阶段，这一阶段的回归结果显示平移指数k=0且规模指数q≠1，说明样本对两参数的齐夫模型拟合较好。其中有3 个例外：其一是2000 年，虽然k=1 时的拟合效果最好，但是由于规模指数q为0.998，接近于1，因此不能排除其符合特殊的两参数齐夫模型；另外两个例外分别是2001 年和2005年，同样也不能排除其符合特殊的两参数齐夫模型。2006—2018 年是第二阶段，这一阶段的回归结果显示平移指数k≠0 且规模指数q≠1，说明这一阶段的样本对三参数的齐夫模型拟合较好。长期来看，虽然存在阶段性的变异，但1995—2018 年的样本数据总体上对齐夫模型拟合较好，即，我国城市创新规模分布符合齐夫定律。因此，研究假设H1得到验证。

表1 样本城市创新规模的“位序-科学支出”双对数回归结果

图2 展示了1995—2018 年样本城市创新规模分布的规模指数演变情况，大致上可以分成3 个阶段。其中：1995—1999 年是第一阶段，在此阶段，规模指数在q＜1 的水平上波动上升，q＜1 说明城市创新规模的分布比较均匀，指数波动上升说明城市创新规模具有向不均匀分布发展的趋势；2000—2006 年是第二阶段，此时，规模指数在q=1 附近上下波动，说明城市创新规模的分布比较稳定；2001—2018 年是第三阶段，这一时期，规模指数波动上升且规模指数q＞1，q＞1 说明城市创新规模已经成不均匀分布，指数波动上升说明这种不均匀分布有加剧趋势。总体上看，1995—2018 年规模指数q呈上升趋势且后期大于1，这说明样本城市创新规模从均匀分布向不均匀分布演变，并且这种不均匀分布仍有加剧趋势，即，创新规模较大的城市和创新规模较小的城市比较，差距越来越大。综上所述，本研究假设H2得到验证。

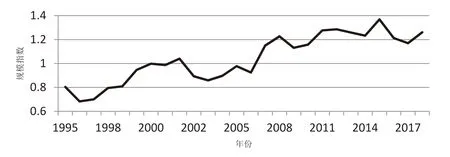
图2 样本城市创新规模指数变化趋势

4.3 城市创新规模的等级结构及其演化

利用上述数量等级结构模型即式（4）考察样本城市创新规模的等级结构。首先，选择数量等级参数。由于每一年的有效样本容量不大于100，而如果选择的数量等级参数较大，则有可能使所构造的等级结构层级数过小且“跛鸭层”城市数量较多，从而无法考察其结构特征。例如，当δ=3 时，构建的等级结构最多为5 层且包括“跛鸭层”，每一层的城市数量分别为1、3、9、27 和60 个，最后一层是“跛鸭层”，这样就导致进入回归的样本数较少，自变量变异程度较小，从而可能导致错误的研究结论。因此，本研究选择的数量等级参数δ=2。然后，根据前文中各年份的平移指数结果，计算数量等级结构中每一层级的城市数量，对照数据集得出每一层级城市创新规模平均值，从而得到一个基于数量的等级结构模型。最后，采用双对数回归模型验证等级结构的拟合优度。从表2 和表3 可以得出以下结论：

首先，1995—2018 年样本城市创新规模呈现明显的等级结构。当数量等级参数δ=2 时，根据平移指数构建的等级结构模型的数据拟合优度较好，且在0.05 水平上显著，说明城市创新规模具有等级结构特征。进一步观察表2 可以发现，样本城市创新规模的等级结构可以分为3 类：第一类是包含首位城市的完整金字塔形（以下简称“Ⅰ”），如1995年，由于平移指数为0，说明存在首位城市，等级结构共有7 层，每一层的城市数量分别为1、2、4、8、16、32 和36 个，其中第7 层的36 个城市构成了“跛鸭层”；第二类是首位城市缺失的扁平形（以下简称“Ⅱ”），如2001 年，平移指数为1，说明第一层（也就是首位城市）缺失，等级结构中实际只有6 层，每一层的城市数量分别为0、2、4、8、16、32 和35 个，其中第7 层为“跛鸭层”；第三类是顶层城市缺失的扁平形（以下简称“Ⅲ”），如2011 年，平移指数为3，说明第1 层到第3 层的顶层城市都缺失，等级结构中只有4 层，每一层的城市数量分别为0、0、0、8、16、32 和40 个，其中第7 层为“跛鸭层”。综上可知，我国城市创新规模具有明显的等级结构特征，且其等级结构可分为3 种类型。因此，本研究假设H3得以验证。

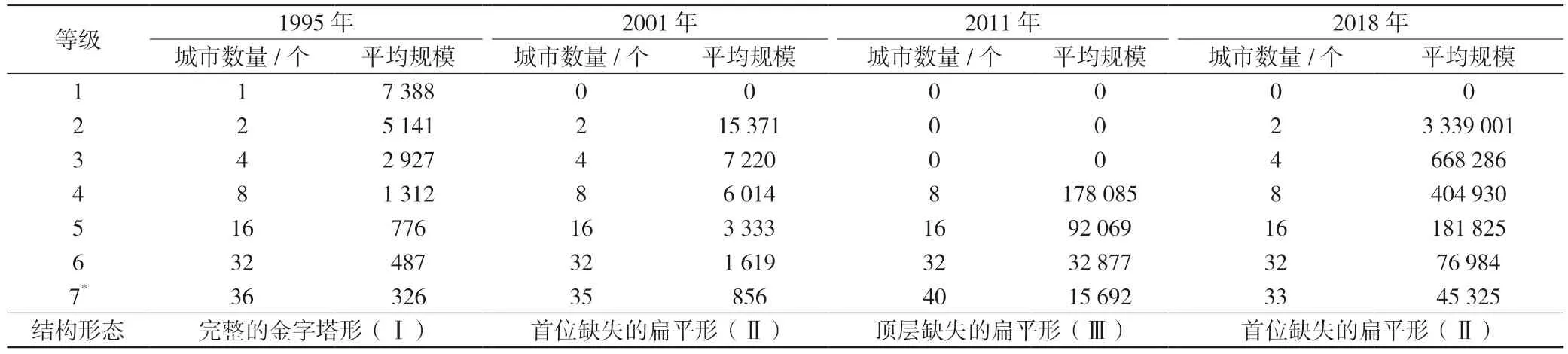
表2 样本城市创新规模等级结构分析

其次，我国城市等级结构具有扁平化趋势。从齐夫模型中的平移指数和等级结构模型中的结构类型这两个方面可以看出：1995—2004 年，大部分年份的平移指数为0，并且等级结构也主要以Ⅰ形为主，而Ⅰ形等级结构中是存在首位城市的，这说明，在这一阶段，样本城市创新规模的等级结构主要以金字塔形为主，未见明显的扁平化；从2005 年开始，平移指数大于1，等级结构主要是Ⅱ形和Ⅲ形，这说明，在这一阶段，样本城市创新规模的等级结构已经显现扁平化趋势；而在2008—2015 年间，等级结构多是Ⅲ形，说明这一扁平化趋势更加明显。综上可知，从2005 年开始，样本城市创新规模等级结构出现了明显的扁平化趋势。因此，本研究假设H4得以验证。

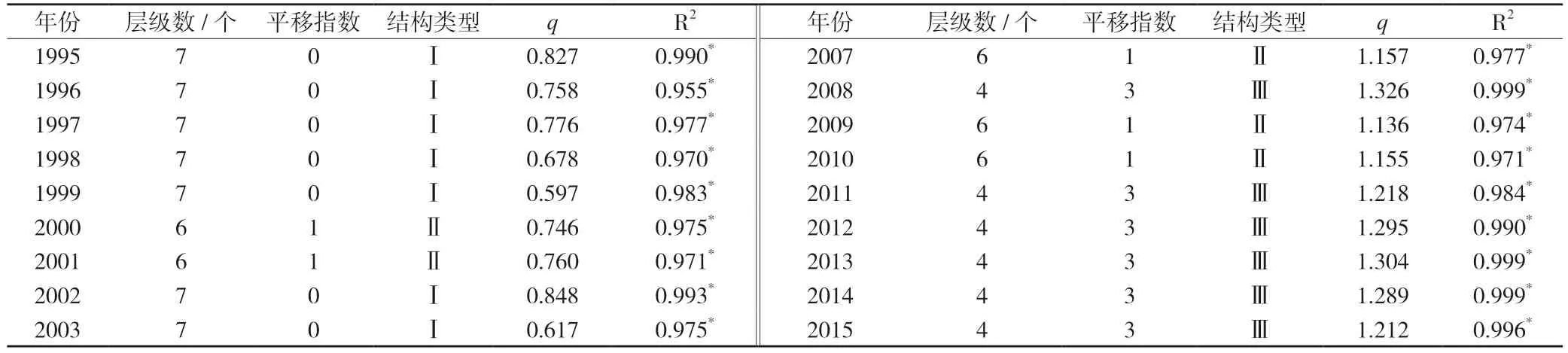
表3 样本城市创新规模等级结构模型双对数回归结果

表3 （续）

最后，等级结构模型可以再一次验证齐夫定律。由等级结构模型所得到的规模指数q的大小与表1中的q值接近，且规模指数q的变化规律与图1 一致。这些结果进一步验证了本研究假设H1和H2。

5 讨论

5.1 齐夫定律的研究重点

近年来，在齐夫定律研究方面产生的分歧越来越明显，一个重要原因就是在齐夫定律的数学表达式方面还未形成共识，其中有不少研究认为严格齐夫模型（单参数齐夫模型即式（3））是齐夫定律唯一表达形式，正由于严格齐夫模型的条件过于严苛，很多关于城市规模是否符合齐夫定律的研究都得出否定的结论。

Gabaix［10］在1999 年曾提出过一个著名的论断，即“城市在发展过程中其规模必然收敛于齐夫定律”。这个论断意味着，即使城市生长规模最终服从众所周知的严格齐夫定律，但也并非是每一个阶段都如此；相反，城市生长的过程可被视为一个进化的过程，其中不同生长阶段可能有不同的齐夫模型表达形式，甚至可能有齐夫定律以外的城市规模分布形式。

城市创新规模分布的三参数齐夫模型具有良好的结构，该模型包括常数项、平移指数和规模指数。其中，常数项表示可能的最大城市创新规模；平移指数表示实际最大城市创新规模与可能的最大城市创新规模之间的差距；规模指数表示每个城市与最大城市在创新规模方面的一致性。当平移指数和规模指数取得特殊值时，三参数齐夫模型可以转化为两参数和单参数齐夫模型。另外，三参数齐夫模型与等级结构模型之间存在联系。这说明，三参数齐夫模型具一般性，可作为齐夫模型的代表；而本研究也证明，三参数齐夫模型对数据拟合效果较好。这也说明，我国正处于城镇化高速发展阶段，城市特征将处在不断的动态调整之中，在这一重要背景下，对于齐夫定律的研究，重点不应放在是否接受或拒绝哪一个齐夫模型上，而是应该关注齐夫定律与城市规模分布的契合程度。

5.2 样本选择对研究结果的影响

李松林等［25］在总结我国城市规模分布的特征时指出，数据的质量是准确研究我国城市规模分布特征的关键，并指出在我国城市规模分布特征的实证研究中，所采用的数据普遍存在以下3 个方面的问题：一是缺乏能够反映城市长期生长的高质量数据；二是未能消除行政区划调整所导致的统计不一致的问题；三是没有剔除虚假城镇化所带来的影响。类似观点也见于其他关于我国城市规模分布特征的研究，如Anderson 等［26］和梁琦等的研究［27］。以上这些研究都主张运用更加精确的数据来测度具体的城市规模分布及其演化，如夜间灯光数据。但同时，以上研究也提到，城市经济学家对城市规模分布研究得出的一个重要共识就是，只有城市规模的上尾部分服从齐夫定律，而下尾部分则不然。例如，李松林等［25］即便是采用了他们认为质量较好的夜间灯光数据，但也是选择高于平均值的城市作为研究样本，也就是说，这些研究者不但仔细挑选哪类数据用于研究，也对这些数据的哪部分能够进入模型做了谨慎的决断。而魏守华等［28］更是讨论了齐夫定律的最优数据截点的问题。

本研究分别对我国1995 年的258 个城市和2018年的285个城市的位序与科学支出的对数进行拟合，结果如图3 所示。从图3 可以看出，数据的上尾部分存在明显的线性关系，而在下尾部分，两个年份的数据发生了明显的折弯下垂。与图1（a）和图1（d）相比较，正是由于下尾部的折弯下垂，使得整个回归直线上翘，从而使得模型不但拟合优度较差，并且也明显偏离事实。而图1 样本是1995—2018 年《中国城市统计年鉴》中前100 名的城市，图3 的样本是其中所有城市（以下简称“全部统计城市”）。这说明，到底哪部分样本进入模型，直接决定着模型拟合的结果。另外，本研究以从事科学技术事业人员的数量代表城市创新规模，也得出了相类似的结论。因此，本研究认为，在研究我国城市规模分布的时候，采用哪类数据作为城市规模的指标当然重要，但是，选择哪部分样本进入模型对于得出正确的研究结论来说显得更加重要。

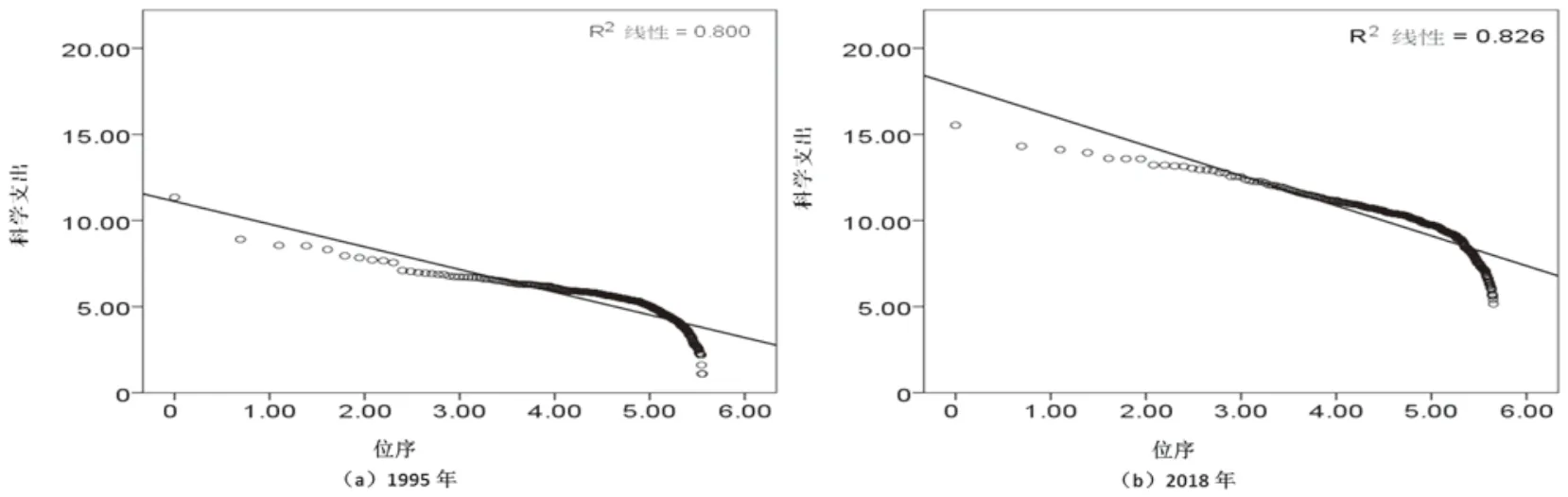
图3 全部统计城市创新规模的“位序-科学支出”双对数散点图

5.3 规模指数变动与等级结构扁平化之间的矛盾

本研究的结果显示，我国城市创新规模分布的规模指数q大于1，说明城市创新规模分布越来越不均匀；而其逐年增大的趋势说明创新规模较大的城市和创新规模较小的城市比较，二者之间的差距越来越大，也就说，城市之间的创新规模生长速度出现了两极化，创新规模较大的城市其生长速度会越来越快，显然，其地位和作用也会越来越突出。这自然地可以得出以下推论：在我国城市创新规模的分布上，会出现“领跑”的若干顶层城市，甚至存在“一骑绝尘”的某个首位城市，用图像表示就是我国城市创新规模呈现金字塔形的等级结构。但是，如表2 和表3 所示，我国城市创新规模却呈现扁平化趋势，甚至是，缺失首位城市或顶层城市。这似乎与前述推论相矛盾。

实际上，这反映的是城市创新规模理论水平与城市实际生长水平之间的差距。前述推论是说，在理论上，我国城市创新规模将呈现存在首位城市或者顶层城市的金字塔结构，但现实的情况是，从2007 年开始，城镇化使更多的镇街和小城市获得了发展，催生出新的塔基层，使得整个等级结构向上新生一层或数层。但是，虽然整个结构向上发展，不过塔基和塔顶城市的发展情况却不同：原来的塔基城市虽然发展速度不如塔顶城市快，但这一发展速度足以让其跃升到更高一层；而原来处于塔顶的城市虽然发展速度较快，但仍不足以支持它们进一步跃升到更尖耸的塔顶，从而导致新的城市创新规模等级结构出现首位或顶层城市缺失，即城市创新规模等级结构呈现扁平化，而反映在图形上就是该阶段的等级结构以Ⅱ形和Ⅲ形为主。因此，可以说，虽然近年来我国创新规模较先进的城市生长速度很快，但总体上我国城市创新规模的等级结构却呈扁平化趋势。而规模指数逐渐增大的趋势与等级结构扁平化之间的矛盾，其实质反映的是城市创新规模理论水平与城市实际生长水平之间的差距。另外，回归模型式（5）中，常数项的数值较数据集中的最大值来说高出很多，这一点也可以从图2 中的纵轴截距看出，也说明了我国城市创新规模的实际最大城市与理论最大城市之间差距较大。

6 结论

本研究利用1995—2018 年《中国城市统计年鉴》的城市数据，定量研究我国城市创新规模的分布特征和结构特征，分析城市创新规模的演变规律，探索其内在机制。研究发现：首先，城市创新规模数据与三参数齐夫模型拟合效果较好，说明我国城市创新规模的分布在总体上符合齐夫定律；第二，虽然存在波动，但我国城市创新规模指数总体上呈上升趋势，说明不同的城市其创新规模出现差异化，且这种差异呈现逐渐扩大的趋势；第三，城市创新规模等级结构拟合情况说明，我国城市创新规模呈现明显的结构特征，不过，不同阶段等级结构类型不一样；第四，齐夫模型平移指数的变化和等级结构的拟合情况说明，虽然我国城市创新规模在不同的阶段呈现不同类型的等级结构，但是长期来看，我国城市创新规模等级结构具有扁平化的趋势。

以上结论对于我国城市创新规模体系乃至其他城市体系的发展具有以下几个方面的启示意义：首先，城市创新规模体系中的齐夫定律分布特征和等级结构特征使城市在发展过程中不仅要注重自身的规划，还要考虑到与其他城市之间的关系，努力形成一个分工合作、协调发展的城市创新体系；其次，政府部门在制定区域空间战略和地区发展规划的时候，必须要注意到城市创新规模分布和等级结构的存在，尊重现有的城市创新规模体系，在加强城市自身创新基础设施建设的同时强化城市对外的功能，促进创新要素的流动，加快科技溢出和扩散，提升城市体系在整体上的创新能力；第三，要客观认识和区分导致“城市病”的原因，不能简单地通过限制城市规模来解决“城市病”，在制定政策时要顺应创新城市的发展规律，突破各种制度性障碍，鼓励资本、技术、知识等创新要素在大城市的集聚，建设区域性创新规模首位城市。