基于禁忌搜索差分进化的组合系统选星算法*

朱 军，许士杰

（安徽大学，安徽 合肥 230601）

0 引言

目前，随着导航定位系统的发展，全球定位卫星的数量空前巨大，包括美国的GPS，俄罗斯的GLONASS，欧洲的伽利略和中国的北斗系统。随着卫星数量（即导航信号源）的增加，准确和实时定位的必要性变得越来越重要。冗余信号可以有效地提高定位精度，但是同时信号处理成本也急剧增加[1-2]。如果接收机使用更多的卫星进行定位，则由于高计算处理量，作为定位系统的关键标准的实时定位将无法实现。因此，需要一种平衡精度和性能的可见卫星选择方法。

卫星选择的标准是可见卫星和用户接收机之间的空间分布的好坏，例如，几何精度因子（Geometric Dilution of Precision，GDOP），由测量误差与输出位置的误差之比定义。较小的GDOP值表示更准确的定位[3]。遍历选星算法（Exhaust Search，ES）从所有可见卫星中遍历所有组合以找到最优卫星组合，但选星耗时较大。因此，研究人员一直致力于GDOP计算和基于几何分布的卫星选择方法的开发，以降低计算成本并实现最小的GDOP[4-6]。研究者利用群体智能优化算法减少GDOP计算，实现快速选星[7-9]。其中，Meng等人对遗传算法（Genetic Algorithm，GA）进行改进，提高了算法选星结果的准确性。尽管遗传算法的性能与卫星几何分布无关，但在实现GA 的计算过程中涉及参数过多，过于依赖参数设计，若设计不当，很难提高选星速度。

与GA不同，差分进化（Differential Evolution，DE）算法在变异操作方面采用差分策略，利用种群个体间的差分来扰动进化方向，避免GA中变异方式的不足，并且需调整参数大大减少。此外，基于禁忌搜索思想，以提高算法速度，提出一种混合的差分进化选星算法。

1 组合系统选星模型

组合系统选星问题可描述为：当可见卫星数目为N时，从中选择N颗卫星参与导航定位。于是，基于群体智能优化算法的思想，解空间为CMN，依据目标函数最小的标准从解空间中寻找最优的目标解。其中，目标优化函数与可见卫星和用户接收机的位置信息有关。

在组合系统中[10]，卫星定位的精度主要与以下两方面因素有关：一是卫星测量误差，测量误差的方差越大，定位误差的方差越大；二是卫星的几何分布。

三维空间定位误差的标准差σp可以表示为GDOP与用户等效距离误差（User Equivalent Range Error，UERE）σUERE的乘积：

从式（1）可以看出GDOP值和UERE决定了定位精度。GDOP可以看作是定位误差对UERE的放大。因此GDOP可以在一定程度上反映卫星组合的定位精度[10]。

GDOP表示从用户接收机指向可见卫星组合的几何形状，更好的几何形状的定位误差较小。在卫星选择中，GDOP的值可作为优化目标，且GDOP的计算可描述为：

式中，G为观测矩阵，由可见卫星与用户接收机的位置矢量组成：

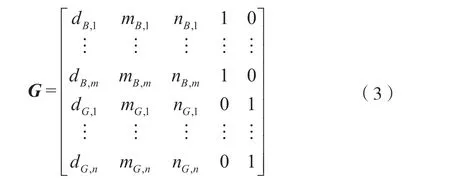
式中，下标B和G分别代表BDS卫星系统和GPS卫星系统；下标1,…,m和1,…,n分别代表可见BDS卫星和GPS卫星的索引；(d,m,n)T是用户接收机指向可见卫星的单位矢量。从式（2）和式（3）可以看出，GDOP仅取决于用户和空间中可见卫星的几何分布。于是，以GDOP作为卫星选择标准，仅考虑几何分布，且GDOP公式作为目标优化函数。

2 组合系统选星算法

基于选星模型，DE算法可以通过有限次迭代从解空间中快速搜索符合条件的最优解。然而在单独使用DE时，无法对已搜寻过的解进行屏蔽，因此，本节讨论了一种具有禁忌搜索机制的差分进化选星算法（Tabu-Search DE，TSDE）。以下各节介绍DE算法的基本概念，并对主要参数和操作进行详细描述，包括对TSDE算法进行修改以解决上述组合系统选星问题。

2.1 差分进化结构

差分进化算法是一种模拟生物进化的随机模型，通过有限次数的迭代过程，将那些能适应生存条件的个体保存下来[11]。

DE主要由初始化种群、变异、交叉及选择四个步骤组成，进化过程可描述如下：

（1）种群初始化。从解空间中随机选择部分解作为目标个体，每个个体由D维向量组成，从而生成初始种群。

（2）变异。在某一代中，从种群中随机选择几个不相同的个体组成差分向量，在变异因子F的缩放下产生变异个体。其中，变异因子F一般取值范围为(0,1)。常用变异策略为：

式中，Vi,g、Xi,g和Xr,g分别表示即将获得的g代中第i个变异个体，g-1代的第i个目标个体和随机目标个体，且各不相同。式（4）是经典差分变异策略。

（3）交叉。在变异后，需要将目标个体与变异个体进行交叉操作生成最终的试验个体。常用交叉策略为二项式交叉，即：

式中，CR为交叉因子，jrand表示{1,2,…,N}中的任意一个整数，保证变异个体至少有一维基因被保存。

（4）选择。试验个体与对应的目标个体一一比较。选择依据为适应度函数（本文中即目标函数GDOP）的值，若试验个体具有更优的目标函数值，则将与之对应的目标个体替换为试验个体；反之，该目标个体保持不变。在本文中，以适应度函数最小为选择标准。

根据相关研究[12]，本文引入禁忌搜索中的“禁忌列表”，避免重复计算GDOP。从式（2）和式（3）中可以看出，矩阵求逆涉及GDOP的计算，这相对耗时。禁忌列表记录了已计算出GDOP值的所有组合。在上述解决方案选择过程中，该算法避免搜索禁忌列表中已经存在的卫星组合。

在下一节，将具有禁忌搜索思想的差分进化引入组合系统的卫星选择问题中。

2.2 TSDE选星算法设计

假设某历元时刻对于用户接收机的可见卫星为M颗，从中选择N颗卫星参与计算，获得尽可能小的GDOP值。执行以下搜索过程即可找到符合条件的目标解。

步骤1：获取可见卫星。根据一定的截止高度角获得可见卫星位置信息，计算该历元时刻的可见卫星数目M。

步骤2：编码。将可见卫星编码为序列S={1,2,…,M}，且每个编码元素对应一颗卫星。

步骤3：初始化种群。N颗卫星为一待选组合，则共有个组合。从中随机选择R个子组合作为种群个体Xi，每个个体具有D=N维基因，生成初始种群P。

步骤4：差分变异。设置变异因子F，采取变异策略式（6），生成变异个体Vi。

步骤5：二项交叉。设置交叉因子CR，通过二项交叉式（7）产生试验个体Ui。

步骤6：禁忌列表。记录初始种群中个体和执行上述步骤后的个体。

步骤7：适应性比较。根据适应度函数，比较试验个体与目标个体的适应度值，保留适应度值更小的个体，并根据比较结果更新最优个体，直到达到最大进化代数，终止进化。

在执行以上算法步骤时，还应注意以下问题：一是因卫星编号序列全为整数，是与可见卫星一一对应的，因此在进化中应保持个体基因为整数；二是基因“越界”问题，在经过变异操作后，可能产生超出界限的基因，该界限应限制为1～M。

3 仿真评估

本文使用卫星仿真平台输出的BDS/GPS组合系统场景下用户接收机及卫星的位置信息，并进行仿真实验[13]。GDOP值的变化随参与导航的可见卫星数量而变化，并随卫星数量的增加而单调下降，但会受到限制，且根据可见卫星数量和能满足基本定位，接收机完好性监测（Receiver Autonomous Integrity Monitoring，RAIM）等条件，本文选择参与计算的卫星为6颗[14-15]。

设置接收机大地坐标为东经117.28°，北纬32.87°，截止高度角为5°，仿真起始时间为2021年2月1日00时00分00秒，时长24小时，时间间隔10 min。在实验中，根据TSDE算法选星步骤设置仿真参数：种群大小R=50，变异因子F=0.5，交叉因子CR=0.5，进化代数T=50。本节将以遍历法和基于GA的选星算法为参考，分析所提选星算法的性能。

基于已设置的截止高度角，一天24 h内可见卫星数目如图1所示。

图1 各历元时刻可见卫星数目分布

从图1可以看出，在历元时刻3时，可见卫星数目为26颗，在采用遍历法选星时，可知需要进行次的GDOP公式的计算，选星耗时为12.974 s，显然不适应组合系统场景。

图2为3种算法的不同的GDOP变化，在一天内，基于TSDE的选星算法与基于GA的选星算法相比，与ES选星算法的GDOP分布更加接近。而且TSDE选星算法的GDOP值均在3以下，相比GA选星算法可以提供更高精度的导航定位服务。

图2 24 h内3种算法的GDOP的变化

为进一步分析TSDE选星算法的稳定性和收敛特性，本文分别在6时和14时两个历元时刻，百次仿真获得TSDE与GA的GDOP均值、标准差和平均收敛代数，仿真结果如表1所示。

表1 TSDE与GA的GDOP均值等参数

从表1中可以看出，TSDE选星算法在6时和14时的GDOP标准差和均值均小于基于GA的选星算法，具有更高的稳定性，且获得最优解的收敛代数更小，具有更快的计算速度。

为充分验证基于TSDE的选星算法的快速寻优能力，在组合系统选星问题中，3种算法的整体性能验证结果如表2所示，其中在该历元时刻，可见卫星数目为23颗。

表2 3种算法的性能比较

从表2可知，相比GA选星算法，基于TSDE的选星结果也未完全达到ES的结果，但更加接近于ES；经统计分析，对比ES算法，基于TSDE和GA的选星算法在GDOP的偏差上分别增大了2.15%和4.85%，在执行时间上分别减少了92.79%和85.73%；但TSDE选星算法相比GA在GDOP值和执行时间上分别减小了2.58%和49.43%。

4 结语

本文提出了一种基于禁忌搜索机制的差分进化的卫星选择算法，并将其与传统的ES算法和基于GA的选星算法进行比较。分析结果表明，相比于GA选星算法，TSDE选星算法的GODP值降低了2.58%，更接近于ES选星结果；选星速度减少49.43%。得益于禁忌搜索机制，TSDE选星算法的快速寻优特性表明在组合系统选星问题中的优异解决能力。本文所提算法优于需要调节过多参数的遗传算法，且为组合系统选星提供解决新方案。