基于钻孔应变地震波记录确定地震面波应变震级
李富珍, 张怀* , 唐磊, 石耀霖
1 中国科学院大学地球与行星科学学院, 计算地球动力学重点实验室, 北京 100049 2 应急管理部国家自然灾害防治研究院, 北京 100085
0 引言
地震震级是表示地震本身大小的重要物理量(陈培善,1982),常用的地震波面波和体波震级描述地震震源辐射地震波能量的强度,可以通过测量地震波波动造成的地动位移的最大振幅值来获得(陈运泰和刘瑞丰,2004;赵瑞等,2017).近震震级ML通过S波最大振幅计算(Richter, 1935),远震面波震级MS由周期20 s左右的面波最大振幅计算(Gutenberg, 1945a),体波震级mb由1 s左右的体波最大振幅计算(Gutenberg, 1945b).各种震级间存在一定的经验关系(Gutenberg and Richter, 1936;刘瑞丰等,2007).除了地震位移记录,也可以利用地震速度计记录的地震波持续时间求地震震级(李慧民等,1992;刘瑞丰等,1996).
地震速度计记录的是地震位移对时间的一阶微分,而钻孔应变计记录的是地震位移对空间的一阶微分.对于入射的平面波,二者有类似之处,原则上也可以尝试用应变记录来测定地震震级.较早部署的钻孔应变仪采样频率为1 Hz到10 Hz不等,对于远震可以利用面波确定震级.目前钻孔应变记录采样率达到每秒100次,也应该能用于确定近震震级.前人研究中已开始涉及利用钻孔应变观测数据测定地震震级的工作,如毕永强等(2013)利用敦化地震台YRY-4型钻孔应变仪记录的应变地震波持续时间测定大震震级,彭华等(2008)及陈启林等(2015)则探索了利用钻孔体应变的地震应变波测定大震震级.
本文根据我国高台、通化、姑咱等共10个台站YRY-4型钻孔应变仪所记录的应变地震波这一应变直接观测资料(采样率10 Hz),对68个不同震级、不同震中距的地震波形记录开展定量研究,计算最大主应变振幅,并用最小二乘法求得应变震级公式,比较应变震级与中国地震台网中心给出的震级的相关关系,探讨应变震级的可行性,并对单台应变震级和台网平均震级的偏差进行统计分析.
1 资料选取
1.1 地震波记录和台网地震目录资料
四分量钻孔应变地震仪通过观测地应力引起的钻孔变形,可以实时获取超宽频带的原位应变和应力变化数据,包括浅地表应力场长期变化、固体潮汐变化、同震阶变和从近震到远震的动态应变和应力变化数据,应变分辨率达到10-10.地震台站的四分量钻孔应变仪可以记录丰富的地震波信息,获取完整的应变地震波形数据(邱泽华等,2020).本文选取10个台站均有清晰记录的地震,并剔除面波可能不发育的深源地震(h>60 km)以及有些台站震中距太近面波不发育的地震;还剔除一些发震时间距离较近、记录在地震图上可能早到的波列对后续地震记录有影响的地震.钻孔应变台站和地震事件的位置见图1.

图1 震中与钻孔应变台站位置图Fig.1 Location of earthquake epicentres and borehole strain stations
从2020年1—3月中国地震台网中心记录的153个地震事件中选取的68个地震,震源深度最深的为40 km,震中距范围1.27°~154.76°,地震震级范围4.0~7.7.其中:4.0~4.9级地震23次,5.0~5.9级地震35次,6.0~6.9级地震8次,7.0~7.7级地震2次.地震的有关参数见表1,来自中国地震台网中心.其震级按《地震震级的规定》发布(刘瑞丰等, 2017).

表1 本文地震的有关参数Table 1 Seismic catalogs in this paper
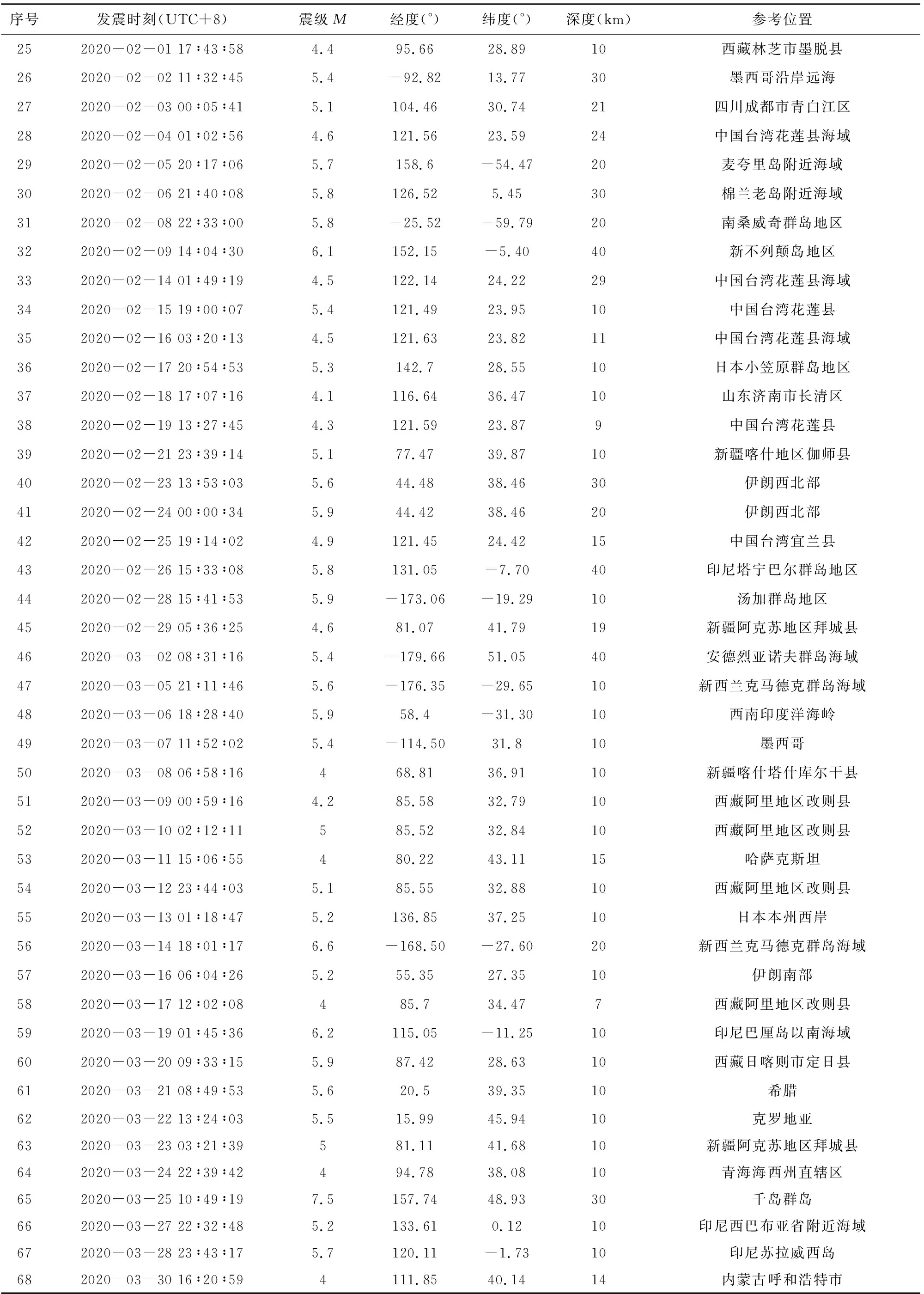
续表1
本文10个钻孔应变台站信息见表2,钻孔应变仪的四路分量方位角以北为0°,顺时针为正,依次间隔45°.
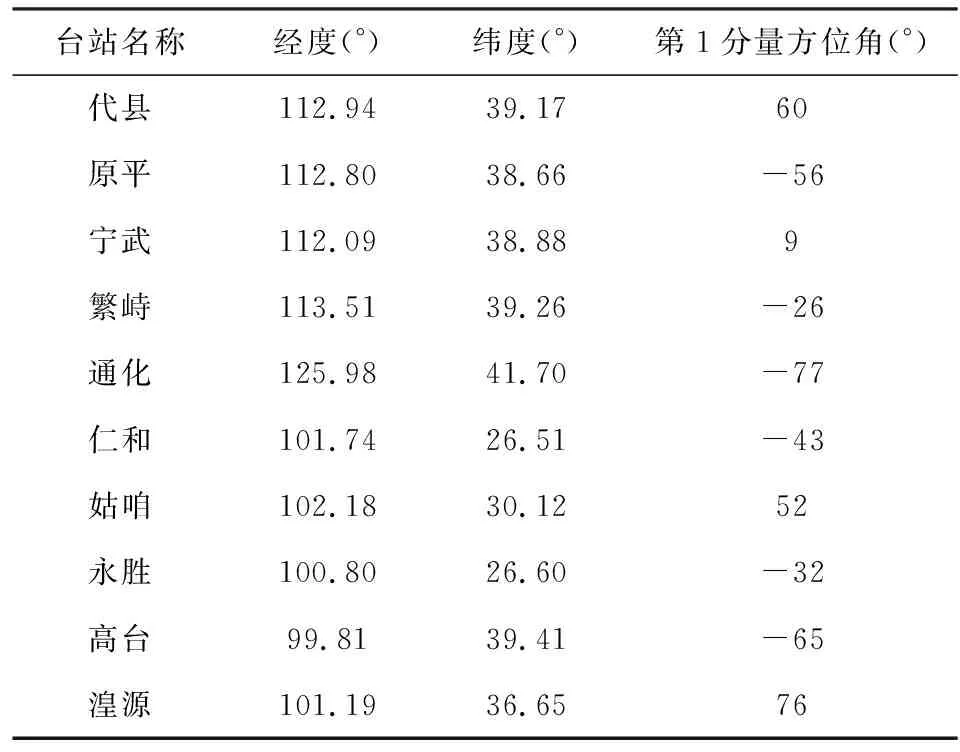
表2 本文10个台站信息Table 2 Information of 10 stations in this paper
1.2 最大主应变振幅的获取
获取钻孔应变观测数据后,首先需要进行数据预处理.由于台站四分量钻孔应变仪不仅能记录到宽频带地震仪器可以记录到的近震、远震地震波形,还能记录更长周期的固体潮汐等信息,为了更好地识别地震事件,首先要对记录的应变地震波数据进行高通滤波(李纲等,2005;白占孝和罗自浩,2011).图2为典型的钻孔应变观测原始记录,图3为高通滤波消除潮汐影响后的地震记录.
四分量钻孔应变仪可以记录四个方向上的应变观测值,使用的资料应满足ΔεI+ΔεIII=ΔεII+ΔεIV的自检条件(石耀霖和范桃园,2000;邱泽华等,2009;池顺良,2019).台站在建台后都做了标定(阚宝祥等,2009),本文采用台站数据提供的标定值.虽然利用潮汐绝对标定值可能有微小变化(石耀霖和范桃园,2000),但变化幅度一般不大.为便于推广使用,原则上使用台站建台给定的标定值.根据石耀霖和范桃园(2000)提供的方法,从钻孔应变仪的四个元件的观测值按最小二乘法可以计算得到水平应变张量的三个分量,并进一步计算得到最大、最小主应变和主方向.本文对10个台站各自记录的68个地震的面波最大主应变振幅进行统计分析.
2 方法与结果
根据中华人民共和国国家标准地震震级的规定(GB17740—2017),测定面波震级的方法是根据面波的最大振幅求地震震级(刘瑞丰等,2017).常用的公式形式为
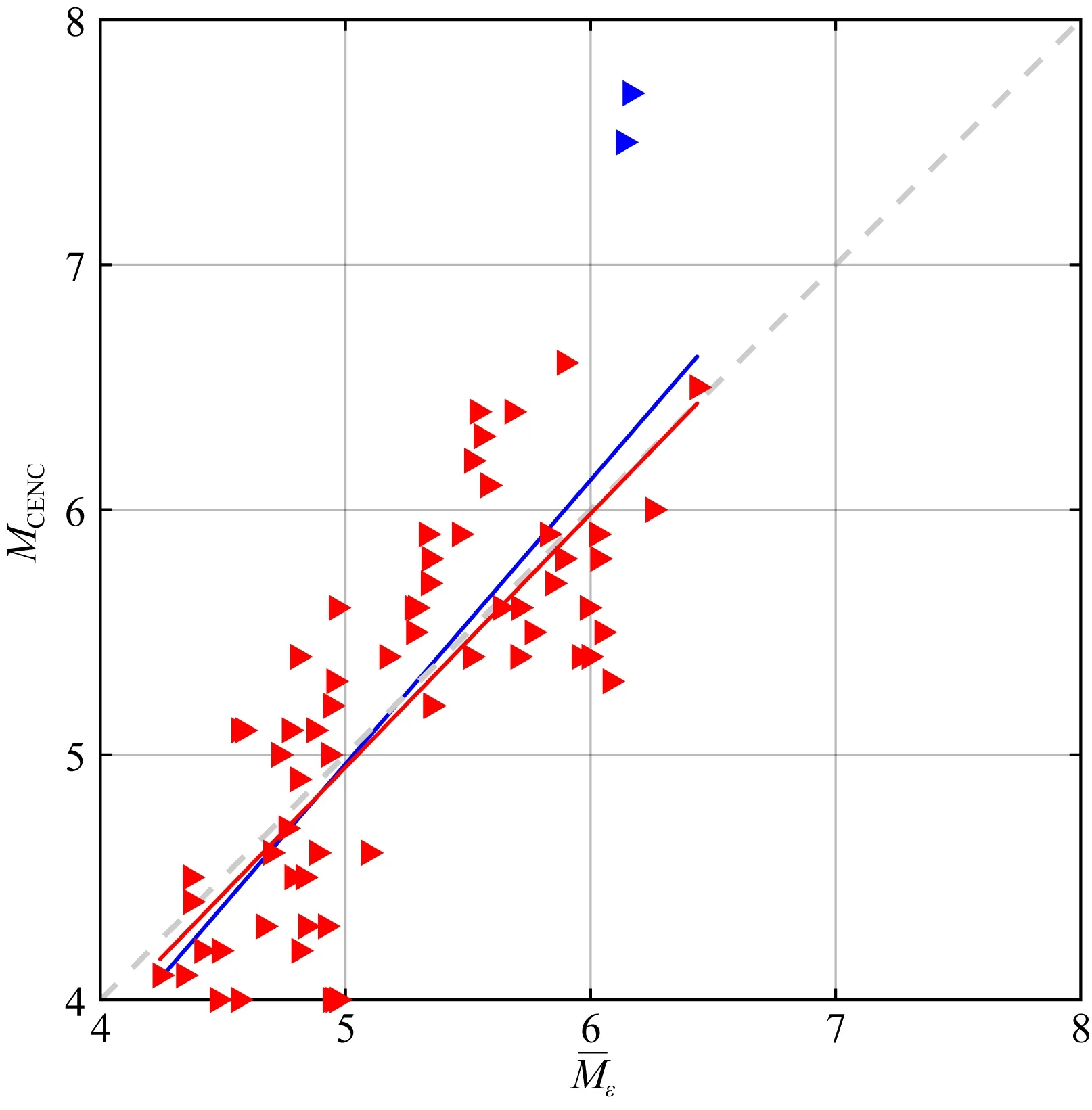
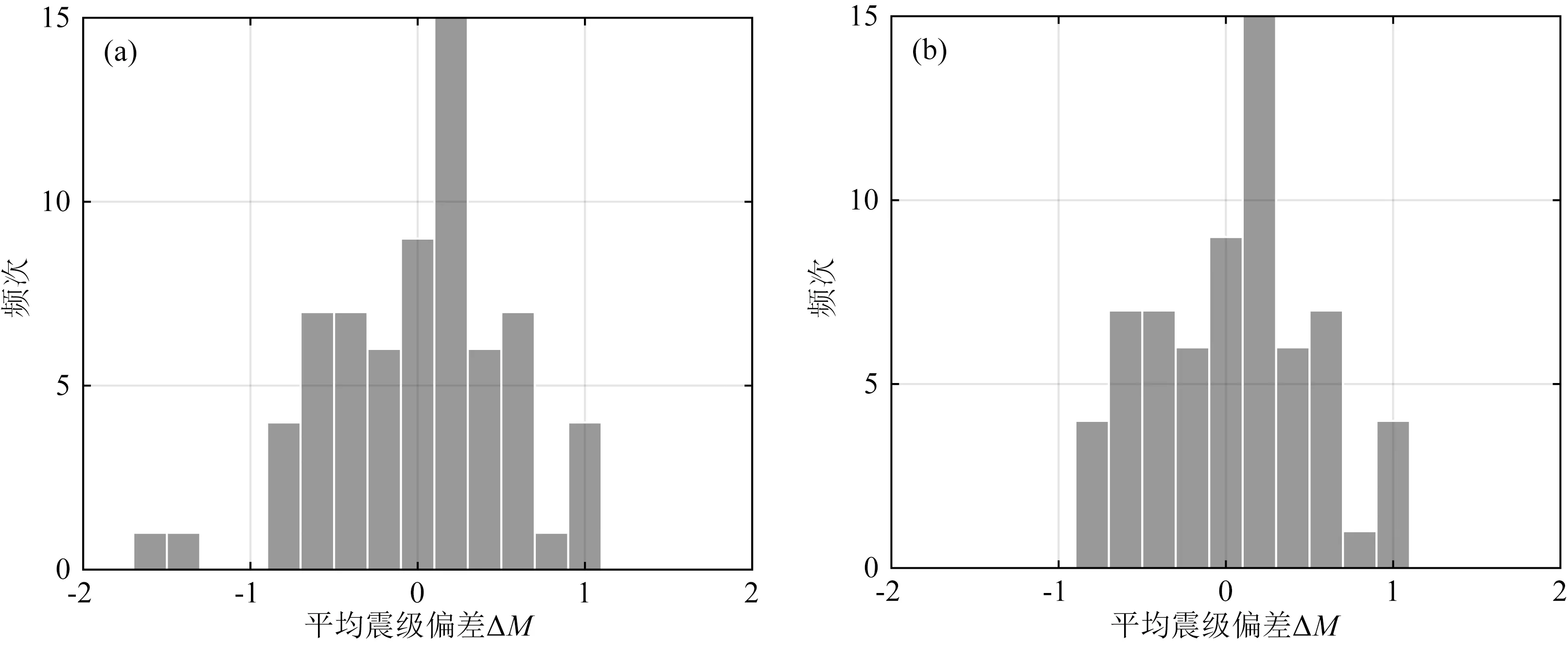
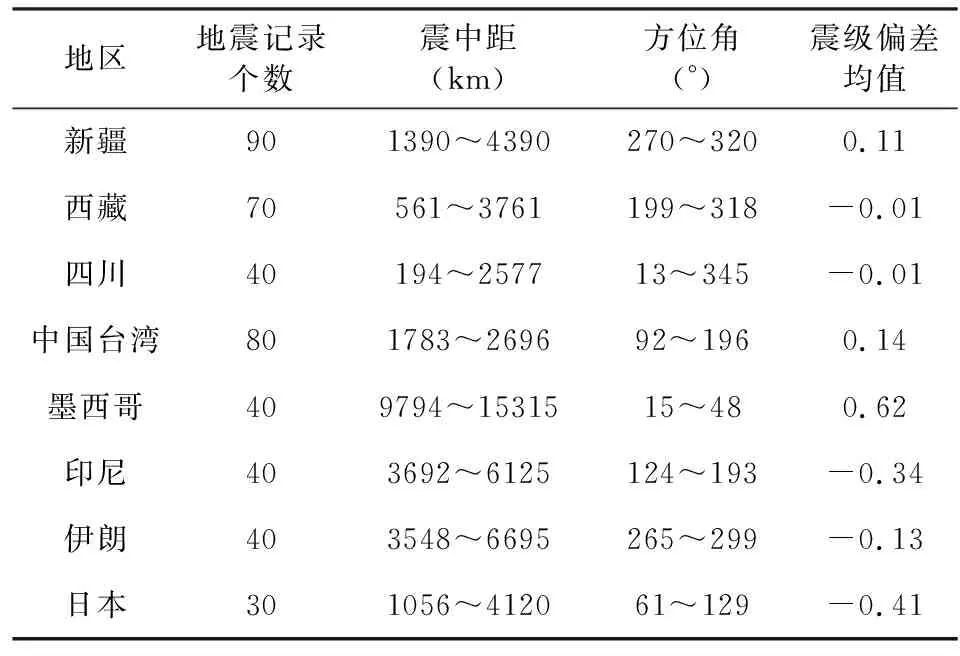
2°<Δ<130°, 3 s (1) 其中A表示水平向面波最大质点运动位移,单位为μm;T表示A对应的周期,单位为s;Δ表示震中距,单位为(°).这个公式自提出至今,一直得到广泛的应用.公式还反映了地震波周期(频率)对能量传递和震级确定的影响,这种影响在下面讨论应变幅度时会得到考虑. 四分量钻孔应变仪记录的是水平应变,x方向传来的平面波质点位移Ux为 Ux(x,t)=Acos(kx-ωt), (2) 质点运动速度为 (3) 应变与质点振动速度具有位相相反的类似波形: 图2 繁峙台记录的2020年1月19日新疆M6.4地震应变原始记录Fig.2 Original record of borehole strain at Fanzhi station of Xinjiang M6.4 Earthquake on Jan.19, 2020 图3 繁峙台记录的新疆M6.4地震钻孔应变记录滤波结果Fig.3 The filtering results of borehole strain records at Fanzhi station of Xinjiang M6.4 Earthquake =Esin(kx-ωt), (4) 其振幅E与位移振幅A的关系是 (5) 其中,ω表示角频率,λ表示波长,k表示波数,V表示波速. Mε=lgEmax+Xlg(Δ)+Y (6) 来计算应变震级Mε.其中Emax为钻孔应变记录到的最大水平应变,单位为纳应变(10-9).我们希望确定适当的X和Y,使得计算的应变震级Mε与中国地震台网中心发布的地震震级(记为MCENC)一致. 根据获取的最大主应变振幅及对应的震中距,用最小二乘法求(6)式中的参数X和Y.得到X=1.65、Y=1.43,因此应变震级的公式为 Mε=lgEmax+1.65lg(Δ)+1.43. (7) 值得注意,本公式X为1.65,公式(1)相应系数为1.66,反映了最大主应变和地震面波最大振幅随震中距衰减具有类似性的物理特征. 地震震级的测定需要把不同方位、不同震中距的大量台站测定结果进行算术平均.图4是对68个地震的每个地震用10个台站计算的应变震级平均值和中国地震台网中心给出的震级的比较图. 图4 中国地震台网中心震级MCENC与台站平均应变震级统计关系图蓝色三角形代表震级MS>7的地震,蓝色直线为68个地震的拟合线,红色直线为去掉震级MS>7的红色三角形地震的拟合线.Fig.4 Statistical diagram of magnitude MCENC published by the China Earthquake Networks Center and station mean strain magnitude The blue triangle represents the earthquake with magnitude MS>7, the blue line represents the fitting line of 68 earthquakes, and the red line represents the fitting line of the red triangle earthquake with magnitude MS>7 removed. 由图4蓝色拟合线可以看出,应变震级与面波震级大体存在线性关系.对二者进行回归分析,得到统计关系式、相应的均方差及相关系数如下: (8) 式中,σ为标准差,r为相关系数. 但由图4可以发现,当震级MS>7(蓝色三角)时,测得的最大主应变振幅不再增加,使得计算的应变震级不再随地震的增大而增大,出现震级饱和现象.去掉两个MS>7的地震事件,对地震面波震级与计算的台站平均应变震级进行回归分析(图4中红色拟合线),得到统计关系式、相应的均方差及相关系数如下: (9) 图4中红色拟合线显示,由10个台站测定的平均应变震级结果与中国地震台网中心震级的相关直线基本接近理想情况45°直线,线性相关系数为1.03.由图4可以看出,在4~6.5震级范围内,二者有较好的相关性. 为了进一步对所得公式进行检验,我们选取了永胜、湟源两个台站记录到的另外25个地震波数据,并计算最大主应变振幅以及震中距.按照应变震级公式(7)计算得到对应地震的应变震级平均值,与中国地震台网中心给出的面波震级进行比较如图5. 图5 中国地震台网中心震级MCENC与检验数据台站平均应变震级统计关系图Fig.5 Statistical diagram of magnitude MCENC published by the China Earthquake Networks Center and station mean strain magnitude of test data 对二者进行回归分析,得到统计关系式、相应的均方差及相关系数如下: (10) 说明将已有公式(7)、(9)运用到实际是成功的. 由于地震波辐射具有方向性,与震源破裂扩展方向和破裂形式有关,并且不同震中距离的传播路径上介质不均匀,存在不同的衰减和频散.不同台站台基性质也不同,所以不同台站对同一地震测定的震级会不同,同一台站记录不同方位地震时也有不同反应(Von Seggern, 1970;郭履灿等,1986;陈运泰和刘瑞丰,2004).因此,计算一个地震震级时需要对该地震多台震级的测定进行算术平均,并通过计算各个台站测定的单台震级和多台平均震级以及与中国地震台网中心公布的震级的偏差、总的平均偏差和总的标准差,对各个台站计算的震级的可靠性进行评估、分析(李雪英等,2004). 对于某个地震j(共N个地震)的M个台站平均震级为 (11) 第i个台站(共M个台站)的震级偏差为 (12) (13) 标准差为 (14) 应变台站测定的第j个地震的平均震级与中国地震台网中心发布的地震震级之间的偏差为 (15) (16) 标准偏差为 (17) 除受震源机制、地震波传播路径的影响,处在不同方位、不同震中距的地震台站测定的震级会有一定的偶然偏差.地震台站由于台基等因素会造成系统偏差,这种偏差需要校正(陈培善和秦嘉政,1982).根据公式(11)、(12)可以由10个应变台站计算得到68个地震震级的算术平均值,并计算各个台站测定的单台震级和10个应变台站平均震级的偏差. 表3 各个台站的震级平均偏差和标准差Table 3 Mean deviation and standard deviation of magnitude of each station 图6 各台站平均震级偏差图Fig.6 Diagram of mean magnitude deviation of each station 差究竟是与什么因素(例如岩性、构造、地形等)有关,有待今后深入研究. 台站校正是震级测定中十分重要的一环,对于一个地震台站,如果测定震级总是偏大或偏小,说明该台站的震级测定存在问题,需要进行校正.Gardini等(1997)在对地中海震级标定时就提到需要对东欧地区的台站引入静态台站校正项.震级偏差反映了台站的台基场地差异,表3列出了本文各个台站的震级偏差校正参考值. 针对台站震级偏差进行台基校正后,首先对单台震级偏差与台网平均震级偏差的分布情况进行分析. 图7 台站单台应变震级Mε与平均应变震级震级偏差统计图Fig.7 Statistic chart of magnitude deviation between single station strain magnitude Mε and mean strain magnitude 一个地震震级的测定需要不同方位台站、不同辐射能量测定震级的平均值.严格来说,我们起码应该有方位角相差90°以上的台站记录求平均震级(Rösler and Van Der Lee, 2020).目前应变台站不多,本研究中10个台站记录的68个地震,共有20个地震事件的方位角最大差值大于90°,所以需要观察震中方位角是否有影响. 为了进一步按照震中方位角以及震中距分布分析震级偏差情况,如图8为极坐标系上以各钻孔应变台站为中心,相对于台站不同方位角的地震震中分布图,震级偏差ΔM>0(红色圆圈),ΔM<0(绿色圆圈)分别代表每个台站测定的地震震级相对于10个台站对应应变平均震级的偏大和偏小.通过对图中震级偏差结果进行检查,发现台站测定的不同震中距(0~17000 km)和不同方位地震的应变震级偏差随震中距和方位角变化基本呈随机正负分布. 图8 台站各方位角区间的地震震级偏差分布图红色实心圆代表震级偏差大于0.5,红色空心圆代表震级偏差介于0~0.5,绿色空心圆代表震级偏差介于-0.5~0,绿色实心圆代表震级偏差小于-0.5. R为震中距,单位为km.Fig.8 Distribution of magnitude deviation with different azimuth interval for stationsThe red solid circle represents magnitude deviation more than 0.5, the red hollow circle represents magnitude deviation between 0 and 0.5, the green hollow circle represents magnitude deviation between -0.5 and 0, and the green solid circle represents magnitude deviation less than -0.5. R is epicentral distance and the unit is km. 下面以中国地震台网中心发布的地震震级为参照标准,对台站校正后的地震应变震级与中国地震台网中心震级的震级偏差进行统计,如图9a.计算得到,68个地震震级偏差的均方差为0.52,但分布有偏不对称,中位数为0.09.去除两个7级地震,得到的震级偏差分布如图9b.均方差降低为0.47,表明震级偏差的离散度降低,中位数为0.10.国际上对于0.3级以内的偏差认为是在误差范围之内.通过计算,发现应变台站平均震级和中国地震台网中心公布的震级基本吻合.除去7级地震,其余66个地震的震级偏差中-0.3≤ΔM≤0.3占45%.计算的68个平均应变震级结果中,有37个地震的震级偏大,震级偏小的有31个,总体来说,正偏差的个数较负偏差个数略多. 图9 台站平均应变震级与中国地震台网中心震级MCENC震级偏差统计图(a) 68个地震震级偏差; (b) 去除M>7的66个地震震级偏差.Fig.9 Statistics chart of magnitude deviation between station mean strain magnitude and magnitude MCENC published by the China Earthquake Networks Center(a) The magnitude deviation of 68 earthquakes; (b) The magnitude deviation of 66 earthquakes with magnitude M>7 removed. 如果把10个台站对68个地震的全部应变震级计算结果与这68个地震中国地震台网中心给出的各自地震震级的偏差也做频度统计图,则如图10a.震级偏差平均值为-0.0002,均方差为0.63,中位数为-0.01,震级偏差范围为-2.1~3.3.去除7级地震,震级偏差分布如图10b,发现分布曲线形态基本呈正态分布,以0为对称轴.震级偏差平均值为0.04,均方差为0.59,中位数为0.02,震级偏差范围为-1.7~3.3,其中-0.3≤ΔM≤0.3占40%. 下面分别按照不同震中距、不同方位角以及不同地区对震级偏差进行分析.有研究人员发现,使用布拉格(Prague)公式确定的欧洲地区的面波震级MS与记录台站距离的关系不大(Ambraseys and Free, 1997).新西兰地震面波震级的偏差与台站到地震的距离有微弱关系(Rhoades and Dowrick, 1999).以中国地震台网中心公布的地震震级为参考,对台站校正后的震级偏差与震中距的关系进行统计.根据震中距的不同,地震可以分为近震(100 km≤Δ<1000 km)、远震(1000 km≤Δ<105°)、极远震(Δ≥105°).以此分类,统计10个台站测定的68个地震震级偏差与震中距的关系(表4),可以发现,震中距对震级偏差影响不大. 表4 不同震中距震级偏差统计结果Table 4 Statistical results of magnitude deviation with different epicentral distances 震级受地震波传播路径、台站台基等影响,面波振幅大小受传播路径影响较大.将所选地震划分为4个方位,统计10个台站记录的68个地震的震级偏差平均值与对应的不同范围方位角的关系(表5).整体上,各个方向的地震震级偏差结果相差不大,主要介于-0.1~0.1. 表5 不同方位角震级偏差统计结果Table 5 Statistical results of magnitude deviation with different azimuths 应变台站较多记录到中国新疆、西藏、四川、台湾以及印尼、伊朗、日本、墨西哥等地区发生的地震,对不同地区的震级偏差进行统计(表6).从表6可见,墨西哥和日本、印尼地区的震级偏差较大,分别为0.62、-0.41、-0.34,其他地区的震级偏差与前文给出的震级偏差平均值较接近. 表6 不同地区震级偏差统计结果Table 6 Statistical results of magnitude deviation in different areas Howell(1981)注意到当地震能量达到一定程度后,面波震级、体波震级等均会在高震级出现震级饱和现象,只有矩震级不会出现饱和.本文在应变震级研究中也发现了震级饱和,虽然震例有限,但这两个MS>7地震,计算得到的应变震级不再随地震的增大而增大.这不仅关系到应变震级确定的问题,由于地震的动态触发问题与接收断层上应变波动最大振幅确定的最大动态库仑应力有关,因此这也涉及7级以上大地震远震动态触发危险性的研究.今后需要搜集更多震例进行深入研究. 图10 台站单台应变震级Mε与中国地震台网中心震级MCENC震级偏差统计图(a) 680个震级偏差; (b) 去除M>7的660个震级偏差.Fig.10 Statistics chart of magnitude deviation between single station strain magnitude Mε and magnitude MCENC published by the China Earthquake Networks Center(a) 680 magnitude deviations; (b) 660 magnitude deviations with magnitude M>7 removed. 如果振幅的确存在震级饱和现象的话,那么钻孔应变地震波持续时间与震级是否有关就是另一个值得调研的问题.常规的地震波记录长度与地震震级大小有关,震级越大,持续时间则越长.根据Bisztricsany(1958),地震持续时间指从第一个地震波开始,直到波列振幅减小到至少其最大记录值的10%.而Castello等(2007)则指出震级与地震波持续时间之间存在一定的关系:Md=2.49lg(T)-2.31+Sc.在钻孔应变地震波动记录中是否有类似规律、是否可以提供绕过震级饱和问题的途径,今后也值得进一步研究(陈启林等,2015). 本文研究表明,利用钻孔应变地震波数据确定地震震级是可行的.它不仅是对目前测定地震震级在方法上的补充,而且这种对水平应变的超宽频带的直接记录为应力触发的研究也提供了宝贵的直接观测资料,应该可以成为传统地震学记录的有价值的延拓.因此,十分有必要加强这个方向上的研究,争取早日在未来钻孔应变台站的规范中,把采样率确定为100 Hz;在台站日常工作中,逐渐增加对应变计的地震应变波动记录的分析,上传到省和国家地震中心纳入地震目录的编撰.在今后的研究中不仅应使用国内四分量钻孔应变台站的资料,对国外板块边界观测计划(Plate Boundary Observation,PBO)等达到资料要求的记录也可以进行分析.钻孔应变观测若能在月球、火星等类地行星上布设,如果能同时记录到月震和月球固体潮,也将有助于在行星物理学研究中取得创新成果. 致谢感谢三位匿名审稿人的中肯意见,使我们对文章有进一步改进.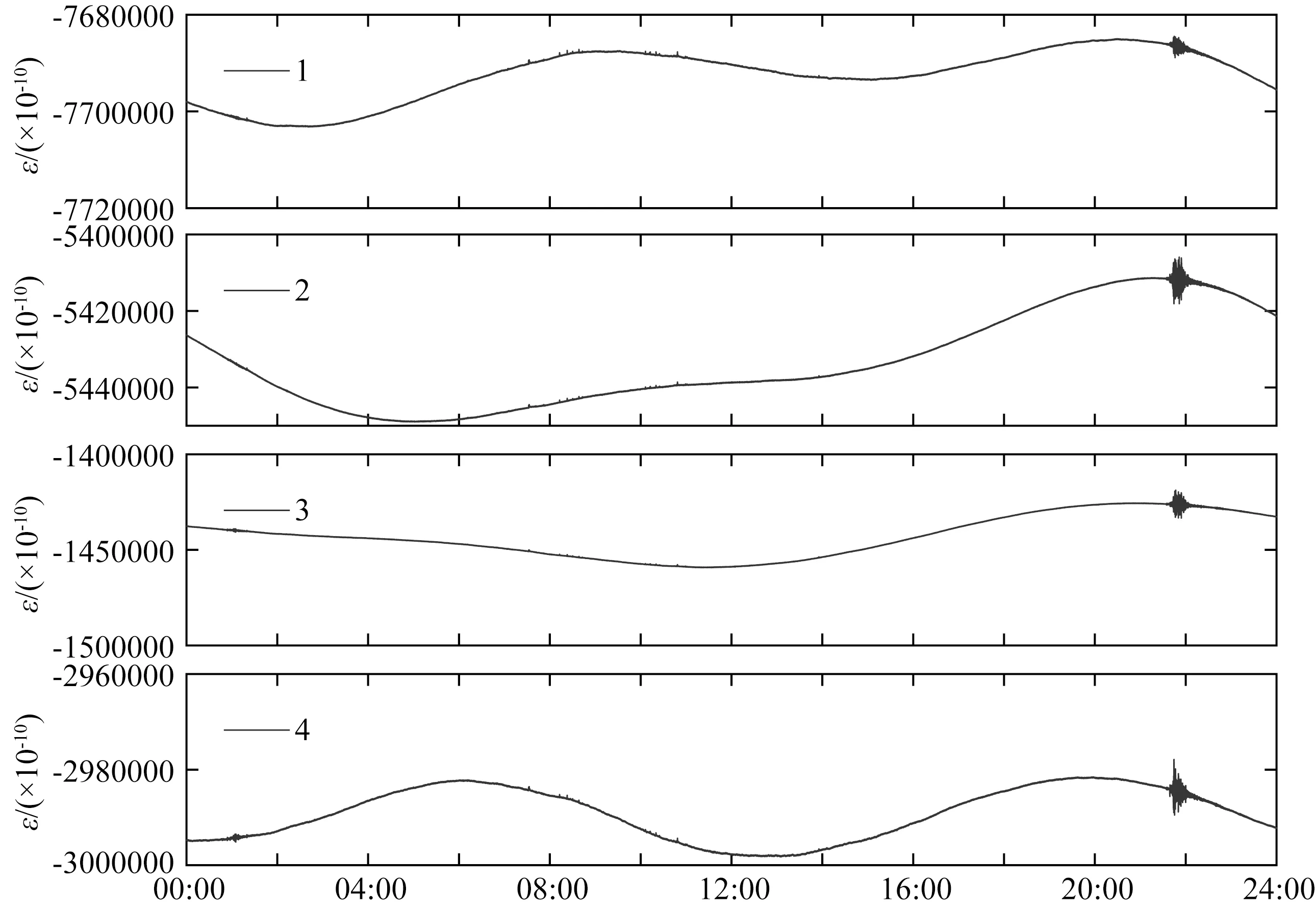




3 讨论
3.1 震级偏差计算


3.2 台站校正
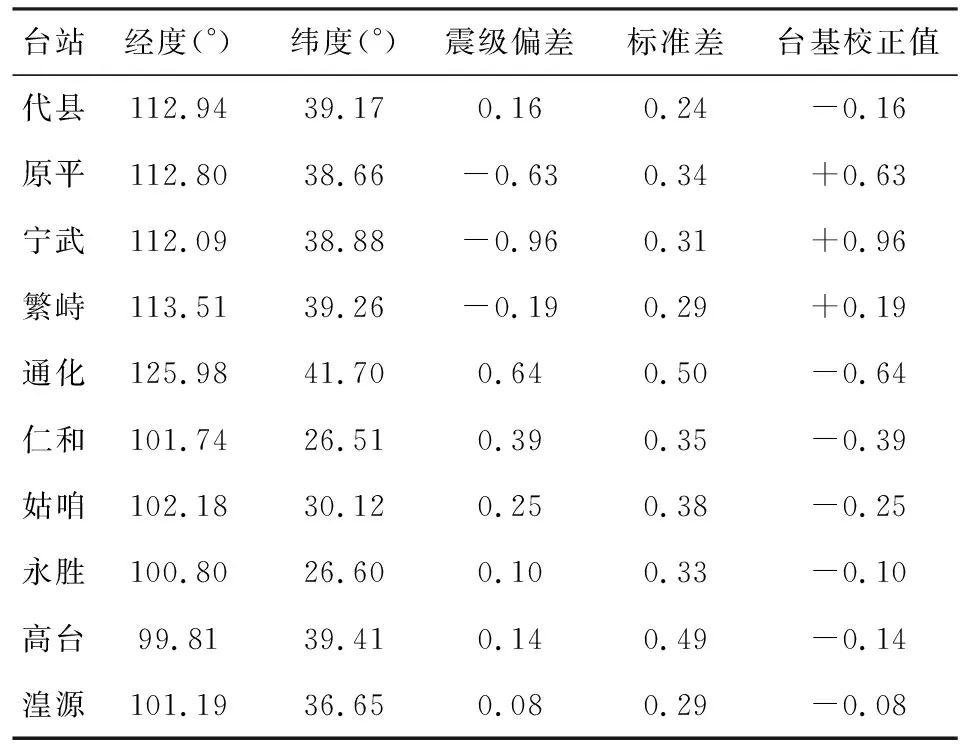

3.3 震级偏差分析





3.4 震级饱和问题

4 结论


