高阶Lagrange中值定理“中值点”的渐近性

苑倩倩， 路振国， 任立顺

(1.信阳学院 数学与统计学院，河南 信阳464000； 2.信阳师范学院 教务处，河南 信阳464000；3.周口师范学院 数学与统计学院，河南 周口466000)

1 引 言

自1982年B. Jacabson[1]和A. G. Azpeitia[2]提出积分中值定理及Taylor公式“中值点”的渐近性以来，许多数学工作者开始研究各种微积分中值定理“中值点”的渐近性，相继有许多研究成果.如文献[3-8]讨论了积分中值定理“中值点”的渐近性，其中张宝林[3]推广了B. Jacabson[1]的结论，得到了积分第一中值定理“中值点”ξx必满足：

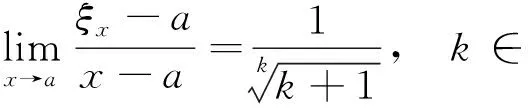
杨彩萍等在文献[5]中得到了推广的积分第一中值定理“中值点”ξx必满足：

文献[9-20]讨论了各种微分中值定理“中值点”的渐近性，其中李元中、冯汉桥在文献[9]中得到了关于高阶Larange中值定理“中值点”的渐近性，“中值点”ξ满足：

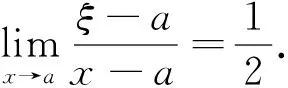
李治远在文献[19]中讨论了几类初等函数的拉格朗日中值定理中值点的确定方法，并给出了从低阶到高阶可导函数的拉格朗日中值点的渐近性.这些对高阶中值公式“中值点”的渐近性研究中，f(n+1)(a)≠0是定理成立的关键性条件，当f(n+1)(a)=0或f(n+1)(a)不存在时，至今没有见到更好的结果.本文将借助Stirling数这个工具，从

(i)f(n+1)(a)不存在；

(ii)f(n+i)(a)=0(i=1，2，3，…，m-n-1)，而f(m)(a)不存在，

两个方面来讨论高阶Lagrange中值定理“中值点”的渐近性.

2 几个引理

引理1设f(x)在点a的某邻域内n阶可导，记

若存在0<α<1， 使得

f(x)=Pn(x)+g(x)(x-a)n+α，

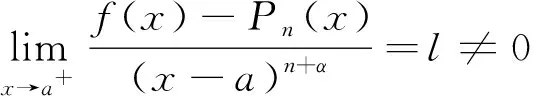
进而

f(x)=Pn(x)+l(x-a)n+α+o((x-a)n+α)=Pn(x)+(l+o(1))(x-a)n+α，

因f(x)在点a的某邻域内有n阶连续导数，则g(x)(x-a)n+α在点a的该邻域内也有n阶连续导数，且(g(x)(x-a)n+α)(n)=f(n)(x)-f(n)(a).下证

因为

即

所以

引理2[21]∀m，n∈+，有

其中S(m，n)称为Stirling数.

引理3设

则∀α>1，有

S(α，n)=S(α-1，n-1)+nS(α-1，n)，

且S(α，1)=1，S(α，0)=0.

证∀α>1，

S(α-1，n-1)+nS(α-1，n)

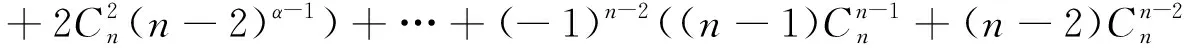
=S(α，n).

引理4[22](Lagrange高阶微分中值定理) 设f(x)在点x0的某邻域U(x0)内具有n阶连续导数，则∀x∈U(x0)，存在ξ∈U(x0)，使得

(1)

3 主要结果

定理1设f∶[a，b]→具有n阶连续导数，f(n+1)(a)不存在，若存在0<α<1，使得

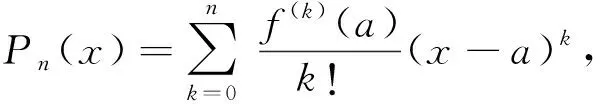
证因为

由引理1知:存在函数g(x)，使得

f(x)=Pn(x)+g(x)(x-a)n+α，

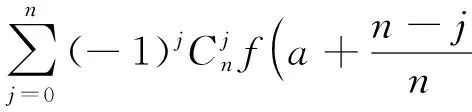
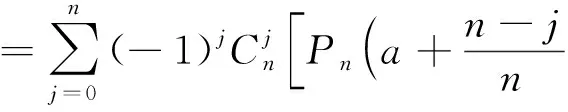
(2)

又因为

f(n)(x)=f(n)(a)+(g(x)(x-a)n+α)(n)，

所以

(3)

由引理2知

所以(2)式变为

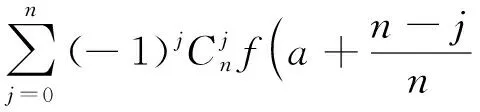
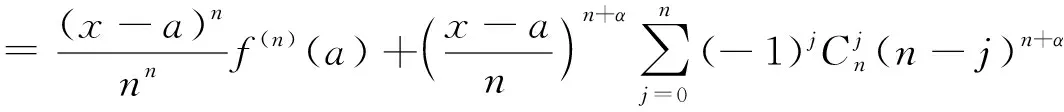
(4)

由引理4的(1)式知，(3)与(4)相等.即

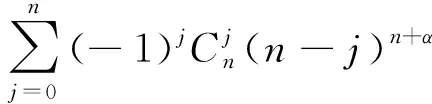
(5)

因为x→a+时，ξ→a+，所以，(5)式两边当x→a+时，利用引理1得

(6)

定理2设f∶[a，b]→R具有n+k阶连续导数，且f(n+i)(a)=0(i=1，2，…，k)，f(n+k+1)(a)不存在.若存在0<α<1，使得

则∀x∈(a，b)，存在满足引理4的ξ∈(a，x)， 使得

证由引理1可得，f(x)在点a处n阶Taylor展式为

(7)

将f(n)(x)及(7)式代入引理4中的(1)式，并利用引理2得

(8)

(9)

由(8)式及(9)式得

(10)

因ξ∈(a，x)，所以x→a+时，有ξ→a+， (10)式两边当x→a+时，有

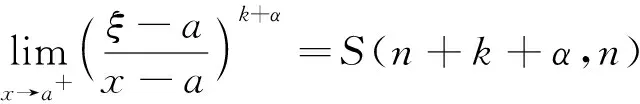
由文献[13]知

所以

(11)

推论1设f在[a，b]上连续，在点a处不可导，若存在0<α<1，使得

(12)

推论2设f∶[a，b]→具有n+k阶连续导数，f(n+k+1)(a)不存在，若存在0<α<1，使得

则对任意x∈(a，b)，n阶Taylor中值点ηx∈(a，x)满足

证由定理2的证明知

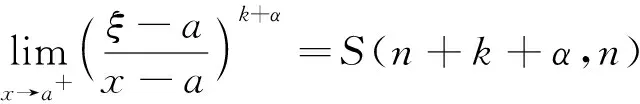
推论3设f在点a具有m-1阶导数，且f(i)(a)=0(i=1，2…，m-1)，f(m)(a)不存在.如果存在0<α<1，使得

注 (i) 推论1是文献[3]结论的推广，是文献[4]当g(x)=1时的结论.

(ii) 推论2是文献[13]定理1的结果.

下面结合一个具体的例子来验证文中结论的正确性.

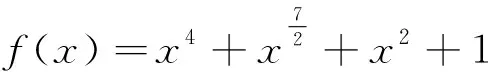
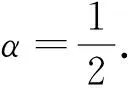
由定理1知

所以中值点的的渐近估计式为

(13)

所以中值点的的渐近估计式为

(14)

接下来，利用Lagrange高阶微分中值公式来检验定理的正确性.

由于

当n=2时，利用Lagrange高阶微分中值公式(1)， 得

即

(15)

此时(14)式中的中值点ξ的渐近估计式满足(15)式.

当n=3时，利用Lagrange高阶微分中值公式(1)， 得

即

(16)

此时(13)式中的中值点ξ的渐近估计式满足(16)式.定理1及定理2结论的正确性得以验证.

4 结 论

本文在已有的关于高阶Lagrange中值定理“中值点”渐近性研究的基础之上，利用Stirling数研究了当f(n+1)(a)=0或f(n+1)(a)不存在时，高阶Lagrange微分中值定理的“中值点”的渐近性，并给出了渐近性估计式.与利用Lagrange高阶微分中值公式求解相比，本文中给出的求解方法更简便.

致谢在此对相关参考文献给予本文的启发与思考，以及审稿人给出的宝贵建议表示衷心的感谢！