数学符号的信息暗示作用及相应教学策略探析

□王 洋

（桐乡市茅盾中学，浙江桐乡 314500）

数学符号作为数学抽象思维的产物，能以简单的形式揭示出数学的一般规律.数学符号中往往暗示条件、结果、方法等，如果教师能在教学中运用它所暗示的信息，那么就能启发学生解题，优化解题的过程.以下笔者通过具体试题分析来阐述相关问题.

一、数学符号的信息暗示作用

在数学解题的过程中，学生可通过观察题目中数学符号所暗示的信息源，激活储存在脑海中的知识与经验，并通过联想回忆获得解题思路，找到题目的突破口.这样很多所谓的难题、压轴题就可迎刃而解了.

（一）元素符号的暗示作用

1.字母符号的暗示作用

在立体几何、解析几何等数学解题过程中，字母符号给我们解题带来很多便捷.然而，经调查发现，学生对部分字母的敏感程度是不一样的.在解题时如果改变个别重要字母，学生会产生不同的思维活动.

例1如图1，在等边三角形ABC外有一点，满足AD=AC，求∠BDC的度数.

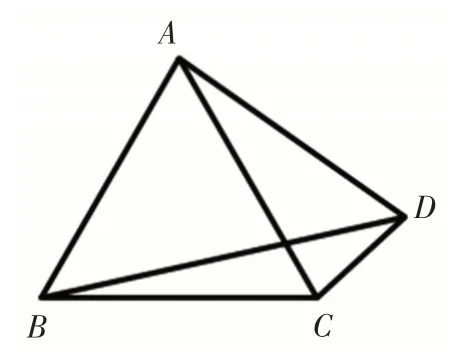
图1

对这一试题，笔者在实践中发现，如果把题中的字母A改为字母O，学生更能够联想到用圆周角定理来解决，这说明字母O能激发学生的联想，对解题能起到暗示作用.

2.数字符号的暗示作用

除了字母，有些数字也会给人灵感，诱发解题思路.

例2f(x)=Msin(ωx+φ)（M、ω、φ均为常数，M＞0，ω＞ 0,0 ≤φ≤ π）的部分图像如图（图略）所示，其中A、B两点之间的距离为5，那f（-1）=（）

A.-2 B.-1 C.2 D.-1或2

因为A、B两点之间的距离为5，A、B两点间纵坐标的距离为4，根据4、5 这两个数字的暗示，此题可以用勾股定理来解，即A、B两点间横坐标的距离为3.所以，由最小周期T=6=即可求得ω.

二、用好数学符号信息按时作用的教学策略

数学符号的暗示有一定的隐蔽性，教师在教学中要引导学生重视对暗示信息的捕捉，锻炼思维能力，进而提高解题能力.

（一）将数学文字叙述语言转化为数学符号语言

如果不能准确地将叙述性语言转化为数学符号语言，那么就谈不上数学的应用.学生将叙述性语言转化为数学符号语言，也是锻炼数学思维能力.通俗的自然语言和简练的数学语言是密不可分的，对于阅读量大、看不懂的题目，如果能用数学语言去解释，往往就能看出题目中隐含的信息，帮助理清解题思路.

例9某企业生产甲、乙两种产品，已知生产每吨甲产品要用A原料3吨，B原料2吨，生产每吨乙产品需要用A 原料1 吨，B 原料3 吨.销售每吨甲产品可获得利润5万元，每吨乙产品可获得利润3万元.该企业在一个生产周期内消耗A 原料不超过13 吨，B 原料不超过18吨.那么该企业可获得的最大利润为（）

A.12万元 B.20万元

C.25万元 D.27万元

这样一道题目，去掉外包装，对其“抽丝剥茧”，可将自然语言转化为符号语言：设生产甲产品x吨，乙产品y吨，使得利润z最大.如此，列出表格，写出约束条件并画出可行域，即可解题.

（二）经历数学符号的建构过程

近几年高考卷的最后一题，往往是关于圆锥曲线或是函数这类综合性比较强的题目，且所占分值比较大.教师应加强对这内容的重视.关于函数，一次函数、二次函数、反比例函数、指数函数、对数函数是高中学生所熟悉的.研究近年来的数学高考试卷可以发现：函数类题目一般是对我们熟悉的函数进行加减乘除的组合.因此，在教学中教师可以让学生经历知识由简单到复杂的组合过程，启发学生得出哪几种组合方式是最常见的也是最合理的，并提出对相应组合方式的处理方法等.如教师可以这样引导：

当学生摸清了这类函数题的解题套路，再遇到类似的组合时，符号的暗示和刺激就会使他们回忆、整理脑海中的知识.

例 10已 知f(x)=x2+ax+blnx. 若b=a2，f（x）＞0在x＞0恒成立，求a的取值范围.

如果学生在解题之前通过整理和交流经历了知识的建构过程，那么根据题目的暗示，就能结合已有知识得出，这一类恒成立问题一般有两种解题思路：一是参变分离法，二是“一个函数”思想.解此题用参变分离法有一定困难，那么可以用第二种方法求函数的最值.

（三）加强数学阅读，优化变式教学

学生的数学阅读量少，从某种程度上说会影响学生的转化、翻译能力.变式教学有利于学生促进对陈述性知识的转化，并通过信息的增加、冲突引起有效内部语言，提高思维能力.

这样将各个知识点都串接起来，拓展学生的思维能力，在变中求不变，可以加强学生提取符号暗示信息的能力.

（四）加强数学符号的类比

通过寻找题目或命题间的异同，可以培养学生对数学符号的敏感度，进而提高学生提取暗示信息的能力.

例12已知则这个数列的前30项中最大项和最小项分别是（ ）

A.a1,a30B.a1,a9C.a10,a9D.a10,a30

（五）注重实质，淡化形式

学习符号最大的弊端就是只记住符号的形式而不了解问题的本质，这容易导致不能“活用”，故教师在教学中除了要培养学生的符号感外，还要培养学生对文字语言的理解能力.