优化的维纳滤波算法在心音信号中降噪的应用

王佳佳, 周克良

(江西理工大学 a. 能源与机械工程学院, b. 电气工程及其自动化学院, 江西 赣州 341000)

由于硬件自身的特点,医学设备虽然可以检测到人体的心音信号,但是对于噪声却不能进行自我的判断与消除,而这些问题就需要智能算法进行弥补.

智能算法可以针对病人的心音信号和外界噪声的特性,进行自我分析与判断,最后进行降噪.本文所研究的对象是二尖瓣心音信号,针对病人的二尖瓣心音信号来判断病人的病情.

1 二尖瓣心音信号降噪的研究现状

据分析,二尖瓣心音信号的噪声主要来自于周围环境中的噪声、工频噪声(50 Hz)、病人与周围物体的摩擦、仪器本身含有的噪声(35 Hz)等.这些噪声会吞没二尖瓣心音信号的有用信息,进而影响医学专家的判断.目前对于二尖瓣心音信号的降噪问题,国内外学者已通过采用小波分析、奇异值分解、混沌时间序列、自适应算法等进行了研究[1-2],且已取得一定成效,但同时存在处理高频信号有失真、算法收敛性和实验精度不高等不足[3-4].

维纳滤波(wiener filtering)是一种基于最小均方误差准则对平稳过程的最优估计器[1],该算法作为一种滤除噪声或干扰以提取有用信息的滤波器,在降噪方面具有十分重要的应用价值.但同时它采用FFT变换进行时域分析,这对于处理非平稳类型的信号存在分辨率较低等缺陷.鉴于此,本文在维纳滤波算法的基础上,提出一种优化的维纳滤波算法对二尖瓣心音信号进行降噪,以减少二尖瓣心音信号中的残留问题,同时提高心音信号的分辨率.

2 二尖瓣心音信号的降噪原理

2.1 EMD分解原理

EMD算法的原理是对采集的心音信号首先进行EMD分解,得到有限个模态IMF分量[2-3],由于心音信号主要集中在低频部分,因此舍去前三阶的模态IMF分量,可减去一部分二尖瓣心音信号中夹杂的高频率的外界噪声,保留EMD分解中的低频率IMF分量[5-8].

2.2 离散S变换维纳滤波算法

首先,定义采集的二尖瓣心音信号

y(t)=x(t)+d(t).

(1)

式中:x(t)表示纯二尖瓣心音信号;d(t)为心音中所夹杂的外界噪声信号;y(t)为实际的二尖瓣心音信号.对二尖瓣心音信号进行离散S变换得

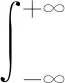
(2)

本文所有的高斯窗函数为

定义域半径为

Rd=min[5α/f,L].

窗长为[-Rd,Rd],记k=[Rd/T].进而可得高斯窗函数为

(3)

式中δ的值会直接影响到窗函数的形状,进而可调节S变换的分辨率.对于式(3)中δ的值取1/|f|.则S变换公式为

(4)

可导出维纳滤波算法中的数字滤波器[9-11]H(k):

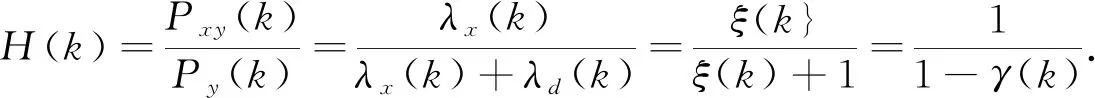
(5)

其中,Pxy是x(t)与y(t)的互功率谱密度,Py是y(t)的功率谱密度.进一步可导出维纳滤波的输出

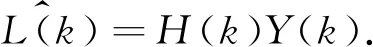
(6)

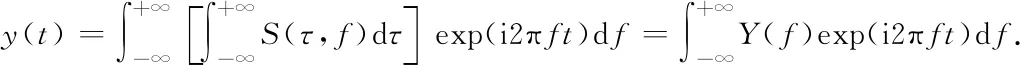
(7)

式中,Y(f)为y(t)的Fourier变换.

3 优化的维纳滤波算法

1) 对实际的二尖瓣心音信号进行EMD分解,可得到有限个IMF分量,本文将舍去前三阶的IMF分量(心音信号主要集中于低频信号中,前三阶IMF分量基本上都是高频信号),并进行重构二尖瓣心音信号.

2) 重构二尖瓣心音信号进行窗函数分帧,确定它的信号长度L,时间间隔T,和采样点数N=L/T.

3) 对窗函数的参数δ进行设置(δ是与频域无关的参数,在整个运算中只会取一个值.否则,可根据当前的频率进行调整),对于给定的频率f,0≤f≤1/2T,以及频率的采样间隔f、采样点数NF有HT(nT)=h(nT)exp(-i2πfnT).

4) 对于二尖瓣心音信号的频率按照采样点进行有序循环,计算出各个频率点处的S变换.

① 记fi=if.计算离散频率为f时,信号y(t)的调谐信号HT(nT)及窗函数w(mT,fi);

② 根据公式

计算出频率fi所对应的S变换谱线;

③ 增加i,返回3),直到i>NF,便可得到信号在所有频率点处的S变换谱线.

5) 求出所有的S变换谱线之后,调用VAD函数求出噪声帧和心音帧,对于噪声帧,计算出噪声平均幅值谱,即λd.

6) 求出后验信噪比γi(k)和先验信噪比ξi(k),并求出维纳滤波器的传递函数Hi(k).

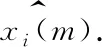
正常心音信号降噪之后的结果如图1、图2所示.

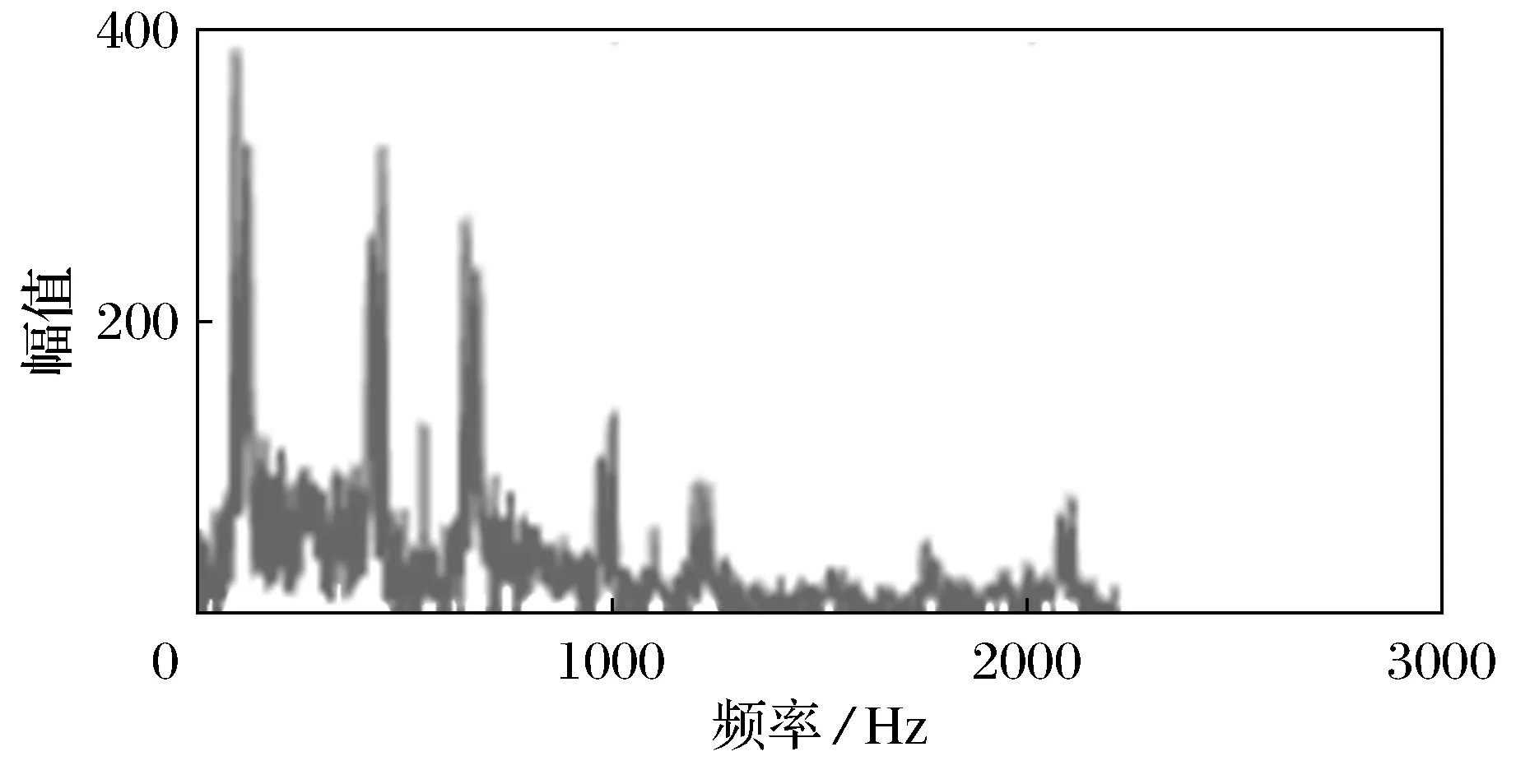
图1 含噪心音信号的幅频谱Fig.1 Spectrogram of a noisyheart sound signal

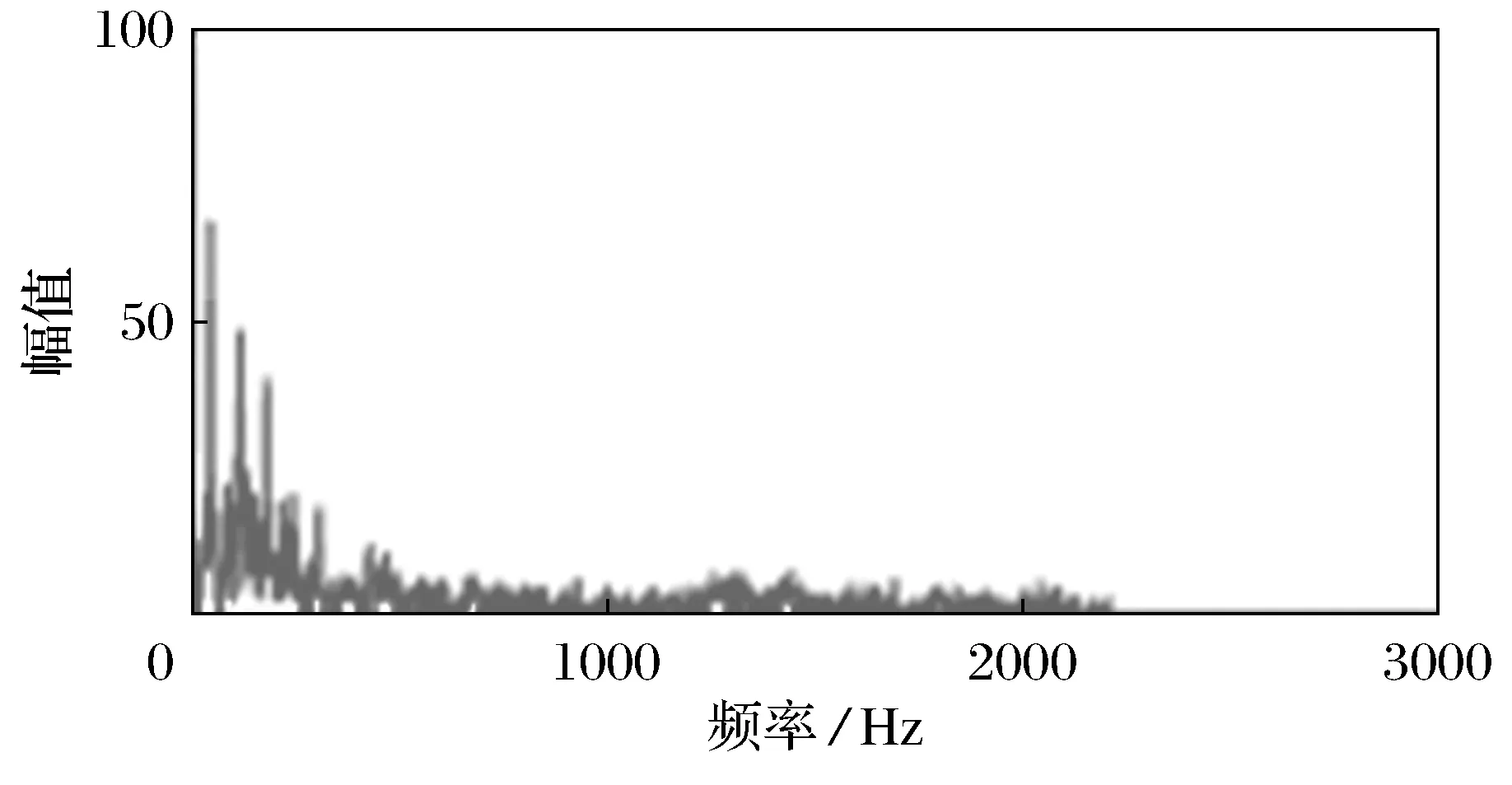
图2 降噪之后的正常心音信号的幅频谱Fig.2 Spectrogram of normal heart sound signal after noise reduction

由图1、图2分析对比可得,心音信号的频率主要集中于低频信号中,优化的维纳滤波算法有效的降低了正常心音信号中的噪声,进而提高了信噪比.

4 分析

本文从某医院采集的心音数据包括:二尖瓣狭窄(心房心颤)、二尖瓣狭窄(严重)、二尖瓣狭窄(心动过速),这3种心音信号采样的频率为4 000 Hz,量化精度为16 bit.

将优化的维纳滤波算法用于采集的心音信号,可有图3～图5结果.

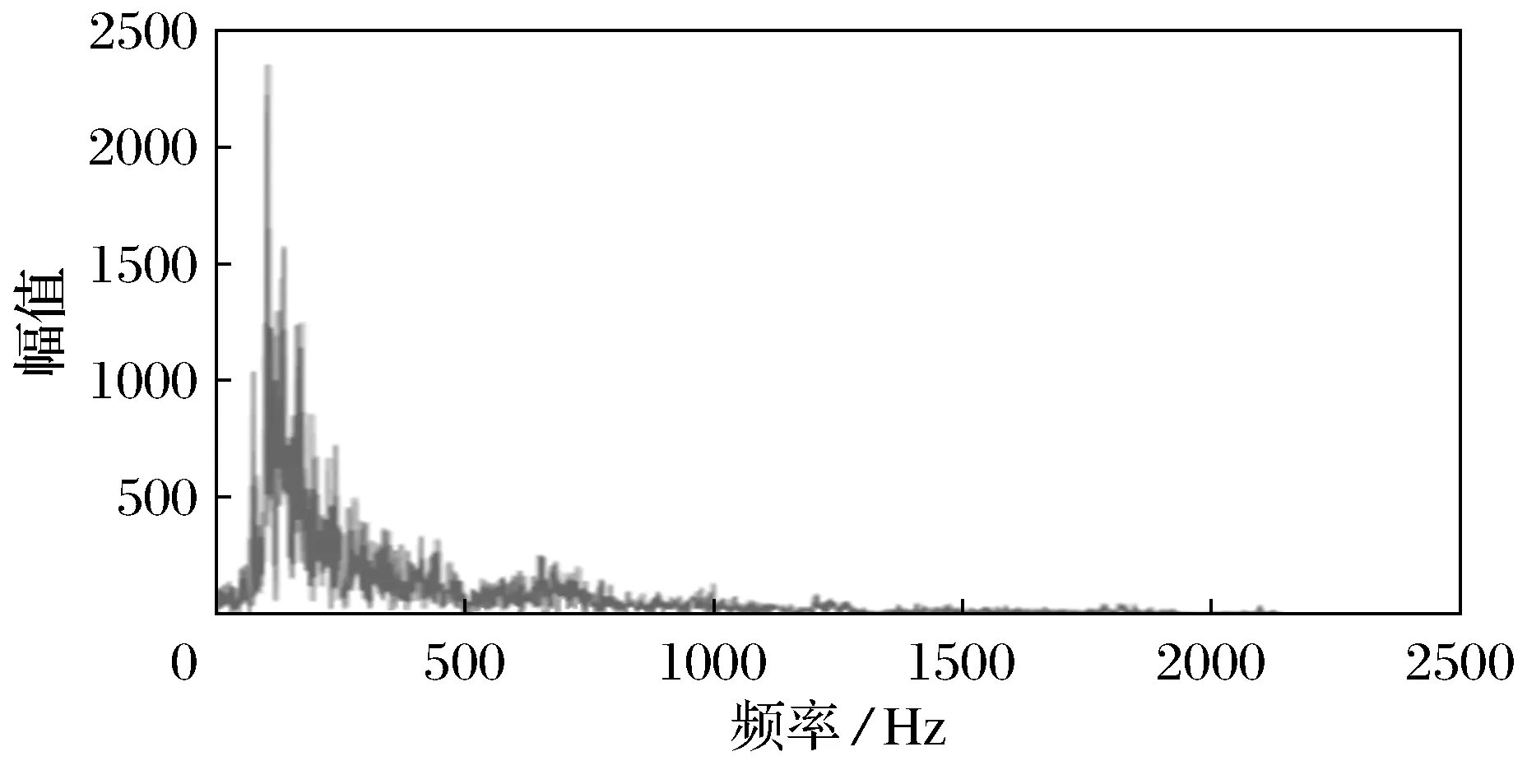
图3 纯二尖瓣狭窄(心房心颤)幅频谱Fig.3 Spectrogram of pure mitralstenosis (atrial fibrillation)

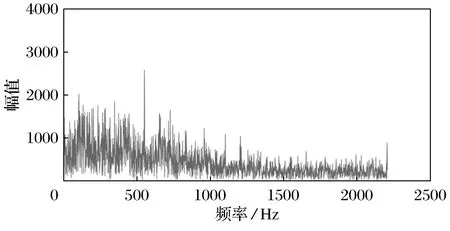
图4 含噪二尖瓣狭窄(心房心颤)心音幅频谱Fig.4 Heart sound amplitude spectrogram of noisy mitralstenosis (atrial fibrillation)

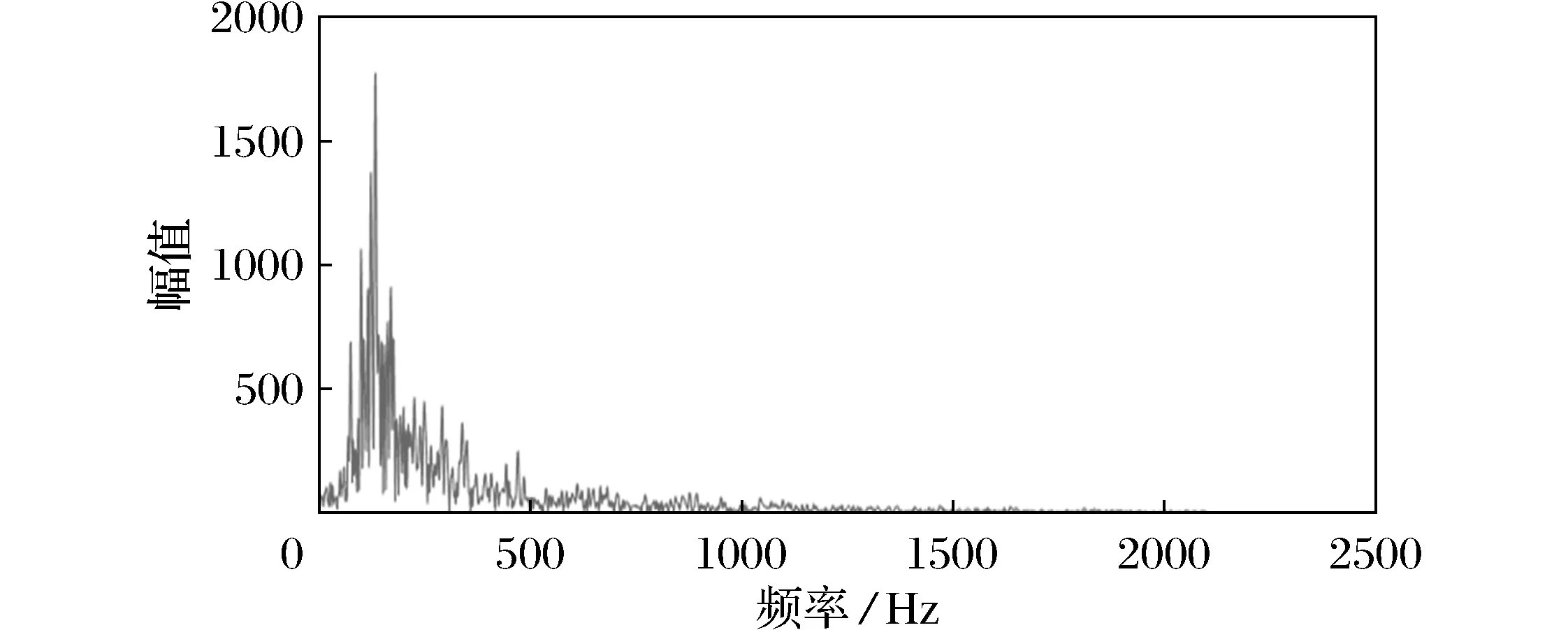
图5 降噪之后的二尖瓣狭窄(心房心颤)幅频谱Fig.5 Spectrogram of mitral valvestenosis (atrial fibrillation) after noise reduction

在此,本文也对所提出的算法进行了对比,在同等条件下,分别使用LMS算法、维纳滤波算法以及EMD和改进的维纳滤波算法对心音信号进行处理,并将他们的信噪比(SNR)作为评判值.表1是它们的对比数据.

表1 3种算法降噪之后的信噪比Table 1 Signal-to-noise ratios after noise reduction by the three algorithms

从表1可直观的看出,优化的维纳滤波算法与LMS算法、传统的维纳滤波算法相比较,其信噪比明显提升,降噪效果明显.

对于降噪之后的数据,通过MFCC算法,提取出正常心音与降噪之后的二尖瓣狭窄(心房心颤)信号的特征值,并将其输入SVM中进行分类,分类结果如图6、图7所示.

结合图6、图7和表2可得,降噪之后的二尖瓣狭窄(心房心颤)信号可以更好地被分类.对于降噪二尖瓣狭窄(心房心颤)信号在SVM分类中其均方误差比含噪二尖瓣狭窄(心房心颤)信号低0.030 75,平方相关系数高0.038 51.可得出结论,此算法可适用于解决医学上心音信号的降噪问题.

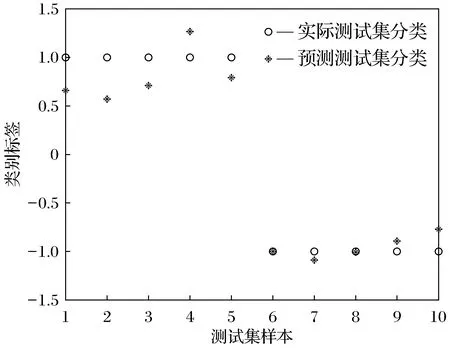
图6 含噪二尖瓣狭窄(心房心颤)心音与正常心音的分类结果Fig.6 Classification of noisy mitralstenosis (atrial fibrillation) heart sounds and normal heart sounds

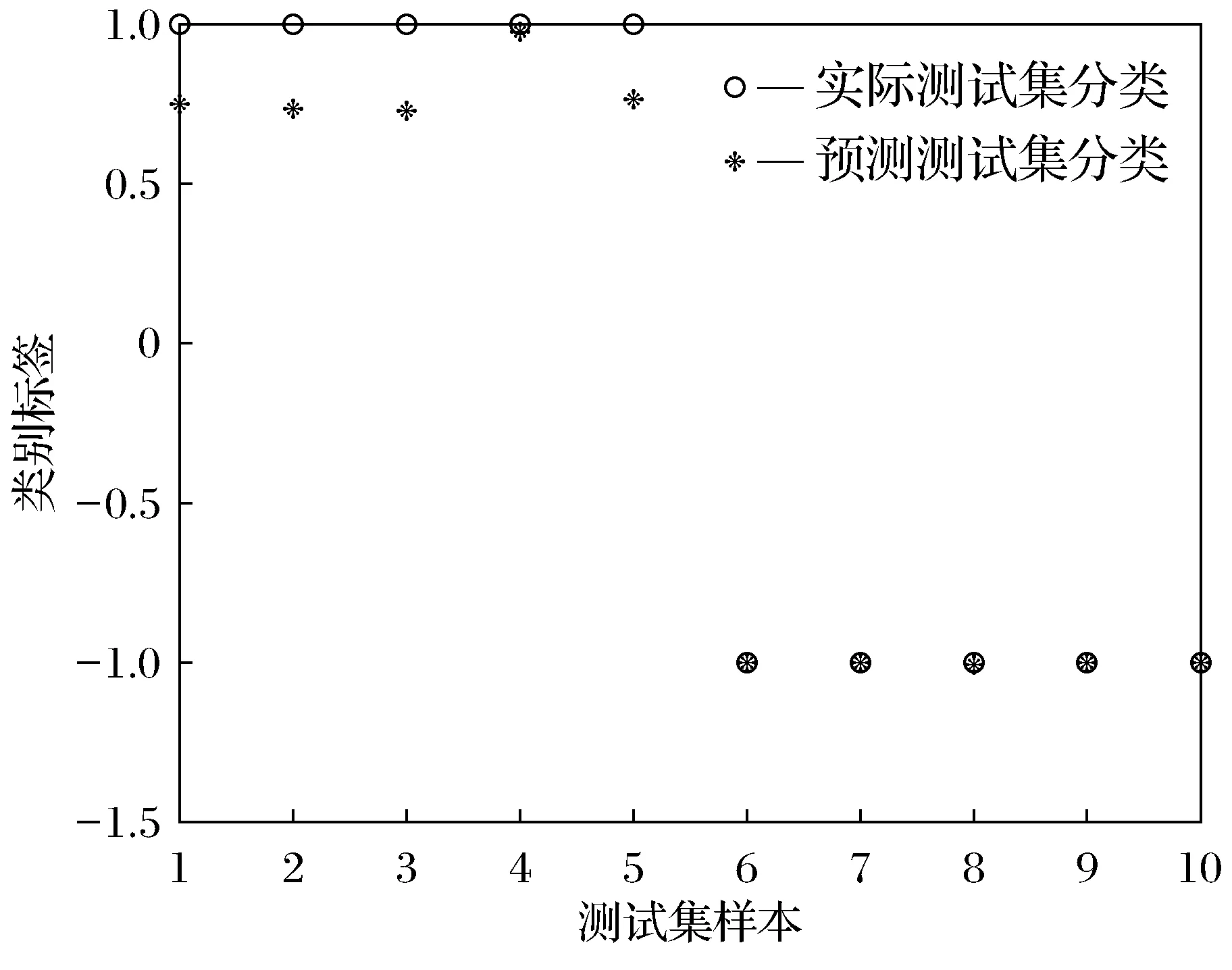
图7 降噪后二尖瓣狭窄(心房心颤)心音与正常心音的分类结果Fig.7 Classification of mitralstenosis (atrial fibrillation) heart sounds and normal heart sounds after noise reduction

表2 心音分类结果相关量Table 2 Heart sound classification correlation coefficient

5 结 语

本文在传统的维纳滤波算法上进行了优化,提出了优化的维纳滤波算法.此算法首先将实际的二尖瓣心音信号进行了降噪,减少了噪声的能量,再通过离散S变换的维纳滤波算法降低噪声中的虚假频率,减少噪声信号的残留,增强了二尖瓣心音信号的降噪效果,此方法可有利于二尖瓣心音信号的分类,对于解决医学上的心音降噪问题也将会有一定的用途.