语言环境下具有容忍区间的有差异双边匹配决策方法
(湖南工业大学 理学院,湖南 株洲 412007)
0 引言
D.S.Gale 等[1]在入学匹配问题和婚姻稳定性问题的基础上提出了“双边匹配”的概念,并提出了经典的Gale-Shapley 算法。之后,众多国内外学者对其进行了研究,并提出了较多具有针对性的双边匹配决策方法[2-11]。双边匹配具有广泛的实际应用背景,目前已在人岗双边匹配[12-14]、公私合作中政府项目与企业的双边匹配[15-16]和婚姻匹配[17-18]等方面得到较广泛的应用。双边匹配决策问题包含中介和两个有限的主体集,每个主体都对另一方主体给出评价信息,其目的是由中介匹配双方主体并最大限度地使主体匹配到满意的另一方主体。
针对主体给出的评价值为清晰数而期望值为区间数或离散区间数的无差异型双边匹配决策问题,文献[17-18]分别基于匹配度和前景理论给出了两种决策分析方法。值得指出的是,文献[17-18]认为,评价值落在期望区间内所对应的匹配度为1,而落在期望区间外所对应的匹配度为0,其实这是值得商榷的。事实上,许多现实的双边匹配决策问题不属于无差异的情形,而是有差异的,如对于效益型准则,应是越大越好,故大于期望区间的评价值所对应的匹配度应大于期望区间内的评价值所对应的匹配度;而对于成本型准则,则是越小越好,故小于期望区间的评价值所对应的匹配度应大于期望区间内的评价值所对应的匹配度,因而无差异区间型准则下的匹配度计算方法存在一定的局限性。另外,目前已有研究利用语言信息来定性表达主体对对方主体的评价,并进一步提出了双边匹配决策方法[19-22]。但针对双方主体给出的评价为语言信息而期望水平为区间语言信息的情形缺乏研究。基于此,本文拟考虑区间型准则的差异性,针对不同区间的评价值,分别定义相应的匹配度,并进一步提出一种双边匹配决策方法,最后应用婚姻匹配算例进行验证和分析。
1 预备知识
1.1 语言标度
语言标度由若干语言术语组成,能够比较准确地表达模糊信息。徐泽水[23]设定了语言标度,τ≥0,其中sφ表示语言术语,s-τ和sτ分别表示决策者实际使用的语言术语的下限和上限,且s满足
1)如果φ1>φ2,则>;
为较准确地描述主体的评价信息而又保证简便性,课题组设定τ=3,即采用7 粒度的语言标度S7={s-3,s-2,s-1,s0,s1,s2,s3},其中s-3表示“极差”,s-2表示“差”,s-1表示“较差”,s0表示“一般”,s1表示“较好”,s2表示“好”,s3表示“极好”。
定义1设为实数,若则称k为区间数,其中和分别表示k的左右端点。特别地,若=,则k退化为实数[17]。
定义2设,为语言术语集,τ≥0,若,sφ1≤sφf,则称s为离散语言区间术语,其中sφ1和sφf分别表示s的左右端点。特别地,若sφ1=sφf,则s退化为语言术语,记s为。
1.2 双边匹配
定义3设甲方主体集合为A={A1,A2,…,Am},m≥2,Ai表示甲方第i个主体,i=1,2,…,m;乙方主体集合为B={B1,B2,…,Bn},m≥n≥2,Bj表示乙方第j个主体,j=1,2,…,n。设γ:A∪B→A∪B为一一映射,若满足以下3 个条件,则γ为双边匹配[24]。
1)γ(Ai)∈B,
2)γ(Bj)∈A∪{Bj},
3)γ(Ai)=Bj当且仅当γ(Bj)=Ai。其中γ(Ai)=Bj表示Ai与Bj匹配并构成匹配对(Ai,Bj),γ(Bj)=Bj表示Bj无匹配对象,由于其匹配对(Bj,Bj)在匹配结果中无意义,故忽略。
2 双边匹配决策方法
2.1 问题描述
语言环境下具有容忍区间的双边匹配决策问题由以下几个部分构成。甲方主体的准则集合为,α≥2,准则对应权重为,即准则的权重为,0≤≤1,。乙方主体的准则集合为准则对应权重为,即准则的权重为,0≤≤1,。准则间相互独立,不互相产生影响。Bj在准则下对Ai的评价值为,构建评价值矩阵,Bj在准则下的容忍区间为;Ai在准则下对Bj的评价值为,构建评价值矩阵,在准则下的容忍区间为;所有的评价信息和容忍区间都由主体以语言的形式给出。本文要解决的问题是依据双方主体的语言评价信息、容忍区间和准则权重,如何通过有效的双边匹配决策,获得最优匹配方案。
2.2 匹配度
由于双边匹配决策问题中的准则主要分为效益型准则和成本型准则,所以此部分从效益型准则和成本型准则两个方面给出匹配度的计算公式。
效益型准则要求主体的评价值越高越好,在主体存在容忍区间的情况下,小于容忍区间的评价值对应的匹配度为0;容忍区间内的评价值对应的匹配度为0.5;大于容忍区间的评价值对应的匹配度为1。
若为效益型准则,对应的匹配度为

类似地,如果为效益型准则,对应的匹配度为

为Ai在准则下对Bj的评价值。
不同于效益型准则,成本型准则要求主体的评价值越低越好,在主体存在容忍区间的情况下,小于容忍区间的评价值对应的匹配度为1,容忍区间内的评价值对应的匹配度为0.5,大于容忍区间的评价值对应的匹配度为0。
如果为成本型准则,对应的匹配度为

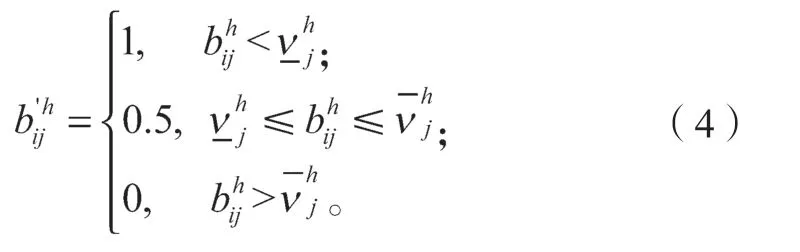
为Ai在准则下对Bj的评价值。
进一步利用线性加权集结算子将各准则下的匹配度集结为总匹配度:

式(5)(6)中:aij为Bj对Ai的总匹配度;
为对应的匹配度;
为准则的权重;
bij为Ai对Bj的总匹配度;
为对应的匹配度;
为准则的权重。
2.3 双边匹配模型
设xij为0,1变量,且在满意双边匹配中,由双方主体的总匹配度矩阵建立多目标优化模型(M-1):
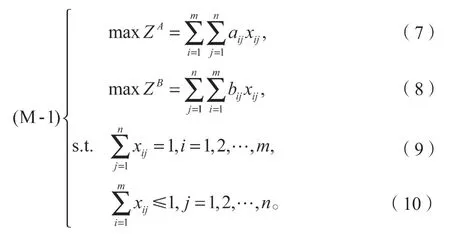
式(7)中maxZA表示乙方主体对甲方主体的总匹配度达到最大值;式(8)中maxZB表示甲方主体对乙方主体的总匹配度达到最大值;式(9)表示对于每一个甲方主体,都能找到一个乙方主体与之匹配,式(10)表示对于每一个乙方主体,可能不存在甲方主体与之匹配。
可采用线性加权法将多目标优化模型(M-1)转化为单目标优化模型。设甲方主体的权重为ωA,乙方主体的权重为ωB,且0≤ωA≤1,0≤ωB≤1,ωA+ωB=1,建立单目标优化模型(M-2):

式(11)中maxZ表示综合甲乙双方对对方主体的匹配度达到最大值。
模型(M-2)可使用支持线性优化的优化软件包进行求解,如Matlab、Lingo11。
定理1优化模型(M-2)存在最优解。
证明由于求解目标为0,1 变量,故可将模型(M-2)转化为指派问题,并用匈牙利算法求解。由模型可知,式(11)自变量数目为mn,故至多出现2mn个解。显然,匹配方案i=1,2,…,m;j=1,2,…,n,为目标函数的可行解,故模型(M-2)的可行域非空,则在该可行域中,必能在某处取值使得式(11)目标函数达到最大值,取得最优解,证毕。
综上,给出语言环境下主体存在容忍区间的有差异双边匹配决策方法的计算步骤:
步骤1利用式(1)~(4)计算各准则下评价值对应的匹配度。
步骤2利用式(5)~(6)将各准则下的匹配度集结为总匹配度并构建总匹配度矩阵和。
步骤3基于总匹配度矩阵建立多目标优化模型(M-1)。
步骤4将多目标优化模型(M-1)转化为单目标优化模型(M-2)。
步骤5求解单目标优化模型(M-2)得到最优匹配方案。
3 算例分析
株洲一婚介所对3 位女士(A1,A2,A3)和4 位男士(B1,B2,B3,B4)作婚姻匹配,双方共同考虑的准则有家境C1、年收入C2及相貌C3。其中C1、C2、C3的准则评价值均包含在7 粒度的语言标度S7,假设准则权重向量为W=(0.3,0.4,0.3)T,显然3 个准则都为效益型准则。由于甲方主体和乙方主体的准则集合相同,将和同时表示为,α=3。男士对女士给出的评价值矩阵和容忍区间如表1所示;女士对男士给出的评价值矩阵如表2所示,与RB相对应的容忍区间如表3所示。

表1 评价值矩阵RA 和相应容忍区间Table 1 Evaluation matrix RA with its related tolerance interval

表2 评价值矩阵RBTable 2 Evaluation matrix RB

表3 与RB 相对应的容忍区间Table 3 Tolerance interval related to RB
以下利用本文提出的双边匹配决策方法求解匹配结果。
步骤1利用式(1)和式(2)计算各准则下评价值对应的匹配度。各准则下男士对女士的评价值对应的匹配度和各准则下女士对男士的评价值对应的匹配度可分别由表4和表5表示。
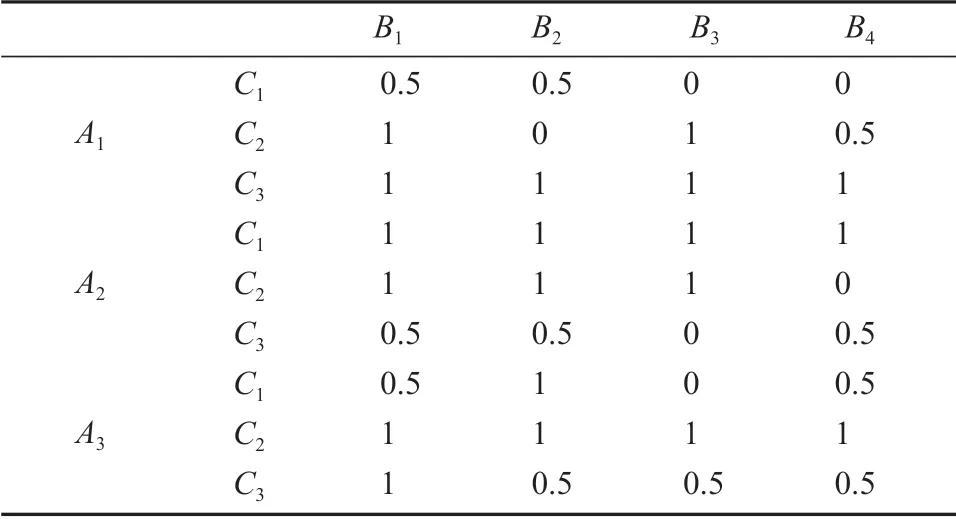
表4 各准则下男士对女士的评价值对应的匹配度Table 4 Matching degrees of evaluations of females given by males under each criteria
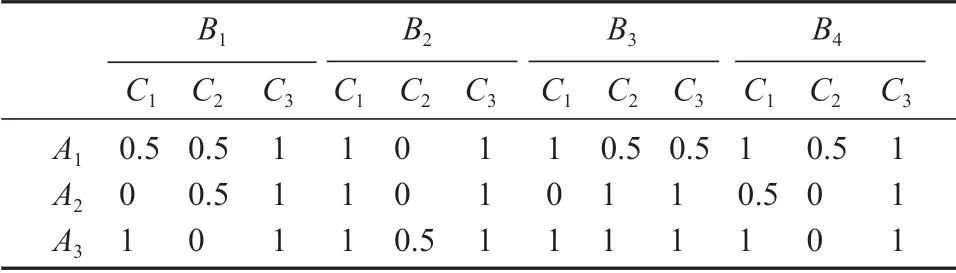
表5 各准则下女士对男士的评价值对应的匹配度Table 5 Matching degrees of evaluations of males given by females under each criteria
步骤2利用式(5)和式(6)将各准则下的匹配度集结为总匹配度。男士对女士的匹配度和女士对男士的匹配度可分别由表6和表7表示。
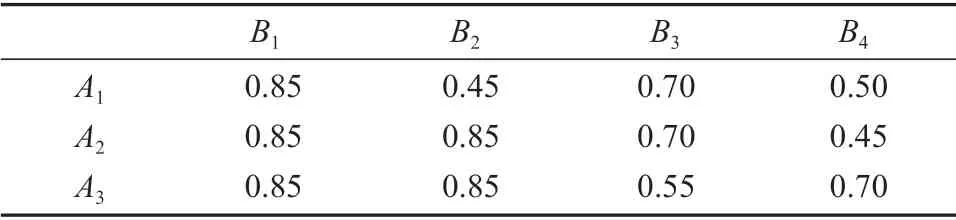
表6 男士对女士的匹配度Table 6 Matching degrees of females give by males

表7 女士对男士的匹配度Table 7 Matching degrees of males give by females
步骤3基于表6和表7所示数据建立多目标优化模型(M-1)。
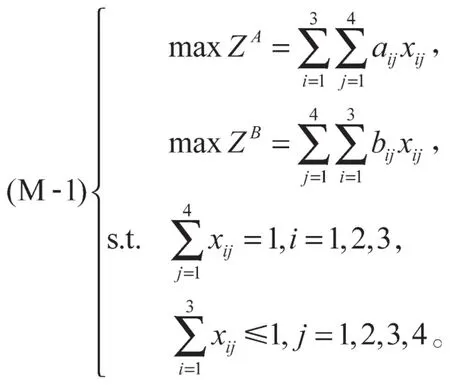
步骤4由于婚介所未给出对男方和女方的偏好信息,故ωA=ωB=0.5,将多目标优化模型(M-1)转化为单目标优化模型(M-2)。
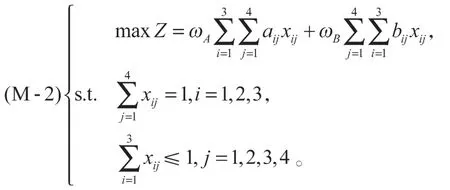
步骤5求解单目标优化模型(M-2)得到匹配结果x11=1,x23=1,x32=1,即最优匹配方案为{(A1,B1),(A2,B3),(A3,B2)},B4无匹配对象。
4 对比分析
文献[17]认为评价值对应的匹配度只能为0 或1,即期望区间内的评价值对应的匹配度为1 而期望区间外的评价值对应的匹配度为0,然而在考虑效益型准则和成本型准则后,本文指出:在效益型准则下,大于期望区间的评价值对应的匹配度应大于期望区间中的评价值对应的匹配度;在成本型准则下,小于期望区间的评价值对应的匹配度应大于期望区间中的评价值对应的匹配度。效益型准则下,文献[17]中主体给出的期望区间在本文中可视为容忍区间右端点至语言标度中最大语言术语的左开右闭区间,相对地,成本型准则下[17]中主体给出的期望区间在本文中可视为容忍区间左端点至语言标度中最小语言术语的左闭右开区间,故容忍区间将语言标度区分为了3 个有差异的区间,每个区间评价值对应的匹配度不同。为研究[17]提出的双边匹配决策方法与此研究所提出的双边匹配决策方法有何异同,假定在此研究的实例中,容忍区间中的评价值对应的匹配度为1,对应于文献[17]为期望区间中的评价值对应的匹配度为1,且双方主体的权重保持均等,则得到最优匹配方案{(A1,B3),(A2,B1),(A3,B2)},B4无匹配对象。
在匹配度修改处理后,A1的匹配对象由B1变为B3,A2的匹配对象由B3变为B1,不难发现,在表3和表4与A1,B3二者相关的匹配度中,匹配度0.5出现的次数较多,与A2,B1二者相关的匹配度中,匹配度0.5 出现的次数同样较多,在将匹配度0.5 修改为1 后,对(A1,B3)和(A2,B1)两组主体的匹配倾向起到了放大作用。虽然整体来看,在将匹配度0.5修改为1 后,对所有主体的匹配倾向都起到了放大作用,但是对(A1,B3)和(A2,B1)两组主体的匹配倾向的放大作用要高于其他任意两组主体的匹配倾向放大作用,这就导致了最优匹配结果的改变。
5 结语
无差异双边匹配决策方法利用期望区间将评价值信息总区间划分为两个具有不同匹配度的区间,本文指出该方法在效益型准则和成本型准则的情形下不适用,然后提出容忍区间,在语言环境下指出容忍区间内的评价值对应的匹配度为0.5,将语言标度划分为3 个不同的区间,分别针对3 个区间的评价值定义匹配度,体现不同区间中评价值的差异性。在容忍区间和匹配度的基础上,本文提出了一种有差异双边匹配决策方法。最后,本文将所提出的有差异双边匹配决策方法与无差异双边匹配决策方法进行了对比与分析,指出本文所提出的方法适用性更广泛。

