基于柯西色散公式测量费尔德常数的方法

叶昱成 梁小冲 蒋 昕

(四川大学物理学院,四川 成都 610200)

费尔德常数是晶体和溶液的特性常数之一,其主要应用于磁光效应之中。目前测量费尔德常数的主要方法有偏振激光测量法、解析谱法等。柯西色散公式是法国数学家柯西发现媒质的折射率与真空中入射光的波长的数学关系。由此可以提出一种在分光计实验平台上利用柯西色散原理测量费尔德常数的新方法[1-3],通过分光计测量汞灯发出的光线在三棱镜及三棱镜容器中发生色散时,每种特征谱线对应的折射率,进而计算出晶体的费尔德常数。此方法实验周期短,成本较低,可适应于多种环境下,使得测量更加简便[4]。

1 实验原理

1845年,M.Faraday 观察到,一束线偏振光在磁场的作用下,偏振光的振动面将发生旋转,旋转角ψ与样品长度D和磁感应强度B成正比,比例系数V称为费尔德常数[5],

费尔德常数与偏振光波长、材料性质和磁场方向有关,描述了特定材料的法拉第磁光效应的强度[6]。

1.1 费尔德常数与光波波长的关系推导

由波动光学中的结论[17]

其中,nL,nR分别为特征谱线中的左旋、右旋偏振光在材料中的折射率。

设介质中原子的轨道电子具有磁矩[16]

式中L为轨道角动量。

在磁场B中,一个电子磁矩有势能Ep为[7]

式中Laxis是电子轨道角动量的轴向分量。

当平面偏振光通过磁场B作用在折射率为n的样品介质上,光子使电子由基态激发到高能态。处于激发态的电子吸收光子的角动量,动能没有改变,而势能则增加ΔEp,其大小为[7]

上式中的正负号对应于左旋光和右旋光。

因为光子具有能量ħω,故样品介质对光的折射率n是ħω和ΔEp函数。左旋光量子的能量E为

同理,对右旋光量子有

忽略小量,将式(4)、式(5)代入式(2),得到

与式(1)比较得到

根据泰勒展开前柯西色散公式

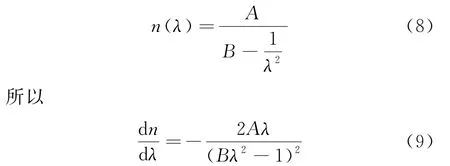
将式(9)代入式(7)中

1.2 费尔德常数的测量方法

在得到式(10)后,需要开始测定同一物质四个不同波长下的折射率n(λ),然后拟合出柯西色散公式并求出色散系数,进而求得待测物质的费尔德常数[8]。

如图1所示,汞灯光源发出的光以入射角i1入射到三棱镜的一个光学表面,经三棱镜折射后从三棱镜的另一个光学表面射出并发生色散,入射光和出射光之间的夹角称为偏向角δ。当棱镜顶角A′一定时,偏向角δ的大小随入射角i1的变化而变化。可以证明对同一种波长的光谱线,当i1=i4时,δ最小,这时的偏向角称为最小偏向角δmin[9-12]。当i1=i4时,由几何关系得出

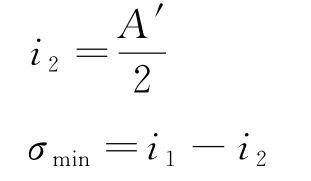
由上式解出

图1 棱镜色散

设棱镜材料对该波长的折射率为n,由折射定律sini1=nsini2可得

测得棱镜的顶角A′及最小偏向δmin后,即可由式(11)计算棱镜材料对不同波长的光谱线的折射率n[8-10]。

由实验所测得的不同特征谱线对应的折射角¯θ,可计算出偏转角δmin的大小

如图2所示,分光计光源发出的光经平行光管后成为平行光;平行光经载物台上的光学元件反射、折射或衍射后改变传播方向;绕中心转轴转动望远镜,先后接收未经过被测光学元件改变方向和经过被测光学元件改变方向后的平行光,由读数圆盘读出两种情况下望远镜所在位置的角度,即可由式(12)计算最小偏向角σmin,将计算结果代入式(8)计算出不同波长的谱线对应的折射率大小,利用此数据拟合出柯西色散公式中色散系数A、B 的数值大小,绘制出n-λ图像,并将拟合结果代入式(10)中计算出样品的费尔德常数大小[13]。

图2 普通分光计

1.3 液体费尔德常数的测量

对于液体费尔德常数的测量,我们使用一种三棱镜状容器来盛装液体,其测量光路如图3所示。

图3 溶液费尔德常数测量光路

图3以单色光入射为例,由于制作三棱镜杯子的材料折射率为n1=1.515,而一般溶液的折射率n2均小于此值,故考虑溶液折射率小于外侧玻璃的情况,当寻找到入射光在溶液中的最小偏向角时,光路如图3所示。由于此光路具有对称关系,可以得到入射角ia=ie,折射角ib=id,此时

而从图3中可以得到角度关系

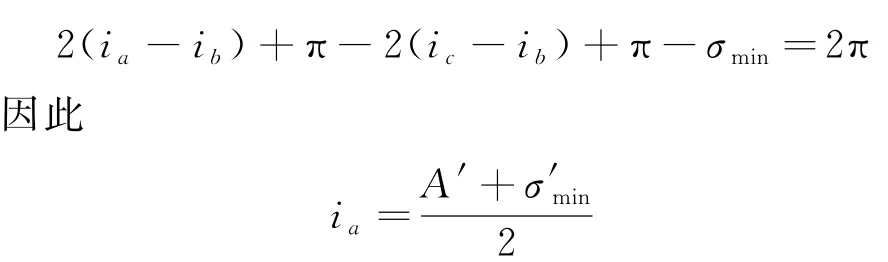
溶液费尔德常数的计算公式可表达为:

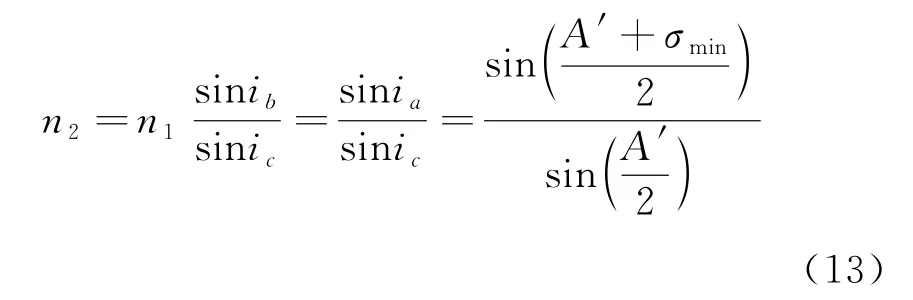
其中,σmin即为此时的最小偏向角。将式(13)得到的不同波长对应的折射率进行拟合计算,可拟合出柯西色散公式中的常数A、B,进而求出费尔德常数的大小。

2 实验方案及数据处理分析

2.1 实验方案

图4

(1) 利用十字叉丝对准白光(如图4(a)所示),读出此时入射光对应的角度θ0,将三棱镜或盛装液体的三棱镜容器的顶角置于载物台中心附近,先在出射光一侧找到出射光的大致位置,然后转动镜筒,从望远镜中找到汞灯的四条特征谱线(其顺为黄、绿、蓝、紫或紫、蓝、绿、黄)[15-17]

(2) 此时先顺时针调节载物台,使得特征谱线移动至最小偏向角的位置[13],然后转动目镜筒,使十字叉丝依次对准四条特征谱线(如图4(b)、(c)所示),并在读数圆盘上读出每种谱线对应的出射角θ′。

(3) 完成读数后,将载物台继续沿顺时针转过一定角度(5°以上),后将其沿逆时针转动至最小偏向角处,读出此时每种谱线对应的出射角θ″,上述顺时针和逆时针两次测量求均值方法的目的是减小最小偏向角的测量误差,并消除仪器的回空误差[5]。

将θ′和θ″求平均值得到的记录在下方四个表格中,其中表1、表2、表3、表4分别记录汞灯发出的白光在经过重火石晶体、水、浓度5%的葡萄糖溶液、浓度10%的葡萄糖溶液后,四种特征谱线对应的出射角。

表1 三棱镜晶体的四种特征谱线的出射角(θ0=57°57′)

表2 水的四种特征谱线的出射角(θ0=57°57′)

表3 浓度5%葡萄糖溶液四种特征谱线的出射角(θ0=57°57′)

表4 浓度10%葡萄糖溶液四种特征谱线的出射角(θ0=57°57′)

2.2 数据处理分析

其中对于三棱镜,

A=0.000222218,B=0.000153724

对于水,

A=0.000868629,B=0.000650003

对于浓度5%的葡萄糖溶液,

A=0.000841844,B=0.000628817

对于浓度10%的葡萄糖溶液,

A=0.000922218,B=0.000682626

取波长为四种光波长的平均值¯λ=473.2nm,并将¯λ,A,B代入式(10)中进行计算,得到三棱镜和水、浓度为5%、10%葡萄糖溶液的费尔德常数的测量值分别为

V三棱镜=898.31′·T-1·cm-1

V水=174.80′·T-1·cm-1

V5%的葡萄糖溶液=87.72′·T-1· cm-1

V10%的葡萄糖溶液=194.49′·T-1· cm-1.由于此分光计的测量精度为1′,因此测量出的费尔德常数实际精度为0.1′·T-1·cm-1。利用软件计算并绘制的不同波长的光在不同介质中的折射率,与其理论曲线进行对比,图5为三棱镜、纯水和浓度为5%,10%葡萄糖溶液中的柯西色散公式拟合结果。根据四种样品中的测量数据,可以利用Origin软件计算出测量结果的平均相对误差,在测量精度为0.1′·T-1·cm-1时,平均误差eR＜1.5%。对比钱小凌利用红光激光器精确测量费尔德常数得到的结果[14],本文提供的测量方法相对误差小于2%。然而,红光激光器精确测量费尔德常数的方法对环境温度、亮度等实验条件要求较高,因此不利于在一般实验室条件下展开。

3 结语

实验测量过程使用普通分光计,通过四条汞灯特征谱线拟合出柯西经验公式,测量出晶体和溶液费尔德常数,得到实验误差很小的结果,极大降低了实验成本,减少了实验周期,且自然光对本实验影响不大,故实验可在多种环境下开展。此实验中提供的方法不仅可以用于快速测定费尔德常数,也可在大学物理实验中进行拓展。