陀螺仪特斯拉计的相关讨论

姚 尧 李文华,2 王晓杰,2 王 槿,2 潘崇佩,2 文小青,2

(南开大学1物理科学学院;2基础物理国家级实验教学示范中心,天津 300071)

第32届青年物理学家锦标赛(International Youth Physicist's Tournament,IYPT)的第12道题目“Gyroscope Teslameter”内容为:A spinning gyroscope made from a conducting,but non-ferromagnetic material slows down when placed in a magnetic field.Investigate how the deceleration depends on relevant parameters。即研究一个非铁磁性导体在磁场中运动并减速的问题。题目中涉及的装置与电磁涡流制动[1-3]装置原理类似,对应于基础物理内容中的楞次定律和法拉第电磁感应定律知识点。特斯拉计涉及基础物理实验中磁场的测量。磁场的测量有很多方法,包括磁针法、电磁感应法、半导体(霍尔效应)探测法、核磁共振探测法、超导效应法、磁光效应法等[4]。

本文通过求解体系所满足的麦克斯韦方程,解释了影响其运动的相关因素,并用实验数据对其运动规律进行了验证和解释,最后并将此原理用于制造一个陀螺仪特斯拉计。

1 理论分析

1.1 背景原理

试想如图1(a)所示,当一个闭合线圈被恒力F牵引着远离磁场区域时,由法拉第定律[5]可知,线圈上会产生感应电动势ε:

其中ΦB为穿过线圈的磁通量,B为磁场的磁感应强度。如果线圈的速度为v,则

在线圈中同时会有感应电流i产生,此时导线在磁场中会受到安培力为

安培力的合力与其运动方向相反,此时外力F对系统所做的功一部分转化为线圈的动能,一部分转化为线圈中的焦耳热能。如果将闭合线圈换成一块普通导体板(图1(b)),有磁场覆盖区域的导体板可划分为并排放置的导线,其在远离磁场时会做切割磁感线运动,从而在导体板内形成闭合回路的路径上产生感应电流,但由于平板内电流没有固定导线形状的限制,会呈涡旋状存在。导体板的运动也会类似于闭合线圈在磁场中的情形,因受到安培力的作用运动受阻,从能量的角度考虑,在不考虑外力作用时,导体板的动能将全部转化为导体板内的焦耳热能。

图1 线圈和导体板切割磁感线

1.2 模型建立

图2 陀螺仪在磁场中的模型

对比导体板运动情况,一个旋转的陀螺仪在磁场中的运动可以被简化为一个导体圆盘在磁场中旋转的模型。整体可分为两种情况,一种是导体圆盘完全被磁场B=B(x,t)覆盖,如图2(a)所示,此时导体圆盘可被看做由沿半径方向排列的金属棒组成,由方程(2)可知,圆盘上会产生由圆心指向边缘的感应电动势,但是没有接通外部电路,并不会产生感生电流,因此也不会受到磁场的安培力作用,圆盘的运动不受磁场的影响。再有一种情况就是磁场B(x,t)部分覆盖导体圆盘(图2(b)),不同于前一种情况,导体在转动时,一部分在磁场中切割磁感线产生感应电动势,一部分在磁场外作为外接电阻,形成闭合电路,从而在导体中会产生感应电流。此时导体盘会受到与转动方向相反的安培力而减速直至停止,即在忽略外界摩擦等阻力的情况下导体圆盘的动能完全转化为导体盘中的焦耳热能。所以只有在导体圆盘部分处于磁场中时,才会因产生涡旋电流而使动能转化为焦耳热直至停止转动。

进一步简化模型,将磁场等效为导体圆盘上方固定一圆形永久磁铁,如图3所示,在此基础上建立两套右手坐标系(1)永磁铁所在固定坐标系:x,y,z;(2)旋转导体盘所在动坐标系:x′,y′,z′。

图3 导体圆盘和永久磁体位置关系侧视图

如图3所示,永磁体半径为R,置于半径为a的非铁磁导体圆盘上方b处,两个物体的中心轴线距离为d,导体圆盘的厚度为δ,电导率σ为有限值(即非超导体),且在本文讨论范围内δ≪a,0＜R≤a/2,R≤d≤a-R。首先考虑导体圆盘相

导体切割磁感线只需考虑以下情况

由导体坐标系到磁铁坐标系存在

其中u为导体圆盘的平动速度,由式(5)、式(6)可以得到

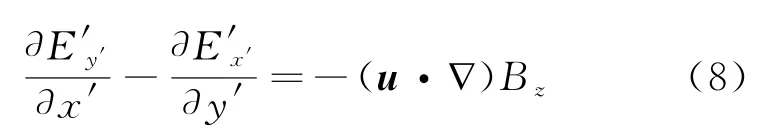
在导体坐标系中定义一个广义函数D′,并且其与导体的表面电流K存在如下关系

则由方程(8)可以得到

再回到磁铁的坐标系,在柱坐标系下由方程(10)可得

为求解方程(11)引入磁矢量势A,且

其中μr=1,j=jz(x,y)z为体电流密度。只有在r=R且表面极薄的一层才不为零,同样jz也被限制在厚度远小于R的范围内,因此由式(11)和式(12)可得

进而可以得到由矢量势Az所在场强的单位长度的自由能W和注入到导体盘上的功率P存在如下关系

当考虑导体圆盘绕固定轴以角速度ω旋转切割磁感线时,建立如图4所示的坐标关系,则存在

图4 导体圆盘绕定轴旋转时的坐标关系

此时对方程(12)和方程(13)进行求解可以得到

通过式(16)以及阻力矩满足的能量关系Tb=P/ω可以得到导体圆盘受到磁场的阻止力矩为

由式(21)可以看出在其他量固定的情况下,导体盘受到的电磁制动力矩与圆盘转动速度ω正相关,即圆盘的转速越大,所受的电磁制动力矩越大,随着制动力矩的作用,转速减小,制动力矩随着减小,直至导体圆盘停止转动。在固定初始转速ω和其他参量时,改变永磁体与导体圆盘中心的距离d,电磁制动力矩会存在一个极大值Tbmax。

在不考虑导体圆盘转动减速时存在的内摩擦力矩时,其所受到的总制动力矩为

I为导体圆盘的转动惯量。

2 实验验证与讨论

2.1 实验装置

我们按着图3所示的简化模型,对导体圆盘在磁场中的运动情况进行了相关实验验证。实验中所用装置如图5所示,其中导体圆盘装置采用市场上购买的简易单轴陀螺仪,圆盘材质为黄铜,电导率取σ=5.7×107S/m[7],厚度δ=0.769cm,半径a=2.45cm,质量m=133.45g,经固定后,黄铜圆盘可绕竖直的中心轴自由旋转。所用永磁体直径 为2R=0.95cm,厚度h=0.48cm。利用高斯计(HC803)对磁场进行测量。采用高速相机(Photron FASTCAM Mini UX50,2000fps)对导体圆盘的运动进行拍摄。

图5 实验装置图

2.2 实验结果与讨论

2.2.1 内摩擦力矩修正

实验中观测到如果给定陀螺仪一个初始转速,在无外界磁场时,转速也会减慢,需考虑陀螺仪内摩擦力矩的作用。在无外磁场时,式(22)可以表示为

由参考文献[8]可知,对于定轴转动体系,在转动过程中所受的阻力矩主要来自于转轴轴承处的摩擦力矩和体系所受到的空气阻力矩,且二者均与角速度ω有关,即Tf=Tf(ω)。考虑到本实验中所用单轴陀螺仪的结构简单且几何尺寸较小,故将Tf在较短时间内近似作为常量处理,则对式(23)两边积分可得

实验中,我们先移去永磁体,直接测量导体圆盘的自然减速过程,得到如图6所示的转速ω的衰减数据。

图6 内摩擦力矩作用下的转速衰减

导体圆盘的转动惯量I=ma2=4.005×10-5kg·m2,由转速衰减的实验数据拟合得到衰减系数为1.136rad/s2,可得陀螺仪的内摩擦力矩Tf=4.55×10-5N·m。

考虑了内摩擦力矩之后,在有外界磁场时,式(22)可以表示为

解此方程可以得到

其中

2.2.2 磁场的修正

当我们使用特斯拉计测量图4中圆形阴影区域内的磁场时,发现磁感应强度在中心部分近似保持均匀,随着距离中心O越来越远,磁感应强度的衰减越明显。由磁偶极子的磁感应强度衰减规律[6]以及实际测量中所用特斯拉计探头的大小(2～3mm),我们以图7所示磁场分布对导体圆盘上的磁场进行修正。即当距圆心O的距离r≤r0时,B=B0,当距中心距离r＞r0时,B(r)∝B0/r3,r0=1.5mm。对z向磁场进行修正后,式(27)变为:

图7 磁场衰减示意图

2.2.3 实验探究

由前面的讨论可知,导体圆盘在磁场制动力矩和内摩擦力矩的共同作用下,转速变化遵循指数衰减规律,衰减的快慢完全由式(26)指数项系数k来决定,此时内摩擦力矩项可视为常数项,则导体圆盘转速的变化可简化为

其中衰减系数β=k/I。由式(28)可知,k与导体圆盘和永磁体轴心间距离d近似成二次方关系,其反映磁场制动力矩Tb与d间的变化关系,衰减系数β亦遵循此规律。

实验上通过固定永磁体与导体圆盘间的竖直距离b,测得导体圆盘表面磁场区域中心处磁场大小为Bz0=0.13T,来探究导体圆盘的转速ω以及衰减系数β随着d的变化规律。在尽量保证初始转速一致的情况下,得到d=0.88,1.00,1.25,1.60,1.75cm 时,导体圆盘的转速变化数据如图8所示。

图8 永磁体和导体圆盘中心距离d 变化时圆盘转速变化情况

利用式(29)对图8中实验数据进行拟合得到衰减系数β随着轴心距离d的变化关系如图9所示,其中灰色实线为由式(28)得到的理论曲线。可以看到所得实验数据与理论预期变化趋势一致,但在轴心距离d较小和较大时数据有较大偏差。我们推测可能是导体圆盘的质心不在轴心,导致其实际转动惯量I大于理论的ma2/2,使得实际的衰减系数β=k/I会小于理论计算值。而在d较小时,由于其初始转速较小,且磁场作用的阻尼衰减作用比d较大时小,此时重力矩作用比较明显,使得实际衰减系数偏大。

图9 导体圆盘转速的衰减系数β 随轴心距离d 的变化实验数据与理论值对比

由式(27)可知,当外界磁场Bz已知时,在特定的位置d处,理论上可以预测导体圆盘转速的衰减速率。反之,当外界磁场未知时,可根据圆盘转速的衰减速率来反推磁场的大小,从而可以得到一个“陀螺仪特斯拉计”。即存在

其中I为导体圆盘的转动惯量,C为与导体圆盘材质和尺寸、永磁体尺寸以及两者轴心间距离相关的量为:C=利用此原理,我们固定d=1.45cm,利用式(30)得到此时由衰减系数反推磁场大小的理论曲线(图10中灰色实线所示),与用特斯拉计测量得到的磁场大小进行对比,结果如图10所示。实验数据与理论预期有较好的一致性。

图10 由衰减系数推算得到的磁场强度Bz0

3 结语

本文对第32届IYPT 赛题中第12 题“陀螺仪特斯拉计”进行了探究。通过理论分析将磁场中陀螺仪的减速问题简化为导体圆盘在磁场中的减速,并对模型的麦克斯韦方程进行了求解,通过解体系的常微分方程得到导体圆盘受到的电磁制动力矩及角速度变化,并对方程的解进行了内摩擦力矩和磁场的修正。通过改变轴心距离d,实验测得导体圆盘的转速衰减系数,并同理论进行比较。最后利用磁场大小与转速衰减系数间的对应关系将装置作为“陀螺仪特斯拉计”对永磁体的磁场进行了测量,实验结果与理论符合的较好。