理想气体比热容计算公式的对比研究
苑伟民,杨文川,廖天昊,马一歌
1.国家管网集团北海液化天然气有限责任公司,广西北海536000
2.中国石油工程建设有限公司西南分公司,四川成都610041
3.国家管网西南管道公司,四川成都610094
4.重庆科技学院石油与天然气工程学院,重庆401331
理想气体的比热容本身只是温度函数,但函数的形式目前在理论上尚无法求出,一般均为根据实验数据归纳的经验公式,如国内外文献中对理想气体比热容的估算均采用由测试数据通过回归得到的多项式,形式有所差别。由于理想气体焓和熵的计算公式是由理想气体定压比热容经积分而来,因此理想气体焓和熵计算公式的计算准确性取决于理想气体定压比热容。理想气体的比热容、焓、熵值是构成实际气体比热容、焓、熵值的一部分,其计算准确性将决定实际气体比热容、焓、熵计算的准确性。因此,理想气体的比热容、焓、熵计算的准确性对于实际气体比热容、焓、熵值计算的重要性是不言而喻的。文献[1-10]计算理想气体比热容的公式大多采用API 技术数据手册中的公式及其数据,经过单位转换进行引用。就目前国内文献来看,对ISO 20765-1 中公式使用较少。本文分析具有代表性的三个权威的理想气体比热容计算公式,给出了建议。
1 实际气体与其理想气体比热容的关系
根据热力学定义,实际气体与理想气体比热容之间的关系式为[9]:



2 HYSYS 计算公式


表1 HYSYS 理想气体比热容方程中的计算系数
质量比热容与摩尔比热容之间的转化关系为:摩尔比热容=质量比热容×摩尔质量。
3 API技术数据手册
API 技术数据手册截止到2016 年已经出版了10 个版本,多数文献中计算理想气体焓、熵、比热容的公式和数据都来源于该手册,计算系数不同的原因是进行了单位换算。随着版本的更新,计算理想气体焓、熵、比热容的公式并未发生改变,但计算系数发生了变化,适用温度范围也扩展了不少,但是并非使用的温度范围越大就越好,可能会带来准确度的问题。
理想气体定压比热容的计算公式:

式中:k2为单位换算系数,取4.187 020;B、C、D、E、F 为计算系数,取值见表2。
1976 年版(即第3 版) API Technical Data Book-Petroleum Refining[2]中关于理想气体比热容精度说明:在适用温度范围内热容误差在1.5%以内。但是超过适用温度范围时,误差可能很大。计算系数见1976 版API 技术数据手册。1992—2016 年版本的计算系数发生了改变,主要是为了拓宽温度的适用范围,但总体精度变差。其精度说明:比热容误差在5%以内。超过适用温度范围时,误差可能很大。

表2 1992—2016 版API 技术数据手册理想气体焓、熵在基准1 下计算系数[2]
4 ISO 20765-1中计算公式
GB/T 30491.1—2014 为 采 标 ISO 20765-1:2005[11-12],为简单表示,将标准中比热容计算公式改写如下[13-19]:


式中:B、C、D、E、F、G、H、I、J 为转换系数;R为通用摩尔气体常数,取8.314 51 kJ/(kmol·K);M 为组分i 的摩尔质量,kg/kmol。上述有关计算系数见表3。
根据该公式的引用文献说明,其计算精度和适用温度范围如表4 所示[16]。
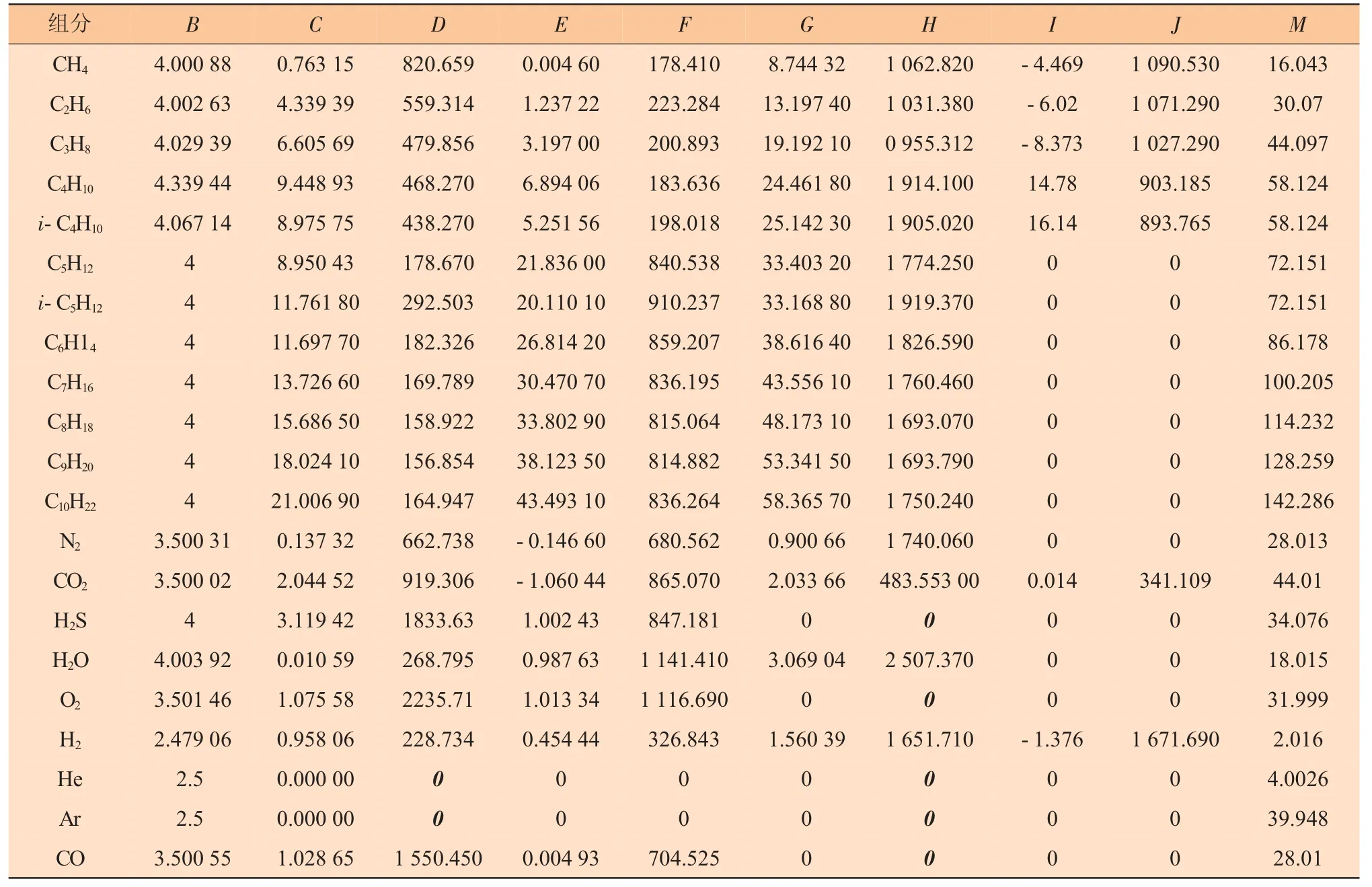
表3 ISO 20765-1:2005 中计算系数
表4 计算准确度说明
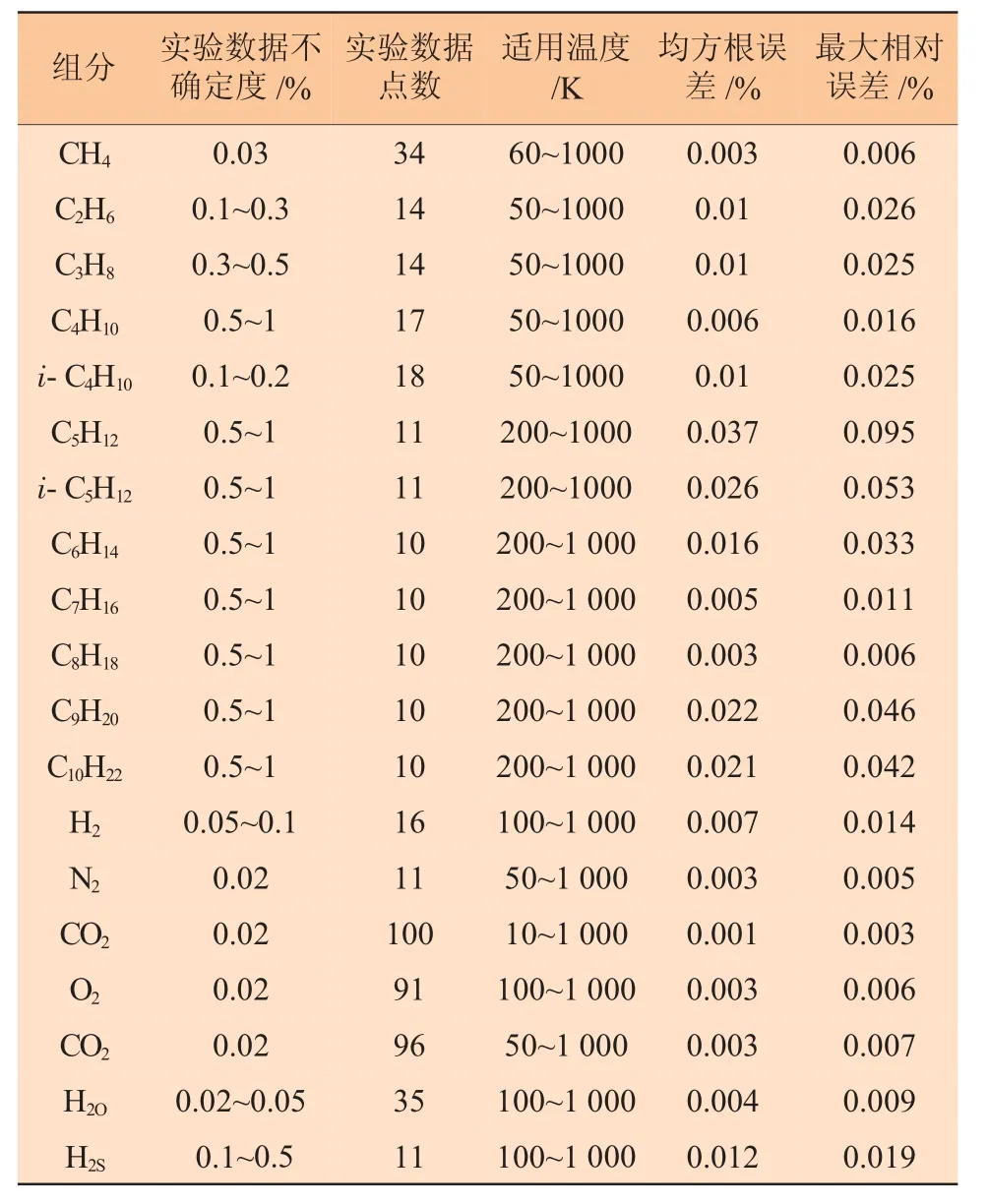
表4 计算准确度说明
实验数据点数CH4 0.03 34 C2H6 0.1~0.3 14 C3H8 0.3~0.5 14 C4H10 0.5~1 17 i-C4H10 0.1~0.2 18 C5H12 0.5~1 11 i-C5H12 0.5~1 11 C6H14 0.5~1 10 C7H16 0.5~1 10 C8H18 0.5~1 10 C9H20 0.5~1 10 C10H22 0.5~1 10 H2 0.05~0.1 16 N2 0.02 11 CO2 0.02 100 O2 0.02 91 CO2 0.02 96 H2O 0.02~0.05 35 H2S 0.1~0.5 11组分 实验数据不确定度/%适用温度/K 60~1000 50~1000 50~1000 50~1000 50~1000 200~1000 200~1000 200~1 000 200~1 000 200~1 000 200~1 000 200~1 000 100~1 000 50~1 000 10~1 000 100~1 000 50~1 000 100~1 000 100~1 000均方根误差/%0.003 0.01 0.01 0.006 0.01 0.037 0.026 0.016 0.005 0.003 0.022 0.021 0.007 0.003 0.001 0.003 0.003 0.004 0.012最大相对误差/%0.006 0.026 0.025 0.016 0.025 0.095 0.053 0.033 0.011 0.006 0.046 0.042 0.014 0.005 0.003 0.006 0.007 0.009 0.019
5 各方法计算准确性比较
以甲烷为例,利用ISO 20765-1、《API 技术数据手册》(1976 年版本)、《API 技术数据手册》(1992 年版本)、HYSYSV10 版本计算60 ~1 500 K,180 ~380 K 下的理想气体比热容,以McDowell 和Kruse[18]的实验数据为基准,进行相对误差比较计算,如图1、图2 所示。
6 结论及建议
经过对理想气体比热容的计算分析,得出以下结论和建议:
(1) HYSYS 和《API 技术数据手册》 属于同一类型的计算公式,相比较ISO 201765-1 而言,使用起来较为简单。
(2) 计算准确性从高到低的顺序依次为:ISO 20765-1、《API 技术数据手册》(1976 版)、 《API技术数据手册》(1992—2016 版)。

图1 60 ~1 500 K 下甲烷的理想气体比热容
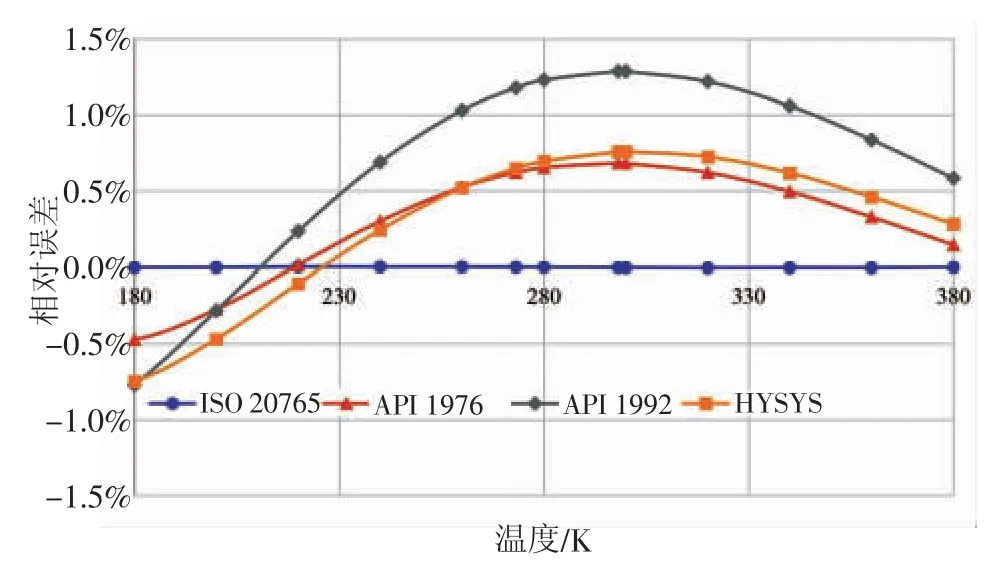
图2 180 ~380 K 下甲烷的理想气体比热容
(3) 《API 技术数据手册》(1976 年版本)和其以后的版本相比,1976 年之后的版本适用范围较宽,其计算准确度随着范围的扩大而减小,但是在适用温度范围内的总体准确度降低,在选取计算方法时应予注意。
(4) GB/T 30491.1 是翻译等同采用ISO 20765-1,但没有相应的标准解释文件和相应的计算软件,不利于推广。建议GB/T 30491.1 编写组对内容进行进一步完善,更易于理解和使用。
(5) 建议使用基于EXCEL 表格的计算方法进行理想气体比热容的计算,该方法简单易用,计算混合理想气体的比热计算效率高,并且可以通过EXCEL 给其他软件提供数据接口。

