地震动力作用对土质边坡稳定性的数值模拟分析研究

王 旭

(黑龙江省庆达水利水电工程有限公司，哈尔滨 150080)

1 绪 论

在影响土质边坡稳定性因素中，地震荷载是产生地震滑坡等现象的主要因素，通常地震荷载带来边坡的地震惯性力，降低整体边坡的稳定系数，下滑力加大导致出现边坡失稳。地震动力响应分析主要研究地震动荷载引起边坡的位移、应力、速度、加速度等量值的变化[1]。FLAC3D有限元分析软件基于强度折减法原理，研究边坡破坏的机理机制，可深入掌握动荷载作用下的边坡稳定性和失稳原理，进而有效提升加固措施保证边坡安全。

2 动力有限元分析原理

FLAC3D模拟三维岩土体在不同载荷作用下的非线性响应，步骤主要包括如下：①计算自重荷载下的初始应力；②选取动力分析模块，进行动力分析计算[2]。

动力荷载输入方式：加速度时程，速度时程，应力时程和集中力时程。动力荷载主要表现形式：①FISH函数。②TABLE命令定义的表。影响波传播的数值精度主要有岩土体的波速特性和输入波的频率成分。

边界条件定义，弹性波在岩土体边界处会产生反射，造成计算结果出现较大误差，本程序拟采用静态边界和自由场边界结合的方式来解决。

3 工程实例

3.1 模型建立

某边坡模型高10m，坡率1∶0.5， 坡脚63°，地质构造是水平层状结构，分为两层，上层Q4黄土，高度地面下4m，下层Q3黄土，均匀土体厚度10m。边坡设为弹塑性材料，土体模型采用实体(zone)单元模拟[3]。边坡岩体物理力学参数如表1所示，原始边坡网格划分如图1所示。

表1 边坡物理力学参数

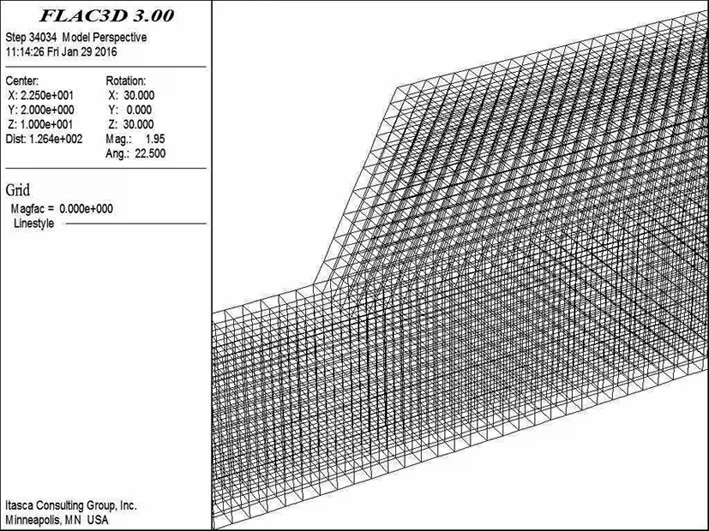
图1 边坡有限元网格剖分图

边界条件：上部为自由边界，不受约束；左右两侧水平约束；下部固定，法向约束，阻尼比0.142[4]。

3.2 地震波输入

该区基本设防烈度6度，文章选取地震波加速度为0.05g，波持续时间21.40s[5]。地震波加速度如图2所示。

图2 地震波加速度

3.3 计算结果

关键点布置情况如图3所示。通过数值计算，提取坡顶关键点a、斜坡面上关键点b、滑动区域内关键点c和d、相对不滑动区域关键点e和f的位移、速度、加速度时程曲线，关键点的水平、竖向位移如图4-图6所示。

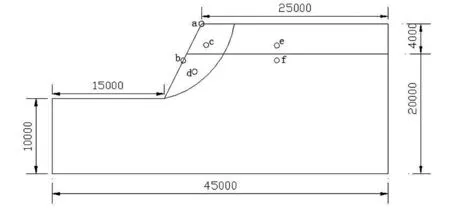
图3 关键点布置图

图4 关键点水平位移时程曲线

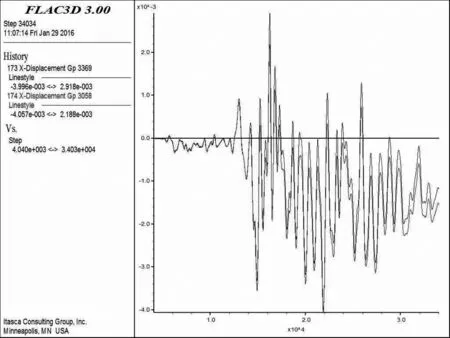
图5 滑动区关键点水平位移时程曲线

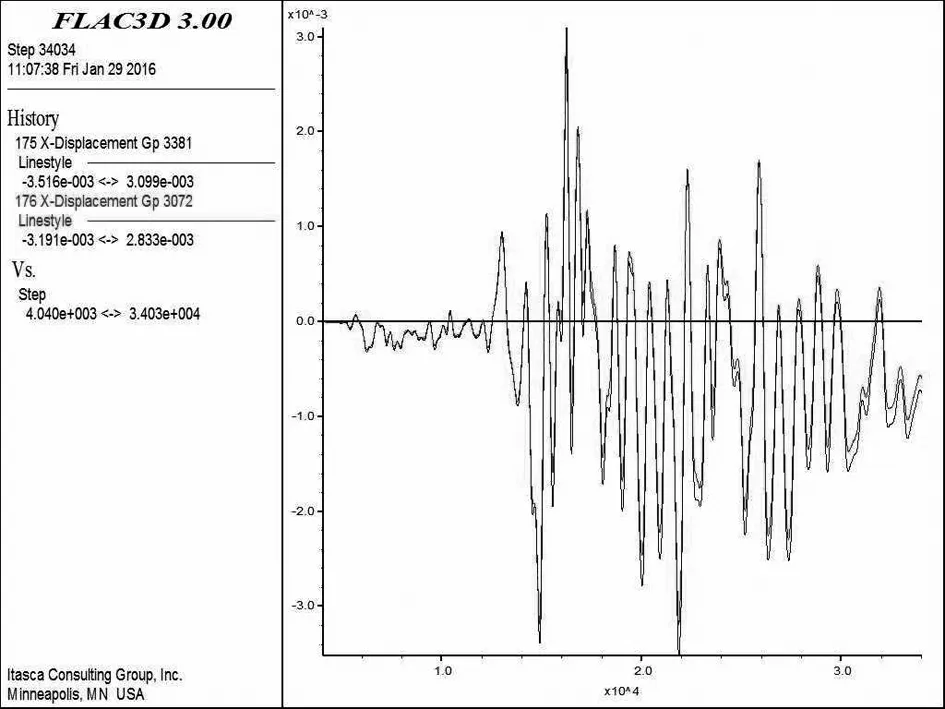
图6 非滑动区关键点水平位移时程曲线

由上图可以看出，地震荷载施加后关键点的水平、竖向位移最终趋于水平，数值收敛，没有发生突变，表明边坡保持稳定，该边坡在地震烈度小于设计烈度时，具有良好的抗震效果。

关键点的速度时程如图7-图9所示。

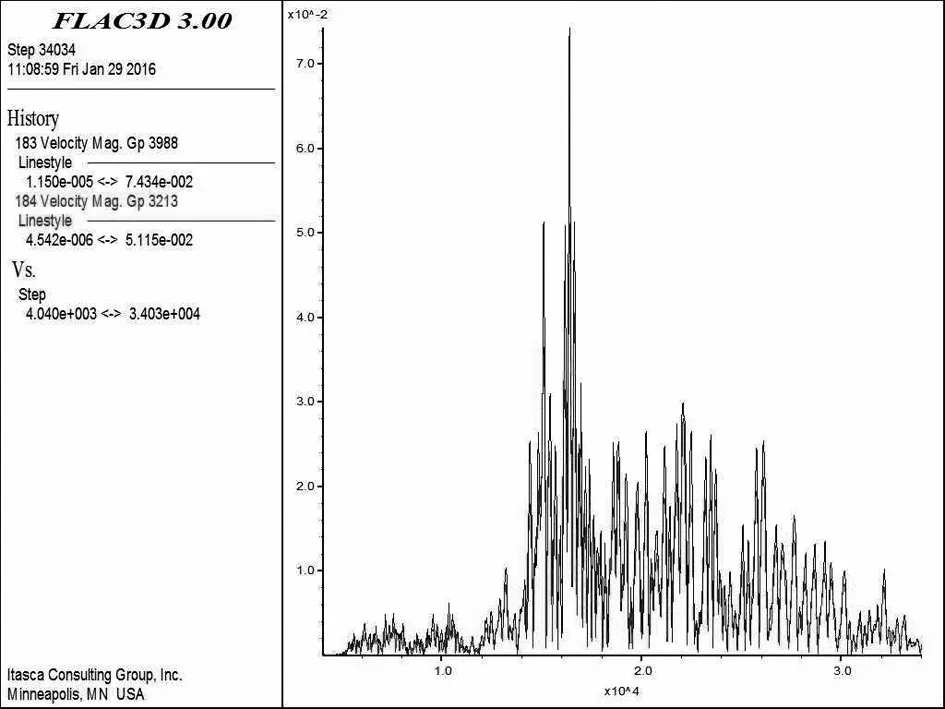
图7 坡顶和坡面上关键点速度时程图

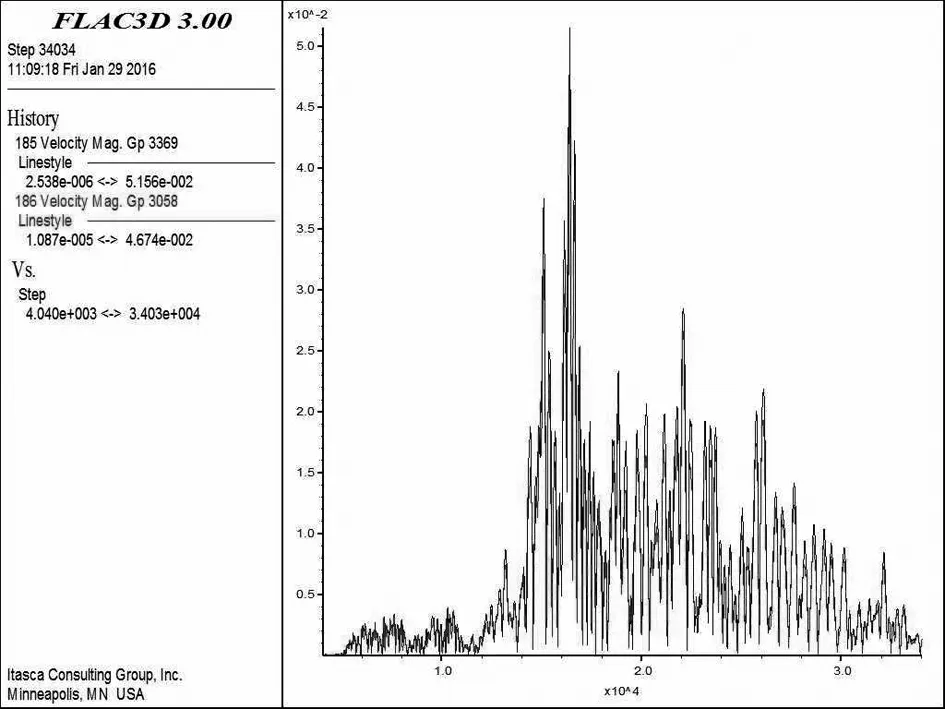
图8 滑动区关键点速度时程图

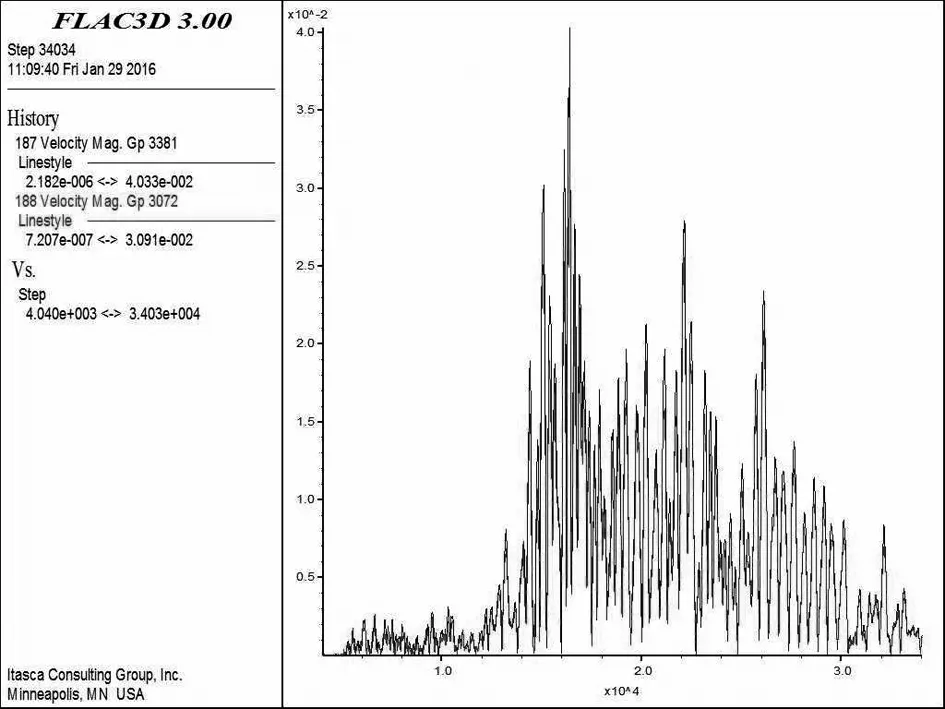
图9 相对不滑动区关键点速度时程图

由图可以看出质点速度大小为：坡顶>坡面>滑动区>相对不滑动区。在地震荷载施加后关键点的速度呈上下波动现象，随着荷载作用结束关键点速度最终为零，速度数值收敛，未发生突变，表明边坡保持稳定，该边坡在地震烈度小于设计烈度时，有良好的抗震效果。

关键点的水平、竖向加速度时程如图10-图11所示：

图10 关键点水平加速度时程图

图11 滑动区关键点水平加速度时程图

由图可知，随着地震荷载作用，坡顶、斜坡面上、滑动区域、相对不滑动区内关键点加速度时程变化均上下振动，最终趋于零。坡顶、斜坡面上和滑动区域内关键点的加速度明显大于相对不滑动区域，随着边坡不断增高，关键点加速度峰值越大，地震加速度作用愈显著，水平方向加速度的放大效果明显大于竖直方向。

4 结 论

文章基于有限元动力分析原理，建立地震作用下的边坡分析模型，计算分析地震结束时刻边坡的水平和竖向位移、边坡上关键点的位移、速度、加速度时程变化，研究设计地震力作用下边坡的动力响应问题。结果表明地震结束时坡顶和土层分界处发生较大的位移，有小部分的滑动但未贯通整个边坡，说明边坡是安全稳定的。