基于Sobol法的复合材料加筋板结构参数灵敏度

殷俊清, 赵诚诚, 陈永当, 程云飞, 顾金芋

(西安工程大学机电工程学院， 西安 710048)

复合材料加筋板结构广泛应用于飞机的机翼、尾翼的翼面等部位[1]，其在服役过程中经常受拉伸、弯曲、剪切等外载荷作用而产生屈曲变形，并发生局部失稳，此时仍具有较强的后屈曲承载能力[2-3]。设计合理的复合材料加筋壁板结构可以显著提高其可靠性、稳定性及承载能力。安全系数法是复合材料结构设计的经典方法之一，但由于缺少对随机变量的定量分析，导致该方法不能准确反映出结构的安全程度[4-5]。复合材料结构中的几何参数、材料属性以及加工工艺参数等均存在不确定性，这些变量的不确定性对结构可靠性的影响不可忽略[6-7]。因此，对包含大量参数的复合材料加筋板进行可靠性优化设计时，需要研究各随机因素对复合材料性能的影响程度。

目前，众多研究学者结合数值分析、仿真模拟及实验研究等手段，分析了随机因素对复合材料性能的灵敏度。王佩艳等[8]分析了个各设计变量对目标响应值的灵敏度，在此基础上，对复合材料加筋板结构进行了优化设计。Liu等[9]用总刚度矩阵和质量矩阵及其一阶导数描述了静力响应、特征值和特征向量的分析灵敏度分析方法，对复合材料层合板和壳体进行了灵敏度分析。Omairey等[10]研究了微观尺度的几何参数和材料性能不确定性对纤维增强复合材料的弹性和可靠性的影响及随机参数的灵敏度。阮文斌等[11]对复合材料结构输出位移和强度比的不确定性来源进行分析,得到输入变量的全局灵敏度排序结果。

全局灵敏度分析方法可以定量分析出单个变量或多个变量相互作用对输出响应的贡献程度，并且具有全局性和稳定性，广泛应用于可靠性分析、结构设计与优化等多个领域[12-14]。在复合材料不确定性分析方面，一些学者利用灵敏度分析法已经开展了探索性的研究，证明了该方法在复合材料结构分析方面的可行性[15]。现以复合材料加筋板为研究对象，选取屈曲载荷作为输出响应值，以复合材料加筋板的材料属性和几何参数作为设计变量，基于Kriging方法的代理模型建立加筋板输出响应与设计变量的函数关系，采用Sobol法求解复合材料加筋板材料属性和几何参数的灵敏度，研究结果可对复合材料加筋板可靠性设计提供指导。

1 复合材料加筋板的仿真分析

采用T形复合材料加筋板模型，如图1所示，其中：长La=280 mm、宽Wa=160 mm、筋条间距Sa=100 mm、翼板宽度W=24 mm、腹板高度H=20 mm。

复合材料加筋板材料属性如表1所示，蒙皮和筋条的铺层分别为[0/90/±45]s和 [0/90/45/0/-45]s，蒙皮的总厚度为1 mm，加强筋的总厚度为1.25 mm。

基于ABAQUS软件建立复合材料加筋壁板的仿真分析模型，为提高计算效率，模型中筋条和蒙皮均采用S4R单元进行建模，边界条件：加载一端开放施加载荷方向自由度，另一端固定，侧边开放自由度，采用Buckle计算模块对有限元模型进行特征值屈曲分析，其中第一阶模态如图2所示。

图1 复合材料加筋板模型示意图Fig.1 Schematic diagram of the composite reinforced plate model

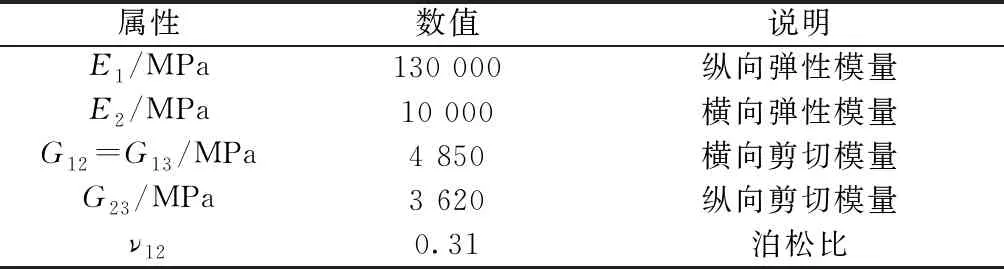
表1 材料属性Table 1 Material properties

图2 T形复合材料加筋板的一阶屈曲模态Fig.2 First-order flexion mode of T-shaped composite reinforced plates

通过仿真分析可得，T形复合材料加筋板的屈曲载荷为4.97 kN，与文献[16]实验数据4.89 kN相比，数值模拟数值与实验数值误差为1.6%，由此说明，研究模型是合理、准确的。

2 复合材料加筋板参数的灵敏度分析

基于有限元分析理论，在边界条件确定时，复合材料加筋板的屈曲载荷可以表示成材料属性和几何参数的函数[17]为

Pcr=f1(E1,E2,G12,G13,G23,T,θ,W,H)

(1)

式(1)中：Pcr为复合材料加筋板屈曲载荷；T为复合材料单层板厚度；θ为纤维±45°的铺层角度；W为翼板宽度；H为腹板高度。

由式(1)可知，Pcr的变化是由E1、E2、G12、G13、G23、T、θ、W、H改变引起的，为了有效地描述Pcr的变化，E1、E2、G12、G13、G23、T、θ、W、H均为随机变量。复合材料加筋板中变量分布[17]如表2所示。

表2 变量分布Table 2 Distribution of variables

由于复合材料结构的复杂性，等参数与屈曲载荷之间存在着隐函数关系。在求解复合材料加筋板参数灵敏度时，需多次通过ABAQUS软件进行数值模拟来计算屈曲载荷的数值。因此，进行复合材料加筋板参数灵敏度分析时就需要对屈曲载荷与多个参数之间的函数进行拟合。Kriging模型作为线性回归的一种改进技术，包含了线性回归部分和非参数部分[18]，具有很高的拟合精度同时可以简化运算，提高计算效率。因此，采用Kriging方法来拟合屈曲载荷与各个参数之间的关系模型。

2.1 基于Kriging方法建立关系模型

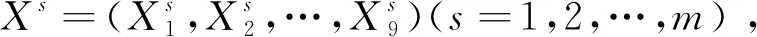
(2)

式(2)中：C=[C1(X),C2(X),…,C9(X)]T为多项式函数；β=[β1,β2,…,β9]T为回归系数；Z(X) 服从(0，δ2)的正态分布，其协方差为

Cov[Z(Xi),Z(Xj)]=δ2R(Xi,Xj)

(3)

式(3)中：δ为方差；R为m×m的相关矩阵，R(Xi,Xj) 为两个任意试验点Xi和Xj的相关函数，R选取Gaussian函数形式为

(4)

(5)

(6)

(7)

(8)

矩阵R可通过引入最小化函数来确定，进而求解出Kriging代理模型。

通过拉丁超立方采样抽取500个实验样本，随机挑选450组数据建立屈曲载荷与多个参数的Kriging的代理模型，将剩余的50组数据用于模型的精度检测，实际值与预测值结果如图3所示，最大相对误差为7.76%，预测的平均误差为3%。计算结果表明，使用Kriging建立的代理模型来预测复合材料加筋板的屈曲载荷是合理的。

图3 屈曲载荷实际值与预测值结果Fig.3 Actual versus predicted flexion load results

2.2 基于Sobol法的灵敏度分析

Sobol灵敏度分析法通常用于非线性、非单调的函数模型，能够便捷地计算出各输入参数对响应值的一阶、高阶以及全局灵敏度系数，它可以表示为多个子函数相互组合的函数，即

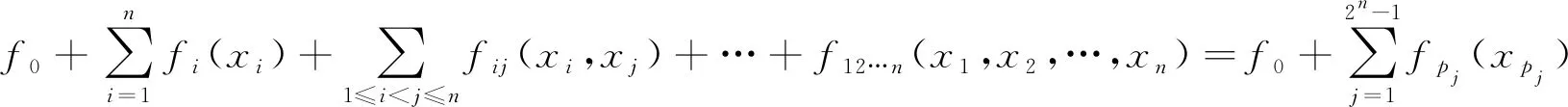
(9)

式(9)中：x=(x1,x2,…,xn)为自变量，定义域为Kn={(x1,x2,…,xn)|0≤xi≤1,i=1,2,…,n}；f0为常数；fpj为子函数表达形式，每个子函数间均为正交，且在其对应定义域内积分为0，即

(10)

因此，子函数的计算表达式为

(11)

式(11)中：dxi和dxij分别为dx1dx2…dxn中不含dxi和dxidxj的乘积；Kn-1为不含xi的定义域；Kn-2为不含xi和xj的定义域。

通过计算，可以求解出函数的每一项偏方差和总方差为

(12)

(13)

在Sobol的方法中，输入参数的灵敏度是由其对响应值总方差的贡献率进行评价的。因此，一阶响应指数Si和总一阶响应指数STi为

(14)

(15)

式中：Si为一阶灵敏度系数，反映了单一参数xi对复合材料加筋板屈曲载荷的影响程度；STi为全局灵敏度系数，反映综合考虑输入参数x1,x2,…,xn的变化情况时，各参数间交互作用对复合材料加筋板屈曲载荷的影响。

2.3 参数灵敏度分析结果

在得到Kriging代理模型Pcr(X)后，使用Sobol方法对复合材料加筋板的材料属性和几何参数进行灵敏度分析，分析流程如图4所示，分析结果如图5所示。

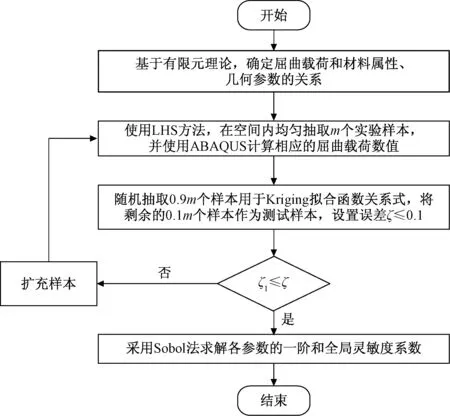
图4 复合材料加筋板参数灵敏度分析流程Fig.4 Parameter sensitivity analysis process for composite reinforced sheet

图5 复合材料加筋板参数灵敏度Fig.5 Parameter sensitivity of composite stiffened plates

复合材料加筋板的材料属性和几何参数对屈曲载荷的贡献量通常由全局灵敏度系数进行评价，由图5(b)可知，设计参数对屈曲载荷的全局灵敏度系数大小为ST6>ST8>ST5>ST1>ST9>ST2>ST4>ST3>ST7，X6与X8对应的一阶灵敏度系数与全局灵敏度系数相差较大，说明参数复合材料单层板厚度T和翼板宽度W之间相互交互作用最为明显。

根据图5的复合材料加筋板参数灵敏度计算结果，可以看出，复合材料加筋板的单层板厚度和翼板的宽度对响应值屈曲载荷的影响较大，其中，单层板厚度对屈曲载荷的影响最大，剩余几个变量的灵敏度数值较小，则表明这些参数对响应值的影响程度较小，因此，当设计目标为提高屈曲载荷时，应该重点关注复合材料加筋板的单层板厚度和翼板的宽度，尽量减少它们的随机不确定性。

3 结论

(1)在有限元分析的基础上，选取了9个变量为设计参数，基于Kriging方法的代理模型建立了屈曲载荷与材料属性、几何参数之间的函数表达式。

(2)运用Sobol灵敏度分析方法，对复合材料加筋板材料属性和几何参数进行灵敏度分析，结果显示单层板厚度和翼板宽度对屈曲载荷影响较大，则说明单层板厚度、翼板宽度为关键参数，为复合材料加筋板的结构设计提供指导。