克服阴影和车道线影响的路面坑洞识别研究

胡均平，邓穆坤，刘成沛

（中南大学 机电工程学院，长沙 410083）

0 引言

道路损坏是交通事故发生的一大诱因，这一情况引起了越来越多国家重视[1]。道路在使用过程中由于老化、车轮挤压、雨水冲刷、路基薄弱等原因容易产生裂缝、拥包、坑洞等各种道路损坏。路面坑洞是其中比较严重的一种道路损坏，不仅影响驾驶体验，也容易引发交通事故。如果车辆可以在驶入坑洞之前，识别出坑洞的存在，将能够为车辆的自动驾驶提供驾驶状态调整依据，从而提高驾驶的安全性。此外，实现对路面坑洞的自动识别也可为道路管理部门提供自动化道路质量检测手段[2]。

现有的路面坑洞识别方法主要有三种：基于振动的方法[3]、基于三维重建的方法[4]和基于二维图像的方法[5]。基于振动的方法主要是利用加速度传感器的梯度变化来识别坑洞，具有算法复杂度低的特点。但是这一方法的缺陷在于容易将减速带、拥包等误识为坑洞[1]。基于三维重建的方法，可分为三维激光雷达方法和立体视觉方法。采用三维激光雷达可以获得路面的很多细节信息，相对于其他的方法有着更好的效果，但是激光雷达成本昂贵[6]，采用立体视觉方法，需要匹配不同视角图像的特征点，算法时间花费较大。

基于二维图像的方法可以在低成本的情况下获得较好的结果，但是需要有好的算法去实现识别功能。Koch[5]等假设坑洞比周围路面亮度更低，利用三角阈值法分割坑洞非坑洞区域，几何特征椭圆率、面积等去除干扰区域，形态学细化和椭圆拟合法识别坑洞达到了86%的准确率。Ryu[8]等利用三角阈值方法将图像转换为二值图像，图像形态学和几何判据对坑洞区域进行提取，取得了73.5%的总体准确率。Wang[9]等提出了基于小波能量域和马尔科夫随机场的路面坑洞识别方法。Jo[10]等提出一种低花费的坑洞识别系统，Otsu阈值法二值化图像，取车道线之间区域作为感兴趣区域，利用纹理、几何特征提取坑洞区域，所提算法时间花费较低。Hoang[11]等利用方向可调滤波检测路面缺陷区域，积分投影得到形状特征后，利用监督学习模型对坑洞图像进行识别。

上述文献中的路面坑洞识别方法都取得了不错的识别结果，但是各种环境因素的干扰制约了识别精度的提升，阴影和车道线是其中两种常见的影响因素。为了克服阴影和车道线对路面坑洞识别的影响，本文对传统的灰度补偿算法模型进行了改进，将纹理和灰度信息融合到该算法模型中，并利用该算法模型在预处理步骤中对路面图像进行灰度补偿去除图像中的车道线和阴影。在得到灰度补偿图像后，利用小波变换和积分投影得到图像的形状特征，再结合支持向量机（Support Vector Machine，SVM）完成对路面坑洞图像的分类识别。在本文收集的数据集中进行的对比实验说明本文方法不易受车道线、阴影的影响。

1 克服阴影和车道线影响的路面坑洞识别方法研究

1.1 克服阴影和车道线影响的路面坑洞识别预处理

1.1.1 克服阴影和车道线影响的灰度补偿模型研究

路面图像中阴影区域因为光照被遮挡导致亮度较暗，车道线区域则因为色彩和材料的反射率的原因导致亮度较亮。因此阴影、车道线在灰度图像中主要表现为低灰度值和高灰度值块区，可以考虑通过灰度补偿去除。传统的灰度补偿模型可以较好地去除图片中的阴影，假设图片中阴影区域为B，非阴影区域为R，I（i，j）为灰度图像在（i，j）位置的灰度值，C为灰度补偿结果图像，AVGB、AVGR分别为阴影和非阴影区域的灰度均值，则灰度补偿模型如下[12]：

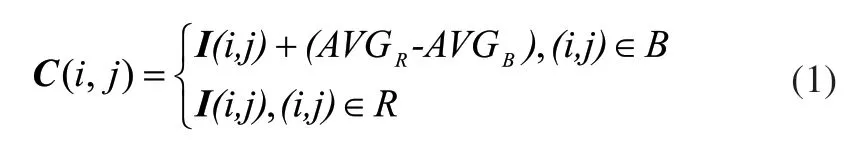
通常，路面坑洞边缘处会产生阴影导致原有的粗糙纹理丢失，坑洞和非坑洞区域差异变小，通过式(1)的灰度补偿并不能够提升坑洞边缘阴影区域纹理粗糙度，而且在存在车道线的路面图像中，采用这一补偿方法不能去除车道线。为了解决这个问题，本文对式(1)进行修正，得到下面可以克服阴影和车道线影响的灰度补偿模型：

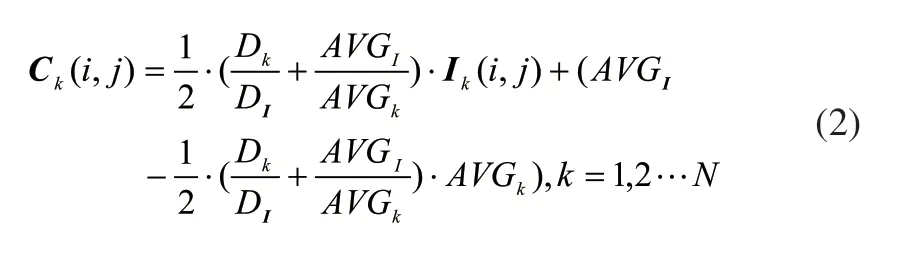
式中N是原始灰度图像按HSV色彩空间V通道分量进行按亮度分层分割后的层数，Ik（i，j）为得到的第k个分割灰度矩阵，Ck（i，j）为对应的照度补偿后的第k个分割灰度矩阵。Dk、DI和AVGk、AVGI分别为第k个分割灰度矩阵、整幅图像I的标准差和平均灰度值。在式(2)中用整幅图像的平均灰度值AVGI取代了式(1)中的非阴影区域平均灰度值AVGR，第k个分割灰度矩阵平均灰度值AVGk取代了阴影区域平均灰度值AVGB，这样通过式(2)图像中较亮和较暗区域都能够得到调整。标准差反映了图像区域的纹理粗糙程度，路面缺陷区域通常纹理更为粗糙，有着更大的标准差值，车道线区域纹理相对光滑标准差会相对较小，通过在式(2)中引入第k个分割灰度矩阵与整幅图像I的标准差比值，可以达到提升路面缺陷区域的纹理粗糙程度，降低非缺陷区域的纹理粗糙程度的目的，方便后续处理。观察发现，坑洞区域大部分情况下会在边缘处形成阴影，导致纹理粗糙度降低，将标准差比值引入并不能提升边缘处阴影区域的纹理粗糙度，为此本文在式(2)中加入了平均灰度比值。

1.1.2 克服阴影和车道线影响的灰度补偿算法步骤

1）提取V通道分量，HSV色彩空间完美的将亮度信息和色度分量分离[13]，为此将原始图像转换到HSV空间提取出V通道分量，并将V通道分量从[0，1]区间映射到[0，255]区间，同时原始图像灰度化得到灰度图像I。

2）对V通道分量进行高斯滤波，高斯滤波能够去除部分图像噪声，平滑掉图像阴影、车道线边缘，有利于后续的分层分割法分割操作更为精细，高斯滤波参数选择标准差为1.5，模板大小为9×9。

3）利用分层分割法进行分层分割，以V通道分量为基础，对图像进行分层亮度分割，设分层层数为N，阈值为P0，P1，Pk-1，Pk，…，PN，把属于阈值区间[Pk-1，Pk]的像素值置为1，其余像素值置为0，得到N个分割像素矩阵。再把这N个分割矩阵分别点乘第一步中得到的灰度图像I，得到N个分割灰度矩阵。对N个分割灰度矩阵，分别计算每一个分割灰度矩阵Ik（i，j）的标准差Dk和均值AVGk。同时计算原始灰度图像的标准差DI和均值AVGI。进过实验对比N取64较为合适。

4）灰度补偿，对N个分割灰度矩阵，按照式(2)进行灰度补偿，得到N个补偿后的灰度矩阵，再把这N个矩阵相加融合起来，得到车道线和阴影去除后的图像。

为了验证改进后灰度补偿算法的车道线、阴影去除效果以及纹理和灰度信息对去除效果的影响，在采集的数据集图像中进行了大量对比试验，图1是几种典型路面灰度补偿结果，图1(a)是原始图像，图1(b)是只融合纹理信息进行灰度补偿的结果图像，图1(c)是融合纹理和灰度信息进行灰度补偿的结果图像。对比图1(a)和图1(c)可以发现本文所提的改进的灰度补偿算法能够很好的去除路面图像中的车道线和阴影。对比图1(b)和图1(c)中的坑洞图像可以发现加入灰度信息可以弥补单独利用纹理信息的不足，提升图像中坑洞边缘低灰度值区域的纹理粗糙度。

1.2 小波变换提取路面图像缺陷区域

小波变换由于其优越的分析性能在很多领域都得到了运用，运用在图像处理上小波变换可以把图像像素点之间的变化转化为小波系数来表示，且能够进行多分辨率分析。路面图像中相对粗糙的纹理区域小波变换得到的系数幅值会大些，而相对一致的纹理区域得到的系数幅值会相对小些[14]。而本文分析的路面坑洞，坑内区域纹理会相对粗糙些，坑洞周围的健康路面纹理则会细致一些。即使坑洞内有积水，在坑洞的边缘还是会存在围绕坑洞的粗纹理存在。利用这一特性，就可以把路面的缺陷区域突出地表示出来。以图像的方式表示则是缺陷区域灰度值大表现为高亮区域。

图1 几种典型路面图像灰度补偿结果

图像经小波变换分解后可以得到四副子图像，分别是近似子图、对角细节子图（HH）、水平细节子图（LH）、垂直细节子图（HL）。本文采用下述公式对垂直、水平、对角的三幅子图像进行融合得到我们需要的层内融合图：

式中HHk、HLk、LHk分别代表第k层分解得到的对角、垂直、水平方向的细节子图，Rk代表第k层融合图像，通过上式第k层小波分解得到的三个细节子图就被融合到了一起。融合后的图像大小随着分解层数的增大而变小。为了便于后续分析，把融合后的图像调整为原始图像大小进行分解层之间的融合。层与层之间的融合依据下式进行：

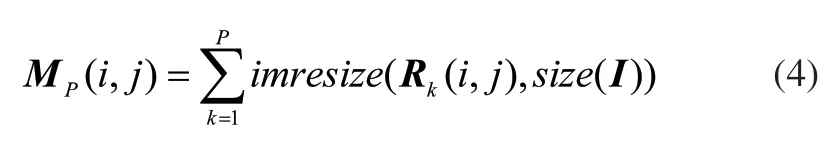
I为输入的灰度图像，MP（i，j）为小波分解后得到的前P层融合后的结果，对应系数值相加不再求均值，这样可以扩大噪声系数值和感兴趣纹理系数值之间的差异。上述小波变换中选择合适的小波基和分解融合层数是重要的，目前小波函数有很多，如迈耶小波（Meyer wavelet）、哈尔小波（Haar wavelet）、多贝西（Daubechies wavelet）等，经过实验对比多贝西小波对路面图像中的缺陷更为敏感，对周围健康路面噪声抑制地更好。

为了选择合适的分解融合层数，如图2小波变换分层融合图，1～3行分别为图1(c)中从左至右坑洞、裂缝、健康路面图像不同分解层融合后的图像，图1(a)列是小波变换后1到2层融合后得到的图像，图1(b)列是小波变换后1到3层融合后得到的图像，图1(c)列是小波变换后1～4层融合后得到的图像，从图中可以看出随着融合的层数的增多，图像越来越模糊，一定程度的模糊有利于减少下文积分投影曲线波动增强特征的表达能力。但是同时也应该注意到，随着融合层数的增多图像中缺陷区域的细节得到增强的同时周围健康路面的纹理细节、高亮噪声点也得到增强，太多层数的融合缺陷区域和健康路面区域的对比反而减弱，不利于提高算法的适用性。为此，本文选用小波分解的第1～3层进行融合。

图2 小波变换分层融合图

1.3 积分投影提取缺陷区域形状特征

利用上面得到的小波变换1～3层融合图像，对其进行水平和垂直方向投影，得到积分投影曲线。积分投影在人脸识别方面用的比较多而且成功，虽然它的原理很简单，但是在一定情况下可以很好的描述图片的特征。水平和垂直积分投影可定义为[11]：

式中VP和HP分别代表垂直、水平积分投影，n代表在横坐标为x时纵坐标方向上的像素数，m代表在纵坐标为y时横坐标方向上的像素数。

图3为图2(b)列中三种典型路面的一至三层融合图像的积分投影曲线，第一列是原始积分投影的曲线图，第二列是经过每9个值分段平均后的曲线图。第一行是坑洞图像对应的积分投影曲线，可以看到水平和垂直投影都存在明显波峰。第二行是竖向裂缝图片对应的积分投影曲线，其在水平方向上存在一个波峰，垂直方向上相对平缓。第三行所用图像是正常的路面图像，它的积分投影曲线没有明显波峰，垂直和水平方向上的积分投影曲线都处于小范围波动状态，造成波动的原因主要是路面本身具有颗粒状纹理，加之受到雨水、碾压等影响表面粗糙程度不一致，在积分投影曲线中就表现为不规律的小波动。从三种典型的路面缺陷的积分投影曲线图可以看出每一种缺陷都有不一样的积分投影曲线特性，运用这一特性可以将路面图像分类成有坑洞和无坑洞图像。

为了提取出特征向量，作为SVM的输入，可以将水平和垂直积分投影曲线值连接在一起得到形状特征向量，这样的向量中特征数量较多，曲线波动也较大。为了减少特征的数量，提高运算的速度，减少积分投影曲线波动对识别的影响，在积分投影的水平和垂直曲线中进行分段平均减少特征个数。从图3(b)列中可以看出分段平均后积分投影曲线波动减少，不同缺陷的路面图像形状特征更为明显。在第二节中，将对比特征数目对分类效果的影响。

1.4 路面坑洞识别分类模型

利用拉格朗日乘数法以及满足KKT条件下的拉格朗日对偶性，对式(7)进行求解得到最优分类函数：

图3 积分投影曲线图

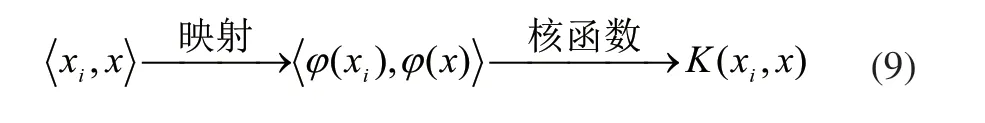
所以上面的式(8)可以改写成：

不同的核函数会产生不同的映射，分类效果也不一样，在后续实验中将探求核函数对分类效果的影响。

综上所述，通过本文提出的可克服阴影和车道线影响的灰度补偿算法预处理后的图像，结合小波变换和积分投影提取出形状特征后，利用SVM进行分类，即可实现克服阴影和车道线影响的路面坑洞识别。

2 路面坑洞图像识别实验及与其他方法的实验对比研究

2.1 坑洞与非坑洞路面图像SVM分类实验

实验算法在MATLAB2016a中实现，运行在Core i3 2.4GHz、4GB RAM的个人电脑上。实验所用的460幅图像来自于阴天、晴天、雨天等各种天气条件，也存在树阴、车道线、弱水渍、弱油渍的干扰。尽可能满足实际情况下的坑洞的状态，验证所提算法的实用性。

为了更好地反映支持向量机的分类性能排除随机性，样本分为坑洞、非坑洞图像两类，从两类中分层抽样取60%的样本作为训练集，余下的样本作为测试集，一共进行15次分层抽样，所有输入图像均规范至180×180像素，形状特征向量均进行归一化处理规范至[0，1]区间。采用交叉验证法把分层抽样所得的训练集分为训练和验证两个子集，对支持向量机进行训练和最优参数选择。为了客观地评价支持向量机的分类性能，对分类准确率（ACC）、精度（PRE）、真正率（TPR）[17]进行统计，同时计算接受者操作特性曲线（receiver operating characteristic curve，ROC）下的面积（AUC），AUC的值反映了分类器的分类能力。取上述4个指标15次测试的平均作为最后的性能评估结果。

支持向量机的核函数不同数据映射到高维空间的可分性不一样而产生不同的分类精度，为此，利用高斯、多项式立方、多项式平方、线性四种核函数对数据图像进行分类对比试验，支持向量机的参数采用贝叶斯优化算法进行优化。利用积分投影得到的形状特征最多可达360个数量较多，为了探求用较小的特征数达到好的分类结果，实验中分别取分段平均后120、90、72、60、40、36、30、24、18、12、10、8、6个特征进行试验。

试验结果如表1、图4所示，表1为不同核函数在不同特征数量下四个性能指标的均值，从表中可以看出立方核函数分类效果略佳，线性核分类效果最差。图4为立方核函数在不同特征数目时的性能表现，从图中可以看出特征数目大于10时分类性能趋于稳定，无需太多的形状特征数目，12个特征时可取得最好分类效果。此时坑洞识别分类准确率为87.4%，精度为88%，真正率为85.6%，AUC值为0.93。

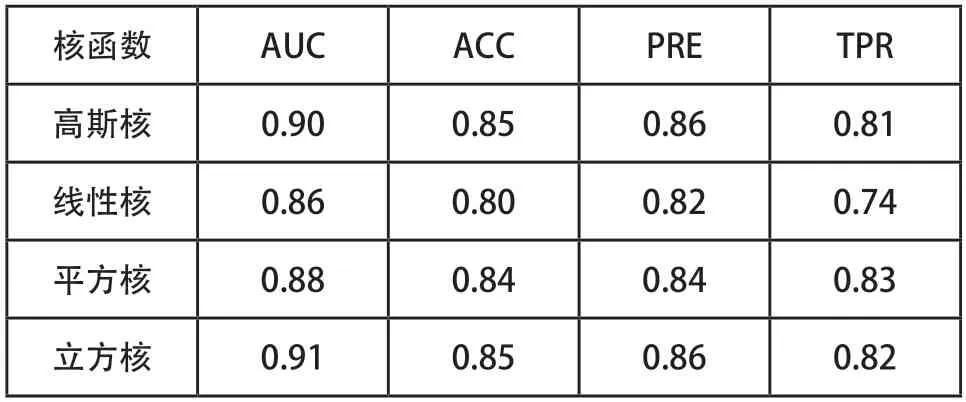
表1 不同核函数平均分类性能

图4 立方核函数分类性能

2.2 不同算法对比试验

为了验证本文算法的优势，将本文算法小波变换路面缺陷区域提取结果与基于直方图形状的三角阈值方法[5～8]，方向可调滤波方法[11]，小波能量域方法[9]的初步提取结果进行比较，结果如图5所示。

图5 不同算法效果对比

为了更好地识别路面坑洞，提取路面缺陷区域时，需要除去车道线、阴影等区域的干扰，即在提取的结果图中只有路面缺陷区域需要高亮显示，车道线、阴影等非缺陷区域是不需要也不能高亮显示的。从图5可以看出：三角阈值和方向可调滤波方法，在提取出路面缺陷区域的同时也将车道线、阴影区域提取出来，缺陷区域受到非缺陷区域干扰无疑会影响后续识别，如图5第1行中三角阈值方法结果图中阴影区域和坑洞区域同时高亮显示，这将使后续积分投影得到的形状特征不准确，最终导致支持向量机分类识别准确率降低；小波能量域方法相对于方向可调滤波和三角阈值方法对阴影、车道线的克服能力更强，但是它在图片中存在阴影的情况下，阴影区域被提取出来高亮显示，如图5第5行中小波能量域方法结果图中阴影区域高亮显示，比较而言本文方法则没有高亮显示阴影区域，避免了后续识别中将阴影误识为坑洞。另外，小波能量域方法在坑洞区域局部灰度值较高的情况下，坑洞区域提取不完整，如图5第2行中小波能量域方法结果图中坑洞区域右侧缺失，坑洞区域提取完整性欠佳，相比较而言，本文方法坑洞区域相对更为完整，这将提高后续形状特征提取的稳定性，进而提高支持向量机识别准确率。总的来说，本文方法由于进行了车道线、阴影去除预处理可以克服阴影、车道线对坑洞识别的影响，在高亮显示缺陷区域的同时不会将阴影、车道线等干扰区域也显示出来影响后续识别。

表2统计了利用文献[11]基于方向可调滤波的算法对本文所采集的数据进行坑洞图像分类识别的结果、文献[8]给出的结果，以及本文没有进行灰度补偿预处理得到的结果（Npours）和进行灰度补偿预处理得到的结果（Pours）。从表中可见由于本文算法进行了车道线、阴影去除预处理，路面坑洞图像识别效果更好。

表2 不同算法分类识别结果

3 结语

针对路面坑洞识别过程中易受阴影、车道线影响的问题，本文提出了一种灰度和纹理信息相结合的灰度补偿算法，并采用该算法对路面图像进行预处理，结果表明所提算法可以很好地去除路面图像中阴影和车道线，灰度和纹理信息的引入提升了缺陷区域的纹理粗糙度，使得经过小波变换分解与融合后提取的缺陷区域更为完整，提高了后续分类识别精度。利用支持向量机在包含460幅图像的数据集中对坑洞图像进行识别，立方核函数效果略佳，12个形状特征便可取得很好的分类效果，而特征数目的减少可以减少计算量。与现有算法对比，本文算法识别效果更优。