政府规制下废旧品正规与非正规回收群体的三方演化博弈研究

王建华 李富华

摘  要：针对当前资源浪费和环境污染問题日益凸显而废旧品回收机制不健全的现状，对市场正规和非正规回收群体的激励与制约机制进行探究，分析政府部门对两类回收群体策略选择的影响，构建政府部门、正规和非正规回收群体这三方演化博弈模型，利用数值仿真分析三个主体采取对应策略的演化趋势，以此判断政府部门采取不同策略时对于两类回收群体策略选择的影响。结果表明，影响系统演化至理想状态的因素包括政府部门对非正规回收群体转型升级的补贴、非正规回收群体转型升级策略时的收益、非正规回收群体从正规回收群体获得的技术溢出收益。

关键词：废旧品回收处理;三方演化博弈;演化稳定策略;数值仿真

中图分类号：F713.2    文献标识码：A

Abstract： In view of the increasingly prominent problems of resource waste and environmental pollution and the incomplete recycling mechanism of waste products， we will explore the incentive and restriction mechanism of the formal and informal recycling groups in the market， and analyze the influence of government departments on the strategic choices of the two types of recycling groups. The three-party evolutionary game model of government departments， formal and informal recycling groups uses numerical simulation to analyze the evolution trend of the corresponding strategies adopted by the three subjects， so as to judge the influence of the two types of recycling groups when the government departments adopt different strategies. The results show that the factors that affect the evolution of the system to the ideal state include government subsidies for the transformation and upgrading of informal recycling groups， the benefits of the transformation and upgrading strategies of informal recycling groups， the technology spillover benefits that informal recycling groups obtain from formal recycling groups.

Key words： waste recycling; tripartite evolutionary game; evolutionary stability strategy; numerical simulation

0  引  言

近年来，随着科学技术和经济的快速发展，产品的生命周期日益缩短，废旧产品越来越多，资源浪费和环境污染问题日益凸显。大量有用资源的浪费，加剧了我国资源短缺的矛盾。为实现废旧产品的循环再利用，降低资源消耗、减少废弃物排放，越来越多的国家和政府相继制定了更为严厉的环境保护政策和法律，可以说，作为解决由废旧品的环境污染和资源浪费问题的有效手段，对废旧品的回收问题已经受到社会各界的高度重视。目前，市场上对于废旧品的回收主要分为两种：一种是废旧品的正规回收群体;另一种则是废旧品的非正规回收群体。

将非正规与正规回收渠道一起考虑的主要有：余福茂等（2016）[1]围绕电子废弃物回收处理渠道的特点，综合考虑正规渠道的激励因素与非正规渠道的制约因素，建立回收处理渠道演化的系统动力学模型;谢天帅（2017）[2]建立了包括政府、正规和非正规回收者在内的两阶段动态三方博弈模型，研究电子废弃物非正规回收查处政策;夏西强等（2017）[3]为了分析政府不同政策对报废汽车回收渠道的影响，建立正规回收渠道与非正规回收渠道博弈模型;Huihui Liu等（2018）[4]研究正规部门和非正规部门之间的竞争，并构建拆除和整修过程的博弈模型;王文宾等（2020）[5]考虑政府给予正规回收商补贴以鼓励其回收更多废旧电子产品，研究补贴对双回收渠道价格竞争的引导问题，建立了正规和非正规回收商并存的双回收渠道回收价竞争模型探讨补贴对两种渠道的回收量、回收价和利润的影响。

只考虑非正规回收渠道的主要有：余福茂等（2016）[6]为探索在随机惩罚的情况下，政府监管策略和电子废弃物非正规回收群体回收行为之间的影响，构建了政府和非正规回收群体间的演化博弈模型;孙嘉楠等（2018）[7]为探究政府监管力度对废旧汽车非正规回收群体回收策略的影响，构建政府和废旧汽车非正规回收群体间的演化博弈模型;张金松等（2019）[8]认为非正规回收渠道的存在已经成为中国逆向供应链管理的一个严重问题，非正规回收商打破了废旧产品回收现有的正规模式。费威等（2020）[9]针对废弃食品非正规回收市场，非正规回收商数量导致单位回收收益随规模变化不同，分别建立了单位回收收益不变、增加与减少3种情况的非正规回收商预期总利润优化模型，分析了非正规回收商的伪装行动力与回收率决策，以及非正规回收商数量的影响效应。Fernanda Giffoni等（2020）[10]废物管理做法的可持续性是世界各地当局所面临的多方面挑战，尤其是在非正式部门起着重要作用的中低收入国家。结果表明，小型企业的效率很高，如果将其视为系统的一部分，则能够提高公共服务的可持续性。

政府的奖惩机制对回收群体的影响研究，王文賓等（2010）[11]基于政府的奖惩机制建立了4种情形下的博弈模型，结果表明，存在奖惩机制时废旧电子产品的回收率提高、回收商的利润增加及回收积极性提高;付小勇等（2012）[12]基于4种回收模式，建立逆向供应链回收演化博弈模型，得出政府补贴可以促使处理商选择直接回收方式的演化稳定策略，这有利于整个社会系统;徐兵等（2013）[13]基于政府补贴建立了政府、制造商和零售商的三阶段博弈模型，得出政府补贴能提高废旧产品的回收价格、回收量及各方的收益;王向等（2019）[14]从电子废弃品的回收模式，供应链参与主体间的合作机制以及政府补贴监管机制三个方面研究;朱庆华等（2019）[15]分析政府干预如何影响当前报废汽车市场的回收效率，分别建立了基于政府补贴、政府规范的博弈模型，并对比分析了补贴前后、规范前后正规回收拆解企业和非正规回收拆解企业的决策。

综上，现有研究已经认识到了废旧品回收的重要性，而且运用博弈模型分析废旧品回收的相关主体决策。但是对废旧品回收过程中，考虑到主体的有限理性，正规、非正规群体和政府部门的多方主体博弈关系分析有待深入，这三方主体的策略行为选择相关的重要。所以，本文基于演化博弈的理论，分析政府规制下废旧品正规、非正规回收群体和政府部门之间的三方演化博弈关系，更好的去分析这三个主体采取对应策略的演化趋势，以此去判断政府部门采取不同策略时对于两类回收群体的影响，从而得出相应的结论，为有效回收提供参考。

1  问题描述

对消费者而言，环保意识薄弱，以及丢弃或卖废品的便捷性，一般对于处理废旧品都很随意，基本上都是通过非正规回收群体进行回收处理，使得废旧品通过正规回收群体进行回收处理难度提升。对企业而言，要想提高回收量就必须提高废旧品的回收价格，让广大消费者尽可能去走正规回收渠道，这样的做法势必会使得正规回收群体加大投资去提升回收处理技术，但这种做法会大大提高正规回收群体的风险。根据当正规回收群体和非正规回收群体两方进行竞争时正规回收群体并没有什么太大优势，因此很有必要考虑政府部门的干预，本文构建政府部门、正规回收群体和非正规回收群体的三方演化博弈去对废旧品回收市场进行分析，探究更好的策略组合。

2  模型构建及参数设置

（1）假设1：行为策略，正规回收群体有“回收努力”和“回收不努力”两种策略;非正规回收群体有“转型升级”和“不转型升级”两种策略;政府部门有“监管”和“不监管”两种策略。“回收努力”即正规回收群体通过从其他地方引进新设备和技术人员来提升废旧品的回收效率，“回收不努力”表示正规回收群体保持原有的回收经营方式不做任何改变;“转型升级”即非正规回收群体通过转型，改变现有的回收方式，升级为正规回收群体，“不转型升级”表示非正规回收群体继续原有方式进行回收。政府部门有“监管”和“不监管”两种策略，当采取监管策略时，政府部门会对采取回收努力的正规回收群体和采取转型升级的非正规回收群体给予相应补贴;当采取不监管策略时，政府部门基本不采取什么相应措施。

（2）假设2：各个行为策略的概率，对于政府部门而言，采取“监管”策略的占比为X，则采取“不监管”策略的占比为1-X;对于正规回收群体而言，采取“回收努力”策略的群体占比为Y，则采取“维持现状”策略的群体占比为1-Y;对于非正规回收群体而言，采取“转型升级”策略的群体占比为Z，则采取“不转型升级”策略的群体占比为1-Z。

（3）假设3：参数设置，具体参数假设和基本解释如表1所示。

根据上述假设和设定，可以得出正规回收群体、非正规回收群体以及政府部门的博弈收益矩阵，如表2所示。

3  模型求解

3.1  复制动态方程

令政府部门采取“监管”策略时的收益为W，采取“不监管”策略时的收益为W，平均收益为，结合表2中的收益矩阵，政府部门采取“监管”和“不监管”策略的收益以及平均收益分别为：

W=Z*Y*-C+R-T-T+1-Y-C-C+F-T+1-Z*Y*-C-C-T+1-Y-C-C-C+F      （1）

W=Z*Y*R+1-Y-C+1-Z*Y*-C+1-Y-C-C                      （2）

=X*W+1-X*W                                            （3）

由演化博弈理论可知，上述政府部门策略的复制动态方程为：

=X*W-=X*1-X*F*Z*1-Y-Z2C+T-T*Y-C                        （4）

令正规回收群体采取“回收努力”策略时的收益为W，采取“回收不努力”策略时的收益为W，平均收益为，结合表2中的收益矩阵，正规回收群体采取“回收努力”和“回收不努力”策略的收益以及平均收益分别为：

W=X*Z*-C+R+T+1-Z-C+R+T+1-X*Z*-C+R+1-Z-C+R             （5）

W=X*Z*R-F+1-ZR-F+1-X*Z*R+1-Z*R                       （6）

=Y*W+1-Y*W                                          （7）

由演化博弈理论可知，上述正规回收群体策略的复制动态方程为：

=Y*W-=Y*1-Y*F+T*Z+T*1-Z*1-Y+Y*1-Y*R-R-C*Z+R-R-C*1-Z    （8）

令非正规回收群体采取“转型升级”策略时的收益为W，采取“不转型升级”策略时的收益为W，平均收益为，结合表2中的收益矩阵，非正规回收群体采取“转型升级”和“不转型升级”策略的收益以及平均收益分别为：

W=X*Y*-C+R+R+T+1-Y-C+R+T+1-X*Y*-C+R+R+1-Y-C+R         （9）

W=X*Y*R+1-Y*R+1-X*Y*R+1-Y*R                          （10）

=Z*W+1-Z*W                                          （11）

由演化博弈理論可知，上述非正规回收群体策略的复制动态方程为：

=Z*W-=Y*R+R+T-R-C+C+1-Y-C+R-R+T*Z*1-Z+X

+Y*R+R-C-R+1-Y*-C+R-R*Z*1-Z*1-X

3.2  均衡点稳定性分析

参考Selten的研究，在多群体演化博弈的动态复制系统中，演化稳定策略组合（ESS）是渐近稳定状态，渐近稳定状态必是演化稳定策略组合（ESS），在多群体演化博弈中，演化稳定策略组合（ESS）和渐近稳定状态都是纯策略纳什均衡。

由上述结论可知如果演化博弈均衡X是逐渐靠近稳定状态，则该均衡状态一定是纯策略纳什均衡，因此对于上述动态复制系统的研究只需要讨论如下0，0，0、1，0，0、0，1，0、0，0，1、1，1，0、1，0，1、0，1，1、1，1，1的渐近稳定性。判断各均衡点的稳定性可以用Jacobian矩阵局部分析法，如表3所示。

由表3各参数的实际意义可以看出1，1，0，1，1，1这两点至少有一个特征根为正，这样可以得出这两组的稳定性与参数的取值无关，且一定不稳定，而另外几个则与参数的取值息息相关。本文经研究认为当1，1，1不满足时，0，1，1则是较为理想的状态。下面在满足R

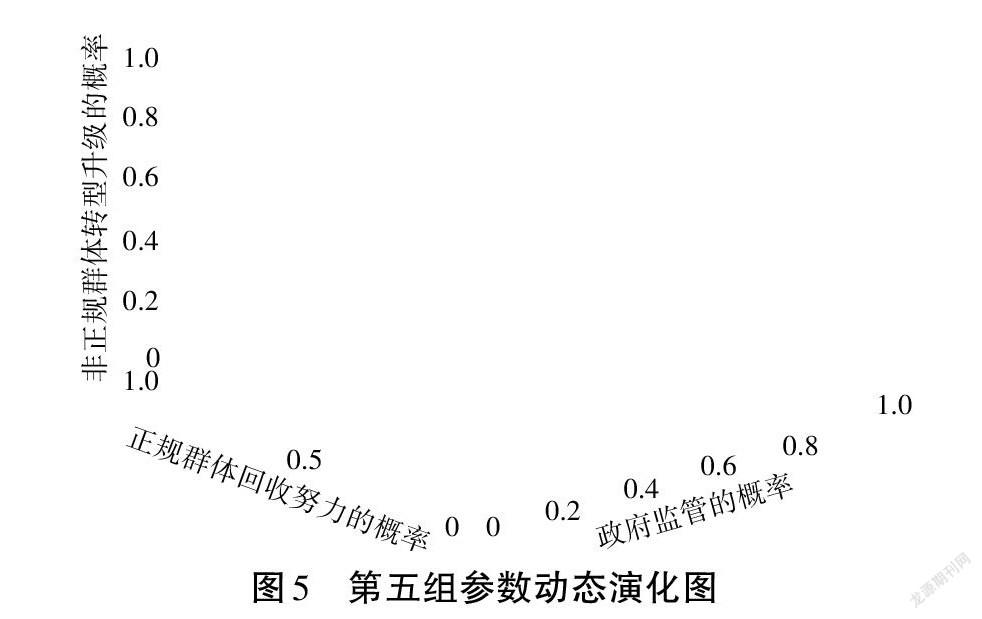
（1）当满足R

C=1，F=2。并带入上述矩阵可得出如下结论，各参数取值的特征根分别为1，3，-5、-1，-1，-4、-2，-3，4、0，1，5、2，1，-3、0，4，4、-3，-1，-4、3，-4，3。它们的判断结果分别为鞍点、ESS、鞍点、鞍点、鞍点、鞍点、ESS、鞍点。

由此可知，在第一组参数赋值中，演化稳定点为1，0，0和0，1，1。将第一组赋值带入三个主体的复制动态方程中可知，当初始条件满足时，系统最终会演化到1，0，0;当初始条件满足时，系统最终会演化到0，1，1并可计算得：满足最终演化为0，1，1的初始条件占比约为87%。本文通过大量随机取值方式来验证上述判断，并通过MATLAB软件得出从随机初始状态出发后的演化路径，如图1所示。

（2）当满足R

=3，R=1，R=5，R=1，C=1，C=1，C=1，F=2。并带入上述矩阵可得出如下结论，各参数取值的特征根分别为1，3，-5、-1，-1，-3、-2，-3，4、-1，1，5、2，1，-2、1，4，3、-4，-1，-4、4，-4，2。它们的判断结果分别为鞍点、ESS、鞍点、鞍点、鞍点、鞍点、ESS、鞍点。

由此可知，在第二组参数赋值中，演化稳定点为1，0，0和0，1，1。将第二组赋值带入三个主体的复制动态方程中可知，当初始条件满足时，系统最终会演化到1，0，0;当初始条件满足时，系统最终会演化到0，1，1并可计算得：满足最终演化为0，1，1的初始条件占比约为87%。本文通过大量随机取值方式来验证上述判断，并通过MATLAB软件得出从随机初始状态出发后的演化路径，如图2所示，通过计算演化点0，1，1的条件区域并对比图1和图2可发现第二组参数的收敛域较大。

（3）当满足R

=3，R=1，R=5，R=1，C=1，C=1，C=1，F=2。并带入上述矩阵可得出如下结论，各参数取值的特征根分别为1，3，-5、-1，-1，-2、-2，-3，4、-2，1，5、2，1，-1、2，4，2、-5，-1，-4、5，-4，1。它们的判断结果分别为鞍点、ESS、鞍点、鞍点、鞍点、鞍点、ESS、鞍点。

由此可知，在第三组参数赋值中，演化稳定点为1，0，0和0，1，1。将第一组赋值带入三个主体的复制动态方程中可知，当初始条件满足时，系统最终会演化到1，0，0;当初始条件满足时，系统最终会演化到0，1，1并可计算得：满足最终演化为0，1，1的初始条件占比约为87%。本文通过大量随机取值方式来验证上述判断，并通过MATLAB软件得出从随机初始状态出发后的演化路径，如图3所示，通过计算演化点0，1，1的条件区域并对比图2和图3可发现第三组参数的收敛域较大。

（4）当满足R

=3，R=2，R=5，R=1，C=1，C=1，C=1，F=2。并带入上述矩阵可得出如下结论，各参数取值的特征根分别为1，3，-4、-1，-1，-3、-2，-3，3、0，1，4、2，1，-2、0，4，3、-3，-1，-3、3，-4，2。它们的判断结果分别为鞍点、ESS、鞍点、鞍点、鞍点、鞍点、ESS、鞍点。

由此可知，在第四组参数赋值中，演化稳定点为1，0，0和0，1，1。将第一组赋值带入三个主体的复制动态方程中可知，当初始条件满足时，系统最终会演化到1，0，0;当初始条件满足时，系统最终会演化到0，1，1并可计算得：满足最终演化为0，1，1的初始条件占比约为87%。本文通过大量随机取值方式来验证上述判断，并通过MATLAB软件得出从随机初始状态出发后的演化路径，如图4所示，通过计算演化点0，1，1的条件区域并对比图3和图4可发现第四组参数的收敛域较大。

（5）当满足R

=3，R=3，R=5，R=1，C=1，C=1，C=1，F=2。并带入上述矩阵可得出如下结论，各参数取值的特征根分别为1，3，-3、-1，-1，-2、-2，-3，2、0，1，3、2，1，-1、0，4，2、-3，-1，-2、3，-4，1。它们的判断结果分别为鞍点、ESS、鞍点、鞍点、鞍点、鞍点、ESS、鞍点。

由此可知，在第五组参数赋值中，演化稳定点为1，0，0和0，1，1。将第一组赋值带入三个主体的复制动态方程中可知，当初始条件满足时，系统最终会演化到1，0，0;当初始条件满足时，系统最终会演化到0，1，1并可计算得：满足最终演化为0，1，1的初始条件占比约为87%。本文通过大量随机取值方式来验证上述判断，并通过MATLAB软件得出从随机初始状态出发后的演化路径，如图5所示，通过计算演化点0，1，1的条件区域并对比图4和图5可发现第五组参数的收敛域较大。

（6）当满足R

=3，R=1，R=5，R=3，C=1，C=1，C=1，F=2。并带入上述矩阵可得出如下结论，各参数取值的特征根分别为1，3，-5、-1，-1，-4、-2，-3，6、0，1，5、2，1，-1、0，4，4、-3，-1，-6、3，-4，1。它们的判断结果分别为鞍点、ESS、鞍点、鞍点、鞍点、鞍点、ESS、鞍点。

由此可知，在第六组参数赋值中，演化稳定点为1，0，0和0，1，1。将第一组赋值带入三个主体的复制动态方程中可知，当初始条件满足时，系统最终会演化到1，0，0;当初始条件满足时，系统最终会演化到0，1，1并可计算得：满足最终演化为0，1，1的初始条件占比约为87%。本文通过大量随机取值方式来验证上述判断，并通过MATLAB软件得出从随机初始状态出发后的演化路径，如图6所示，通过计算演化点0，1，1的条件区域并对比图5和图6可发现第6组参数的收敛域较大。

（7）当满足R

=3，R=1，R=5，R=4，C=1，C=1，C=1，F=2。并带入上述矩阵可得出如下结论，各参数取值的特征根分别为1，3，-5、-1，-1，-4、-2，-3，7、0，1，5、2，1，0、0，4，4、-3，-1，-7、3，-4，0。它们的判断结果分别为鞍点、ESS、鞍点、鞍点、鞍点、鞍点、ESS、鞍点。

由此可知，在第七组参数赋值中，演化稳定点为1，0，0和0，1，1。将第一组赋值带入三个主体的复制动态方程中可知，当初始条件满足时，系统最终会演化到1，0，0;当初始条件满足时，系统最终会演化到0，1，1并可计算得：满足最终演化为0，1，1的初始条件占比约为87%。本文通过大量随机取值方式来验证上述判断，并通过MATLAB软件得出从随机初始状态出发后的演化路径，如图7所示，通过计算演化点0，1，1的条件区域并对比图6和图7可发现第七组参数的收敛域较大。

4  结论与建议

本文考虑政府部门的干预，构建政府部门、正规和非正规回收群体三方演化博弈模型，探讨三方稳定演化策略组合，再利用MATLAB软件进行数值仿真分析结果，主要结论与建议如下：

（1）当满足R

（2）正规回收群体采取“回收努力”策略时的收益提高，会使得非正规回收群体从正规回收群体中获得的技术溢出收益提高，这样会更加促使正规与非正规回收群体分别采取“回收努力”与“转型升级”策略。

（3）政府部门对非正规回收群体采取转型升级时的补贴，非正规回收群体采取转型升级时获得的收益以及非正规回收群体从正规回收群体采取回收努力时获得的技术溢出收益这三个因素对系统演化到理想状态有很大影响。

（4）政府部门要对废旧品回收行业各个渠道商严格管控监管，才能有效地促进整个行业的规范化发展，为实现废旧产品的循环再利用，降低资源消耗、减少废弃物排放做出贡献。对废旧品回收的参与主体以及政府部门在策略选择上，应注重多种经营策略，可以思考进行技术合作，扩大企业规模，考虑相关税收政策。

参考文献：

[1] 余福茂，王聪颖，魏洁. 电子废弃物回收处理渠道演化的系统动力学仿真[J]. 生态经济，2016，32（6）：147-151.

[2] 谢天帅. 电子废弃物非正规回收查处政策及其效果[J]. 系统管理学报，2017，26（4）：722-727.

[3] 夏西强，朱庆华，王慧军. 政府不同策略下报废汽车正规与非正规回收渠道博弈模型[J]. 系统管理学报，2017，26（3）：583

-591.

[4]  Huihui Liu， Xiaolin Wu， Desheng Dou， et al. Determining Recycling Fees and Subsidies in China's WEEE Disposal Fund with Formal and Informal Sectors[J]. Sustainability， 2018，10（9）：174-177.

[5] 王文宾，丁军飞，林欣怡. 政府补贴对双回收渠道价格竞争的引导作用研究[J]. 科研管理，2020，41（3）：227-237.

[6] 余福茂，王希鹃. 随机惩罚下政府和非正规回收群体的演化博弈[J]. 杭州电子科技大学学报（社会科学版），2016（5）：1-6.

[7] 孙嘉楠，肖忠东. 政府规制下废旧汽车非正规回收渠道的演化博弈[J]. 北京理工大学学报（社会科学版），2018，20（5）：26-36.

[8] 张金松. 政府规制下的双渠道逆向供应链的治理机制[J]. 价值工程，2019，38（3）：74-76.

[9] 费威，唐浩. 废弃食品非正规回收商的决策分析[J]. 技术经济，2020，39（6）：165-174.

[10]  F F Luz， L Rozensk， M H？觔jek. Recycling capacity through formal and informal activities in six cities in So Paulo State， Brazil[J]. International Journal of Environment and Waste Management， 2020，27（2）：163-173.

[11] 王文宾，达庆利. 考虑政府引导的电子类产品逆向供应链奖惩机制设计[J]. 中国管理科学，2010，18（2）：62-67.

[12] 付小勇，朱庆华，窦一杰. 回收竞争的逆向供应链回收渠道的演化博弈分析[J]. 运筹与管理，2012（4）：41-51.

[13] 徐兵，杨金梅. 闭环供应链竞争下政府补贴效率研究[J]. 管理工程学报，2013，27（4）：178-185.

[14] 王向. 电子废弃品回收处理国内外研究综述[J]. 商讯，2019（33）：168-170.

[15] 朱庆华，李幻云. 基于政府干预的报废汽车回收博弈模型[J]. 运筹与管理，2019，28（10）：33-39.