LOCA范式下的课堂观察与教学改进

陈雪琴

摘要：运用LOCA范式，观察《相似三角形的判定》第三课时的教学。首先，观察学习历程，抽取关键事件：解决问题时，孤军奋战，缺乏沟通;公共分享时，听而不记，记而不思;知识应用中，简单模仿，缺乏深究。其次，分析关键事件，诊断学习问题：浅表学习无法实现知识的迁移;习惯性的浅表学习阻碍协同学习的开展;不善于反思就难以应对高挑战性问题。最后，针对学习问题，做出教学改进：营造学习环境，促进协同学习;转变教学理念，为学习而设计;搭建学习支架，发展高阶思维;调整教学节奏，留足反思时间。

关键词：学习历程;关键事件;课堂观察;教学改进;《相似三角形的判定》

焦点学生完整学习历程观察及关键事件分析法（Learningprocess Observation and Criticalincidents Analysis Approach，简称“LOCA范式”）作为一种课堂观察范式，实现了课堂研究方法的突破。它要求教师（观察员）在聽课时，选择一位或几位学生作为焦点学生进行观察与分析，观察收集焦点学生学习过程的完整证据并分析学习过程中的关键事件，在此基础上做出教学改进。本文以浙教版初中数学九年级上册《相似三角形的判定》第三课时的教学为例，探讨LOCA范式的运用。

一、观察学习历程，抽取关键事件

《相似三角形的判定》第三课时这节公开课设在学校录播教室，时长45分钟，学生四人一组面对面围坐在一起。在征得学生同意的前提下，我选择了梦瑶及其同组的俊芬、学乐、静文三位学生作为自己的观察对象。我（观察员）与四位学生的座位如图1所示。

课前，我与梦瑶简短交流。课上，我认真观察梦瑶和三位伙伴的学习历程，从中抽取记录关键事件。

（一）解决问题：孤军奋战，缺乏沟通

课始，教师先让学生回顾已经学过的相似三角形的判定方法：定义法;预备定理：平行于三角形一边的直线和其他两边相交所构成的三角形与原三角形相似;判定定理1：两角对应相等的两个三角形相似;判定定理2：两边对应成比例且夹角相等的两个三角形相似。然后引导学生类比全等三角形的判定方法猜想本节课的学习内容，即相似三角形其他可能的判定方法：三边对应成比例的两个三角形相似;一条直角边和斜边对应成比例的两个直角三角形相似。

在这三分多钟里，梦瑶有些紧张，没有回答教师的问题，也没有在学习单上写下回顾的内容。俊芬和学乐也存在类似的情况。静文则快速地在学习单上填好相似三角形的判定定理。其间，四位学生基本保持沉默状态，没有任何口头上的交流。

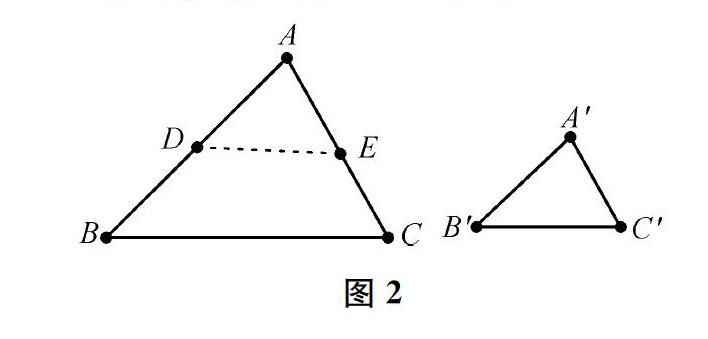
接着，教师让学生尝试证明三边对应成比例的两个三角形相似。梦瑶很快进入思考状态，画出△ABC和△A′B′C′后，添好辅助线DE∥BC（如图2），然后利用预备定理得出△ADE∽△ABC。这时，她发现问题没有她想的那么容易，因为她不知道如何证明△ADE≌△A′B′C′，但是，她仍然坚持独立思考，没有寻求同伴的合作。俊芬完全没有思路，只画了两个三角形就写不下去了，但是，她也没有说出自己的困惑，没有寻求同伴的帮助。学乐有了自己的解题思路及解题经验，但是没有跟同伴分享，也没有主动地向同伴伸出援手。静文因为忙于自己的解答，也没有时间与同伴交流。思考这个问题的整个过程中，四位学生没有任何交流，都在孤军奋战。

（二）公共分享：听而不记， 记而不思

大约八分钟后，教师让学生分享自己的学习成果。有三位学生主动举手发言，分享了三种不同的解法。

张同学的解法如下：

如图2，在线段AB上截取AD=A′B′，过点D作DE∥BC，交AC于点E，所以∠ADE=∠B，∠AED=∠C，所以△ADE∽△ABC，所以ADAB=AEAC=DEBC。

因为AD=A′B′，所以A′B′AB=AEAC=DEBC。又因为A′B′AB=A′C′AC=B′C′BC，所以AE=A′C′，DE=B′C′，所以△ADE≌△A′B′C′，所以△A′B′C′∽△ABC。

这里，其实直接用预备定理，由DE∥BC，即可证明△ADE∽△ABC，但是张同学还是绕了一下，通过两角对应相等来证明。

王同学的解法如下：

如图2，在线段AB上截取AD=A′B′，在线段AC上截取AE=A′C′，连接DE。

因为A′B′AB=A′C′AC=B′C′BC，所以ADAB=AEAC。又因为∠A=∠A，所以△ADE∽△ABC，所以ADAB=AEAC=DEBC，所以DE=B′C′，所以△ADE≌△A′B′C′，所以△A′B′C′∽△ABC。

对此，教师发现不少学生不能快速理解，就让王同学复述了一遍。

方同学首先作图：

如图3，延长BA、CA，作DE∥BC。

如此，显然无法准确作出平行线，于是，教师提醒方同学：DE的位置在哪儿？方同学更改作法：

延长BA至E，使AE=A′B′，延长CA至D，使AD=A′C′，作DE∥BC。

教师再次提醒作法不规范：点D、E确定后，直线DE已经确定了。方同学再次更改作法并继续解答：

延长BA至E，使AE=A′B′，过点E作DE∥BC，交CA的延长于点D，所以∠ADE=∠C，∠AED=∠B，所以△ADE∽△ABC。

此时，方同学的思路卡住了。教师简单地总结道：此解法与张同学的解法其实是类似的，只是所作的三角形位置不同，因为时间关系，课后再交流。

在这三位学生发言的过程中，梦瑶及小组的三位伙伴都放下笔，端坐倾听同学的讲解以及同学与老师的对话。梦瑶和俊芬在听的过程中，都没有记录发言同学的解题思路，更没有深度地思维加工。相比而言，学乐和静文在听的过程中，发现与自己不同的证明方法，会简单地记录下来，但也没有深入地思考总结。

由于时间关系，教师没有让学生修正、完善自己的解答，就直接布置了第二个学习任务：证明一条直角边和斜边对应成比例的两个直角三角形相似。并且只留了较短的时间给学生解答。梦瑶及小组同伴都只画了两个直角三角形，没来得及解答，更谈不上讨论。

在没有深入思考的情况下听发言同学和老师的分析，梦瑶、学乐、静文基本上能听懂，但是不一定能清晰、完整地表达;俊芬基本上处于迷惑状态，完全没有听懂。

（三）知识应用：简单模仿，缺乏深究

完成定理的证明后，教师让学生完成“运用1”：

如图4，添加一个条件，使得△ABC与△ADE相似。

梦瑶很轻松地写出了三个条件：（1）DE∥BC;（2）∠ADE=∠ABC;（3）ADAB=AEAC=DEBC。写好后，梦瑶看起来就比较自信了，开始跟俊芬轻声地分享自己的学习成果——这是这节课上她们唯一的一次组内交流。其实，对于这样两个有公共角的三角形，条件3可以弱化为ADAB=AEAC，但可能是因为这个条件是这节课新学的定理要求的条件，她就没有深入思考。

在随后的全班分享环节，有学生提出添加条件为ADAB=AEAC，但梦瑶依然没有反思，没有修正自己的答案。当发言的学生分享其他的方法，如∠AED=∠ACB、∠ADE=∠ACB、△ADE与△ABC都是等腰三角形等时，她还是只听不记，没有动笔完善自己的解答。

接着，教师让学生完成“运用2”：

如图5，O为△ABC内一点，A′、B′、C′分别是OA、OB、OC上的点，且OAOA′=OBOB′=OCOC′，求证：△A′B′C′∽△ABC。

梦瑶的解答如下：

因为OBOB′=OCOC′，所以△OB′C′∽△OBC。因为OAOA′=OCOC′，所以△OA′C′∽△OAC。因为OAOA′=OBOB′，所以△OA′B′∽△OAB。所以ABA′B′=BCB′C′=ACA′C′，所以△A′B′C′∽△ABC。

这里，她在证完三对三角形相似后，不知道如何进行下一步的证明，停留片刻后，写下ABA′B′=BCB′C′=ACA′C′，“完成”證明。

这时，差不多就到了全班分享的时间。教师将陈同学的解答投影到黑板上。他的解答跟梦瑶的几乎一样。教师提问：“证明△OB′C′∽△OBC运用的是相似三角形的哪个判定定理？”陈同学回答：“是两边对应成比例且夹角相等的两个三角形相似。”教师强调：“几何证明的书写一定要规范、严谨。另外，证明△OA′C′∽△OAC与△OA′B′∽△OAB时，因为方法类同，可以不重复书写，而写上‘同理，从而使解答更简洁。”接着，教师追问得出ABA′B′=BCB′C′=ACA′C′这一结论的缘由，陈同学经过努力，仍然无法准确表达。最后，由其他学生补充完成解答，教师再次强调推理一定要严谨。

此后，还有两位学生分享另外的两种证法。但是，直到下课，梦瑶都没有对自己的解答做任何修正。

二、分析关键事件，诊断学习问题

（一）浅表学习无法实现知识的迁移

证明三边对应成比例的两个三角形相似时，梦瑶很快添好辅助线DE∥BC， 利用预备定理证出△ADE∽△ABC，说明她对预备定理比较熟悉。但是，她不知道如何证明△ADE≌△A′B′C′，说明她对这道题的整体思路没有规划，思考问题只是抓住局部，不能全面考虑。她没有意识到，如果只是添加辅助线DE∥BC，虽然可以利用预备定理证明△ADE∽△ABC，但是这条平行线是不确定的，当然也就无法证明△ADE≌△A′B′C′。

尽管上课之前已经经历过两次整体思路和添加辅助线方法类似的证明，即两角对应相等的两个三角形相似的证明和两边对应成比例且夹角相等的两个三角形相似的证明，但是梦瑶在“第三次”证明时依然存在两个迷思：（1）添加平行线的目的有哪些？（2）如何利用已知的比例式A′B′AB=A′C′AC=B′C′BC和添加平行线后得到的比例式ADAB=AEAC=DEBC获得AD=A′B′、AE=A′C′、DE=B′C′？还需要什么条件？

从课堂反馈情况看，大部分学生在证明这个命题时都遭遇了类似的困境。这表明他们长期处于以机械记忆和模仿操练为主的浅表学习中，缺少深度思维加工，没有深入理解知识，难以在知识之间建立充分的联系，一旦问题情境稍加变化，就难以实现知识的迁移。即没有“融会贯通”，不能“活学活用”。

（二）习惯性的浅表学习阻碍协同学习的开展

浅表学习是一种以完成外在任务、避免惩罚为取向的学习行为。浅表学习的学生通常完全按照教师的指令行事，会端坐听课，但对自己不理解的地方不会深究;会认真记录教师要求记录的东西，但对其他个性化的、有价值的东西不会主动记录;会尝试完成教师布置的任务，但遇到具有挑战性的问题时，很少想尽办法解决，更多的是被动等待同学的分享及老师的讲解。

本节课中，笔者所观察的梦瑶和俊芬就有此特质：她们在学习陷入困境时，没有尝试不同的方法，也没有想到看教材、问同伴;在同学分享及老师讲解时，没有主动记录，更没有主动反思和修正。这样习惯性的浅表学习阻碍了同伴之间协同学习的开展。

学习共同体理念倡导的课堂变革以协同学习为核心。在与同伴相互探讨协作的过程中，学生会形成全身心投入、持续性探索的状态，主动思考、深化思维、克服困难、解决问题，不断反思和修正，最终从浅表学习走向深度学习。

（三）不善于反思就难以应对高挑战性问题

通过观察可以发现，梦瑶基本上能独立完成“运用1”，但是对综合性较强、挑战性更高的“运用2”就有点力不从心了。 完成“运用2”需要综合运用相似三角形的判定定理2、性质定理和判定定理3。从梦瑶的解答来看，首先，证明三对三角形相似时，她没有很好地理解判定定理2的条件，只呈现了两边对应成比例这个条件，没有呈现夹角相等这个条件;其次，证明三对三角形相似后，她没有想到性质定理，因而无法正确得到证明最终的三角形相似所需要的条件;最后，证明最终的三角形相似时，她只是联想到这节课所学的判定定理3，直接写出了所需要的条件ABA′B′=BCB′C′=ACA′C′，而没有深究这一条件为什么成立。此外，她也没有思考其他解法，更没有吸收他人的经验进行自我反思与修正。在解题过程中不善于反思已有思路，做出思路调整，就难以应对高挑战性问题。

三、针对学习问题，做出教学改进

（一）营造学习环境，促进协同学习

学习不是知识的被动接受，而是知识的主动建构;学习不能停留在自己的想法上，而是要通过交流获得提升。要让学生的学习真实地发生，就要让课堂处于安全、润泽的氛围中，让学生远离紧张、焦虑的心态。安全、润泽的学习环境，不仅能让学生坦然、自由地与同伴、教师分享自己的学习成果，而且能让学生开放、愉悦地接受同伴、教师的想法，从而通过合作提升学习品质。

为此，教师首先要做好“倾听”的示范，呈现“倾听”的身心状态，不仅用耳朵听，而且用心体会，诚心接纳学生的每一种观点，进而理解其背后的学习心理;其次要平等地对待每一位学生，尊重他们的个性差异，让乐于表达和羞于表达的学生都有表达的机会，让“懂”的学生充分地表达自己的见解，“不懂”的学生自如地说出自己的困惑;最后要组建和谐的学习小组，结合学生之间的人际关系，让学生自由地选择小组伙伴。

（二）转变教学理念，为学习而设计

设计教学时，教师通常从自己如何教的角度来考虑，而较少关注学生如何学。这导致教学设计往往脱离学生的学习需求。就本节课来说，因为添加辅助线的问题在前两节课中已经认真探讨过了，所以教师认为学生能够较好地完成添加辅助线的任务。但是实际上，在第一个定理证明的任务中，大多数学生不知道如何添加辅助线，导致完成任务出现困难。

美国著名教育心理学家奥苏伯尔有句名言：“影响学习的唯一重要的因素，就是学习者已经知道了什么。要探明这一点，并应据此进行教学。”因此，教师要改变教学观念，多关注学生的学，充分了解学情，了解学生的学习困难、“迷思概念”和“认知冲突”，了解学生学习的思维特点及认知逻辑，并以此为起点，为学生的进一步深度学习设计教学。

（三）搭建学习支架，发展高階思维

所谓“深度学习”，主要是指学习者能够自觉地运用高阶思维完成具有挑战性的学习任务。为了帮助学生完成具有挑战性的任务，教师需要搭建适宜的学习支架。就本节课来说，在第一个定理证明的任务中，学生最大的困难是不知道如何添加辅助线，没有意识到解决这个问题的核心是构造△ADE，使它既和△ABC相似，又和△A′B′C′全等，从而通过相似、全等的传递性来完成证明。因此，教师可以针对学生的这一学习困难，搭建如下学习支架：如何将△A′B′C′放大2倍、3倍等？在放大后的三角形上切一刀，你能切出与原三角形一样的三角形吗？切掉的三角形与放大后的三角形又有什么关系？写下你想到的所有方法及依据，然后与同组的伙伴分享，并记录同伴与你不同的想法。这样，在聚焦核心问题的基础上，把证明转化为操作，可以激发学生的学习动力，同时提示添加辅助线的方法。

（四）调整教学节奏，留足反思时间

“数学课程的内容不仅包括数学的一些现成结果，还要包括这些结果的形成过程。”要推进学生的深度学习，就要让教学节奏慢下来，留足反思、讨论的时间，让学生充分经历数学结果的形成过程。如果教师只顾完成教学进度，压缩学生反思、讨论的时间，那么，学生的学习就无法深入，更难以迁移。

就本节课来说，证明相似三角形的判定定理3时添加辅助线的方法与证明判定定理1和判定定理2时的方法基本相同。因此，教师应该在《相似三角形的判定》第一课时的教学中，给学生留足反思、讨论的时间，让学生修正、完善得到如下所有可能的添加辅助线方法：

1.如图2，在线段AB上截取AD=A′B′，过点D作DE∥BC，交AC于点;

2.如图2，在线段AB上截取AD=A′B′，作∠ADE=∠A′B′C′，交AC于点E;

3.如图2，在线段AB上截取AD=A′B′，作∠ADE=∠ABC，交AC于点E;

4.如图2，在线段AB上截取AD=A′B′，在线段AC上截取AE=A′C′，连接DE;

5.如图3，延长线段BA，使AD=A′B′，过点D作DE∥BC，交CA的延长线于点E;

6.如图3，延长线段BA，使AD=A′B′，作∠ADE=∠A′B′C′，交CA的延长线于点E;

7.如图3，延长线段BA，使AD=A′B′，作∠ADE=∠ABC，交CA的延长线于点E;

8.如图3，分别延长线段BA、CA，使AD=A′B′，AE=A′C′，连接DE;

9.如图6，延长线段A′B′，使A′D=AB，过点D点作DE∥B′C′，交A′C′的延长线于点E;

10.如图6，延长线段A′B′，使A′D=AB，作∠A′DE=∠A′B′C′，交A′C′的延长线于点E;

11.如图6，延长线段A′B′，使A′D=AB，作∠A′DE=∠ABC，交A′C′的延长线于点E;

12.如图6，分别延长线段A′B′、A′C′，使A′D=AB，A′E=AC，连接DE。

由此，在第二课时、第三课时的教学中，再碰到类似的添线情况，学生就不会手足无措，而是可以从容应对了。

参考文献：

[1] 陈静静.学习共同体：走向深度学习[M].上海：华东师范大学出版社，2020.

[2] 陈静静，谈杨.课堂的困境与变革：从浅表学习到深度学习——基于对中小学生真实学习历程的长期考察[J].教育发展研究，2018（13/14）.

[3] D.P.奥苏伯尔，等.教育心理学——认知观点[M].佘星南，宋钧，译.北京：人民教育出版社，1994.