壁温对压缩拐角流动影响的数值模拟研究

刘 亮，邱 波，曾 磊，姚 杰，朱目成

(1. 西南科技大学 制造科学与工程学院，绵阳 621010；2. 中国空气动力研究与发展中心，绵阳 621000)

0 引 言

高超声速飞行器气动布局中普遍存在一级或多级压缩拐角结构，如进气道、襟翼等。拐角区域存在分离再附流动、激波与边界层干扰等复杂现象，对局部热环境的分布会产生较大影响。针对这一结构，国内外学者进行了大量的研究。Davis和Sturvant[1]开展了非平衡真实气体对压缩拐角分离长度的研究。童福林[2]采用直接数值模拟（DNS）方法研究激波对边界层的影响，结果表明分离气泡上方的剪切层对分离流动有显著影响。Simeonides和Vermeulen[3]提供了二维压缩角中完全层流和过渡激波/附面层相互作用的实验数据，并对两个Navier-Stokes解算器进行了验证。John[4]研究表明前缘钝度会减小二维流场的分离区，增大轴对称流场的分离区。李素循[5]的研究表明楔面上的压力峰值随着楔角的增加迅速增大，且压力峰值的位置慢慢向楔面根部方向移动。陈苏宇[6]、赵一龙[7]对相关研究进行了总结和进一步研究，表明层流边界层在侧板激波作用下首先发生转捩，然后分离，分离后的流动为显著的半锥形流场结构，雷诺数对峰值热流大小和转捩过程影响明显。

总的来说，上述研究对于压缩拐角的流动特征已经有了较为全面的认识，但大多是在300 K均匀“冷壁”条件下进行的。而在真实的高超声速飞行中，气动加热会使得飞行器表面温度升高，壁面温度对于压缩拐角的影响显然不可忽略。

21世纪初，Marini[8]在压缩拐角的试验研究中考虑到了壁温比的变化。2006年，德国的Thomas和Herbert[9]针对双楔模型开展了风洞试验，选取了三种前缘钝度以及三种壁温进行研究，获取不同前缘钝度、不同壁温下的压力和热流数据。随后，Reinartz[10]等研究表明壁温会影响流动分离发生的位置。在此基础上，2014年，尚庆[11]等研究表明壁温会影响钝双楔转的转捩与流动分离，按第一级压缩面层流且第二级压缩面湍流进行数值模拟的结果能够在一定程度上与Thomas等的试验结果相符。Bleilebens和Olivier[12]采用可预热双楔模型进行实验研究，压力和热流测量的结果表明，主要影响因素不是壁面温度本身，而是壁温与自由来流温度的比值。2016年，代光月[13]对一薄壳状两级压缩楔进行了风洞试验研究，并采用多场耦合计算方法进行了验证分析，通过热壁修正公式将壁面温度作为流固耦合的中间边界条件。

上述研究让我们了解了壁面温度对压缩拐角影响的基本规律，但在温度变化范围、壁温对于流场结构的影响等方面仍有很多工作需要进一步深入，特别是在目前广泛使用的热壁修正公式的适用范围方面鲜有文献进行研究。针对该问题，在前人研究工作的基础上，本文选用文献[13]中的钝双楔模型并设计了多个计算工况，采用基于Navier-Stokes方程的自研程序进行数值模拟，在较大温度范围内分析了壁面温度对压缩拐角的流场结构、热流分布的影响。此外，本文使用热壁修正公式对无干扰区域和干扰区域的热流进行修正，通过与变壁温直接计算热流进行对比，初步分析了该公式对于压缩拐角流动的适用性。

1 数值计算方法简介

在笛卡尔坐标系下，守恒形式的三维非定常可压缩Navier-Stokes方程无量纲化后可写成如下形式：

其中，Re是无量纲雷诺数，Q是守恒状态变量，E、F、G是无黏通量向量，Ev、Fv、Gv是黏性通量向量。基于完全气体假设，取Sutherland公式所给出的黏性系数，普朗特数Pr= 0.72，空气的比热比γ= 1.4。

引入 计 算空 间 (ξ,η,ζ)， 使 其与 物 理空 间 (x,y,z)存在唯一的单值坐标变换，形式如下：

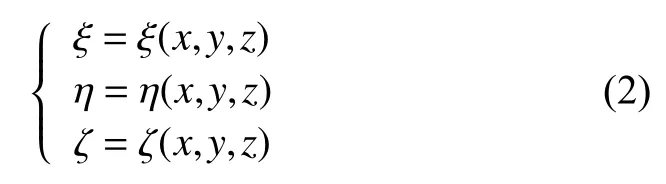
变换后Navier-Stokes方程可表述为：

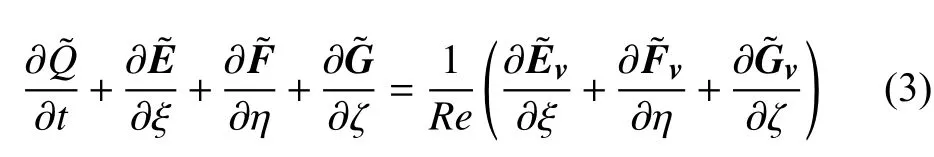
本文数值计算采取有限体积法，将上述方程转化为积分形式：

式中，f是封闭曲面S上的通量矢量，V是S包围的体积，n是S的单位法向向量。在网格线ξ、η、ζ包围的网格单元内对式（4）积分，可得半离散化方程，如式（5）所示：

式中，在ξ、η、ζ三个方向均采用Van Leer通量矢量分裂方法，以ξ方向为例：

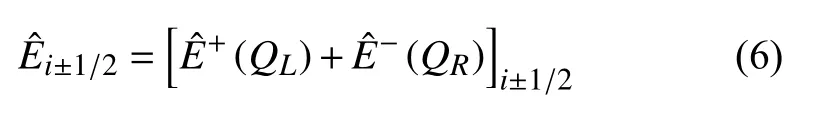
式中，采用MUSCL方法在交界面处插值，限制器取为Van Albada限制器。

对于高雷诺数的定常黏性流动，为了准确模拟边界层，物面附近必须使用很小的网格间距。为避免因显式格式时间步长过小所导致的收敛时间的大量花费[14-15]，本文中的定常Navier-Stokes方程采用Yoon提出的隐式LU-SGS方法。

湍流选用k-ωSST（Shear-Stress Transport）模型[16-17]，其控制方程为：

式中，k、ω分别代表湍动能和湍动能的比耗散率，μt为湍流涡黏性系数，β*为模型方程中相关常数，Φ为湍动能的产生项。

2 计算方法验证

为了验证本文计算方法对压缩拐角模拟的有效性，选用了Thomas和Herbert[9]的风洞试验模型和来流条件，对比分析中同时加入了Reinartz[10]和尚庆[11]对于该试验的计算结果。模型结构和尺寸如图1（a）所示；计算网格如图1（b）所示，第一层网格高度y+=0.002 mm，物面周向布点451个，物面法向布点91个；计算来流条件为Ma∞= 8.1，T∞= 106 K，Re∞= 3.8×106/m，p∞= 520 Pa；第一压缩面采用层流、第二压缩面采用湍流计算。

图1 Thomas和Herbert[9]风洞试验模型及网格Fig. 1 Thomas and Herbert[9] wind tunnel test model and Grids

本文计算流场结构与文献[9]试验纹影照片的对比如图2所示，分离点和再附点的位置、激波高度及激波角度的对比如表1所示。可以看到，虽然本文计算结果在激波高度和激波角与试验结果略有差异，但整体结构与试验结果吻合良好。

图2 压缩拐角分离区流场结构对比Fig. 2 Flow structure in separation zone of compression corner

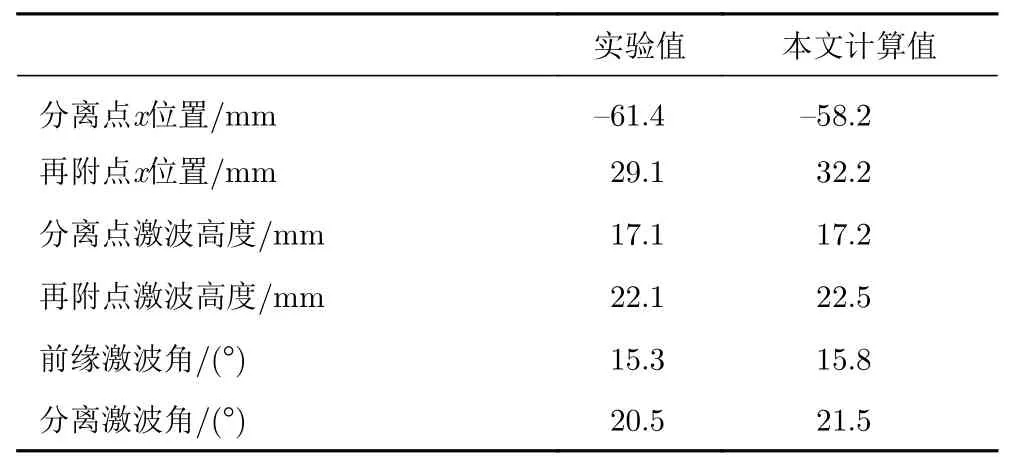
表1 与文献[9]流场参数对比Table 1 Validation of Flow Parameters with Ref. [9]

图3是迎风中心线上的压力系数对比结果，由该图可以看出，本文计算的压力系数与文献[10]和文献[11]数值计算结果对比良好，且与风洞试验结果的吻合度较高。

按公式将热流转换热流斯坦顿数St，再与文献[10, 11]进行对比，公式[18]表示为：

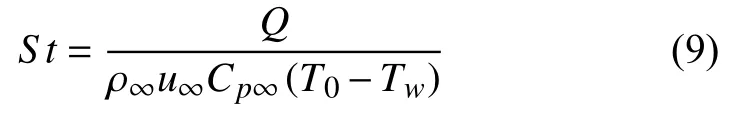
式中，Q为当地热流，Tw为当地壁面温度，T0为来流总温，Cp∞为 来流压力系数，ρ∞为 来流密度，u∞为来流速度。

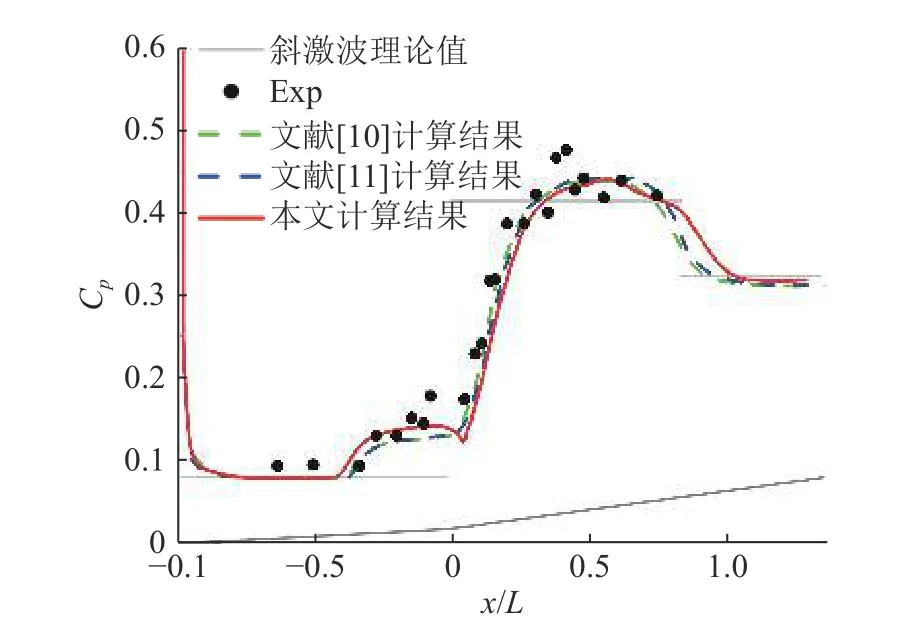
图3 压力系数对比验证Fig. 3 Validation of pressure coefficient distribution

迎风中心线的热流斯坦顿数结果如图4所示。由该图可以看出，本文计算的热流斯坦顿数与文献[10, 11]数值计算结果对比良好，但计算结果均比试验结果偏大，可能是由于第一压缩面采用层流、第二压缩面采用湍流模型，且不同计算方法对压缩拐角流动的数值模拟能力不同所导致的。

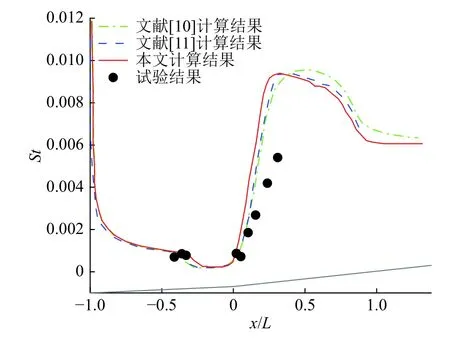
图4 直接数值模拟的热流斯坦顿数结果对比Fig. 4 Validation of St number of DNS results

综合本文计算结果与文献在流场结构、压力系数和热流斯坦顿数三方面的对比表现，可以看出本文所用计算方法对压缩拐角的数值模拟结果具有较高的可信度。

3 计算模型与工况条件

本文以文献[13]中的钝双楔形模型作为参考，取二维模型，模型包含两级压缩面，总长603.4 mm，前缘半径为3 mm，第一级压缩面水平长度445.93 mm,与下壁面夹角7.34°，第二级压缩面水平长度97.47 mm，与下壁面夹角25.52°，肩部长度60 mm，如图5所示。来流条件为：高度60 km、马赫数9、迎角-10°，壁温条件分别取300、500、700、900、1 100、1 300、1 500 K，来流温度T∞=247.021 K，则对壁温进行无量纲化（除以来流温度）可得壁温条件（Tw/T∞）分别为1.124 5、2.024、2.834、3.643、4.453、5.263、6.072。

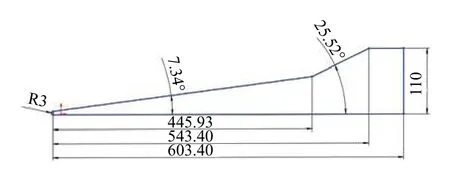
图5 计算模型(单位:mm)Fig. 5 DNS configuration (unit: mm)

计算网格如图6所示，第一层网格高度y+= 0.1 mm，物面周向布点581个，物面法向布点111个，网格雷诺数为8。在尽量保证网格尺度均匀、过渡光滑、物面正交性良好的基础上，在压缩拐角区域进行了适当的加密处理。

图6 计算网格Fig. 6 Computational grid

4 计算结果分析

4.1 壁面温度对分离涡结构的影响

高速来流经过压缩拐角处，由于逆压梯度的存在会形成分离涡，进而产生分离流动和再附流动[19]。壁面温度的变化会引起分离涡的变化，进而影响压缩拐角的热流分布[20]。

图7给出了分离点、再附点的具体变化情况，图8给出了部分壁温下干扰区的分离涡结构。可以看出，不同壁温下流场结果并未发生本质改变，但分离点、再附点的位置以及分离涡的大小发生了变化：随着壁面温度升高，壁温比增大，分离点向前移动、再附点向后移动，分离涡增大。分离涡增大。

图7 不同壁面温度下分离点、再附点位置Fig. 7 Separation and reattachment points at different wall temperatures

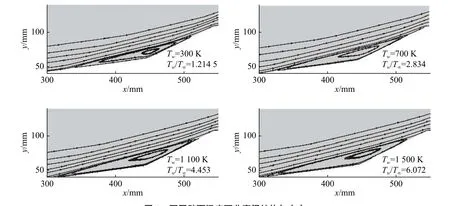
图8 不同壁面温度下分离涡结构与大小Fig. 8 Structure and size of separated vortices at different wall temperatures

图9是不同壁面温度下近壁面区域的气体密度、黏性系数、近壁面马赫数和压力变化图，通过对比可以看出：在高速来流条件下，壁面温度升高，壁温比增大，分离涡的整体流场结构基本不变，但近壁面区域的流体密度降低（图9（a））、黏性系数增大（图9（b））、速度边界层变厚（图9（c）），导致了逆压力梯度减小（图9（d）、图10），分离点向前移动、再附点向后移动，干扰区域增大。

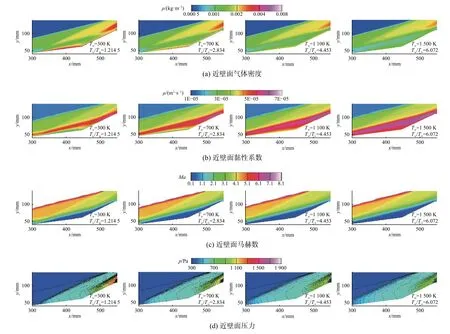
图9 不同壁面温度下近壁面气体密度、黏性系数、压力和马赫数变化图Fig. 9 Variation of near wall gas density, viscosity coefficient, pressure and Mach number at different wall temperatures

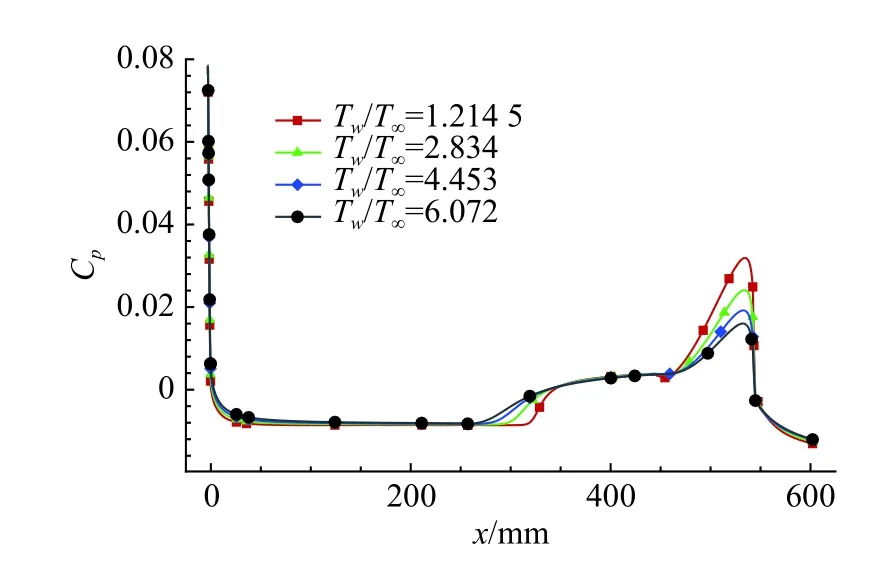
图10 不同壁面温度下的压力系数对比Fig. 10 Comparison of pressure coefficient under different wall temperature

4.2 壁面温度对热流的影响

迎风中心线的热流分布如图11所示,从图中可以看到：在分离点之前，热流沿着来流方向降低，同时随着壁面温度升高而降低；在分离点之后，热流出现了急剧的下降，且壁面温度越高，热流下降的越缓慢；在干扰区内，热流逐渐降至最低且在一段区域内基本保持不变；在第二级压缩面，热流开始逐渐增大。

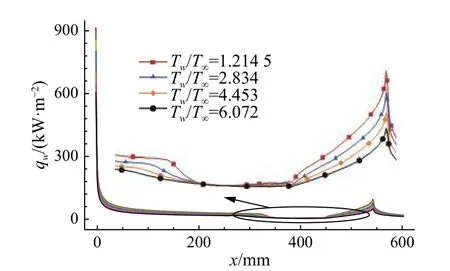
图11 迎风中心线热流密度分布Fig. 11 Heat flux distribution at windward centerline

统计不同壁面温度下分离点和再附点的热流，并以该壁面温度下的驻点热流为基准进行无量纲化处理，结果如图12所示。由图可知，随着壁面温度升高，壁温比增大，分离点无量纲热流增大，再附点无量纲热流减小。纲热流减小。

图12 不同壁面温度下分离点、再附点的无量纲热流Fig. 12 Dimensionless heat flux at separation and reattachment points at different wall temperatures

为了进一步量化壁面温度对压缩拐角不同位置热环境的影响，接下来分别取驻点、a点x= 150 mm、b点x= 315 mm、c点x= 360 mm、d点x= 480 mm、e点x= 541 mm等几个典型位置来分析热流的变化，如图13所示，其中a、e两点位于无干扰平板上，b、c、d三个点处于分离点和再附点之间的干扰区范围内。

图13 各位置取点示意图Fig. 13 Schematic of different points

统计这些点的热流，如表2所示。以各壁面温度下的驻点热流值为参考量将各个点的热流进行无量纲化处理，结果如图14所示。可以看到，驻点、a、b、d、e各点的热流均是随着壁面温度的升高而减小，其中b点热流减小的幅度最大，但c点的热流随着壁面温度的升高而逐渐增大。

由此可看出，对于本文计算的压缩拐角模型，在驻点和无干扰区域，热流随着壁面温度的升高而降低；在干扰区内，大部分区域的热流随着壁面温度升高而减小，且减小幅度比无干扰区更大，但在分离点与拐角之间的部分区域热流会随壁面温度的升高而增大，这主要是由于分离点前移、干扰区增大，该部分逐渐远离分离点所导致的。

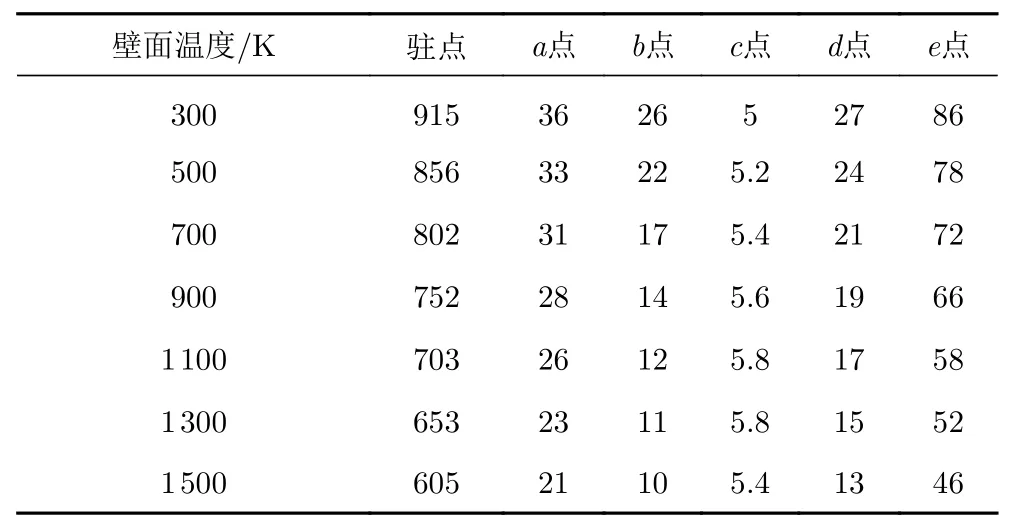
表2 不同壁面温度下各个点的热流密度值(单位: kW/m2)Table 2 Heat flux density at different wall temperatures (unit: kW/m2)

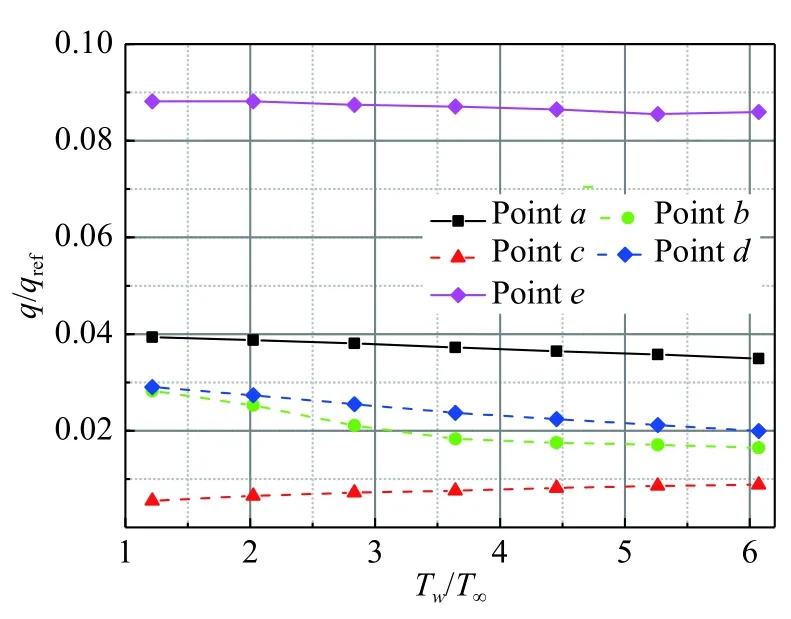
图14 几个典型位置无量纲热流随壁面温度变化Fig. 14 Dimensionless heat flux varies with wall temperature in several typical positions

4.3 热壁修正公式适用性分析

Chen等[21]基于高超声速边界层理论发展了一种高焓条件下热壁修正方法，该方法通过恢复焓和壁面焓对壁面热流进行修正，较大地简化了对边界层各物性参数的讨论，得到了广泛的应用。热壁修正公式可表示为[22-23]：

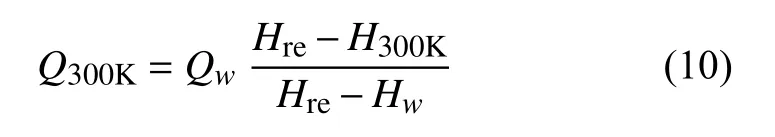
式中，Qw为当地壁面热流，Q300K为300 K条件下当地壁面热流，Hre为当地气流恢复焓，Hw为当地壁面焓，H300K为300 K条件下当地壁面焓。

恢复焓Hre表示为[18]：

转化为：

式中，He边界层外缘气流焓；r0是恢复因子，层流状态下取0.842 6，湍流状态下取0.892 1；ue是边界层外缘速度；普朗特数Pr≈0.71。

综合以上分析，人们对大量工程实践经验进行总结，将恢复焓表示为与总焓的一个关系式，如下所示：

式中，r为恢复焓系数，层流状态下一般取0.89，湍流状态下一般取0.92，H0为总焓。

这里利用公式（10）将表2中各点的高壁温热流修正到300 K壁温下的热流，前缘驻点热流及无干扰平板热流的修正结果如图15。由该图可以看出，修正后的热流与300 K的计算热流吻合较好，驻点最大修正误差在-1%以内，无干扰平板上a点和e点最大修正误差-5%左右，均在合理的范围之内。由此可见，对于本文所计算的压缩拐角模型，热壁修正公式对于前缘驻点和无干扰平板区域具有较好的修正作用。

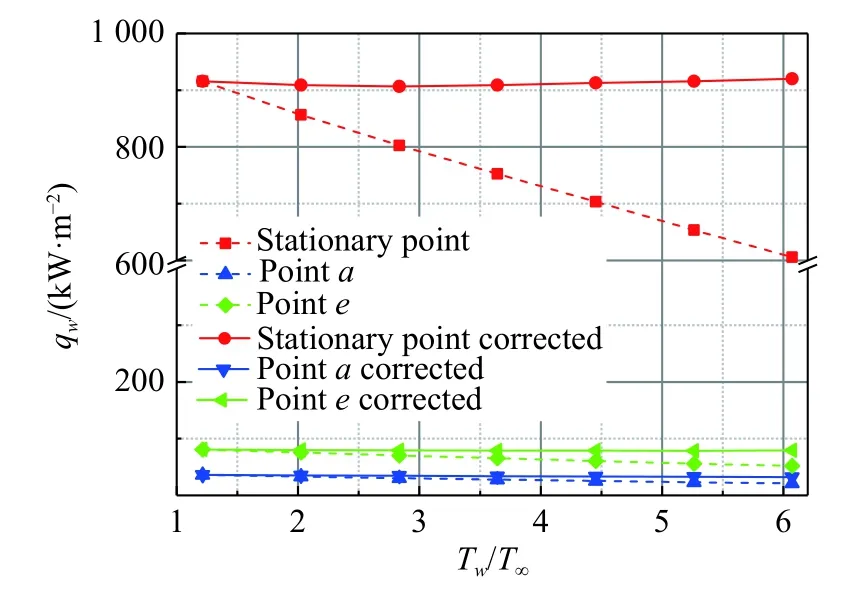
图15 驻点及平板上热流修正结果Fig. 15 Correction results of heat flux on stationary points and flat plates

干扰区热流的修正结果如图16所示，修正后b点最大误差-41%，d点最大误差-33%，c点最大误差60%。由此可见，热壁修正公式对干扰区的热流也具有一定程度的修正作用，但效果非常有限，导致修正结果与计算结果之间存在较大偏差。

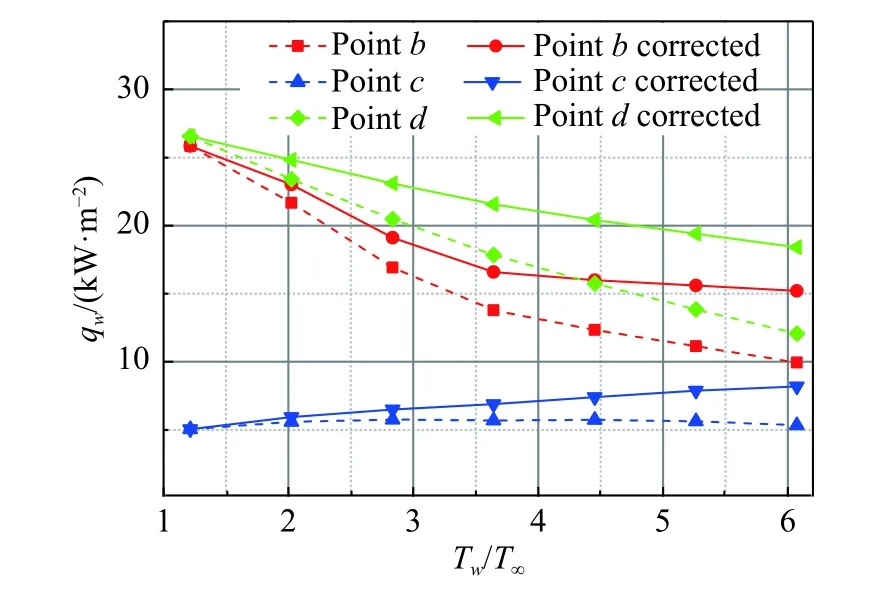
图16 干扰区热流修正结果Fig. 16 Correction results of heat flux in interference zone

综合来看，对于本文所计算的压缩拐角模型，其在圆柱前缘部分和无干扰平面区域较为适用，但其在拐角处干扰区的直接使用则存在修正精度降低、适用性不足的问题。

5 结 论

本文采用数值模拟的方法，在较大温度范围内(300 K～1 500 K)分析了壁温对高超声速压缩拐角流场结构和热流分布的影响规律，并探究了热壁修正公式在该结构上的适用性。针对本文所计算的压缩拐角模型，可以得出如下结论：

1）壁温升高，壁温比增大，近壁面区域的流体物性参数变化较大，导致逆压力梯度减小，拐角处分离涡增大。

2）压缩拐角大部分区域的热流随着壁温升高而减小，但热流并不完全遵循随壁温升高而减小的规律，在分离点与拐角之间的部分区域，热流会随壁温的升高而增大，这主要是由分离涡增大、分离点位置前移导致的。

3）热壁修正公式在圆柱前缘部分和无干扰平面区域较为适用，但其在拐角处干扰区则存在修正精度降低、适用性不足的问题。