基于三角模糊层次分析法的高原库区施工船舶安全预警系统的设计
李军 刘杰 杨梓辉


摘要:
为评估高原库区施工船舶安全并预警,构建基于三角模糊层次分析法的综合评价模型。运用三角模糊层次分析法确定各层指标权重,充分考虑各因素相对重要性比较中的模糊性。采用正态分布隶属函数确定最低层指标隶属度,运用模糊数学对专家评分进行模糊化处理,使得确定的隶属度更加真实可信,最终评价结果也更准确可靠。以此模型为基础设计基于VB.net语言的船舶安全预警系统软件,并用实例验证其科学性、合理性和实用性。
关键词:
施工船舶; 安全; 三角模糊层次分析法; 正态分布隶属函数; 预警系统; VB.net
中图分类号: U698.3
文献标志码: A
Design of safety early warning system for construction ships in plateau
reservoir area based on triangular fuzzy analytic hierarchy process
LI Jun1, LIU Jie2, YANG Zihui2
(1.School of Transportation Engineering, Wuhan Institute of Shipbuilding Technology, Wuhan 430050, China;
2.School of Energy and Power Engineering, Wuhan University of Technology, Wuhan 430063, China)
Abstract:
To evaluate the safety of construction ships in the plateau reservoir area and give early warnings, a comprehensive evaluation model based on the triangular fuzzy analytic hierarchy process is built. The weights of indicators on each level are determined by the triangular fuzzy analytic hierarchy process, where the fuzziness of relative importance comparison between factors is considered fully. The membership degrees of the bottom indicators are determined with the membership function of normal distribution, and expert scores are blurred by the fuzzy mathematics, which makes the determined degree of membership more authentic and credible, and the final evaluation results more accurate and reliable. Based on the model, the ship safety early warning system software is designed by VB.net language, and its scientificity, rationality and practicability are verified by examples.
Key words:
construction ship; safety; triangular fuzzy analytic hierarchy process; membership function of normal distribution; early warning system; VB.net
收稿日期: 2020-03-18
修回日期: 2020-07-30
基金項目: 青海省科技厅项目(2017-SF-138)
作者简介:
李军(1972—),男,湖北随州人,副教授,硕士,研究方向为交通运输安全、轮机管理,(E-mail)478036486@qq.com
0 引 言
青海省循化至隆务峡高速公路按照规划需要穿越高原黄河库区。该库区位于国家级风景名胜区内
,其两岸山崖陡峭、地形复杂。考虑到环保和成本两方面的因素,公路建设施工方决定采用船舶运输施工机械、废渣和建材,但是船舶运输潜在的安全风险给施工方和海事主管机关带来了严峻挑战,因此,有必要开发出针对施工船舶安全的预警系统。
目前有关船舶安全预警的研究主要有:熊兵等[1]以能见度为评判指标,以主管机关颁布的长江雾航规定为评判标准,创立了“二级预警、二级发布”的三峡雾情预警机制;GONG等[2]为减少船舶搁浅事故开发出搁浅预警模型,通过判断船舶模型领域内最小水深是否满足安全要求来实现船舶搁浅预警;张宝[3]运用层次分析法(analytic hierarchy process,AHP)探究了跨海客运渡船班线运营的安全状态和风险预警预控机制;姜丹[4]利用AHP和模糊综合评价法对复杂天气下三峡库区船舶安全进行评估,依据评估结果和海事部门相关规定确定船舶安全预警等级及评判标准;刘德林[5]综合运用AHP和模糊综合评价法,利用MATLAB建立了黑龙江流域船舶安全预警系统;吴兵等[6]为实现船舶撞桥前的安全预警及改进船舶过桥行为,提出一种基于模糊逻辑的船撞桥安全预警模型;陶阳[7]研究了连续桥区船舶过桥行为,分析船撞桥致因,建立了船撞桥模糊故障树预警模型;桑凌志等[8]为保障内河多桥梁水域通航安全,开发了实时可靠的内河多
桥梁水域船舶安全预警系统,该系统能实时检测出区域内高风险船舶并预警;ZHANG等[9]依据可拓理论,采用可拓工程方法建立多指标性能参数评价模型研究航运风险等级评价问题。综上可知,大部分学者在研究预警机理时综合运用AHP和模糊数学理论,但是研究的深度和广度还不够,实际操作也较困难。传统的AHP在比较两个因素的相对重要性时,认为结果只有一种情况,将一个具有不确定性、模糊性的比较过程绝对化。此外,在运用模糊数学理论时,大部分隶属函数的确定缺乏依据,与实际情况不符,并且定性因素较多,隶属度的确定也不客观。
针对上述问题,本文构建基于三角模糊AHP的多级综合评价模型。改进AHP,应用三角模糊AHP计算指标权重,体现因素比较过程中的模糊性,使得因素权重的确定更为科学、合理。将定性因素通过多位专家评分方式进行量化,运用正态分布的隶属函数插值计算隶属度,充分体现模糊性,使得确立的隶属度更为客观、合理。最后以此模型为基础开发基于VB.net语言的船舶安全预警系统软件。
1 施工船舶及作业环境风险分析
1.1 船型介绍
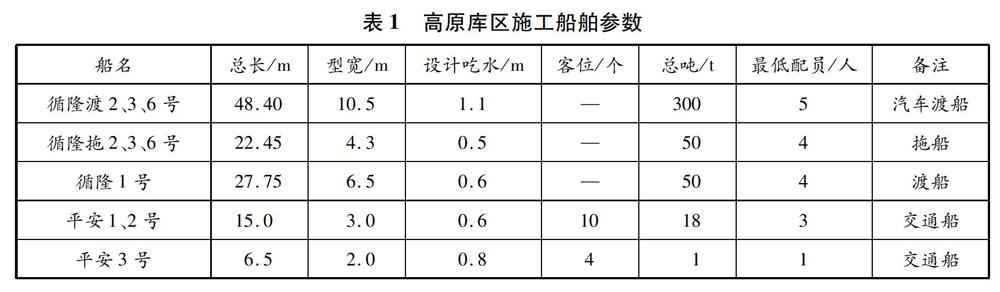
施工方为满足物资和人员的周转,先后投入3艘300总吨的汽车渡船,3艘50总吨的拖船,1艘50总吨的渡船,3艘交通船(其中2艘10人快艇,1艘1人应急快艇)。施工船舶具体参数见表1。除平安3号应急快艇采用汽油机驱动外,其他船舶均由柴油机驱动。
1.2 作业环境
(1)库区航道由天然航道改造而成,航道宽度范围为100~1 000 m,航道水深范围为30~130 m,航道弯曲河段较多,弯曲半径范围为700~5 000 m,目前高原库区航道被定位为B级航区6级航道。
(2)库区两岸属于典型的高山峡谷地貌。地形复杂多样,地势陡峭;库区内地层构造差异大,河流
两岸多断崖,易发生山体滑坡,在雨季尤其容易发生泥石流等灾害。
(3)库区地处青藏高原东北部,位于中纬度内陆高原,远离海洋,具有典型的大陆气候特征。查阅循化气象站气象资料可知,近7年库区最低气温为-19.8 ℃,最大风力为7级(能卷起0.9~1.0 m的巨浪)。
(4)库区水源为上游大坝泄洪和降雨,流向自西向东,流速3.02 m/s,年径流量约9亿m3。7月、9月强降雨易形成洪水,一次洪水过境约40 d,洪型矮胖,单峰型为主,峰、量匹配较好。在正常气候条件下,库区水位基本保持不變,水流缓慢;当库区有强降雨或大坝泄洪时,库区水位变化较快。为便于施工船舶装卸货物,对接施工场地,施工方沿高速公路施工线路在高原库区建了5个临时码头。
2 三角模糊AHP综合评价模型构建
2.1 评估指标体系设计
科学、有效的评价指标体系是预警系统发挥作用的重要前提,科学地甄别风险源是构建指标体系的关键。影响高原库区施工船舶安全的因素众多,在甄别风险源时既要充分考虑施工船舶所处的特殊环境,又要考虑施工船舶船员、当地海事管理机关和海事专家的意见。构建预警指标体系时,以“人-机-环境-管理”理论为基础,运用AHP搭建施工船舶安全风险评估三级指标体系,见表2。
该评估指标体系充分考虑了高原库区特殊的地理环境、恶劣的气象条件、宽窄不一的天然航道、复杂的通航秩序和人的因素对航行安全的影响。
2.2 评价集确定
采用五等级划分法对施工船舶的安全状况进行科学、合理的评价,用1、2、3、4、5分别代表安全、较安全、临界、较危险、危险。因此,确定的评价集为
z={z1,z2,z3,z4,z5}=
{1,2,3,4,5}。
2.3 评估指标权重的确定
传统的AHP是专家按照1~9标度法通过两两比较得到若干因素的相对重要性大小,然后构建判断矩阵,再运用运筹学的方法计算各因素权重。该方法仅仅考虑专家判断的两种极端情况,没有考虑专家判断的模糊性和主观性,导致评价结果的准确性有偏差[10]。为弥补AHP的不足,本文采用三角模糊AHP计算各因素权重,充分考虑专家对若干因素进行两两比较时的模糊性,用三角模糊数代替实数作为判断矩阵元素。三角模糊数自定义区间[l,u]能够反映专家判断的模糊性,区间越大专家对结果的判断越模糊,区间越小专家对结果的判断越清楚。[11-13]总之,三角模糊AHP充分考虑了专家对结果判断的模糊性,并且计算权重的过程较AHP更简单,不需要一致性检验。
2.3.1 三角模糊数基本理论
(1)三角模糊数定义。设M为实数域R上的一个模糊数,当M的隶属函数u(x)M(从
R到[0,1]
的连续映射)满足
u(x)M=x-lm-l,l≤x u-xu-m,m≤x≤u (1) 那么M就是一个三角模糊数,记为M=(l,m,u),其中l为下限值,m为中值,u为上限值。 (2)三角模糊数运算法则。两个三角模糊数Mi=(li,mi,ui)与Mj=(lj,mj,uj)的运算法则如下: 2.3.2 三角模糊AHP确定权重 (1)构建模糊判断矩阵。专家对某级的n个指标进行两两比较,并用三角模糊数表达比较结果,当专家给出n(n-l)/2个模糊判断后便构建模糊判断矩阵: 式中:i,j=1,2,…,n;aij=(lij,mij,uij),其中lij、mij和uij分别为三角模糊数的悲观值、可能值和乐观值。对于多个专家的判断结果,可以运用三角模糊数的运算法则取平均值作为综合三角模糊数。 (2)指标权重确定。根据三角模糊数定理一得 据此计算某级指标i的三角模糊数权重Di,再依据三角模糊数定理二得 计算Di≥Dj可能度,根据三角模糊数定理三得该级指标实数权重: 最后归一化处理后即可得到最终权重W。 2.4 建立评价指标隶属函数及确立隶属度 2.4.1 建立评价指标隶属函数的方法 模糊数学认為,当对某因素进行相对于评价集元素的评价时,其隶属度应该是[0,1],而不是绝对的“0”或者“1”。影响施工船舶安全风险的指标既有定性指标也有定量指标,对于定性指标需要分区间量化评价等级和定性指标,以便构建隶属函数。在评价定性指标时,首先划定各评价等级对应的评分区间,根据评分区间确立各等级区间隶属函数,然后由专家评分给出指标具体量化值,最后把量化值代入各区间隶属函数就可计算对应的隶属度。在此过程中,划分评价等级评分区间和确立隶属函数很关键,评价等级评分区间划分规则见表3。对于定量指标,采用专家调查法,经过多轮征询、充分反馈,获取指标的隶属度。鉴于专家的意见存在主观性和差异性,邀请海事院校、航运企业和海事主管机关等多个单位的专家,以确保评分过程的合理性和科学性。 2.4.2 正态分布隶属函数及参数的确立 由表3可知,专家评估某一指标时给出的量化值越靠近区间中点,指标隶属于该等级的程度越高,越靠近区间边缘,指标隶属于该等级的程度越低,甚至可能隶属其他等级。因此,选用正态分布函数为各区间隶属函数: 式中:x为专家对某一指标进行评价时给出的量化值;x0为各等级区间中点。显然,当专家给出的量化值为x0时,隶属度为1。当专家给出的量化值为区间端点时,模糊性最大,很难确定究竟隶属于哪个等级区间,对相邻两区间的隶属度分别为0.5,则有 式中:x1和x2为等级区间的两个端点。依据表3可知,x1-x2=20,由式(11)可求得参数σ=12.05。 2.4.3 正态分布隶属函数的修正 由第2.4.2节可知,正态分布隶属函数特点为:越靠近区间中点隶属度越高;越远离区间中点隶属度越低。但是两端区间例外,例如:[100,80)和(20,0]两个区间,越靠近100或者0两个端点隶属度越高,最高隶属度为1。因此,两端区间的隶属函数需要修正,对两端区间的隶属函数分别采取降低半梯度和抬升半梯度方法进行修正,使其变为平直的线段,使隶属度为1。修正后的各等级区间隶属函数如下: 由式(11)计算各等级区间隶属函数参数值,见表4。 综上可知,在专家给出某级某一指标的量化值后,可以依据式(12)~(16)计算出该指标隶属度,该级所有指标隶属度组成隶属度矩阵行R,本文仅计算三级指标隶属度矩阵行。 3 实例验证 3.1 计算各级指标权重 以三级指标“风、雨、雾、气温”为例阐述各级指标权重的计算过程。首先从海事主管部门、航运企业和海事院校各邀请一名专家,对该级指标进行判断,依据式(6)构建模糊判断矩阵,然后根据式(2)和(5)计算出综合模糊判断矩阵,见表5。 再根据式(7)计算该级指标三角模糊数权重,例如: 同理,DU112=(0.16,0.17,0.25),DU113=(0.41,0.43,0.60), DU114=(0.06,0.08,0.13)。 根据式(8)计算DU111≥DU11j(j=1,2,3,4)可能度, V(DU111≥DU111)=1,V(DU111≥DU112)=1,V(DU111≥DU113)=0.79,V(DU111≥DU114)=1。 根据式(9)计算U111实数权重dU111=min(1,1,0.79,1)=0.79,同理dU112=0.27,dU113=1,dU114=0.75。最后归一化处理后得到该级指标权重WU11= (0.28, 0.10,0.35,0.27)。其他各级指标权重也用上述方法计算。 3.2 确立三级指标隶属度 仍以三级指标“风、雨、雾、气温”为例阐述指标隶属度的确立方法。风、雨、气温为定量指标,可以从气象部门获取这3个指标的数据,并采用专家调查法经过反复征询确定其对各等级的隶属度;雾为 定性指标,由专家给出其量化值,然后应用式(12)~ (16)计算该指标对各等级的隶属度。例如,专家对雾给出的量化值为33,则其对等级4的隶属度为 同理可计算雾对其他等级的隶属度。对各指标隶属度归一化处理后构建隶属度矩阵行RU11,见表6。 3.3 模糊综合评价 求得三级指标“风、雨、雾、气温”的隶属度矩阵行RU11和权重WU11,选择合适的模糊算子即可求得评价结果SU11=WU11RU11,该评价结果也是二级指标“气象”的隶属度。同理求得其他二级指标的隶属度,组成隶属度矩阵行。运用三角模糊AHP求得二级指标权重,应用矩阵的乘法求得二级指标评价结果,该结果也是一级指标的隶属度。以此类推求得最终评价结果 SU=(0.19,0.05,0.16,0.28,0.32)。 按照隶属度最大化原则,可知最终评价结果中的最大值0.32对应评价集中“危险”项,说明在此条件下库区施工船舶处于危险状态,需要就近抛锚或者停靠码头。 4 施工船舶安全预警系统软件的设计与应用 4.1 预警系统软件设计 考虑到预警系统软件既可以在施工船舶上单机使用,也可以在施工方、海事局和施工船舶上联网使用,故采用单机和网络两种模式,在单机模式时采用Access 2003、SQL Server 2008版本以上数据库工具,在网络版本下采用SQL Server 2008版本及以上数据库,运用VB.net语言,选择微软公司的Visual Studio 2017开发工具平台在Window 10操作系统下完成系统软件的开发。依据预警系统担任的任务,设计由基础信息管理、评估体系管理、日常评估模块、评估数据管理、安全预警管理、系统管理等6个模块组成的预警系统,见图1。 4.2 预警系统应用 预警系统设计完成后,需要对系统的科学性、准确性和可行性进行检验。从当地气象部门采集库区气象数据,从地质部门获取库区地质灾害数据,从水利局获取库区水文数据,从海事局获取航道数据,通过雷达获取施工船舶航行状态指标数据,见表7。 运行高原库区施工船舶安全風险预警系统,得到的安全预警结论为“危险”,与实例验证的结果一致,证明了该预警系统软件设计的科学性和合理性。分析其原因发现:“雾”使得能见度不良,驾驶员无法看清航道航标,不能提前规避周围碍航物,可能导致碰撞、搁浅等海事事故;驾驶员已经连续驾驶8 h以上,身心俱疲,应急处理能力变差,也会导致海事事故;“经常性缺检”表明船舶维护管理不良, 这也是海事事故发生的原因之一。因此,综合评估 施工船舶处于危险状态符合此时实际情况。 5 结 论 施工船舶的安全状况不仅事关高速公路施工进程,还威胁人命、财产安全。高原库区自然环境恶劣、水文条件复杂、航道等级低等特点,决定了施工船舶安全风险因素的识别和评价工作的复杂性和特殊性。建立一套适合高原库区的施工船舶安全评价体系是进行船舶安全管理的基础。本文根据高原库区施工船舶的实际情况构建了施工船舶安全风险评估三级指标体系(包括4个一级指标、10个二级指标和23个三级指标)。该评估体系运用模糊层次分析法(AHP)计算各级指标权重,充分考虑了各因素相对重要性比较中的模糊性,使得判断矩阵的形成更加具有可操作性,权重的确立更加科学、合理。借助专家丰富的专业知识和实践经验对三级指标进行评分,并运用正态分布的隶属函数对评分进行模糊处理,使得隶属度的确立更加可信、符合实际,也使得评价结果更加准确。通过实例验证评估体系的科学性、合理性和实用性,以此评估体系为基础设计了基于VB.net语言的预警系统软件,解决了实用性难题。 参考文献: [1]熊兵, 张矢宇. 三峡雾航预警管理机制[J]. 水运管理, 2009, 31(9): 36-38. [2]GONGAnxiang, HU Qinyou, WANG Shengzheng. Vessel grounding warning with SAGA model[C]//PENG Qiyuan, WANG K C P, QIU Yanjun,et al. International Conference on Transportation Engineering 2007. ASCE, 2007: 512-517. [3]张宝. 跨海客运渡轮班线运输安全风险预警与防控研究[D]. 武汉: 武汉理工大学, 2016. [4]姜丹. 三峡库区复杂天气条件下船舶航行安全风险预警等级研究[D]. 武汉: 武汉理工大学, 2013. [5]刘德林. 黑龙江水域船舶航行安全评价研究[D]. 大连: 大连海事大学, 2014. [6]吴兵, 郭帆, 付姗姗, 等. 基于模糊逻辑的船撞桥风险预警方法[J]. 中国航海, 2019, 42(2): 47-51. [7]陶阳. 考虑船舶行为的桥区水域船桥触碰预警方法研究[D]. 武汉: 武汉理工大学, 2018. [8]桑凌志, 毛喆, 张文娟, 等. 内河多桥梁水域船舶安全航行预警系统实现[J]. 中国航海, 2014, 37(4): 34-29. [9]ZHANGYu, WANG Bo, TAN Zhendong. Research on the method of shipping risk early-warning based on matter-element-theory[J]. Journal of Shanghai Jiaotong University, 2011, 16(2): 252-256. DOI: 10.1007/s12204-011-1132-5. [10]陈曦, 曾亚武, 刘伟. 基于模糊层次分析法的农村水库大坝安全二级模糊综合评价[J]. 水利水电技术, 2019, 50(2): 168-176. DOI: 10.13928/j.cnki.wrahe.2019.02.024. [11]初良勇, 邵登华. 基于三角模糊数AHP的厦门港引航风险评价[J]. 上海海事大学学报, 2019, 40(4): 61-65. DOI: 10.13340 /j. jsmu.2019.04.011. [12]冯海斌, 郑绍钰, 曹立军, 等. 基于三角模糊层次分析法的装备基地级维修服务PPP采购合作伙伴遴选[J]. 装甲兵工程学院学报, 2018, 32(6): 33-40. DOI: 10.3969/j.issn.1672-1497.2018.06.006. [13]陈晨, 吴超仲. 基于三角模糊数层次分析法的驾驶人综合素质评估研究[J]. 武汉理工大学学报(交通科学与工程版), 2012, 36(3): 479-483. DOI: 10.3963/j.issn.2095-3844.2012.03.010. (编辑 贾裙平)

